基于能力提升的小学数学课堂习题设计探析

黄文毅

教师从实际生活中挖掘素材，以学生能力提升为目标，设计真实的情境，让学生在实践探究活动中解决问题，这样的课堂习题设计，有助于学生深化和巩固所学知识，也使学生在完成数学课堂练习的过程中，感受数学的魅力、发展数学能力、发展思维能力，提升学生的数学学科素养。本文就基于学生能力提升如何设计小学数学课堂习题，浅谈笔者的思考与做法。

一、设置互动性练习，培养自主探究能力

自主学习能力是培养学生终身学习和发展能力的基础，学生在课堂上的自主探究是落实“学生是教学主体”的主要形式。随着课程改革的深入，培养学生自主探究能力已成为课堂教学的重点之一。教师作为教学的组织者、引导者和合作者，要有意识地为学生创设自主探究的空间，适时适度放手，激发学生自主设计互动性练习的意识，可以起到意想不到的效果。

例如，教学人教版《义务教育教科书·数学》（下称“教材”）六年级上册《倒数的认识》一课时，当学生理解“乘积是1的两个数互为倒数”，“1的倒数是1，0没有倒数”，掌握了分子分母调换位置就可以求这个数的倒数时，对于大多数教师来说，教学任务已基本完成。此时教师还可以提问：“求倒数就这么简单，你还可以给你的学习小组提出什么有价值的问题？”学习小组进入相互提出问题、解答问题的状态，提出了多种类型的求倒数的练习，在小组中加以解决。

（1）求倒数

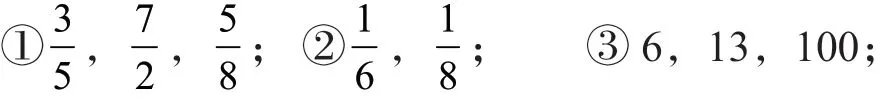
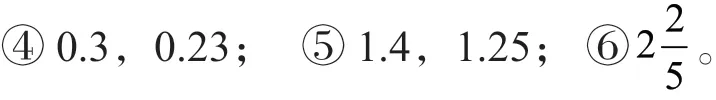
（2）将自然数的倒数在线段图上表示出来

学习“倒数”是学生学习分数乘法后，为学习分数除法所做的准备，学生通过相互提出问题，不断练习、加深认知，形成倒数的知识体系，从而进一步感悟了知识的内在联系和数学思想。

小学数学教学强调学生要用数学的眼光观察生活中的问题，以数学知识分析生活中的现象，并运用于实际问题的解决。教师要在准确理解教材意图的基础上，利用学生的生活经验，大胆寻找身边的数学问题，为学生架设“学”与“用”的桥梁，达到深刻理解数学知识和应用知识的目的。

例如，人教版教材四年级下册《乘法分配率》中，教材以学生植树作为初步学会乘法分配率的情境素材。当教完“挖坑的一共有多少人”（分配率）知识点后，学生的感觉仍然有些零乱茫然，究其原因，是学生生活经验的缺乏及图中信息量过度丰富，此时教师可以大胆放手让学生小组设计生活中的“分配率”真实性问题，并加以说理解决，如学校为球队购买多少套服装问题，图书馆添置一批阅览桌椅问题……在小组探究下，经过方法和说理的碰撞交流，学生进一步理解并掌握乘法分配率。这样贴近学生生活实际的探究活动，更符合学生的认知特点和心理特点，更利于学生对知识的理解，遵循学生的认知路径展开教学，消除了学习知识的障碍。

二、设置操作性练习，培养综合应用能力

操作性练习是提高学生解决实际问题能力和综合素养的有效途径。教师通过操作性实践活动能把抽象的数学知识具体化，通过改造教材练习题、操作探究和知识的迁移，让数学与学生的生活紧密联系在一起，达到拓宽知识、提高综合应用能力的目的。

例如，教学人教版教材二年级下册《近似数》时，学生利用线段图初步理解了近似数的意义。其中牵涉到近似数的精确度问题，可以精确到千位，也可以精确到百位，还有题目的数字比较特殊，精确到百位或十位结果都是同一个数，学生因此产生争论，此时，教师可以添加模拟数字，通过一题多图的操作训练，就可以实现三个层次的精确度，促进学生进一步理解近似数的意义。教师可以以例题的经验引导学生小组用线段图进行练习并求结论，如一台洗衣机的售价为3183元：

（1）姐姐说：洗衣机的价格约是（3000）元；

（2）妈妈说：洗衣机的价格约是（ 3200）元；

（3）爸爸说：洗衣机的价格约是（3180）元。

课后习题蕴藏着编写者的思想，这些现成材料为教学预留了足够的教学空间，教师可以从中筛选出有利用价值的题目，进行精心的习题设计，适时通过动手操作和必要的拓展训练，为学生提供更多的学习和发展的训练素材，从而发展学生的思维能力。

同一个问题多次激起思考的火花，数学知识深深植入学生的脑海中，更为重要的是学生获得了运用数学思想方法和思维方式解决问题的体验，提高了学生的综合应用能力。［1］

三、设置过程性习题，培养合情推理能力

推理是人们在学习和生活中使用的基本思维方式，它贯穿于整个数学学习过程中，是数学课程标准的十大核心概念之一。就推理能力而言，小学阶段主要发展学生的合情推理能力，即从已有的事实出发，凭借直觉和经验，通过类比和归纳等推断出一些结果，包括类比推理和归纳推理。在小学数学课堂习题设计中，探究过程再现试题，可以发展学生的合情推理能力。

例如，笔者设计了以下的计算试题：观察下列算式，并回答问题。

（1）根 据 以 上 的 规 律，计 算1011×1011-1010×1010的结果。

（2）根据以上的规律，请判断（A+B）×（A-B）和A×A-B×B的结果（ ）（填“相等”或“不相等”），你还能举出不同的例子来。

此题是用不完全归纳的方法学习平方差，是学生在学习加法交换律、结合律和乘法三个运算定律之后，在初步获得研究方法与研究结构的经验的基础上，通过对多个算式的观察，在归纳类比中获得数学猜想，并在运用中进一步寻求证据。教师设置这种过程性练习，让学生在练习中能运用数学语言，合乎逻辑地表达思考过程、有条理地进行讨论与质疑。此时练习已不再是抽象和枯燥的计算，而是探究过程的再练习、学习经验的再提升、研究方法的再创造，学生学习的热情高涨，思维的火花被点燃，合情推理能力得到提升。

四、设置说理性习题，培养正确思辨能力

思辨能力就是思考辨析能力，它是一种抽象思维能力，即条理清楚、层次分明的分析，清楚准确、明白有力的说理。在数学课堂练习设计中，教师可以适当设计一些说理试题，让学生层次分明，有条理、有理有据地说理表达，提升思辨能力。

例如，试题：书籍是人类的精神食粮，我国全民阅读量逐年增加。

（1）某学校积极响应国家号召，建议学生多读书，

小青经过对所在年级的5个班的调查，发现平均每个学生每学期读5本课外书，如果每班48个学生，照这样计算，全年级一学期共读多少本课外书？

（2）小青计划从8月15日到9月1日开学前看完一本190页的书，并计划每天看11页。你觉得她能做到吗？请说明理由，再提出合理的建议。

这样说理的习题设计，让学生追本溯源，层次分明、有条理、有理有据地进行说理表达，体会了数学知识的本质，培养了思辨能力，也推动了数学课堂教学向纵深发展。

五、设置开放性练习，培养学生的创新能力

教材的内容相对固化，教材中的例题、练习条件完整，问题固定、解法单一，答案呈现标准化，在面向全体学生的同时，也容易对教师的教学产生束缚，不利于满足学生成为发现者、研究者的强烈需求。从发展学生的应变能力和灵活思维能力的角度出发，应当加强设计开放性的课堂练习，通过开放性习题的探究性、发散性、发展性和创新性来吸引学生，激活其思路，利用各种思维途径和方法找到问题的最佳解法，促进思考和智力活动，培养学生的多变灵活的思维创新能力。

拓展性和开放性的课堂练习一般适合安排在每节课的末尾部分，学生在挑战性的练习解答过程中大彻大悟，牢固掌握数学知识技能，探索精神得到积极有效的激发。［2］因而有必要在每节课末尾都留下一定的时间开展这类练习。

1.开放性的课堂练习

传统教材面向全体学生，题目条件完整、结论唯一，题型相对固定封闭。开放性题目意味着条件、问题、解题方法的不固定，学生可以自己出题或互相出题，问题解答模式更加开放灵活，课堂教学得到了优化，个性思维充分发挥，综合运用知识的能力获得提高。

例如，在学校开展研学活动前，笔者设计了这样一道练习题：五年级组织全校860名学生去动物园参观研学，门票价格每人20元。按规定，人数满800人门票费可以享受团体9折优惠，人数满900人可以享受团体8折优惠，人数满1000人可以享受团体7折优惠。如果你是组织者，你打算怎样购买门票最合算？ 学生经过讨论计算得出结论：按1000人买票最合算。因为：860×20×0.9=15480（元），900×20×0.8=14400（元），1000×20×0.7=14000（元）。

通过非唯一的条件、问题，让学生能够用所学知识解决身边的问题，这样的题目对于学生来说是有吸引力的。更为可贵的是，部分学生接着提出了一个个有价值的问题，“是不是一定要按1000人的数量买最合算呢？”“哪种情况下按900人买，哪种情况下按800人买？”“按哪一种人数买，跟一张票的价格有关吗？”学生的思维再次被激起，不断的投入到新的探索中。为学生设计这样的开放性练习，对于激发学习积极性，增强应用意识，具有重要的现实意义。

2. 拓展性的课堂练习

拓展性练习是开发学生思维广度和深度的重要途径。对于学有余力的学生来说，在其他同学还没想出解答方法时，就通过自己独特创新的思维找到正确的解答方法，其对数学的学习兴趣更加浓厚。对于后进生来说，由于拓展性练习结合教学内容和目的要求，在常规练习中适度加深难度，他们仍然有能力参与思考、探究，也会从同学创新的解答方法中得到启发，使自己的能力水平得以发展。

例如，在教学教材四年级《路程、时间与速度》一课时，在学生基本掌握了路程、时间与速度的关系及应用后，教师设计了一个拓展性问题：

①苏炳添跑100米，用了10秒，他的速度是多少？是100÷10=10（米）吗？

②蜗牛爬行50米，用了5小时，蜗牛的速度是多少？是50÷5=10 （米）吗？

通过“难道苏炳添跑得跟蜗牛一样快？”的问题，在学生的疑惑中揭开复合单位涵义的知识面纱，这样的练习有趣、有启发性，体现了数学知识的神秘和魅力，学生的创新和实践能力得到充分提高，知识技能掌握得更加牢固。

基于能力提升的小学数学课堂习题设计，可以有效促进学生的数学学习，打开学生思维的窗扉，让学生的知识迁移能力得到发展，综合素养得到全面提高，灵活运用数学知识解决实际问题的能力得到进一步的提升。