靶场光电外测数据修正及弹道精确复现方法*

魏宗康，郭镇净，高荣荣

（北京航天控制仪器研究所·北京·100854）

0 引 言

外弹道测量及数据处理是导弹和航天器飞行试验工程的重要组成部分，它对于保障导弹、航天器试验的完成和促进其技术发展具有重要的作用[1]。随着导弹飞行试验的射程越来越远，测量精度的要求越来越高，由于光学经纬仪具有不受“黑障区”和地面杂波干扰影响等优点[2]，在导弹、运载火箭飞行试验的初始段和再入段测量中，光测设备现在仍是主要测量手段之一。但光电经纬仪存在测量距离较近和易受天气影响等缺点，需要与无线电测量设备相辅相成，共同完成飞行试验的测量任务。

为克服光电经纬仪测量距离较近的缺点，以获取更高精度的飞行轨迹，导弹试验靶场弹道测量设备的种类和数量不断增加。在雷达外测交接工作前，采用2台以上光电经纬仪分段测量导弹或者运载火箭的初始段飞行轨迹。但是，不同站点的测量设备在交接过程中引起弹道位置测量参数存在跳台阶的现象。为避免该误差，交接飞行段采取使用2台或2台以上光电经纬仪进行交汇定位的手段，通过不同设备之间的交叉检验识别某设备的野值数据，以提高弹道参数的估计精度[3]。

外测数据事后处理的结果主要用于评定导弹和运载火箭的性能和精度、分离制导系统工具误差等[4]。采用光学或无线电测量设备获取的飞行器弹道参数一般为位置数据，要想获得飞行器的速度和加速度，通常采用中心微分平滑方法及相应公式。但是，经过微分后得到的速度噪声过大，掩盖了初始段惯性导航的位置误差和速度误差。由于外测数据中含有随机误差，导致解算结果存在一定程度的波动，因此必须使用平滑滤波算法对解算结果进行处理，才能得到接近真实的飞行弹道参数[5]。常用的平滑滤波主要包含卡尔曼滤波[6]及多项式滤波[7-8]，但由于前者用于实时数据处理，要求精确的运动模型以及部分先验知识，有时在应用过程中无法满足该条件；而后者则用于事后处理，基于数据驱动建立参数回归模型，将数据处理问题转化为参数估计问题，以提高目标弹道参数精度[9]。常用的滤波算法有中值滤波和低通滤波等，其中应用最广泛的是卷积平滑算法[10]、样条插值算法[11]、小波分析[12]和经验模态分解（Empirical Mode Decomposition，EMD）[13]。但这些估计方法均未讨论其在平滑和滤波过程中对重要参数的设定准则，如何科学地设定算法的参数，使其获得最优的平滑与滤波效果，是一个有待研究的问题[14]。

因此，本文分析了不同站点的光电测量设备在交接过程中引起弹道位置偏差的原因，主要包括站址位置误差、时间不对齐误差和随机误差三大类，以及噪声过大带来的影响。并提出了一种多站交接点位置偏差分段修正的方法，以减小设备交接造成的位置误差和时间不对齐误差，再结合多项式拟合的方法降低噪声对速度的影响，从而得到连续平滑的弹道轨迹，实现弹道轨迹的精确复现。

1 光电经纬仪数据测量模型与误差产生分析

1.1 光电经纬仪测量模型

在靶场测试飞行器初始段弹道时，采用多站光电经纬仪分段接续测试的方式，各单站分别负责测量不同段的飞行轨迹。光电经纬仪是在光学经纬仪上加装激光测距系统构成。光学经纬仪为三轴（垂直轴、水平轴、视准轴）地平装置，水平轴和视准轴可以绕垂直轴在水平面内旋转，视准轴绕垂直轴旋转的角度由装在垂直轴上的码盘给出（相对某一基准方位），称为方位角；视准轴绕水平轴旋转的角度由装在水平轴上的码盘给出（水平面为零基准），称为俯仰角或高低角。

脉冲激光测距通过精确测量激光脉冲信号在测距系统与被测目标之间往返所需的时间来测定距离。由激光发射系统产生并发射峰值功率高、束散角小的激光脉冲，对主波脉冲和回波脉冲之间的时间进行精密测量，并换算成距离值输出。在主动段测量时，为了提高光电经纬仪的作用距离和测量精度，在导弹和运载火箭上经常安装激光合作目标[3,15]。

1.1.1 单站测量

图1 光电经纬仪单点测量示意图Fig.1 Schematic diagram of photoelectric theodolite single point measurement

采用单个光电经纬仪测量飞行器位置M的示意图如图1所示。图1中，OXYZ为发射坐标系，X轴朝向北，Z轴朝向东，O0点为光电经纬仪站址的位置，M点为导弹或者航天器的位置，则M点在发射坐标系中的投影分量为[15]

（1）

式中，R为光电经纬仪测量的导弹或者航天器相对站址的距离；E和A分别为光电经纬仪测量的高低角和方位角；x0、y0、z0为站址在发射坐标系中的位置分量；x、y、z为由光电经纬仪计算的导弹或航天器在发射坐标系中的位置分量。

1.1.2 多站测量

导弹或运载火箭发射起飞后，由2台以上光电经纬仪分段测量初始段的飞行轨迹（如图2所示）。图2中，采用了3台光电经纬仪，站址分别为O1（x01，y01，z01），O2（x02，y02，z02），O3（x03，y03，z03），分别负责OA段弹道、AB段弹道和BC段弹道的测量。

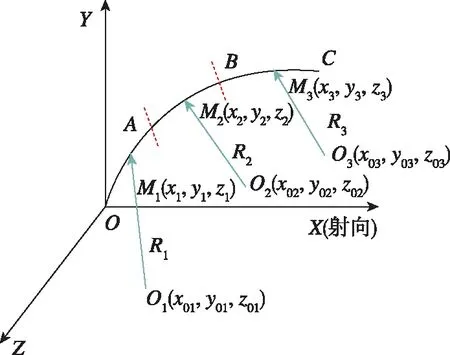
图2 光电经纬仪分段测量弹道示意图Fig.2 Schematic diagram of segmented ballistic measurement with photoelectric theodolite

当导弹或运载火箭在OABC段弹道飞行时，由这3台光电经纬仪分段接续进行测量。其中，OA段弹道中M1点、AB段弹道中M2点和BC段弹道中M3点的位置在发射坐标系OXYZ中的投影分量为

（2）

式中，i=1,2,3。

当得到OA段弹道、AB段弹道和BC段弹道的测量数据后，把三段数据按时间序列进行排列，即可得到弹道OABC段的弹道测量值。

1.2 光电经纬仪外测数据误差产生分析

采用多站测量方式时，会产生以下两个问题：

1）不同站点的测量设备在交接过程中，弹道位置测量参数存在跳台阶的现象。

采用3台光电经纬仪测量的导弹初始段弹道如图3所示，可以看出，测量数据分别在A点、B点交接过程中，弹道发生跳变。

图3 光电经纬仪分段测量的初始段弹道Fig.3 Initial trajectory measured by photoelectric theodolite

由于3个速度分量vx、vy、vz未发生突变，对三者分别积分后得到一组新的弹道位置数据x′、y′、z′，可得δx=x-x′、δy=y-y′、δz=z-z′，如图4所示。从图4中可以看出，δx和δz在发生跳变后其量值近似保持为常值，而δy的值会随时间单方向漂移。

图4 外测位置误差Fig.4 External measurement position error

根据式（2）得到位置误差方程为

（3）

其中，δ表示差值。

从式（3）可以看出，光电经纬仪外测误差可以归为三类：

①常值误差。主要为光电经纬仪的站址误差，在A点、B点交接过程中产生的位置误差主要是由站址O1、O2和O3的定位误差引起的。该误差为常值，可以补偿。

②时间不对齐误差。主要是由不同光电经纬仪之间的测量时间不同，以及对位置测量值进行微分时的时间延迟等。该项误差引起的位置误差与速度之间成正比，也可进行补偿。

③随机误差。该项误差主要是光电经纬仪的测角误差、激光测距仪的测距误差和测量数据的量化误差等，不可补偿。

2）速度噪声过大，掩盖了惯性导航的速度偏值。

对比图5中Z轴的z（蓝色曲线）和z′（红色曲线）可以看出，外测位置由于量化误差引起噪声偏大，其精度不能如实反映导弹的运动状态。

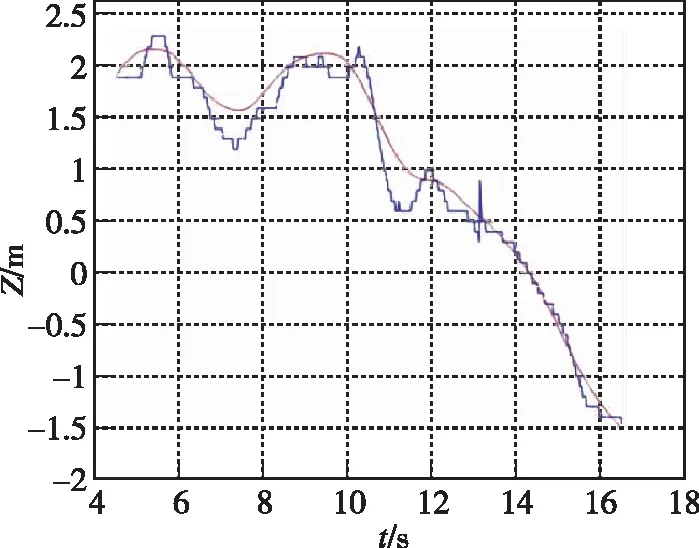
图5 外测位置与速度积分得到的位置对比Fig.5 Comparison between measured position and position obtained by velocity integration

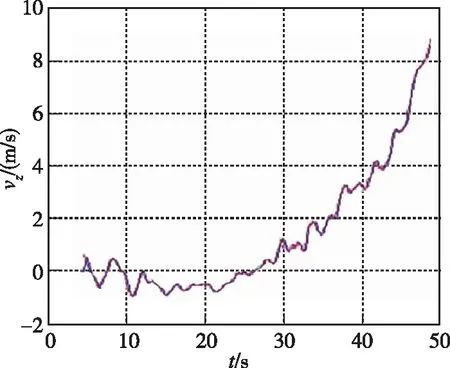
而用外测速度数据时，又面临着一个新问题，即噪声水平掩盖了惯性导航的速度偏值。图6所示为惯性导航的速度减去外测速度之后的速度差，该速度差的最大幅值接近1m/s。虽然惯性导航的速度误差会随时间而积累，但在该时间段的遥外测速度差远大于惯性导航的速度误差。因此，需要对外测速度进行平滑滤波，以能够如实反映惯性导航速度误差的变化趋势。

图6 惯性制导遥外测速度差Fig.6 Velocity difference of inertial guidance remote measurement

2 多站交接点位置偏差修正及外测弹道精确复现方法

为消除光电经纬仪的外测误差，本文提出了一种多站交接点位置偏差修正方法，旨在通过迭代消除均值差的方式，消除测量设备交接过程中产生的常值误差和时间不对齐误差，从而达到修正位置偏差的目的。并且给出了两种常用的去噪平滑的数据修正方法，以精确复现飞行器的弹道。

2.1 多站交接点位置偏差修正方法

对于由站点位置误差引起的光电外测跳变误差，本文针对可以补偿的常值位置误差和时间不对齐误差，提出了一种多站交接点位置偏差修正方法，通过分段迭代的手段消除均值差，从而修正位置偏差。具体算法流程如下：

（1）以第一个交接站点O2处前后的弹道OAB为例。首先，把OAB段弹道分为三段OA′、A′A、AB。假设该段弹道在A点跳变是由O2的定位误差引起，位置误差分量分别为δx02、δy02、δz02，三者为常值。以δx02为例，OAB段位置数据为[XOA′;XA′A;XAB]，位置误差为[δXOA′;δXA′A;δXAB]，速度数据为[vxOA′;vxA′A;vxAB]。XOA′和δXOA′分别为第一台光电经纬仪的测量值及其测量误差；XA′A和δXA′A分别为交接过程的测量值及其测量误差；XAB和δXAB为第二台光电经纬仪的测量值及其测量误差。

（2）其次，根据弹道中速度分量vx的数量级大小，考虑误差补偿类型。当速度数量级较小可以忽略不计时，进入步骤（2.1）；否则进入步骤（2.2）。

（2.1）当该段弹道中速度分量数量级可以忽略不计时，只考虑位置常值误差。

①首先，给定δx02的初值mx0。对δXAB统一减去mx0，可得数据集[δXOA′;δXA′A;δXAB-mx0]。分别计算δXOA′的均值为mx1，δXAB-mx0的均值为mx2，得到一组新的误差[δXOA′;δXA′A;δXAB-mx0-mx2+mx1]。其中，δx02=mx0+mx2-mx1。

②其次，给定δXA′A的初值nx0。对δXA′A统一减去nx0，可得数据集[δXOA′;δXA′A-nx0;δXAB-mx0-mx2+mx1]。计算δXA′A-nx0的均值为nx2，得到一组新的误差[δXOA′;δXA′A-nx0-nx2;δXAB-mx0-mx2+mx1]。

③最后，检验误差[δXOA′;δXA′A-nx0-nx2;δXAB-mx0-mx2+mx1]各段的均值。如果基本相同，得到修正后的外测值为[XOA′;XA′A-nx0-nx2;XAB-mx0-mx2+mx1]。一般情况下，经过上述计算后即可得到满足要求的结果。如果精度要求较高时，可采用迭代计算。

（2.2）当该段弹道中速度分量数量级不可忽略时，需要同时考虑站点位置误差和时间不对齐误差两部分。

①首先，根据下面的误差公式，以δXAB和vxAB测量值为例，采用最小二乘算法估计出位置偏差量δrx和时间不对齐误差量Δt。

δX=δrx+vxΔt

（4）

②其次，把交接设备前的速度数据vxOA′代入式（4），可得

（5）

由此，可求得

（6）

进而得到一组新的外测值[XOA′-vxOA′Δt-δrx;XA′A-vxA′AΔt-δrx;XAB-δx02-vxABΔt-δrx]。

③然后，仍需对δXA′A进行修正。给定δXA′A的初值nx0，对δXA′A统一减去nx0，可得数据集[XOA′-vxOA′Δt-δrx;XA′A-vxA′AΔt-δrx-nx0;XAB-δx02-vxABΔt-δrx]。计算δXOA′的均值为nx1，可得到一组新的误差为[δXOA′-vxOA′Δt-δrx;δXA′A-vxA′AΔt-δrx-nx0-nx1;δXAB-δx02-vxABΔt-δrx]。

④最后，检验误差[δXOA′-vxOA′Δt-δrx;δXA′A-vxA′AΔt-δrx-nx0-nx1;δXAB-δx02-vxABΔt-δrx]各段的均值。如果基本相同，得到修正后的外测值为[XOA′-vxOA′Δt-δrx;XA′A-vxA′AΔt-δrx-nx0-nx1;XAB-δx02-vxABΔt-δrx]。一般情况下，经上述计算后即可得到满足要求的结果。如果精度要求较高时，可采用迭代计算。

（3）然后，进入后续弹道ABC段修正过程。该段弹道在B点跳变是由O3的定位误差引起，位置误差分量分别为δx03、δy03、δz03，三者为常值。如果速度数量级较小可忽略不计时，借鉴OAB段弹道的步骤（2.1）的位置常值误差修正方法；否则,需要根据速度修正该段弹道的时间不对齐误差和常值误差。流程如下：

①首先，根据步骤（2）得到该段数据误差为[δXOA′-vxOA′Δt-δrx;δXA′A-vxA′AΔt-δrx-nx0-nx1;δXAB-δx02-vxABΔt-δrx;δXBB′;δXB′C]，把该段数据的速度数据vxBC代入式（4），可得

（7）

进而得到误差[δXOA′-vxOA′Δt-δrx; δXA′A-vxA′AΔt-δrx-nx0-nx1; δXAB-δx02-vxABΔt-δrx;δXBB′-vxBB′Δt-δrx; δXB′C-vxB′CΔt-δrx]。

②其次，分别计算δXAB-δx02-vxABΔt-δrx的均值为mx1，δXB′C-vxB′CΔt-δrx的均值为mx2，得到一组新的误差[δXOA′-vxOA′Δt-δrx;δXA′A-vxA′AΔt-δrx-nx0-nx1;δXAB-δx02-vxABΔt-δrx;δXBB′-vxBB′Δt-δrx;δXB′C-vxB′CΔt-δrx-mx2+mx1]。其中，δx03=δX'BC+mx2-mx1。

③最后，检验误差[δXOA′-vxOA′Δt-δrx;δXA′A-vxA′AΔt-δrx-nx0-nx1;δXAB-δx02-vxABΔt-δrx;δXBB′-vxBB′Δt-δrx;δXB′C-vxB′CΔt-δrx-mx2+mx1]各段的均值。如果基本相同，得到修正后的外测值为[XOA′-vxOA′Δt-δrx;XA′A-vxA′AΔt-δrx-nx0-nx1;XAB-δx02-vxABΔt-δrx;XBB′-vxBB′Δt-δrx;XB′C-vxB′CΔt-δrx-mx2+mx1]。一般情况下，经上述计算后即可得到满足要求的结果。如果精度要求较高时，可采用迭代计算。

2.2 测量噪声平滑方法

光电经纬仪数据处理时，常利用由位置参数微分中心平滑的方法及相应公式，获取导弹的飞行速度和加速度参数。对于非关机点附近的主动段弹道、自由段弹道和再入段弹道，通常使用速度二阶中心平滑和加速度三阶中心平滑公式处理光电经纬仪的数据。处理主动段弹道数据时,平滑区间常取为1s或2s;处理自由段弹道数据时,平滑区间一般不超过20s;再入段弹道的平滑区间为1～2s。对于关机点附近的主动段弹道，由于弹道变化剧烈，由位置参数平滑求速时，采用四阶中心平滑公式，平滑区间同二阶中心平滑[4,9,16]。

但是微分得到的数据存在跳变和噪声过大的现象，掩盖了惯性导航的速度偏值，因此需要对外测速度进行平滑滤波，以能够如实反映惯性导航速度误差的变化趋势。下面给出两种常用的滤波方法。

2.2.1 低通滤波方法

低通滤波器作为一种广泛应用的滤波器，具备保留低频信号、抑制高频信号的特点，并且性能稳定，易于调节，工程上常用于信号处理、数据传输和抑制干扰。利用这一特点，可使用在外测弹道速度和加速度参数处理中，由于弹道速度是由位置微分后得到的，周期为2s。采用如下的二阶低通滤波器

（8）

（a） f=1Hz

（b） f=0.1Hz图7 低通滤波效果对比Fig.7 Comparison of low-pass filtering effect

对速度进行再滤波时，如果转折频率大于1Hz，则滤波无效果；而如果转折频率过小，则响应能力变弱，曲线失真。图7所示为分别采用f=1Hz和f=0.1Hz对vz进行滤波的结果，图中蓝色曲线为vz滤波前的值，红色曲线为vz滤波后的值。可以看出，f=1Hz时，噪声幅值无变化；而f=0.1Hz时，噪声虽然衰减，但在信号快速变化时响应能力不够。因此，在后续分析中不选用滤波法，而采用曲线拟合方法。

2.2.2 多项式拟合算法

多项式拟合算法也叫Savitzky-Golag（SG）平滑算法，是由Savitzky和Golag提出的基于最小二乘原理的多项式平滑算法[8,10,17]。该算法的关键在于矩阵算子的求解。假定平滑滤波滑动窗口长度（数据点的个数）为k，采用n次多项式对窗口内的数据进行描述[14]，如式（9）所示。通常情况下，滑动窗口的长度和多项式拟合阶次的选择来源于工程经验。

（9）

式中，i=1,2,…,k。

将k个测量点依次代入多项式方程中，得到了k个方程组，将其转化为矩阵形式为

（10）

对以上矩阵方程采用最小二乘估计，可得到拟合参数ai（i=1,2,…,k）的估值。

3 试验结果及分析

3.1 多站交接点位置偏差修正结果

针对图4所示的由站点位置误差引起的光电外测跳变误差，采用本文方法进行修正：

（1）OAB段弹道修正

该段弹道在A点跳变是由O2的定位误差引起，位置误差分量分别为δx02、δy02、δz02，三者为常值。由于Y方向的速度分量vy相对vx和vz的值大1～2个数量级，需单独修正弹道误差。对Y方向弹道采用最小二乘法估计出站址位置误差δry=-1.266m和时间不对齐误差Δt=7.933×10-3s。修正后OAB段外测位置误差如图8所示，对比图4可以看出，这种修正方法既可辨识出站址常值误差，也可辨识出时间不对齐误差，经过补偿后实现了对OAB段弹道的精确复现。

图8 修正后的外测位置误差Fig.8 Corrected external measurement position error

（2）OABC段弹道修正

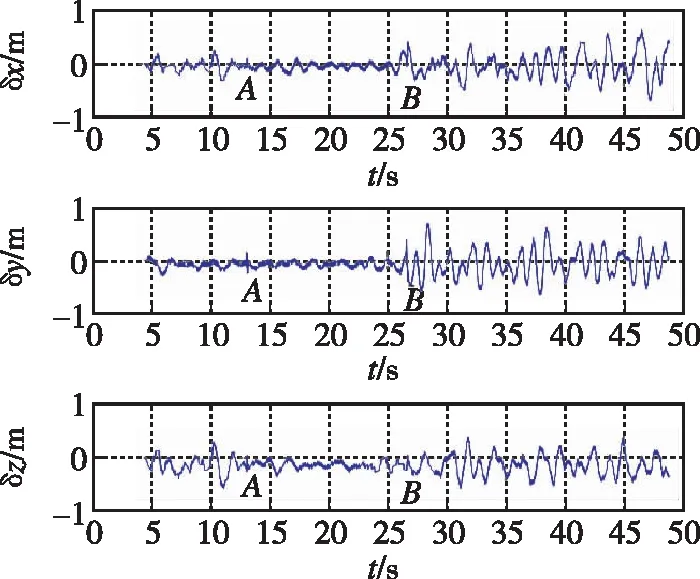
图9 修正后的外测位置误差Fig.9 External measurement position error after correction

该段弹道在B点跳变是由O3的定位误差引起，位置误差分量分别为δx03、δy03、δz03，三者为常值。针对图8所示的由站点位置误差引起的光电外测跳变误差，修正方法借鉴OAB段弹道的修正方法，但比较特殊的是δy03值的精确估计及弹道修正，仍需要修正时间不对齐引起的误差。修正后OABC段外测位置误差如图9所示，对比图4和图8可以看出，修正后的测试数据不再发生跳变，经过站址误差标定和补偿后实现了对OABC段弹道的精确复现。

经过多站交接点位置偏差修正方法，实现了站点交接引起的弹道位置偏差和时间不对齐偏差。修正后的弹道如图10中红色曲线所示，相对于修正前的蓝色曲线，弹道更加连续。

图10 修正前后的初始段弹道Fig.10 Initial trajectory before and after correction

3.2 多项式拟合平滑噪声结果

本文滑动窗口长度取光电测试数据的长度，取k=1120，n=4，对速度测量值vx、vy、vz进行平滑拟合，计算得到3个方向速度的拟合参数分别为

结果如图11所示，其中，红色曲线为速度测量值;蓝色曲线为拟合结果；黑色曲线为拟合残差。

利用上述新的外测速度值，可得到一组新的遥外测速度误差，如图12中红色曲线所示，相比修正前的蓝色曲线可以看出，数据更加平滑。

最终，对速度进行积分后可得位置信息，如图13中绿色曲线所示。可以看出，通过修正位置偏差和多项式拟合的方法,消除噪声后得到的弹道更加平滑准确，既保证了弹道曲线的连续性，又可满足弹道的平滑性。

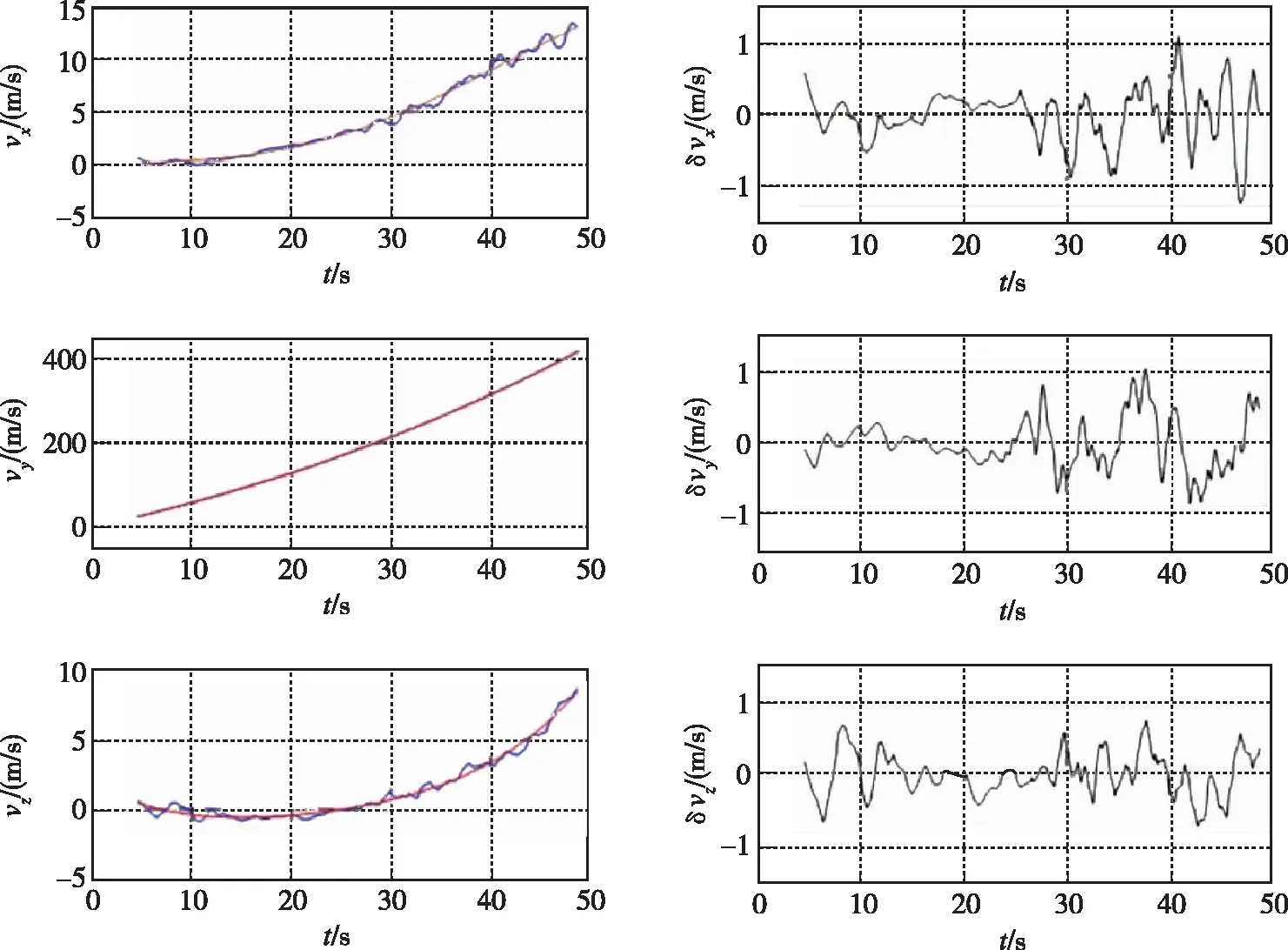
图11 速度拟合值及拟合残差Fig.11 Velocity fitting value and fitting residual

图12 惯性制导遥外测速度差Fig.12 Velocity difference of inertial guidance remote measurement

图13 修正偏差和平滑噪声前后的初始段弹道Fig.13 Initial trajectory before and after correcting bias and smoothing noise

4 结 论

在导弹试验靶场采用多套光电外测设备测量外弹道参数时，不同设备在交接工作的过程中会引起位置偏差，后续利用外测位置数据获得速度和加速度时，由于微分会存在噪声过大的现象，从而导致测量弹道不准确，不利于后续的试验分析。因此，本文提出了一种多站交接点位置偏差的修正方法，旨在通过迭代消除均值差的方式，消除测量设备交接过程中产生的常值误差和时间不对齐误差，从而达到修正位置偏差的目的，使得弹道曲线更加连续。同时，利用多项式拟合的方法缓解由微分计算速度值而带来的噪声过大的问题，使得弹道曲线更加平滑，从而较好地复现弹道飞行轨迹。但是，滤波过程中如何从理论上科学地设定算法的重要参数，使其获得最优的平滑效果，以及如何应用平滑后的运动参数，实现导弹的精度评定、制导系统工具误差分离等工作，需要进一步的研究和验证。