立方体式考夫曼离子推力器极靴结构设计*
2022-11-02周思引聂万胜朱康武朱浩然吴其骏
闫 康,周思引,聂万胜,朱康武,朱浩然,吴其骏
(1. 航天工程大学·北京·101416;2.上海航天控制技术研究所·上海·201109)
0 引 言
航天器在轨运行需要高精度的推力控制,对推力器的寿命也有很高要求,尤其在深空探测任务中,航天器有效载荷小、液体推进剂长期储存难、无补给等问题限制了航天器的寿命和载荷能力[1-2],电推进技术可以解决上述问题[3-6]。电推进是一种利用太阳能产生的电能电离推进剂工质,并加速电离工质从而产生推力的空间推进方式。各种电推进类型中,考夫曼离子推力器工质利用率高达90%,效率可达60%[7-9],寿命近万小时,在空间电推进领域应用中占比非常大,是未来航天器推进技术发展的重要方向之一。
对于离子推力器,磁场位形在很大程度上决定了电离率,进而影响了推力器核心性能。围绕考夫曼离子推力器放电室磁场设计,国内外开展了众多研究:M.J.Patterson等[10-11]针对30cm考夫曼离子推力器进行研究,发现放电室内磁场等值线在0.005T时,放电室壁面电流损失降低了10%;在RC3考夫曼离子推力器[12]、BBM-1推力器[13]和美国的NEXT推力器[14]的研究过程中,也都对阴极极靴位形进行了试验,发现存在一个最优值,使得推力器的核心性能参数达到最优。
极靴会引导磁力线在放电室内的走势,进而对放电室内电子密度和电子温度等参数产生影响,是决定推力器性能的重要因素之一。为此,通常需要开展大量的地面试验以优化极靴结构设计,但是大量电推进地面试验需要消耗大量的推进剂,导致试验成本很高,试验周期较长。随着计算机软硬件的飞速发展,通过数值仿真对多物理场模拟已成为可能,采用数值仿真手段研究离子推力器工作性能参数,已成为当前电推进研究领域的趋势。
当前对考夫曼离子推力器的设计研究,大都是圆柱形和锥形-直段形结构[15-16],然而绝大多数卫星采用立方体构型。从制造和装配的角度看,推力器采用立方体构型较传统构型更有优势,有利于快速批量化生产。鉴于此,本文针对自主设计的立方体式考夫曼离子推力器,开展了阴极极靴结构设计研究,通过数值仿真手段获得了不同阴极极靴结构下的放电室特征参数,给出了阴极极靴设计建议。
1 推力器工作原理与研究工况
1.1 立方体式考夫曼离子推力器介绍
自主设计的立方体式考夫曼离子推力器结构如图1所示,采用柱状永磁体(铷铁硼Nd-Fe-B),极靴可以引导放电室内部的磁场分布,达到磁场强度要求,也满足磁钢对工作温度的条件,降低了设计和试验难度。推力器整体为长方体结构,相较于圆柱形推力器,航天器在运行过程中长方体不易滚动,质心不容易发生偏移,且易于模块化组装。考夫曼型离子推力器根据磁场结构可分为强发散场、环形会切场、柱形会切场三种类型,本文研究关注的是小功率离子推力器,通常选择强发散场直流放电室结构,其磁场位形布局相对简单,体积小,质量小。离子推力器工作时,主阴极发射电子在电场作用下进入放电室内,磁场约束电子在放电室内且增加运动路程,在与电场的共同作用下,电子与工质发生碰撞产生离子,离子通过栅极加速引出。为防止离子在航天器表面附着等情况影响航天器本体电位,中和器产生电子在电场作用下与出口离子束流进行中和。

图1 立方体式考夫曼离子推力器结构图Fig.1 Cube Kaufman ion thruster structure diagram
1.2 研究工况
参考LIPS-100圆柱形离子推力器[17]阴极极靴内径,以及SERT-II圆柱形推力器[18]阴极极靴长度和内径值,根据考夫曼离子推力器阴极极靴初步设计经验式(1)和式(2),选取立方体阴极极靴径向截面为长方形结构,长度范围为15~25mm,长宽等比例变化,阴极极靴深入放电室内部10mm。
DK≈0.4Dd
(1)
LK≈0.5DK
(2)
式中,DK为阴极极靴内径;Dd为放电室口径;LK为阴极极靴长度。
推力器阴极极靴设计依据经验式(1)和式(2),选取三种不同极靴结构进行研究,具体构型尺寸如表1所示。

表1 阴极极靴五种结构
2 数值仿真模型与方法
2.1 数值计算模型
电子密度ne和电子能量密度nε分别由漂移扩散方程式(3)~式(10)计算
(3)
(4)
De=μeTe
(5)
Dε=μεTe
(6)

(7)
(8)
(9)
(10)
电子源与电子能量损失的计算式为
(11)
式中,M为参与电子变化反应的数量;P为非弹性电子与中性碰撞反应的数量;xj为关于反应j中目标物的摩尔分数;kj为反应j速率系数(m3/s);Nn为中性粒子数密度(/m3);Δεj为反应j中损失的能量(eV)。
由于永磁体产生强磁场,故电子迁移率计算式为
(12)
式中,μdc为无磁场情况下的电子迁移率(m2/(V·s));Bx、By和Bz分别为磁场在x、y和z方向上的磁场分量(T)。
2.2 初始条件
根据离子推力器试验结果[19],数值模拟中电子与氙离子初始密度为1×1017/m3,空心阴极产生电子速率为4.2×1024/(m3·s)[20],电子初始温度为4eV,放电室内压强为0.1Pa,阳极电压为40V,阴极极靴与屏栅极电压为0V。
2.3 边界条件

图2 推力器三维模型Fig.2 3D model of thruster
由于设计推力器为立方体式,所以不能采取二维轴对称简化计算模型,实际计算区域为整个三维立方体离子推力器,如图2所示。设置空心阴极发射的电子在底部阴极极靴中心释放,经过阳极的电场和极靴引导的磁场共同作用下,进行霍尔漂移运动,并和中性粒子发生碰撞电离等,其中部分电子和离子与极靴、阳极和放电室内壁发生碰撞,电子到达放电室出口都视为消失,不考虑电子二次发射。
2.4 稳定性条件
数值计算中的空间步长和时间步长对计算稳定性有着决定性影响,根据导心理论[21],带电粒子在一定距离内自身电场会对外部电场产生影响,所以网格划分中需要考虑德拜长度[22],时间步长设置应小于回旋频率的倒数[23]。
(13)
式中,λD为德拜长度(m);ε0为真空介电常数(8.85×10-12F/m);k为玻耳兹曼常数(1.38×10-23J/K);ni为氙离子密度(/m3);e为带电粒子电荷量;电子温度Te取4eV。
(14)
式中,m为氙离子质量(2.18×10-25kg);ωp为回旋频率;求出时间步长dt<1.7677×10-8。
考虑数值计算收敛问题[24],由能量守恒定律求出最大速度和时间步长
(15)
(16)
式中,Δφ为阳极与入口处电势差(V);dl为网格边长(m);vmax为最大速度(m/s)。综合考虑,本模型网格边长需小于德拜长度λD:max(Δx,Δy,Δz)<1×10-5m,Δx、Δy、Δz分别为每个网格在x、y、z方向上的变化量(m);时间步长取dt=1×10-10s。
3 结果与讨论
图3所示为不同极靴结构瞬态放电室内磁场分布和电子密度分布云图。磁力线由磁铁发出,经极靴引导至放电室内部。纵向对比不同结构工况可见,随着阴极极靴内径增大,磁场的均匀性和强度逐渐下降。结构一和结构二的磁场分布明显不对称,随着内径增大,放电室中心磁场强度下降,电子的运动路程发生变化,电子密度最大值从3.5×1018/m3降至4.12×1017/m3;但是电子密度分布有所改善,电子密度最小值从1.27×1014/m3提高至3.97×1014/m3。
图4给出了放电室出口沿径向的离子密度分布。可以看出,阴极极靴的直径在一定范围内变化时,其引导的放电室内磁场分布不同,随着放电室内电子密度逐渐上升,放电室出口处离子密度峰值先增大后减小。总体上,离子推力器出口处离子密度都符合对称式波峰分布[25-27],阴极极靴在五种不同内径情况下,结构二和结构五的推力器出口离子密度分布对称性较差,对栅极侵蚀和寿命有较大影响,导致推力密度分布不均匀;结构三比结构一的平均出口离子密度高出9.36%,虽然结构三比结构四的平均出口离子密度高出1%,但是结构三出口的离子密度分布相比结构四较差,所以结构四综合性能较好。对称轴上离子密度较高,其栅极系统通过率会相对降低,抑制了出口中心处束流的离子数量;出口边缘离子密度相对较低,其栅极系统通过率高于出口中心处,故束流的离子密度分布较屏栅前会更均匀[28]。

(a) 结构一

(b) 结构二

(d) 结构四

(e) 结构五图3 五种结构的磁场和电子密度分布Fig.3 Magnetic field and electron density distributions for five structures
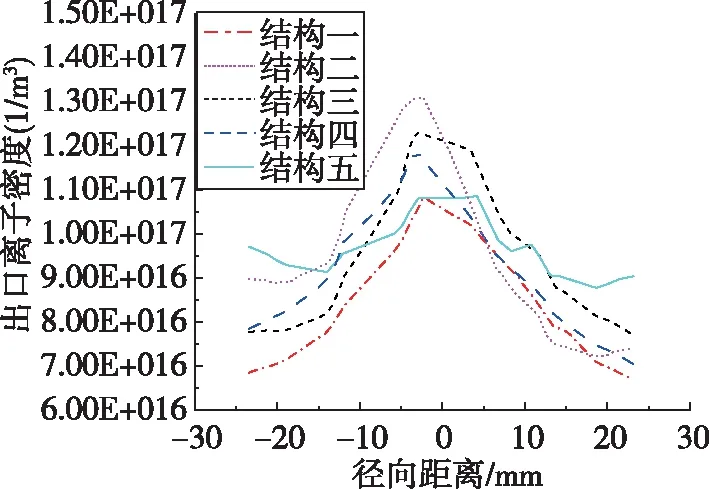
图4 放电室出口离子密度Fig.4 The ion density at the outlet of the discharge chamber
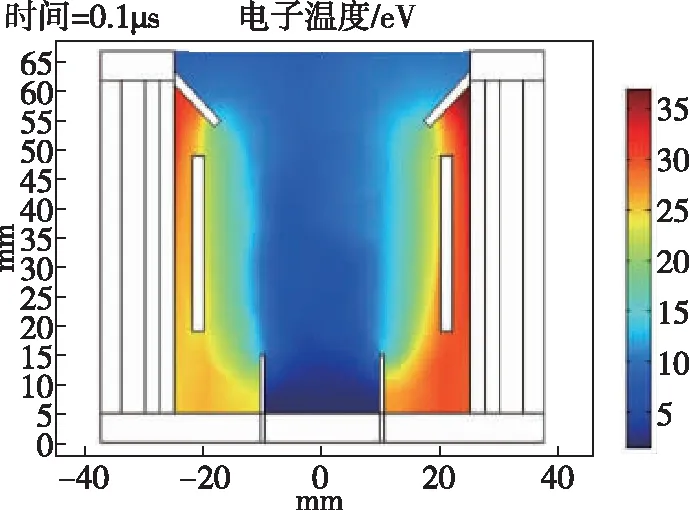
从五种结构放电室的电子温度分布(图5)发现,电子在磁力线的约束下与中性粒子发生碰撞电离产生离子,当极靴内径增大,极靴引导的磁力线外移,电子沿磁力线径向范围增大,电离区域增大,所以该区域电子温度相对较低[29]。随着阴极极靴内径的减小,较低的电子温度区域(蓝色部分)分布在屏栅极靴和阴极极靴之间磁场线轮廓内部。对比电子温度云图(图5)与磁场分布结果(图3)发现,电子温度的梯度轮廓与磁力线比较重合。由于电子具有一定的初始能量,除了电场作用外,粒子间碰撞会使得电子温度发生变化,结构一和结构二相比其他三种结构,放电室中心电子温度较低区域大,反映电离程度较高[30]。但如图6所示,随着阴极极靴内径的减小,放电室内电子温度逐渐增加,发散场的电子在放电室内壁附近温度会骤然升高,主要是因为放电室内壁附近的磁场强度比放电室中心要小,磁场对电子的约束较弱,使内壁附近的电子容易与壁面发生碰撞而损失能量,在内壁附近形成鞘层[31];其次,放电室内壁附近的电子获得能量后,在放电室轴向运动中会与气体工质发生非弹性碰撞,能量也会损失[32],所以放电室内壁附近的电子温度较高[33]。在实际工作中,放电室开始点火后内部温度逐渐升高至平稳,会影响电子的初始速度,电子的拉莫尔半径会增大,在保证电子能被磁场约束在阳极内部的前提下,遵循放电室出口离子密度和分布等条件,考虑阴极极靴结构时优选结构四。

(a) 结构一
(b) 结构二

(c) 结构三

(d) 结构四

(e) 结构五图5 中心截面处电子温度分布Fig.5 Electronic temperature distribution at the central section

(a) 径向电子温度

(b) 轴向电子温度图6 径向与轴向电子温度分布Fig.6 The distribution of electron temperature in the radial and axial directions
4 结 论
本文针对自主设计的立方体式考夫曼离子推力器,建立等离子运动过程的三维粒子数值模型,开展了三维数值仿真研究,对比分析了不同极靴内径引导的放电室磁场分布,主要结论如下:
1)对于五种阴极极靴结构,随着极靴内径的增加,电子径向运动范围增大,电子密度分布更均匀;但是极靴内径增加可能会降低推力器总性能,体现在放电室内壁电子温度逐渐增大,电子损耗增大。
2)随着极靴内径的增加,磁力线约束的范围增大,电子与中性粒子碰撞电离范围增大,出口离子密度分布均匀;但是放电室中心磁场强度降低,放电室出口处离子密度呈现下降趋势,导致推力器性能下降。
对于本文涉及的立方体考夫曼离子推力器,长宽高为15mm×12.5mm×15mm的阴极极靴构型最佳,既可保持较低的壁面电子温度,又有利于推力器出口的离子均匀性。
