行星滚柱丝杠螺纹副-齿轮副同步啮合动态接触载荷特性

2022-11-02马腾龙马尚君吴林萍付晓军许千斤刘更

西安交通大学学报 2022年10期

马腾龙,马尚君,2,吴林萍,付晓军,许千斤,刘更,2

(1.西北工业大学陕西省机电传动与控制工程实验室,710072,西安;2.西安鼎佰精密机电有限公司,710199,西安)

contact load

行星滚柱丝杠(planetary roller screw mechanism, PRSM)是一种可将旋转运动和直线运动相互转化的精密机械传动机构[1],具有螺纹副和齿轮副同步啮合特征。PRSM以其承载能力强、精度高、抗冲击等特点,逐步成为航空、航天、航海等军事领域装备和石油化工、食品包装、过程控制等民用领域机械装备直线伺服系统的主要执行机构之一。

行星滚柱丝杠具有螺纹副-齿轮副同步啮合的复杂结构,国内外对于PRSM螺纹副的动态接触特性已经有一定研究基础:Velinsky等[2]研究了PRSM中滚柱和螺母之间的轴向滑移,建立了滚柱在丝杠和螺母接触点处的轴向滑移速度的运动学模型;Abevi等[3]以反向式PRSM为对象,采用3D有限元方法研究了螺纹在重载条件下的静态接触行为及接触压力分布,获得了拉压条件下系统的轴向刚度和载荷分布;马尚君等[4-5]分析了反向式PRSM中滚柱位移对机构导程和滑动速度的影响,并得到了与Jones等[6-7]相同的结论,即滚柱节圆的偏移不会影响机构导程,并且建立了考虑不同螺纹旋向的分析模型,基于行星传动的原理揭示了各构件参数间的关系;付晓军等[8]建立了非线性六自由度刚体动力学模型,研究了重载和轻载等工况下PRSM的瞬态和稳态动力学行为;张文杰等[9]总结了PRSM安装方式并进行了受力分析,综合PRSM接触刚度、螺纹牙刚度和轴段刚度,建立了计算PRSM螺纹牙载荷分布的数学模型;佟瑞庭等[10]建立了单对滚柱与丝杠啮合副的接触模型,分析了螺纹牙型角对行星滚柱丝杠接触特性的影响;郭辉等[11]基于螺纹牙载荷分布和螺纹牙受载变形关系,提出了滚柱螺纹牙的修形方法,得到了修形量最优值;姚琴等[12]以赫兹接触理论及弹塑性力学为基础,建立了丝杠与滚柱单对接触模型,分析了载荷与行星滚柱丝杠副弹塑性接触变形的关系;杨家军等[13]基于赫兹弹性接触理论,分析了行星滚柱丝杠的载荷分布规律,并建立了新的静刚度数学模型;郭嘉楠等[14]依据赫兹接触理论建立了考虑螺纹啮合刚度的行星滚柱丝杠动力学模型,分析了螺纹接触角和滚柱半径对啮合刚度和固有频率的影响规律;付永领等[15]基于载荷分布规律,研究了负载对摩擦力矩的影响规律;郑正鼎等[16]基于空间啮合理论与赫兹接触理论,分析了差动式行星滚柱丝杠承载特性;刘柱等[17]提出了考虑滚柱弯曲变形时的标准型行星滚柱丝杠副的载荷分布计算方法,分析与研究了螺纹误差和装配误差对行星滚柱丝杠副载荷分布规律的影响。PRSM齿轮副具有内啮合和行星传动特征,其啮合接触特性对承载及螺纹副-齿轮副同步啮合特性有重要影响。周建星等[18]采用集中质量方法建立了行星齿轮传动系统碰撞振动分析模型,分析了负载和转速对啮合接触力的影响;陶庆等[19]采用有限元方法建立了行星齿圈结构模型,依据啮合力与内齿圈的变形协调关系建立了传动系统刚-柔耦合动力学模型;王成龙等[20]采用有限元方法建立齿圈结构动力学分析模型,将内齿圈各轮齿啮合区进行划分,用轮齿承载接触分析(LTCA)方法确定齿间载荷分配关系,计算了不同载荷下内齿圈齿根动应力；冯诗愚等[21]采用线弹性理论,建立了内啮合齿面接触力计算的数学模型,分析了间隙对内啮合接触力的影响规律。

现有研究为PRSM的静动态运动特性分析奠定了重要基础,但分析模型多局限于螺纹部分静态和动态接触分析,未充分反映螺纹副-齿轮副同步啮合动态接触、参数间耦合作用及其对系统动力学响应研究的规律;而且动力学研究主要以刚体为主,引起接触状态变化的潜在因素尚不清楚。因此,需要建立考虑螺纹副和齿轮副同步啮合的新模型,来进一步研究动态接触载荷特性。

本文基于PRSM运动学原理,采用有限元方法建立了数值模型,进行运动学及动力学仿真分析。在验证数值模型正确性的基础上,研究了滚柱-丝杠侧与滚柱-螺母侧动态接触载荷、齿轮副动态接触载荷、滚柱轴端与保持架接触载荷的变化规律以及不同螺母负载、丝杠转速、摩擦系数对PRSM动态接触特性的影响规律,为揭示螺纹副-齿轮副同步啮合耦合动态接触载荷特性奠定理论基础。

1 PRSM运动原理

1.1 PRSM结构及工作原理

本文以标准式PRSM为研究对象,即丝杠为主动件,丝杠的旋转运动通过滚柱的行星运动转换为螺母的直线运动,其结构如图1所示。图1中丝杠1是牙型角为90°的多头螺纹,滚柱3是具有相同牙型角的单头螺纹,其牙型轮廓通常加工成球面,目的是提高承载能力。螺母2是具有与丝杠相同头数和牙型的内螺纹。若干个滚柱沿丝杠圆周方向均匀分布,当丝杠旋转时,滚柱既绕着丝杠轴线公转,又绕自身轴线自转。滚柱与螺母具有相同的螺旋升角,与螺母啮合时能够确保纯滚动并且没有相对轴向位移。为消除丝杠螺旋升角对滚柱产生的倾斜力矩,在滚柱两端加工有直齿,与内齿圈4啮合,以确保滚柱轴线平行于丝杠轴线而正常滚动;5为滚柱保持架,使滚柱沿圆周均匀分布。

1.2 PRSM运动分析

标准式PRSM运动简图如图2所示[22],A为滚柱的起始位置,E点为丝杠转动一周后滚柱的终点位置。dN、dR、dS分别是螺母、滚柱、丝杠的螺纹中径,dP为滚柱公转直径,ωS为丝杠转动角速度,ωR为滚柱绕自身轴线的自转角速度,ωP为滚柱公转角速度,φslide为纯滑动部分的相对转角。

由于滚柱和螺母螺旋升角相同,通常螺母与负载相连,采用止转结构约束其周向自由度,因此滚柱和螺母无相对轴向位移。接触点A为速度瞬心,则可求得滚柱中心O点的速度表达式

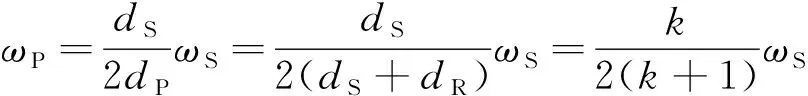
(1)

式中k为丝杠与滚柱的螺纹中径之比。

规定丝杠旋转一周后,滚柱公转角度为φP,绕自身轴线自转角度为φr,在纯滚动状态下,滚柱自转转过的弧长与在螺母上滚动的弧长相等,即

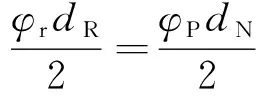
(2)

由此可得

(3)

由于φr/φP=ωR/ωP,与式(1)、式(2)联立得

(4)

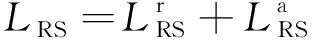
(5)

(6)

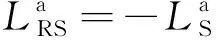
(7)

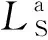
(8)

式中nS为丝杠螺纹头数。

根据图2中零件相对转角位置关系,可得

φNP+φslide+φP=2π

(9)

由式(5)～(9)得

(10)

当丝杠与滚柱之间发生相对滑动时,根据转角之间的相互关系,丝杠应与滚柱的旋向相反,即

(11)

LRS=nSP

(12)

LRS即为丝杠旋转一周后螺母的直线位移。当丝杠转动任意角度时,螺母的直线位移可表示为

(13)

对式(13)中时间t求导,可得螺母的直线速度

(14)

1.3 PRSM受力分析

PRSM承载后螺纹牙间产生的接触载荷沿其空间螺旋曲面法线方向,可将螺纹牙法向接触载荷分解为3个方向的分力,如图3、图4所示。

图3 行星滚柱丝杠滚柱和丝杠侧受力分析 Fig.3 Force analysis at the planetary roller screw screw-roller interface

图4 行星滚柱丝杠滚柱和螺母侧受力分析Fig.4 Force analysis at the planetary roller screw roller-nut interface

根据受力分析,Fn、Fa、Ft、Fr有如下的关系

Ft=Fatanλ

(15)

Fr=Fatanβ

(16)

(17)

式中:Fa为螺纹牙法向接触载荷轴向分力;Fn为螺纹牙法向接触载荷;Ft为螺纹牙法向接触载荷切向分力;Fr为螺纹牙法向接触载荷径向分力;λ为螺旋升角;β为牙侧半角。

现有文献关于PRSM的受力分析多集中于螺纹部分受力,同时考虑多个啮合副的受力较为复杂,但还没有有效手段,故本文采用有限元方法建立螺纹副-齿轮副同步啮合数值模型进行动态接触载荷特性分析。

2 数值模型

2.1 PRSM模型简化

本文研究对象的螺纹副和齿轮副参数如表1、表2所示。

表1 行星滚柱丝杠螺纹副参数

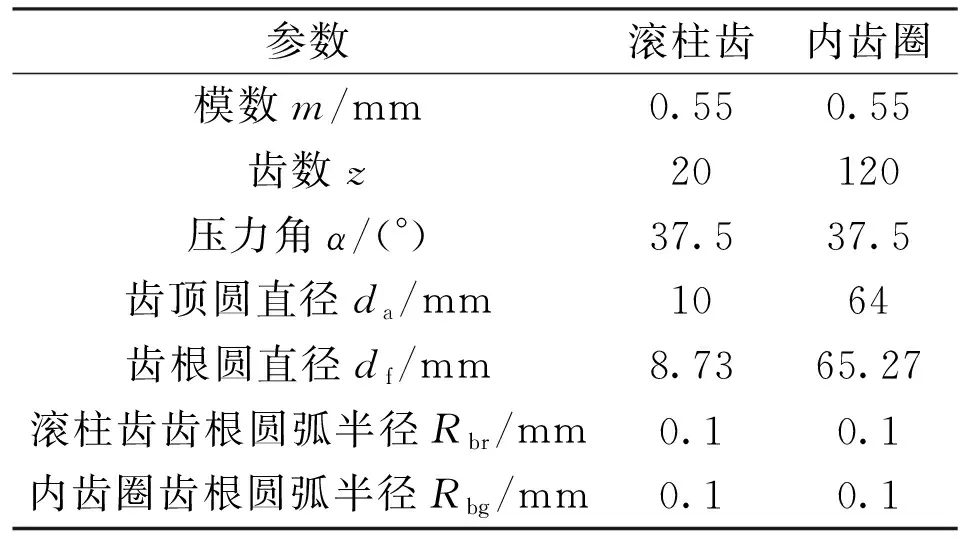
表2 行星滚柱丝杠齿轮副参数

由图1可知PRSM为循环对称结构,多个滚柱均布在丝杠周围,负载均匀施加于螺母上。对有限元模型进行合理简化[3]:①保留丝杠、滚柱、螺母、内齿圈及保持架等主要零件,省略挡圈、销轴等零件,其作用可通过有限元模型中约束条件代替;②为节省计算时间,保留3个滚柱,呈均匀分布,保证受力均布,且每个滚柱保留5个螺纹牙;③PRSM中各零件倒角和圆角在模型中忽略。

简化后的PRSM有限元模型如图5所示,螺纹副和齿轮副接触区域密化如图6所示,单元类型为Tetrahedrons四面体网格,共有955 519个单元,1 555 868个节点,选用的材料均为GCr15,密度ρ为7 810 kg/m3,弹性模量E为212 GPa,泊松比μ为0.29。

图5 行星滚柱丝杠有限元模型Fig.5 Finite element model of the PRSM

图6 行星滚柱丝杠螺纹副和齿轮副接触区域网格密化图 Fig.6 Mesh density diagram of contact area between planetaryroller screw thread pair and gear pair

2.2 边界条件

位移边界条件是:丝杠只作旋转运动,给丝杠施加旋转副;螺母只作直线运动,在螺母上添加移动副;内齿圈与螺母固定,对内齿圈添加移动副;滚柱既做自转运动,又做公转运动,在滚柱与保持架之间施加旋转副(相当于滚柱的自转),给保持架添加圆柱副(相当于滚柱公转并可伴随螺母一起移动)。接触分别为滚柱和丝杠、螺母螺纹副接触、滚柱齿和内齿圈之间的齿轮副接触、滚柱和保持架之间的接触。

力边界条件是丝杠施加转速,螺母施加与运动方向相反的轴向负载。丝杠转速方向和螺母负载施加位置及方向如图5所示。

2.3 模型验证

2.3.1 运动学验证

施加5 kN螺母轴向负载,计算丝杠旋转角速度分别为10、20、30 rad/s时螺母的轴向位移和轴向速度,由文献[23]可知,上述运动特性曲线在初始极短时间内发生振动后趋于稳定,通过前期试算,设置数值模拟时间为0.02 s,即可获得较为稳定的位移和速度曲线,计算结果如图7、图8所示。

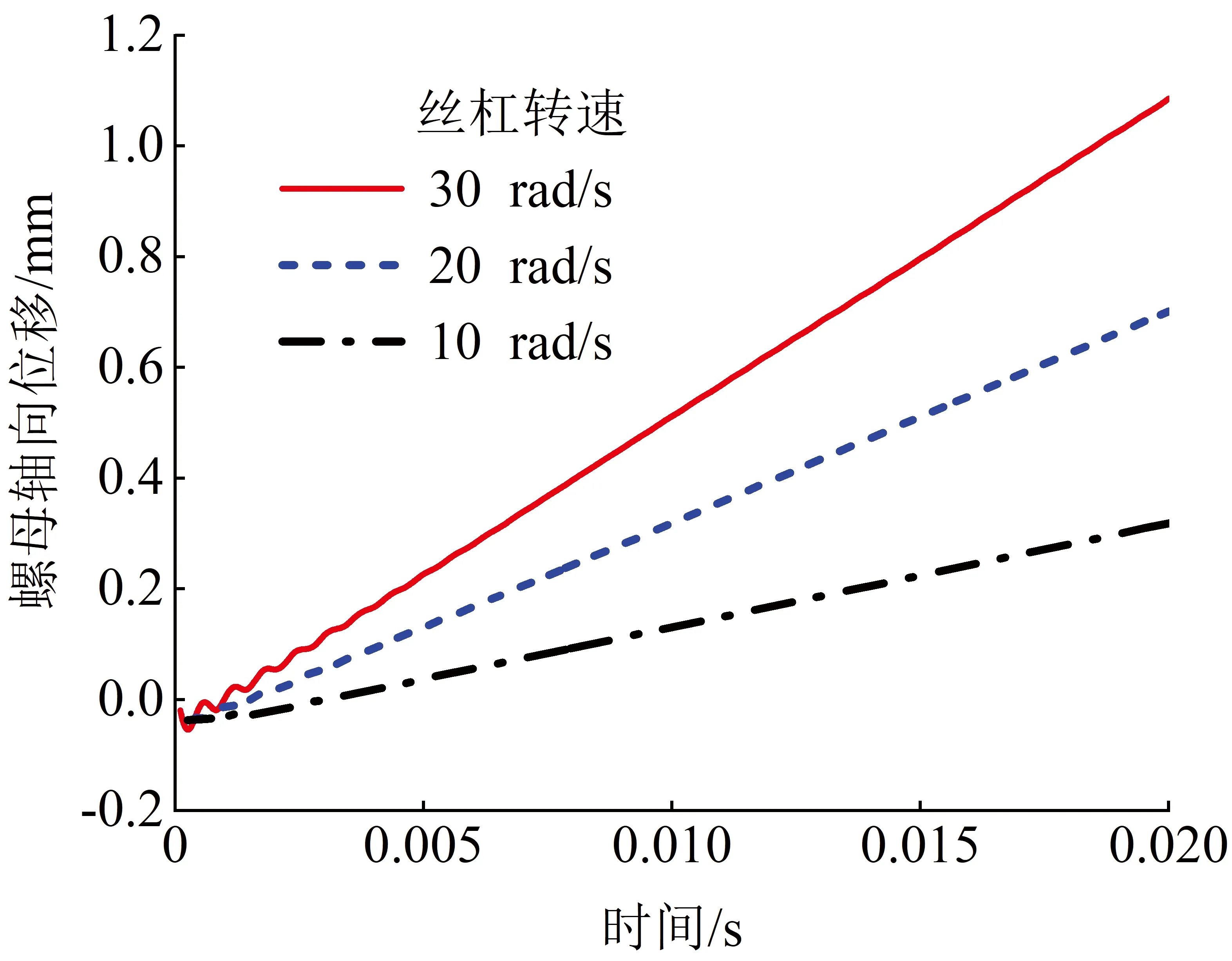
图7 行星滚柱丝杠螺母轴向位移Fig.7 Axial displacement of planetary roller screw nut

图8 行星滚柱丝杠螺母轴向速度Fig.8 Axial speed of planetary roller screw nut

由图7、图8可知,数值模型求得螺母的轴向位移分别为0.319、0.701、1.086 mm,轴向速度稳态均值分别为18.556、38.148、56.828 mm/s。图8中螺母轴向速度出现波动,是由于启动时存在装配间隙易发生打滑现象,导致初始波动幅度较大;开始运转后,在轴向载荷作用下,随着接触点增多,速度波动减小,运转趋于平稳。随着转速增加,螺母轴向速度初始阶段曲线的波动幅度也对应增加。

将表1、表2参数代入式(13)、式(14),可得不同丝杠转速下螺母的轴向位移和速度的解析解,对比结果如表3、表4所示。

表3 行星滚柱丝杠螺母轴向位移解析解与数值解对比

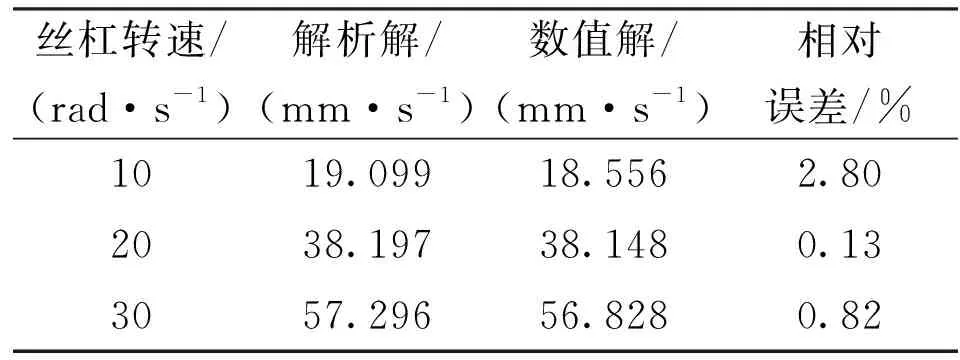
表4 行星滚柱丝杠螺母轴向速度解析解与数值解对比

由表3、表4对比结果可以看出,螺母轴向位移和速度的解析解和数值解吻合较好,相对误差均在5%以内,从运动学角度验证了该数值模型的正确性。

2.3.2 载荷验证

现有关于PRSM的接触载荷研究主要集中于螺纹副,鲜有考虑螺纹副-齿轮副同步啮合时各啮合副的接触载荷变化规律。为了便于载荷对比,本文数值模型仅提取螺纹副载荷与已有文献进行对比。文献[24]研究表明,PRSM在轴向载荷作用下,丝杠、滚柱及螺母都将发生弹性变形,并建立了螺纹牙静态载荷分布的弹簧组模型,根据变形协调与受力平衡关系构建线性方程组,载荷分布计算式

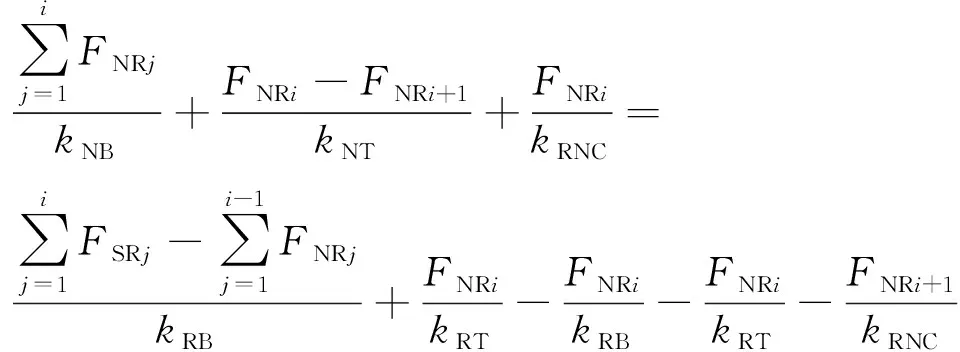
(18)

式中:i、j为PRSM螺纹牙序号;kNB为PRSM螺母螺纹轴段刚度;kRB为PRSM滚柱螺纹轴段刚度;kNT为PRSM螺母螺纹牙刚度;kRT为PRSM滚柱螺纹牙刚度;kRNC为PRSM滚柱螺纹牙轴向接触刚度;FNRj为滚柱螺母侧第j个螺纹牙所受轴向载荷;FSRj为滚柱丝杠侧第j个螺纹牙所受轴向载荷。

基于文献[24]螺纹牙载荷分布模型,结合本文模型参数,对螺母施加负载5 kN,计算得到螺纹牙轴向静载荷分布如图9所示。由图9可知,滚柱-丝杠侧和滚柱-螺母侧的各螺纹牙轴向载荷均值差异较小,约为0.333 kN,对各螺纹牙载荷求和可进一步得到整个滚柱与丝杠、螺母之间的轴向载荷为1.667 kN,根据式(17)及表1中的参数数据,可求得滚柱静载下螺纹副法向接触载荷理论值为2.363 kN。

图9 行星滚柱丝杠螺纹牙载荷分布Fig.9 Load distribution of planetary roller screw threaded teeth

以丝杠转速为30 rad/s、螺母负载为5 kN、摩擦系数为0.02为例进行数值模拟,得到滚柱-丝杠侧和滚柱-螺母侧动态接触载荷曲线,并与通过载荷分布模型求得的滚柱静载下螺纹副接触载荷理论值曲线进行对比,如图10所示。

图10 行星滚柱丝杠螺纹副动-静载荷结果对比Fig.10 Comparison of dynamic and static load results of planetary roller screw thread pairs

由图10可知:螺纹副动态接触载荷在静态接触载荷附近波动,当螺纹副承载达到稳态后,动态接触载荷与静态接触载荷趋于一致,但动态接触载荷较静态理论值偏大,其中丝杠侧为2.381 kN,螺母侧为2.372 kN,除了受齿轮副啮合激励的影响外,螺纹副和齿轮副同步啮合产生变形后的耦合作用也是导致动态接触载荷产生波动且大于静态理论值的主因之一,相对误差较小,分别为0.76%、0.38%,因此从承载的角度验证了有限元模型的正确性;滚柱与丝杠侧的接触载荷波动程度比滚柱与螺母侧大,主要原因是滚柱与丝杠侧的接触点偏离滚柱螺纹中径,滚柱与丝杠侧为滚滑并存的传动模式[25],滑动摩擦的存在也是导致接触载荷波动的原因之一。

3 PRSM动态接触特性分析

3.1 啮合副动态接触载荷分析

按照前述有限元模型工况及参数设置,对参与啮合的零件动态接触载荷进行分析。仿真得到螺纹副滚柱-丝杠侧和滚柱-螺母侧动态接触载荷曲线、齿轮副动态接触载荷曲线、滚柱轴端与保持架动态接触载荷曲线，如图11～13所示。

图11 行星滚柱丝杠螺纹副动态接触载荷Fig.11 Dynamic contact load of planetary roller screw thread pair

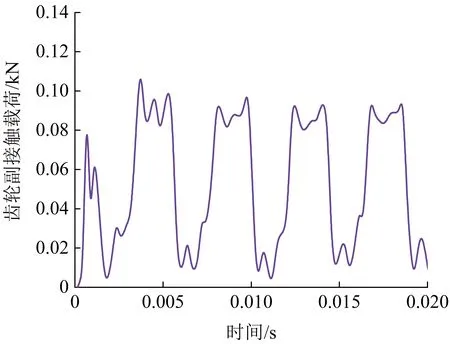
图12 行星滚柱丝杠齿轮副动态接触载荷Fig.12 Dynamic contact load at the planetary roller screw gear pair

图13 行星滚柱丝杠滚柱轴端与保持架动态接触载荷Fig.13 Dynamic contact load at the planetary roller screw roller-retainer

由图11可知,滚柱和丝杠侧稳态接触载荷均值为2.381 kN,滚柱和螺母侧稳态接触载荷均值为2.372 kN,滚柱-丝杠侧动态接触载荷大于滚柱-螺母侧动态接触载荷,主要原因是滚柱与螺母接触侧为内螺旋曲面接触,接触面积略大于滚柱与丝杠侧。0.008 s之前两接触侧接触载荷均出现波动,0.008 s对应螺母轴向位移为0.4 mm,表明0.008 s之后螺纹副已消除间隙,发生变形使接触面积增大,接触点增多,故接触载荷达到稳定状态。由于螺纹副-齿轮副同步啮合,螺纹副受齿轮副啮合激励的影响,稳态后仍然呈现微幅波动。由图12可知,齿轮副接触载荷呈现周期性波动,具有与直齿轮副啮合相似的动态运动特性,稳态后的均值约为0.059 kN。由图13可知,滚柱轴端与保持架稳态后的接触载荷均值约为0.61 kN,其承受的载荷为齿轮副的10.3倍,故该位置的承载特性应在设计PRSM时予以考虑。此外,滚柱轴端与保持架动态接触载荷受齿轮副激励的影响较为显著,同样呈现周期性波动。

3.2 转速对啮合副动态接触特性的影响

以螺母负载为5 kN,丝杠转速分别为10、20、30 rad/s为例,不同丝杠转速下滚柱-丝杠侧和滚柱-螺母侧动态接触载荷、齿轮副动态接触载荷、滚柱轴端与保持架动态接触载荷变化规律如图14～17所示。

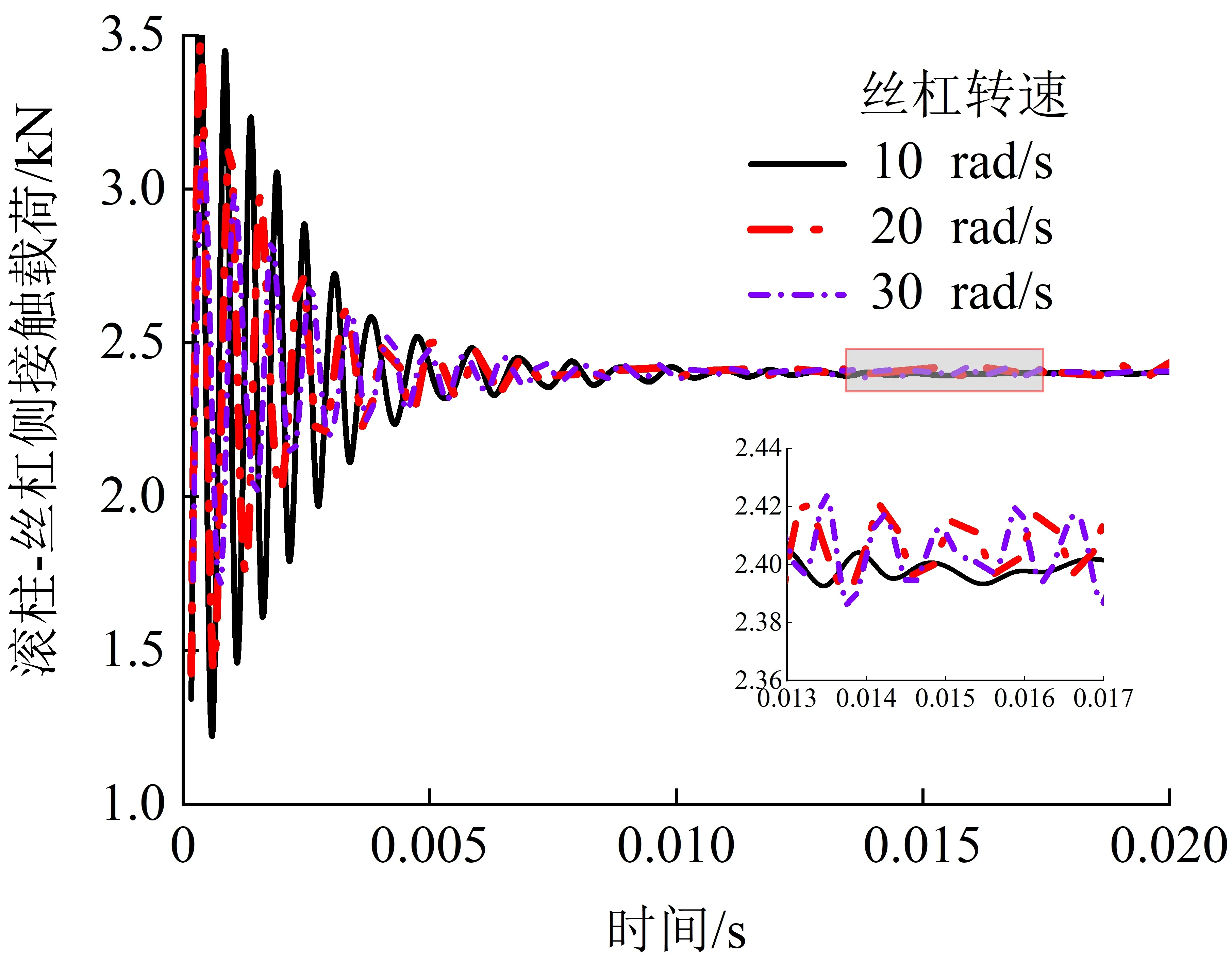
图14 不同转速下滚柱-丝杠侧动态接触载荷Fig.14 Dynamic contact load at the roller-screw interface at different speeds

图15 不同转速下滚柱-螺母侧动态接触载荷Fig.15 Dynamic contact load at the roller-nut interface at different speeds

图16 不同转速下齿轮副动态接触载荷Fig.16 Dynamic contact load at the gear pair at different speeds

图17 不同转速下滚柱轴端与保持架动态接触载荷Fig.17 Dynamic contact load at the roller-retainer at different speeds

与前述接触载荷曲线变化规律相似,各个接触副动态接触载荷曲线初始阶段均存在波动。对比图14、图15和图17可知,齿轮副接触载荷波动变化较小,因为实际工作中,PRSM承载后,螺纹副先接触,较高的转速会使螺纹副产生冲击振动,对齿轮副的影响较小。由图14、15可知,丝杠转速增加时,滚柱-丝杠侧与滚柱-螺母侧之间可以尽快消除间隙,而动态接触载荷达到平稳的时间也就越短,同时曲线波动也对应增加。

对于具有周期性的齿轮副和滚柱轴端与保持架来说,根据式(4)可知随着丝杠转速增大,滚柱转速增大,由齿轮副啮合频率计算公式:啮合频率=齿轮转频×齿轮齿数,可知啮合频率增大,进而啮合周期减小并产生一定相位差,验证了图16、17所示的动态接触特性规律。

3.3 负载对啮合副动态接触特性的影响

以丝杠转速为30 rad/s，螺母负载分别为5、6、7 kN为例,不同螺母负载下滚柱-丝杠侧和滚柱-螺母侧动态接触载荷、齿轮副动态接触载荷、滚柱轴端与保持架动态接触载荷的影响规律如图18～21所示。

图18 不同负载下滚柱-丝杠侧动态接触载荷Fig.18 Dynamic contact load at the roller-screw interface at different loads

图19 不同负载下滚柱-螺母侧动态接触载荷Fig.19 Dynamic contact load at the roller-nut interface at different loads

图20 不同负载下齿轮副动态接触载荷 Fig.20 Dynamic contact load at the gear pair at different loads

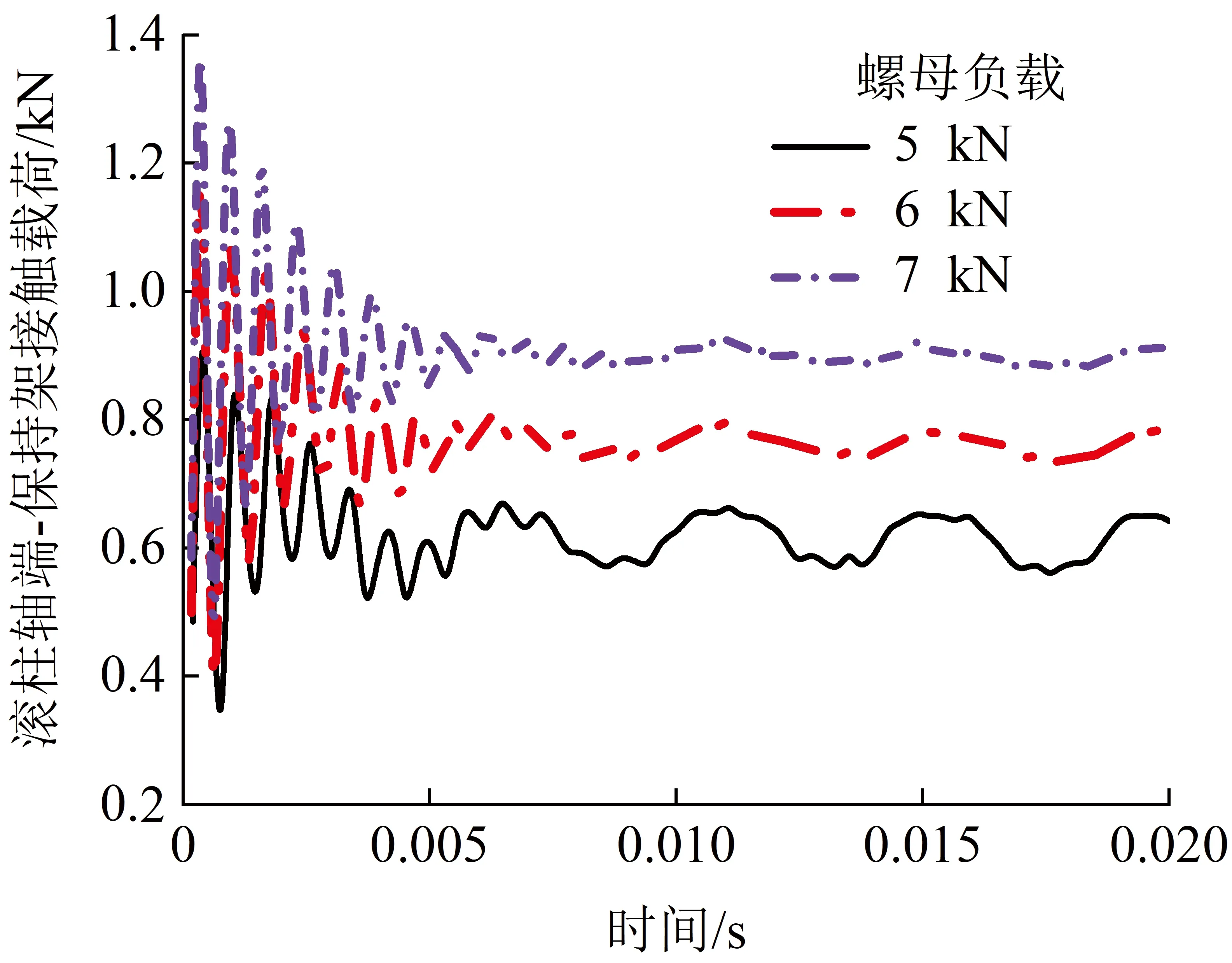
图21 不同负载下滚柱轴端-保持架侧动态接触载荷 Fig.21 Dynamic contact load at the roller-retainer at different loads

由图18、19和图21可知,随着负载增大,各接触副接触载荷成正比增加,同时初始的冲击增大,导致曲线初始波动随之增大。齿轮副与其他接触副不同,如图20所示,初始波动依然较小,且接触载荷随着负载增大而减小。由3.1节分析结果可知,螺纹副和保持架是主要承载零件,也就是说随着负载增加螺纹副和保持架共同分担了齿轮副部分载荷,使得齿轮副接触载荷变小。因此,各接触副的动态接触载荷应根据使用载荷工况的变化进行详细计算。

3.4 摩擦系数对啮合副动态接触特性的影响

保持载荷和转速条件不变,设置摩擦系数分别为0.01、0.02、0.03、0.1、0.2,分析不同摩擦系数对动态接触特性的影响规律。滚柱-丝杠侧和滚柱-螺母侧动态接触载荷、齿轮副动态接触载荷、滚柱轴端与保持架动态接触载荷的影响规律如图22～25所示。

图22 不同摩擦系数下滚柱-丝杠侧动态接触载荷Fig.22 Dynamic contact load at the roller-screw interface at different friction coefficients

图23 不同摩擦系数下滚柱-螺母侧动态接触载荷Fig.23 Dynamic contact load at the roller-nut interface at different friction coefficients

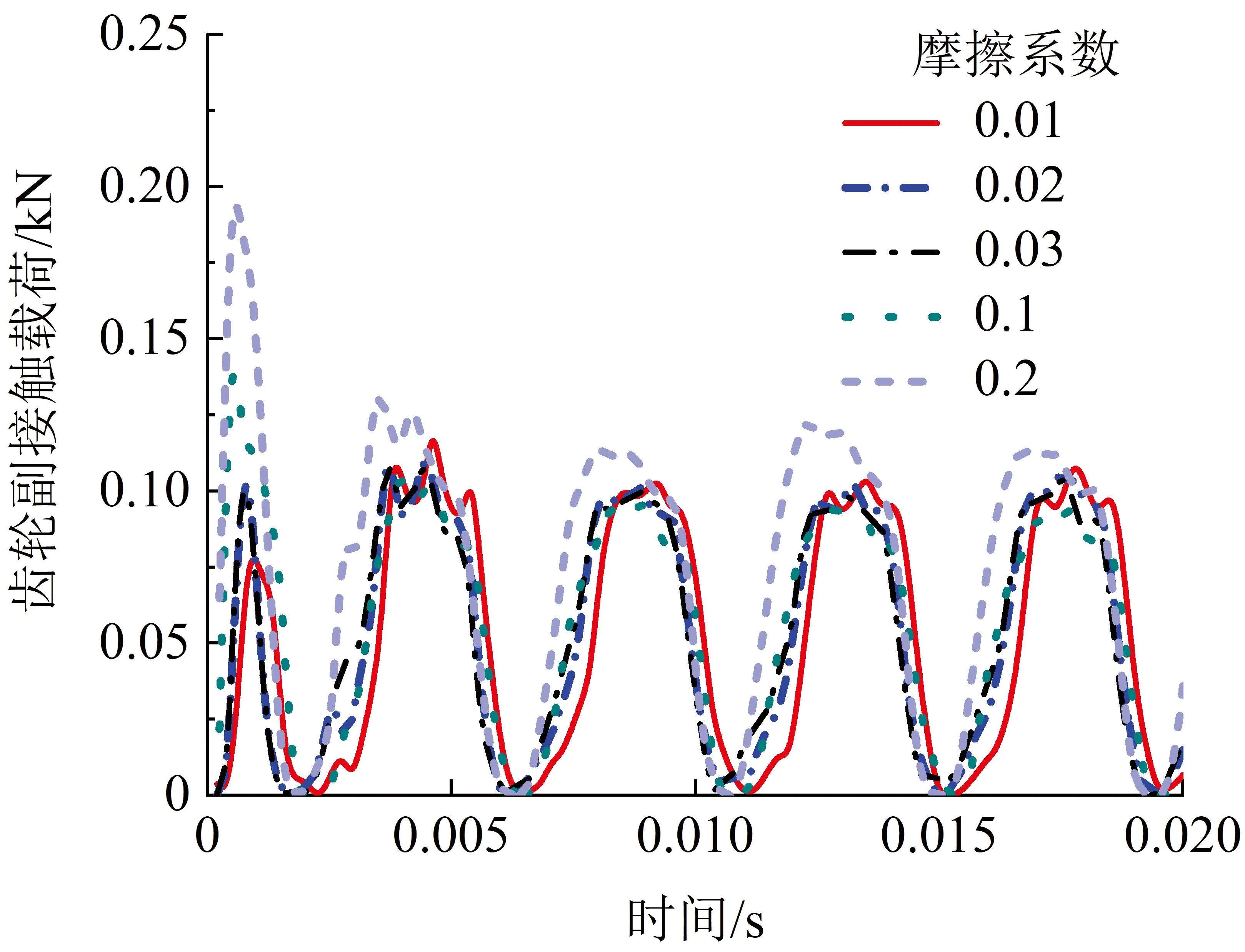
图24 不同摩擦系数下齿轮副动态接触载荷Fig.24 Dynamic contact load at the gear pair at different friction coefficients

图25 不同摩擦系数下滚柱轴端-保持架侧动态接触载荷Fig.25 Dynamic contact load at the roller-retainer at different friction coefficients

如图22～25所示,当摩擦系数为0.01～0.03时,各接触副的接触载荷较小且变化不大,当摩擦系数为0.1、0.2时增幅较大,稳态阶段各接触副的接触载荷同样增幅明显,尤其是初始阶段接触载荷曲线波动变大。可见,较大的摩擦系数是导致各接触副接触载荷产生剧烈波动的主要原因之一,为提高PRSM运转可靠性和稳定性,应尽可能减小摩擦系数。