采用改进灰狼算法的移动机器人路径规划
2022-11-02刘志强何丽袁亮张恒
刘志强,何丽,袁亮,张恒
(1.新疆大学机械工程学院,830047,乌鲁木齐; 2.北京化工大学信息科学与技术学院,100029,北京)
移动机器人路径规划直接关系到机器人的行进效率。路径寻优算法是路径规划的核心,依据理论的不同,移动机器人路径规划技术可分为基于采样的图搜索算法、基于节点的搜索算法、基于模型的方法、基于生物启发式算法等方法[1]。粒子群算法(PSO)[2]、蚁群算法[3]、萤火虫算法[4]等都是典型的生物启发式算法,较传统规划算法,减少了对数学模型的依赖,全局寻优能力强,在移动机人路径规划研究中已经得到大量的实际应用。
灰狼优化(grey wolf optimization,GWO)[5]算法作为一种新型的生物启发式算法,具有结构简单、需要设置的参数少和在实验编码中易实现等优点,近年来在调度[6]、无人机路径规划[7]、图像处理[8]、模型参数优化[9-10]、移动机器人路径规划[11]等领域广泛应用。然而,在移动机器人的路径规划问题实际求解中,传统GWO算法存在固有缺陷,如初始种群缺乏多样性、全局勘探与局部开发不平衡、易陷入局部极值等,会影响到机器人的运动效率,增加碰撞风险。刘二辉等[12]在求解自动导引小车路径规划问题中,基于GWO算法引入启发式初始解生成算法,改善了灰狼初始种群质量差的缺陷;同时,提出了基于邻域搜索的启发式算子,避免了算法陷入局部停滞,但增加了GWO算法的计算复杂度,缺乏考虑全局搜索与局部搜索间的平衡关系。针对这些GWO算法固有问题,研究者们先后提出了诸多改进策略,大体分为以下3类。
(1)初始化种群策略。传统GWO算法采取随机设定的方式,生成初始阶段的灰狼种群,导致初始灰狼种群缺乏多样性,限制了算法搜索灵活性。张铸等[13]采用混沌映射方法来随机、遍历、规律地生成多样的初始种群;伍铁斌等[14]采用佳点集方法,设定灰狼个体的初始位置,以保证个体尽可能均匀地分布在搜索空间中;韩驰等[15]采用反向学习方法生成初始灰狼种群,确保GWO算法尽可能利用解空间信息。
(2)修改控制参数策略。在GWO算法中,系数向量V和H是两个至关重要的控制参数,直接影响算法全局勘探搜索与局部精确开发的平衡,其中,V由收敛因子a决定,先后有很多研究者们通过非线性调整a来修正V。为提升算法全局搜索能力:Mittal 等[16]引入指数衰减函数来非线性调整参数a;柳长安等[17]提出余弦函数型调整策略,拟合参数a实际变化过程,得到了较好的平衡效果。在关于控制参数H的调整中:Rodríguez等[18]提出一种基于自适应的参数H调整策略,有利于动态更新搜索范围,能够有效提高灰狼勘探能力;龙文等[19]结合随机向量动态调整参数H,能够有效平衡GWO算法的全局搜索与局部开采能力。
(3)修改位置更新公式。传统GWO算法后期,个体趋近于头狼所在最优区域,缺乏个体自主搜索,易陷入局部早熟收敛。为此,先后有研究者提出位置更新公式修改策略。Long 等[20]提出差分进化策略生成新个体,使得个体位置分布多样化,避免了GWO算法陷入局部收敛;Rodríguez等[21]在传统灰狼个体位置更新公式的基础上,先后引入静态加权平均、基于适应度划分比例权重等策略,提高了算法搜索效率;受粒子群算法位置更新思想启发,滕志军等[22]将个体所遍历的最佳位置与群体中最优值相结合来更新下一代灰狼个体位置,提高了全局寻优性能。
虽然诸多GWO算法改进策略对算法性能有所提升,但收敛性效率低、全局勘探与局部搜索不协调、易陷入早熟停滞等固有问题仍然存在。现有的研究大多缺乏对这些固有缺陷的统筹改进,导致收敛效果提升不明显,算法综合性能缺乏稳健性。为此,本文提出一种多策略融合的改进灰狼优化算法(TGWO),其主要工作是:采用Tent混沌映射初始化策略,生成灰狼起始位置序列以增加初始种群位置分布的多样性;引入指数型非线性约束改进收敛因子,同时融合收敛因子调整控制狼群勘探能力的参数H,以平衡算法全局与局部搜索能力;提出融合动态权重因子和适应度比例权重系数的位置更新策略,以避免算法陷入局部收敛。最后:通过标准函数对比测试实验,证明了TGWO算法寻优速度更快、精度更高;选用障碍物分布方式不同的环境,分别展开全局路径规划仿真对比实验,验证了本文所提改进策略的有效性。所提改进策略一定程度上提高了灰狼优化算法在移动机器人全局路径规划问题求解过程中对不同复杂度环境的适应性以及路径寻优结果的稳定性,从而实现了移动机器人全局自主移动路径最优,提升了静态避障效果及导航效率。
1 GWO算法
灰狼优化算法[5]作为一种典型的生物启发式算法,是对灰狼群体中社会等级分层、群体捕食猎物这两种行为的模拟、优化。灰狼的社会等级有领头狼α、副领头狼β、普通狼δ、底层狼ω共4个层级,并且层级越低狼的数量越多。灰狼的群体捕猎活动在领头狼α的决策与领导下有序开展,捕食行为先后有追捕、包围和最后攻击共3个阶段。其中,围捕猎物这一过程的数学模型表示为
X(I+1)=Xp(I)-V|HXp(I)-X(I)|
(1)

(2)
式中:X、Xp分别为灰狼个体、猎物的位置向量;I为目前的迭代次数;V、H为系数向量;r1、r2分别为[0,1]间的随机向量;a为收敛因子,迭代过程中由2线性减小到0,即

(3)
其中Imax为最大迭代次数。
狼群最终攻击目标猎物,可用数学模型表示为
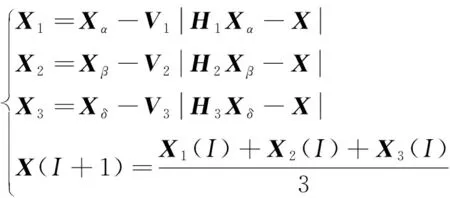
(4)
式中:Xα、Xβ、Xδ为α、β、δ的位置向量;V1、V2、V3、H1、H2、H3计算方式同式(2)。
2 TGWO算法
2.1 Tent混沌映射

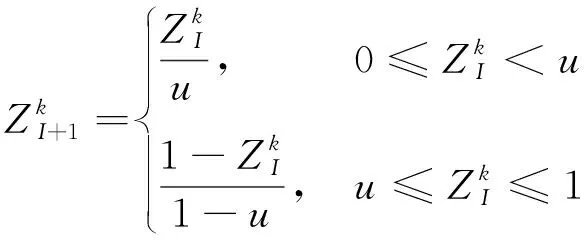
(5)
式中:k为种群数;为保持算法初始化信息的随机性,u⊂rand(0,1)。

(6)

2.2 控制参数调整
平衡GWO算法的全局搜索与局部搜索过程对于发挥其优化性能尤为关键。狼群在包围猎物时,如式(1)所示,系数向量V、H是控制狼群搜索范围的关键参数。V表示狼群的搜索半径,用于分阶段调整狼群与猎物间距。同时,控制参数H也协调着GWO算法全局勘探与局部开采能力。
2.2.1 指数型收敛因子a策略
GWO算法的实际寻优过程中,搜寻范围需要非线性动态调整,线性收敛因子a所决定搜索半径V的变化不能客观、完整体现实际搜索过程。为此,本文提出一种指数型的收敛因子a更新策略,以更好地拟合GWO算法中收敛因子a实际的非线性变化过程。a更新公式为

(7)
式中:as=2、ae=0分别表示收敛因子起始、终止值;λ1,λ2∈(0,1)分别为非线性调节系数。
由式(7)可得,在迭代过程中,指数型调整策略可动态调整收敛因子a的非线性变化,更新搜索半径V,更准确地拟合GWO算法的实际全局与局部搜索过程。
2.2.2 控制参数H调整策略
在GWO算法中,参数H同样决定着灰狼与猎物的靠近程度[19]。为进一步平衡算法的全局与局部搜索,提出改进策略
H=2r3-a
(8)
式中:a由式(7)所得;r3为[1,1.5]内的随机向量。
由式(8)可知,控制参数H的调整策略是引入改进过后的指数型收敛因子a,在拟合狼群实际搜索过程的基础上,进一步调节参数H。在搜索前期,满足|H|<1,能够提升狼群全局勘探能力,丰富狼群位置分布的多样性;在搜索后期,满足|H|>1,能够增强GWO算法局部开采能力,准确锁定全域最优值,提高收敛速度。随机向量r3的引入同样增加狼群搜索位置的遍历性。
2.3 改进位置更新公式
传统GWO算法中:由式(1)可得,第I代狼群围捕猎物时,假定猎物位置保持不变[5],这与现实环境中猎物位置实时的移动状况不符;由式(4)可得,底层灰狼个体位置更新时,采取跟随策略缩小与头狼最优位置差距,从而接近目标猎物,缺乏对灰狼个体自主搜索的考虑;实际位置更新计算时,对适应度值排前3的α、β、δ头狼先验位置采取均等贡献率计算,等级区分不够显著。这些固有问题限制了GWO算法的勘探寻优效率,甚至在一些复杂环境中极易陷入局部收敛,难以找到全局最优解,为此本文提出以下位置更新公式修改策略。
2.3.1 动态权重因子
文献[24]中,为平衡粒子群优化算法(PSO)局部搜索与全局搜索能力,采用惯性权重系数w调整策略,公式为

(9)
式中:wmax、wmin分别表示最大和最小惯性权重值;m为目前迭代次数;M为最大迭代次数。
受其启发,引入动态权重因子b,动态更新灰狼个体步长,公式为
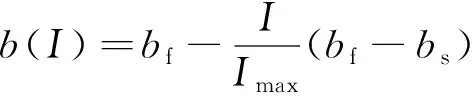
(10)
式中bs、bf分别表示权重因子的初值与终值。
2.3.2 适应度比例系数
为有效区分头狼α、β、δ的不同引导作用,在原始静态平均的基础上,引入适应度比例系数,动态加权平均以区分头狼贡献率,引导后续灰狼个体位置更新。适应度比例系数计算如下:
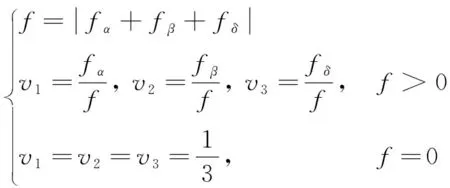
(11)
式中:v1、v2、v3为适应度比例系数;fα、fβ、fδ分别为α、β、δ的适应度值。
2.3.3 融合改进的位置更新公式
融合改进的位置更新公式为
X(I+1)=b(I)r4(v1X1+v2X2+v1X3)
(12)
式中:r4为[0,1]间的随机向量;b(I)由式(10)计算;v1、v2、v3由式(11)计算。
在新的位置更新公式(式(12))中:首先,引入呈线性递减变化的动态权重因子,综合考虑狼群捕猎实际过程中,猎物位置移动的多变性以及灰狼个体位置更新的自主性,动态调整步长更新,更好地开发GWO算法的搜索寻优能力;其次,引入适应度比例系数,根据不同适应度,权衡α、β、δ头狼对后续灰狼个体位置更新的不同引导作用,更有利于后续的底层灰狼个体趋近于全局最优解来更新位置。新的位置更新公式能够有效地拟合灰狼个体实际位置更新过程,提升算法在全域搜索的遍历性,以防止陷入局部范围的早熟停滞。
2.4 TGWO算法流程
步骤1输入:种群规模N,搜索维度d,非线性调节系数λ1、λ2,最大迭代次数Imax。
步骤2初始化:灰狼个体α、β、δ的适应度值空间f(Xα)、f(Xβ)、f(Xδ),位置空间Xα、Xβ、Xδ。
步骤3基于Tent混沌映射形成初始种群{Xi},其中,i=1,2,3,...,N。
步骤4计算灰狼个体适应度值f(Xi),并进行排序,其中,i=1,2,3,...,N。
步骤5将适应度值排名位于第1、2、3的灰狼个体记为α、β、δ,并记录其位置信息Xα、Xβ、Xδ。
步骤6分别根据式(7)更新收敛因子a,相应得出搜索半径V。根据式(8)更新H,根据式(10)更新动态权重因子b。
步骤7依据2.3.3小节所述的融合改进位置更新公式策略,先后由式(10)~(12)更新狼群个体位置。
步骤8如果I 基于图幅为Nx×Ny二维栅格,模拟实际机器人移动环境[3],如图1所示。设定每个栅格的边长为1,黑色栅格为障碍物所占据的区域,空白栅格为移动机器人允许越过区域,以左上角为原点,第i个栅格位置坐标描述为(xi,yi)。 图1 10×10栅格示意Fig.1 10×10 grid diagram 实际的路径寻优过程中,设定每只灰狼个体捕猎时更新形成的位置坐标集合代表机器人的一条移动路径,TGWO算法通过优化策略,从诸多路径集合中寻找一条符合约束条件的最优路径。约束条件如下。 (1)路径连续性条件。移动路径不能有迂回状况,假设机器人由当前节点(x1,y1)移动到下一节点(x2,y2)应至少满足x2>x1或y2>y1。 (2)环境边界与障碍物约束条件。移动路径必须限定在固定图幅边界的栅格区域内,且移动路径节点及节点间的连线禁止穿过障碍物栅格。 (3)目标路径最短条件。在满足约束条件(1)、(2)下的诸多栅格位置中,第j(j=1,2,3,...,Ny)行栅格应选横坐标最小值i(1 (13) 式中:n为路径节点数;D为栅格边长。 TGWO算法性能验证实验包括标准函数测试实验和移动机器人全局路径规划仿真实验两部分。仿真实验平台为一台2.59 GHz、16 GB内存、Intel(R) Core(TM) i7-9750HF CPU、Windows 10操作系统的计算机,软件平台为MATLAB R2018a。 仿真实验中的算法参数设置见表1。为了实验的客观性与准确性,最大迭代次数Imax、种群规模N、搜索维度d参照对比算法所在原文献,并结合路径规划应用中对比算法实际所需搜索空间统一设置;TGWO算法的非线性收敛系数λ1、λ2和权重因子初值、终值bs、bf由多组标准函数测试实验及路径规划仿真实验取得。 表1 仿真实验中的算法参数设置 4.1.1 测试实验基础设置 为了测试TGWO算法的性能,同时验证改进策略的优越性,将TGWO算法与传统GWO算法[5]和另外3种改进灰狼算法进行标准函数测试对比实验,包括PSO-GWO算法[22]、CGWO算法[13]、LIL-GWO算法[19]。5种对比算法的参数设置如表1所示,测试实验中选取文献[25]中8个通用的标准测试函数,详细信息如表2所示,其中:单峰函数F1~F4可用来测试算法的局部搜索、开发能力;多峰函数F5~F8可用来测试算法的收敛性、算法全局勘探与局部开发的平衡能力[19]。5种对比算法分别测试运行30次。 表2 标准测试函数相关信息 4.1.2 测试实验结果分析 不同算法在标准测试函数上的平均值、标准差、迭代收敛数和综合这3项指标的Friedman检验排名[26]如表3所示。可以看出:相较于GWO算法、PSO-GWO算法、CGWO算法,TGWO 算法在函数F1、F2、F4、F6、F8上测试结果所取得的平均值更优,但是TGWO算法在函数F3上所取得的平均值排名落后;就单峰函数F1~F4以及多峰函数F8上测试结果所取得的标准差来看,TGWO算法的标准差要更小,优于GWO算法、PSO-GWO算法、CGWO算法;相较于LIL-GWO算法,TGWO算法在函数F1、F2、F5、F7上的平均值、标准差取得相同的优化结果,在函数F4、F6上,TGWO优于LIL-GWO;TGWO算法相比其他4种算法,在函数F1~F5、F7、F8上趋于全局最优解时的迭代数,最终Friedman检验排名处于最优。由此可见,TGWO算法的收敛性能更强,寻优精度更高,且寻优结果更稳定,鲁棒性更强。 4.1.3 收敛曲线对比分析 5种算法基于测试函数的收敛曲线如图2所示,分析可得以下结论。 (a)F1 表3 基于标准测试函数的5种算法测试对比结果 (1)从图2(a)~(d)可以看出,TGWO算法相较于其他4种算法,寻优效果更理想。这主要归因于改进的位置更新公式策略引入了动态权重因子和适应度比例系数。在搜索过程中,F4曲线表明,TGWO算法能有效避免局部收敛和局部停滞现象;F1曲线表明,TGWO算法可保持较快的收敛速度,表现出更强的局部的开发能力。 (2)从图2(e)~(h)可以看出,TGWO算法相较于其他4种算法:在搜索前期收敛曲线呈快速下降状态,表明采用Tent混沌映射以初始化种群的策略能够有效提升算法迭代初期的收敛速率;在搜索的中后期,TGWO算法能更准确地锁定全局最优解。F6曲线表明,在初次找到最优解时,LIL-GWO算法就停止继续搜索,而TGWO算法会继续保持搜索开发过程,并很快锁定更优的结果。这得益于TGWO算法采用指数型收敛因子策略以及改进控制参数H策略,能够协调算法的全局勘探与局部开发过程。 为进一步验证TGWO算法在一般室内静态模拟环境下的全局路径规划问题求解中的寻优性能,进行本小节仿真实验。首先,基于15×15栅格的环境1(模拟不规则障碍物稀疏分布的小型室内场景),开展TGWO算法各个改进策略相较于原始GWO算法在路径长度、寻优效率等优化性能具体提升效果的消融实验验证;接着,基于20×20栅格的环境2(模拟障碍物规则分布的中型室内场景)、50×50栅格的环境3(模拟障碍物密集且随机分布的大型室内场景),开展TGWO算法与3种典型的改进灰狼算法在路径规划综合寻优能力的对比验证实验。 4.2.1 消融实验结果分析 消融实验的5种对比算法分别是TGWO算法、原始GWO算法以及3种单一策略改进的灰狼算法。3种单一策略改进的灰狼算法分别是TGWO1(基于Tent映射策略)、TGWO2(基于控制参数改进策略)、TGWO3(改进位置更新公式)。TGWO2的非线性调节系数λ1、λ2,TGWO3的权重因子初值与终值bs、bf设置见表1,实验次数为30。消融实验结果如图3和表4所示。 从图3可以看出,传统GWO算法存在路径寻优收敛速度慢、对全局最优路径搜索能力不足、先后会有多次陷入局部极值导致搜索停滞、多次实验所得最优路径值不稳定等问题。TGWO1算法在迭代 (a)最优路径 前期收敛速度更快,但相较于其他改进策略,仍存在较长阶段的局部收敛现象,直至第364代才收敛于全局最优路径;TGWO2算法除了进一步提升了初始阶段全局搜索时的收敛速度外,还进一步协调了搜索中后期对局部的开发,在第85代就锁定了全局最优路径;TGWO3算法在搜索前期第65代就可以跳出局部极值找到全局最优路径,有效缩短了算法的局部停滞;融合各个改进策略优势形成的TGWO算法有效改善了传统GWO算法在优化上存在的不足,提高了算法的整体收敛性能与搜索性能。 表4 环境1中30次实验的算法性能对比 从表4得出:相较于传统GWO算法,融合改进的TGWO算法以及逐一改进后的TGWO1、TGWO2、TGWO3算法,平均路径长度更短且结果更稳定,平均迭代数更少,算法的收敛速度得到提升,并由此缩短了寻优耗时。 4.2.2 算法对比实验结果分析 4种对比算法分别为TGWO、PSO-GWO[22]、CGWO[13]、LIL-GWO[19],参数设置见表1,实验次数为30。实验结果如图4、图5、表5、表6所示。 (a)最优路径 (a)最优路径 图4(a)和图5(a)表明,TGWO算法相对于其他3种算法,在规则地图(环境2)和离散地图(环境3)下都有较强的搜索、避障能力,能够有效减少路径转折次数,寻找得到的平均路径值48.60和127.83都是最短长度,这是因为融合改进的个体位置更新公式策略增强了算法路径寻优的准确性。图4(b)和图5(b)表明,TGWO算法收敛曲线较其他3种算法的收敛曲线,分别在迭代前期的第41代和第15代就可准确、快速地锁定全局最优路径,这是因为TGWO算法所采用的种群初始化改进策略使得个体初始位置分布多样性增加,收敛速率得到提升。TGWO算法所采用的控制参数调整策略能够有效平衡路径寻优的全局与局部搜索能力。 由表5和表6可知,TGWO算法的平均路径、路径长度标准差、平均迭代数、平均寻优耗时相较其他3种改进GWO算法,都呈现一定的优势。由此可见,TGWO算法在路径规划问题中,综合寻优能力更强,具有更好的收敛性和鲁棒性。 表5 环境2中30次实验的算法性能对比 表6 环境3中30次实验的算法性能对比 本文提出一种改进的灰狼算法TGWO,以求解移动机器人全局路径规划问题,结合标准测试函数验证结果和全局路径规划仿真实验结果,得出以下结论。 (1)针对传统GWO算法初始种群分布不均的缺陷,本文TGWO算法引入Tent混沌映射以均匀地初始化灰狼种群,加快了算法在路径寻优初始阶段的收敛速度。针对传统GWO算法全局搜索与局部开发不协调问题,本文TGWO算法提出控制参数调整策略,一定程度提高了算法在路径寻优过程中的避障能力和综合勘探能力。针对传统GWO算法极易陷入局部最优的问题,本文TGWO算法采用融合策略更新底层灰狼个体位置,使得算法在路径寻优最后阶段能较为准确地锁定全局最优解。 (2)标准函数测试实验表明,与传统GWO算法、3种改进GWO算法相比,TGWO算法具有较好的收敛效果和寻优精度,本文所提改进策略有效。 (3)全局路径规划仿真实验表明,在复杂度不同的3组仿真实验场景下,TGWO算法计算所得的路径有效、合理。相对比于传统GWO算法、3种改进GWO算法,本文TGWO算法在路径寻优能力、收敛效率、寻优结果稳定性、环境适应能力等方面具有一定的优越性。 (4)本文提出的TGWO算法相较于传统非生物启发式算法具有结构简单、计算复杂度较小、全局搜索能力较强等优势。本文所提的各项改进策略可为其他启发式群智能算法的优化改进以求解全局路径规划问题提供参考。 (5)后续,将进一步优化TGWO算法的寻路搜索方式,并与曲线处理策略结合。在确保路径寻优精度的基础上,进一步提高路径的平滑性,适应更多特定的复杂曲折地形环境。此外,TGWO算法还可以与局部动态避障方法相结合,提高移动机器人的导航效率和稳定性。3 基于TGWO算法的路径规划
3.1 环境模型的建立
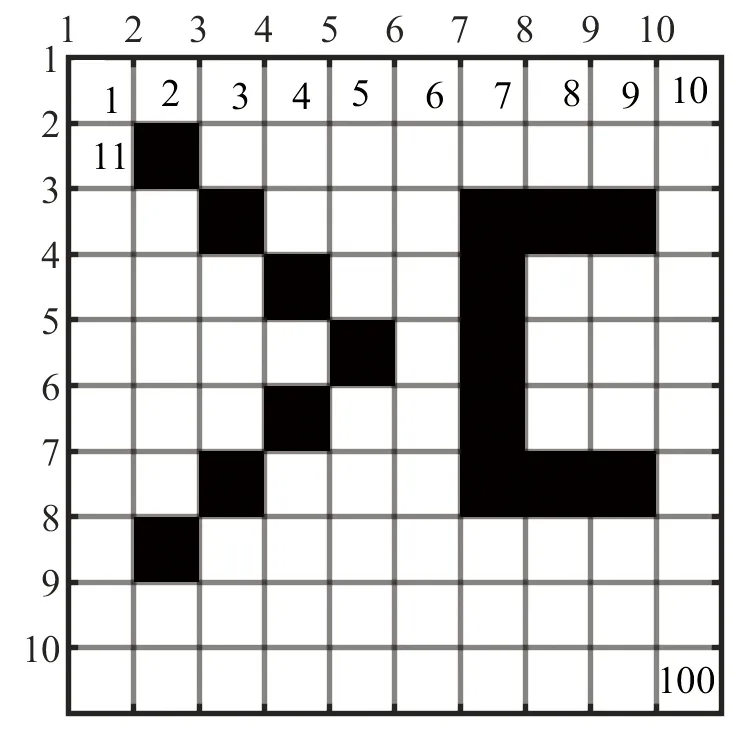
3.2 路径寻优约束条件与适应度函数

4 仿真实验结果与分析
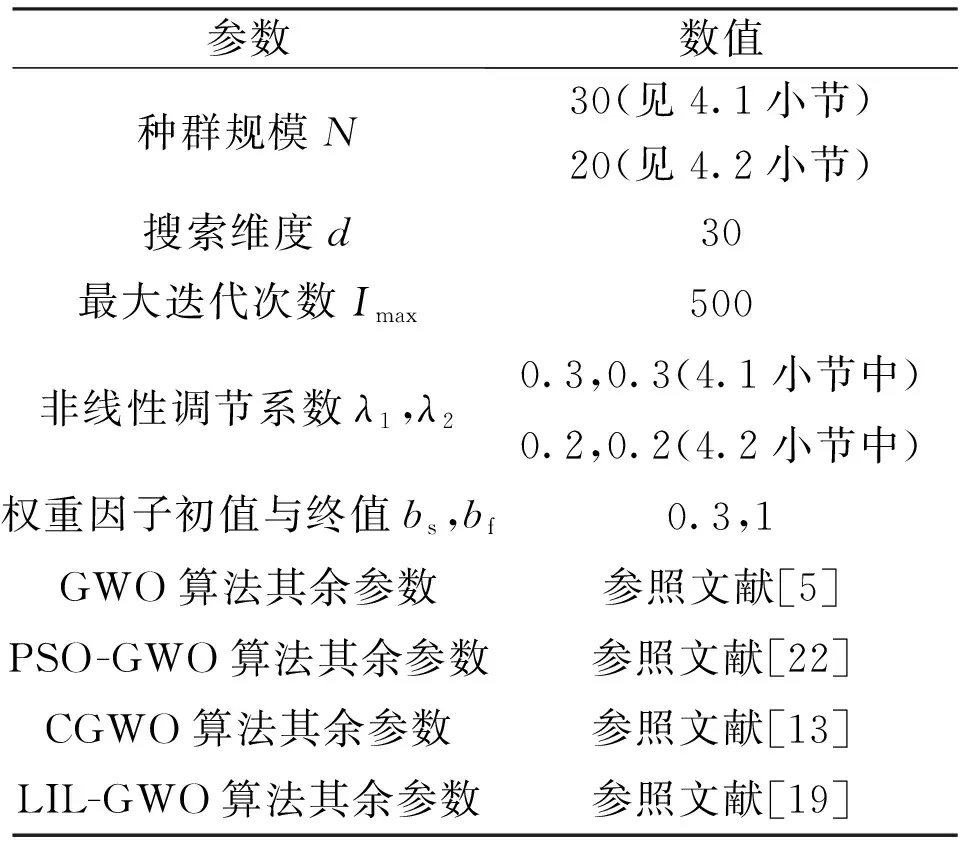
4.1 标准测试函数实验


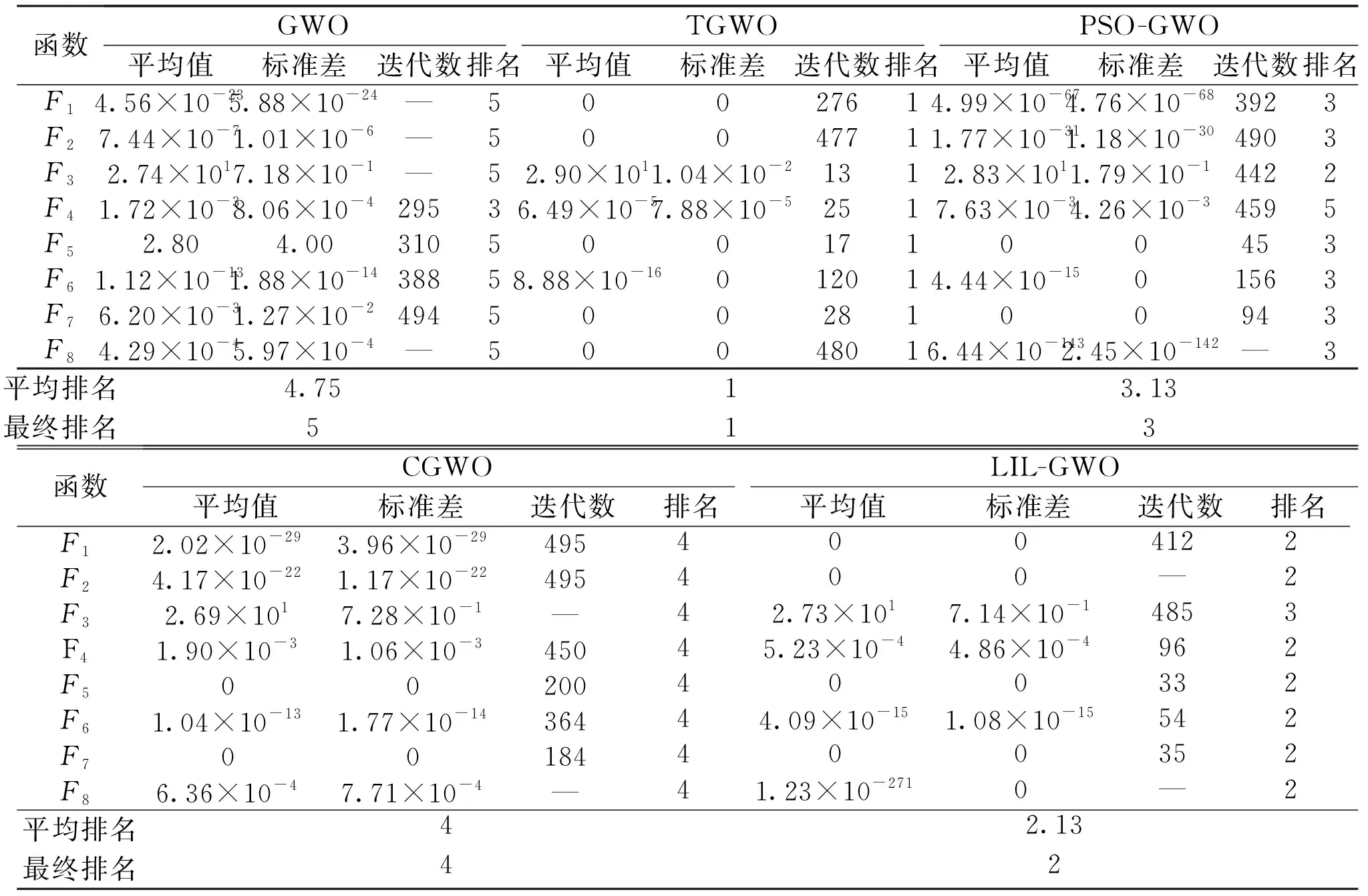
4.2 路径规划仿真
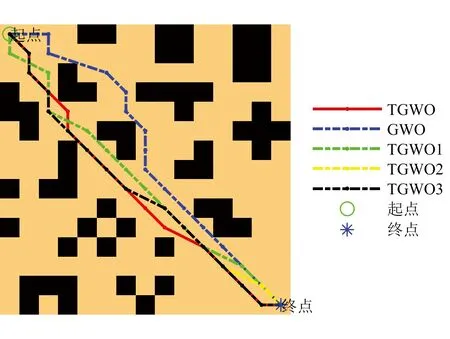





5 结 论
