动生涡流无损检测的二维稳态解析模型

邓康轩,冯 搏,康宜华

(华中科技大学机械科学与工程学院，湖北武汉 430074)

0 引言

随着经济的发展，市场对铝板带材的需求量越来越大，对铝材的要求也向着更薄的方向发展。为了增大铝带板材的产量，轧机的速度越来越快，最高可达20～25 m/s[1]以上，在生产过程中易产生缺陷，但常规无损检测方法难以对铝带的缺陷进行高速检测。

T. J. Rocha等[2]提出动生涡流的方法来实现金属导体的高速检测，动生涡流传感器包括永磁铁和磁敏元件。永磁体和导体试件之间因为存在相对运动而在导体试件中产生动生涡流，当导体试件中存在缺陷时，会对涡流产生扰动，并被磁敏元件拾取。动生涡流强度随导体运动速度的增大而增大，因此适用于高速检测。B. FENG等[3-4]也利用动生涡流探头对金属材料进行了检测，并对比了铁磁性金属与非铁磁性金属检测信号的特征。F. YUAN等[5]采用直流线圈代替永磁铁作为激励源，进一步研究动生涡流对导体试件中缺陷的检测效果，提出了一种定量表征运动铁磁性材料裂纹的方法。但目前研究主要集中在动生涡流检测缺陷的实验和仿真，并没有相应的解析模型。解析模型能够让研究人员对机理有更加深入的理解[6]，是传感器优化的基础[7]，因此，本文将对动生涡流无损检测方法的解析模型进行研究。

在涡流检测及脉冲涡流检测中，研究人员对解析模型进行了大量研究。C.V. Dodd等[8]已经给出了轴对称和非轴对称单频涡流管道检测的频域解析解。T. Theodoulidis等[9-10]在Dodd-Deeds模型的基础上将电磁场和涡流线圈阻抗的积分表达式用级数展开代替，减少了计算时间，更好地控制了收敛性。M. B. FAN等[11]利用电磁场的反射和透射理论，建立了层状平面导体上方同轴激励感应探头的解析模型。张卿、武新军等[12]基于罗宾边界条件，建立了脉冲涡流的解析模型。

本文在上述研究的基础上，建立了基于导线激励的动生涡流检测解析模型。首先基于Maxwell方程组分别推导出空气和导体中电磁场的控制方程，然后引入Fourier变换求得解析模型的频域通解，再根据磁场垂直和平行边界条件，求解得到空间中磁场的分布以及导体试件中涡流的分布。最后将解析结果和有限元结果对比，验证解析模型的正确性，并基于解析模型对检测速度的影响进行了分析。

1 基于导线激励的动生涡流检测模型

本文拟对动生涡流检测的二维解析模型进行研究，并建立稳态时的涡流分布。动生涡流检测基本原理如图1所示，磁铁与被测导体试件之间以相对速度v运动，从而使试件中产生涡流。

图1 动生涡流检测模型

图2 导线激励等效的动生涡流检测解析模型

2 动生涡流的稳态解析解

2.1 解析模型的控制方程

列出Maxwell方程组的微分形式，如式(1)。

(1)

式中：B为磁感应强度，T；E为电场强度，V/m；J为电流密度，A/m2；D为电位移矢量，C/m2；ρ为电荷密度，C/m2；μ为磁导率，H/m。

根据电磁场在运动坐标系中的伽利略变换和欧姆定律，当金属导体以速度v运动时，其电流密度为：

J=σE+σν×B

(2)

式中σ为金属薄板的电导率，S/m。

将式(2)代入式(1)中，并在等式两边同时取旋度，可得

(3)

根据矢量恒等式

(4)

及式(1)，有

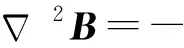
(5)

将式(5)代入式(3),得

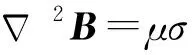
(6)

根据矢量运算，有

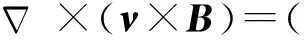
(7)

代入式(6)，得

(8)

将式(1)和式(8)代入式(6)中，得

(9)

式中νx和νy分别为速度ν在水平和垂直方向上的分量。

在动生涡流检测中，激励为直流磁场，因此磁场对时间的导数为0。并且如图2所示的模型中，导体只存在x方向的水平运动，因此式(9)可化简为：

(10)

式(10)即为电磁场在导体试件中的控制方程。

同理可得在空气中的控制方程

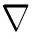
(11)

将矢量形式的控制方程在笛卡尔坐标系下展开可得磁场x和y分量在空气和导体中的控制方程。在空气中：

(12)

式中Bx、By分别为磁感应强度B在水平和垂直方向上的分量。

在导体试件中：

(13)

2.2 解析模型的频域通解

为对磁场进行求解，引入Fourier变换与逆变换，分别如式(14)、式(15)。

(14)

(15)

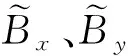
式(15)是将空间域函数表示为空间频域函数的积分形式，将式(15)代入(12)可得空气中磁场的频域方程：

(16)

解得空气中磁感应强度的频域通解为：

(17)

式中Cx、Dx、Cy、Dy为通解中的参数。

将式(15)代入(13)可得导体中磁场的频域方程：

(18)

式中k′2=k2+jkμσvx

解得导体试件中磁感应强度的频域通解为：

(19)

2.3 解析模型的边界条件及求解

为对多匝导线激励情况进行计算，先计算只有单匝导线的情况。最后对单匝导线的解进行积分，即可求得多匝导线的情况。

将空间划分为Ⅰ、Ⅱ、Ⅲ、Ⅳ4个区域，如图3所示，并建立如图所示的坐标系，由式(16)、式(18)分别写出4个区域的通解。因为在区域Ⅰ中，当y→+∞时，磁感应强度有界，所以区域Ⅰ中的Cx和Cy为零。在区域Ⅳ中，当y→-∞时，磁感应强度有界，所以区域Ⅳ中的Dx和Dy为零。所以区域Ⅰ中磁场频域通解为：

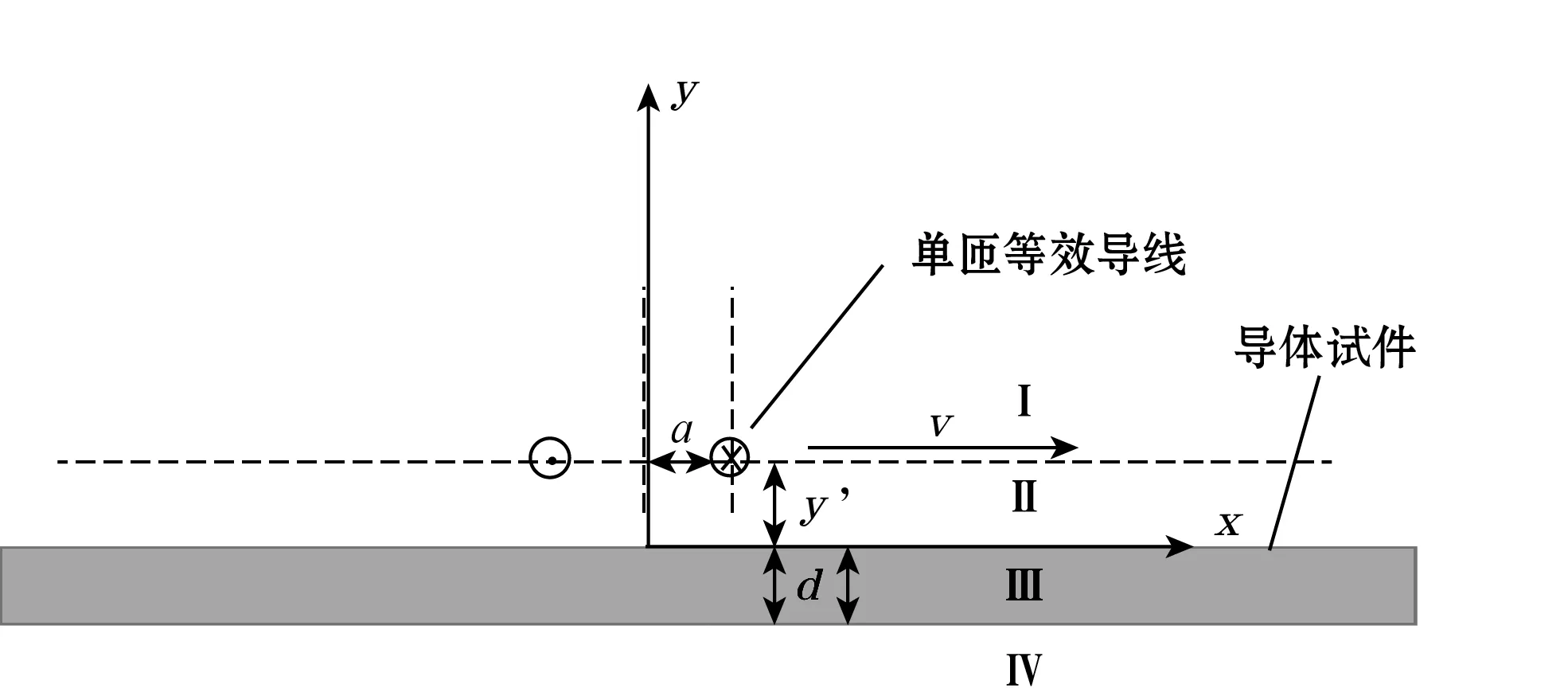
图3 单匝导线模型示意图

(20)

区域Ⅱ中磁场频域通解为：

(21)

区域Ⅲ中磁场频域通解为：

(22)

区域Ⅳ中磁场频域通解为：

(23)

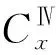
由磁场的垂直分量连续分别得到在y=y′，0，-d处的边界条件

(24)

(25)

(26)

由磁场的平行分量连续分别得到在y=0,-d,y′处的边界条件：

当y=0，-d时

(27)

(28)

当y=y′时

式中：I为等效导线中电流；δ(x)为狄拉克δ函数。

等式两边同时做Fourier变换：

积分后得：

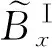
(29)

又由式(1)，得：

在区域Ⅰ中，有：

(30)

在区域Ⅱ中，有：

(31)

(32)

在区域Ⅲ中，有：

(33)

(34)

在区域Ⅳ中，有：

(35)

由式(24)～式(35) 组成的方程组可解得各系数，这里主要研究的是导体试件的涡流分布，只写出区域Ⅲ的系数。

(36)

(37)

(38)

(39)

又根据式(1)可得

(40)

式中Jz为电流密度在z方向上的分量。

由式(36)、式(15)可得：

(41)

对于多匝导线，导体中产生的涡流即为单匝导线的结果沿y′方向上从y0到y0+h的积分，即

(42)

然后做Fourier逆变换

(43)

即可得到导体中稳态涡流场的解析模型。

3 有限元仿真验证

为了对解析模型进行验证，现将有限元和解析模型计算结果进行对比。导体试件选取的材料为铝材，在解析模型中给定各个参数的值，令a=0.005 m，y0=0.005 m，h=0.01 m，v=-5 m/s，d=0.005 m，μ=4π×10-7H/m，I=6×105A，σ=3.53×107S/m。并给定需要绘制的涡流密度图像的导体试件的范围，令x=-0.04～0.04 m，y=-0.005～0 m，代入稳态涡流场的解析模型，理论计算出导体试件中各点的涡流密度的值，在MATLAB中作出图像，如图4所示。

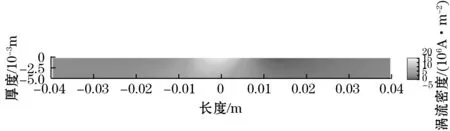
图4 理论计算的导体试件中的涡流分布图

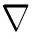
图5 ANSYS仿真计算的导体试件中的涡流分布图

为了更好地对比涡流分布，用命令流提取导体试件中的涡流密度大小，导入MATLAB进行绘图，得到结果如图6所示。

图6 ANSYS仿真计算在MATLAB中的表示

对比图4和图6，可以看出解析结果与有限元结果基本一致。

分别提取有限元仿真和解析模型计算得到的导体试件上表面的涡流密度的值，得到的结果如图7所示。从图7中可以看出有限元仿真和解析模型计算得到的导体试件上表面的涡流密度基本相等。

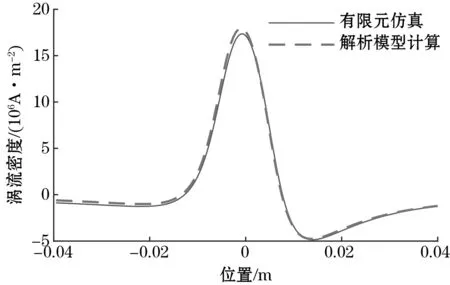
图7 有限元仿真和解析模型计算得到的导体试件上表面的涡流密度的值

4 基于解析模型的导体运动速度影响分析

相比于有限元模型，解析模型能更方便、快速地对动生涡流检测中的影响参数进行分析。基于本文得到的解析模型，可以研究导体运动速度对涡流分布的影响，对解析模型中的速度v取不同的值后(1～6 m/s)代入计算，用MATLAB作出不同速度下导体试件中的涡流分布图，如图8所示。可见，动生涡流密度随导体运动速度的增大而增大，并且导体试件中产生的涡流产生拖尾效应也随导体运动速度的增大而变得更加明显。

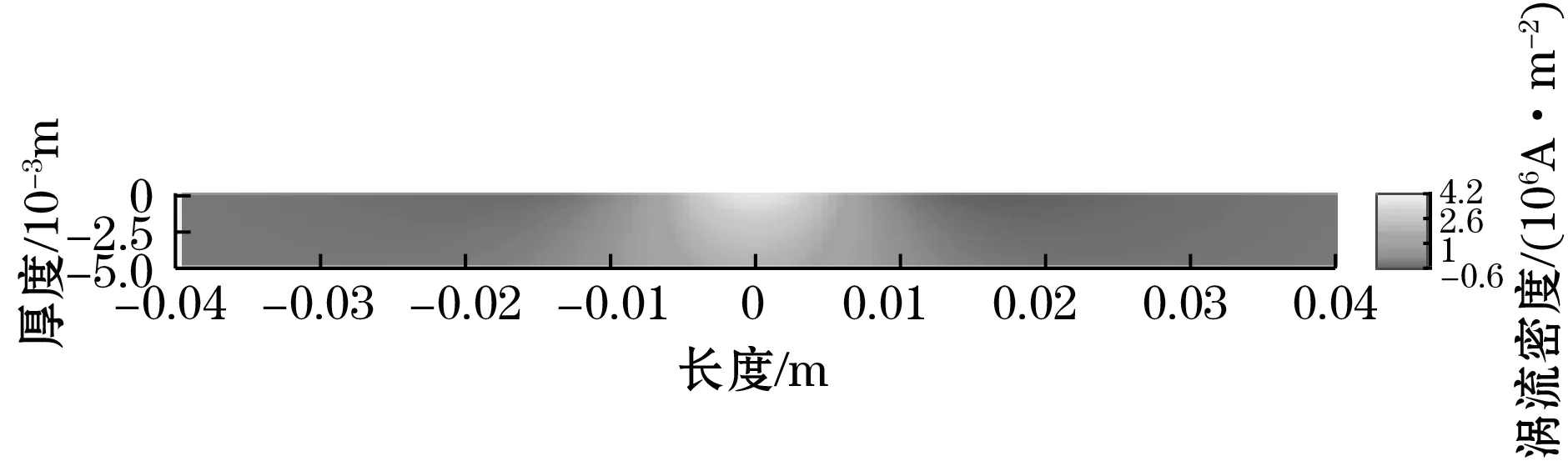
(a)v=1 m/s

(b)v=2 m/s

(c)v=3 m/s

(d)v=4 m/s

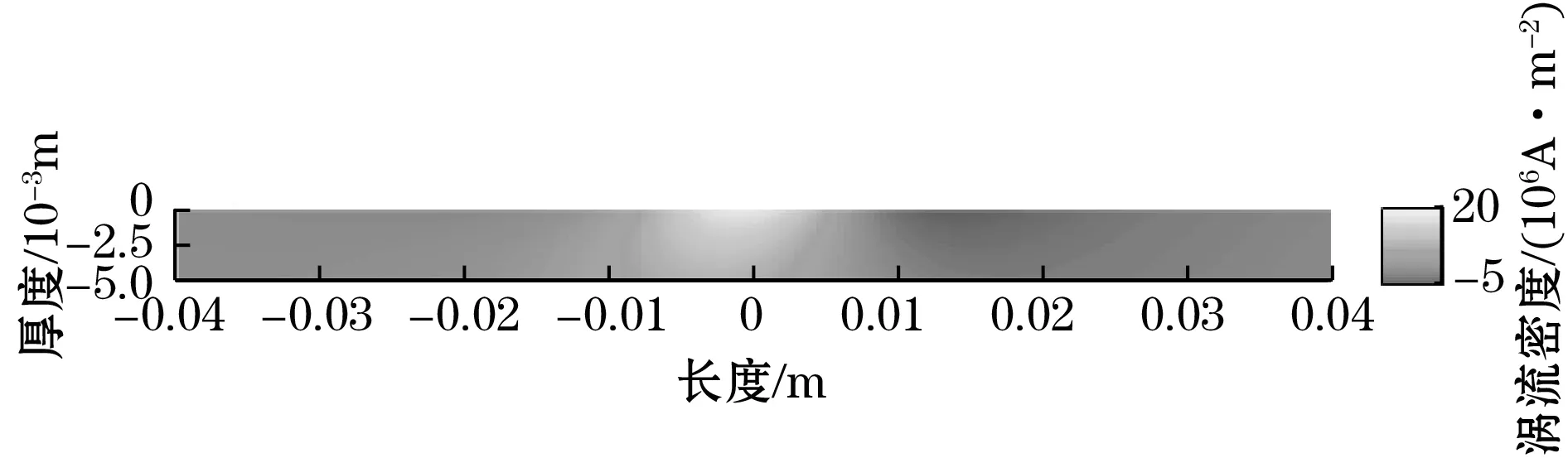
(e)v=5 m/s

(f)v=6 m/s图8 不同速度下导体试件中的涡流分布图

提取导体试件上表面的涡流密度的值，如图9所示。从图中也可以看出，导体运动速度越快，导体试件中涡流密度越大。

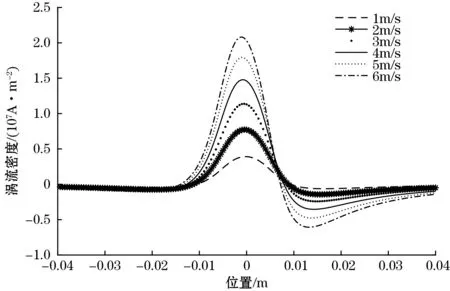
图9 不同速度下导体试件上表面的涡流密度的值

5 结论

本文应用Fourier变换建立了基于导线激励的动生涡流检测解析模型。利用该检测模型可以计算出导体试件内的涡流密度，得到导体试件中涡流的分布情况。通过与ANSYS仿真结果进行对比，对该模型进行了验证。最后基于解析模型计算发现，导线运动速度越快，导体试件中的涡流密度越大。该解析模型可用于分析导体运动速度、传感器尺寸、提离等因素对动生涡流检测的影响。在后续研究中，将继续对动生涡流的三维稳态模型及暂态模型进行研究。