等效采样与移动拟合结合的超声测厚方法

王选择，张瑜灿，王爱辉，翟中生，冯 维，王浩伟

(1.湖北工业大学机械工程学院，湖北武汉 430068；2.湖北省现代制造质量工程重点实验室，湖北武汉 430068； 3.中国特种飞行器研究所结构腐蚀防护与控制航天科技重点实验室，湖北荆门 448035)

0 引言

超声波穿透能力强，应用于金属测厚，具有成本低、速度快、精度高的特点[1]。对航空航天与核工业等恶劣环境或高风险领域中所使用压力容器、工艺装置等的结构和部件，采用超声波进行壁厚测量是适时可行的[2],它为部件在使用寿命内能否可靠运行的判断提供了有效的依据[3-4]。

超声波的频率较高，一般测厚使用超声探头频率在0.5～15 MHz之间，在超声测厚中，对其超声信号不失真的采集，其采样频率为50 MHz以上，才能满足高时间分辨率测量的要求，且对超声波信号采集速度越快，每个采样点所代表的时间精度越高，相应所表示的范围越精细，对测量系统也提出了很高的要求。目前超声测厚系统一般需要专门高速AD采样芯片与FPGA控制器[5]，系统复杂。另外，超声测厚的准确性依赖于超声测厚中的渡越时间[6](time of flight，TOF)，即超声回波信号周期提取的准确性，传统峰值法测定回波信号周期，通过测量相邻超声回波信号中峰峰值的时间差作为渡越时间[7]，峰值法容易受到噪声的干扰，致使回波信号中的峰值出现偏移，其渡越时间的估计误差较大。

针对上述问题，本文提出等效时间采样与FFT粗估、移动正弦拟合算法精确提取相位的超声测厚处理方法，解决了采集超声回波信号需要高频采样的局限性与传统通过峰值点位置特征直接计算工件厚度精度低、稳定性差的缺陷等问题。仅使用STM32F407微处理器，利用其内部低频AD采样功能以及开发的移动正弦拟合算法，实现了超声测厚的目的，提高了超声测厚系统的性价比。

1 改进的等效采样技术

等效采样技术作为一种针对重复性信号的有效采样方法[8]，在宽带取样数字示波器[9]以及高速采样仪器设备等方面应用广泛，它为构建测量信号的完整性[10]提供了可行性。

等效采样的实质是通过对低频采样信号的重构与合成，达到高频采样的效果。能够进行等效采样的信号一般满足2个前提条件:被采集信号具有周期性，该信号的周期是已知的。

1.1 常规的等效采样技术

等效采样可分为顺序等效采样[11]和随机等效采样[12-13]。

顺序等效采样是一种常用的等效采样方法，基本原理是按固定次序对待测周期信号进行采样，当采样点的数量达到要求后，顺序地将采样点重新组合，重构待测信号。如图1所示，5个周期内采集到5个点，重构后合成1个周期内5个采样点。

图1 顺序等效采样原理示意图

随机采样的基本原理如图2所示，数据采集系统每次触发时，均形成一组采样序列点，每组所采样的第1个点相对于触发信号是随机的，利用其随机间隔Δt大小依次排序各组采样数据，重构待测信号[14]。

图2 随机等效采样原理示意图

顺序等效采样方案原理简单，通过产生固定的微小延时步进，实现等效采样频率，但由于每周期仅采样一个点，遍历完整波形所需时间很长。随机等效采样需进行多组内插采集并排序重构，其难点在于随机时间间隔Δt的测量，目前基于TAC时间间隔测量技术应用较广泛[15]，但采样硬件系统构造较复杂、实现成本较高。

1.2 适于超声测厚的等效采样改进方法

超声测厚系统的信号采集号也可以采用等效采样方法，等效地提高采样频率。主要是在测量过程中，一方面通过超声探头按照一定的频率进行周期性激励，相应地产生周期性的超声回波信号，另一方面对超声回波信号按照某个设定频率进行顺序采样。它是对常规顺序采样中单周期仅采样一个点的方案的改进，具有更高的采样效率。

1.2.1 激励频率与采样频率的设定方法

超声测厚系统采用等效采样的关键在于超声探头激励频率与回波信号采样频率的设置。

超声探头的激励频率fx决定了超声信号的周期，每个信号周期内含有多个超声回波信号。假设信号的采样频率设定为fs，为了达到等效采样的目的，设计fx与fs满足如下关系：

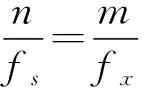
(1)

式中：m、n为正整数，即n个采样点时间与m个信号周期时间相等，且n与m互质。

也就是采样频率满足fs=n·fx/m，通过周期合成后，n个点合成到1个周期内，那么等效采样频率为

Fse=nfx=mfs

(2)

相当于采样频率提高了m倍，保证了低频采样系统能够获得高频的采样结果。m、n、Ts、Tx需要根据系统时钟进行合理设置。

1.2.2 超声信号的重构复原方法

由于等效采样需要把多个信号周期内的采样点合成到一个信号周期内，因此需要对信号进行重构排序。

图3中包含多个逐步衰减的超声回波信号超声激励周期为Tx=1/fx，这里它也被作为一个信号周期。由于采样周期Ts=1/fs，则m·Tx=n·Ts，如前所述，m个激励周期内正好包含n个采样点。

图3 超声回波信号等效采样原理示意图

m与n互质能保证n个采样点不重复地均匀插入到一个周期内，合成一个完整的信号周期，这里称之为采样重构。

重构方法如下：假设采样序列信号为x(r)，重构序列为y(r*)满足：

y(r*)=x(r)

(3)

r为采样点序列号从0到n-1，r*为重构信号的序列号，按照如下公式计算：

(4)

式中：m为信号周期数；n为采样点数；[ ]表示向下取整符号。

由于采样的随机性，周期性的激励信号难以做到与采样的同步，因此重构序列与原始回波信号相比较，初始点位置产生了平移。根据回波峰值特征，通过确立最大点位置后，再进行简单平移，就能得到与原始回波信号一致的回波序列。如图4所示，利用超声回波信号逐渐衰减特征性，通过最大值位置的特征平移算法，对信号进行重组恢复，有效地复原了激励周期内的超声回波信号，保证超声回波信号的准确性。

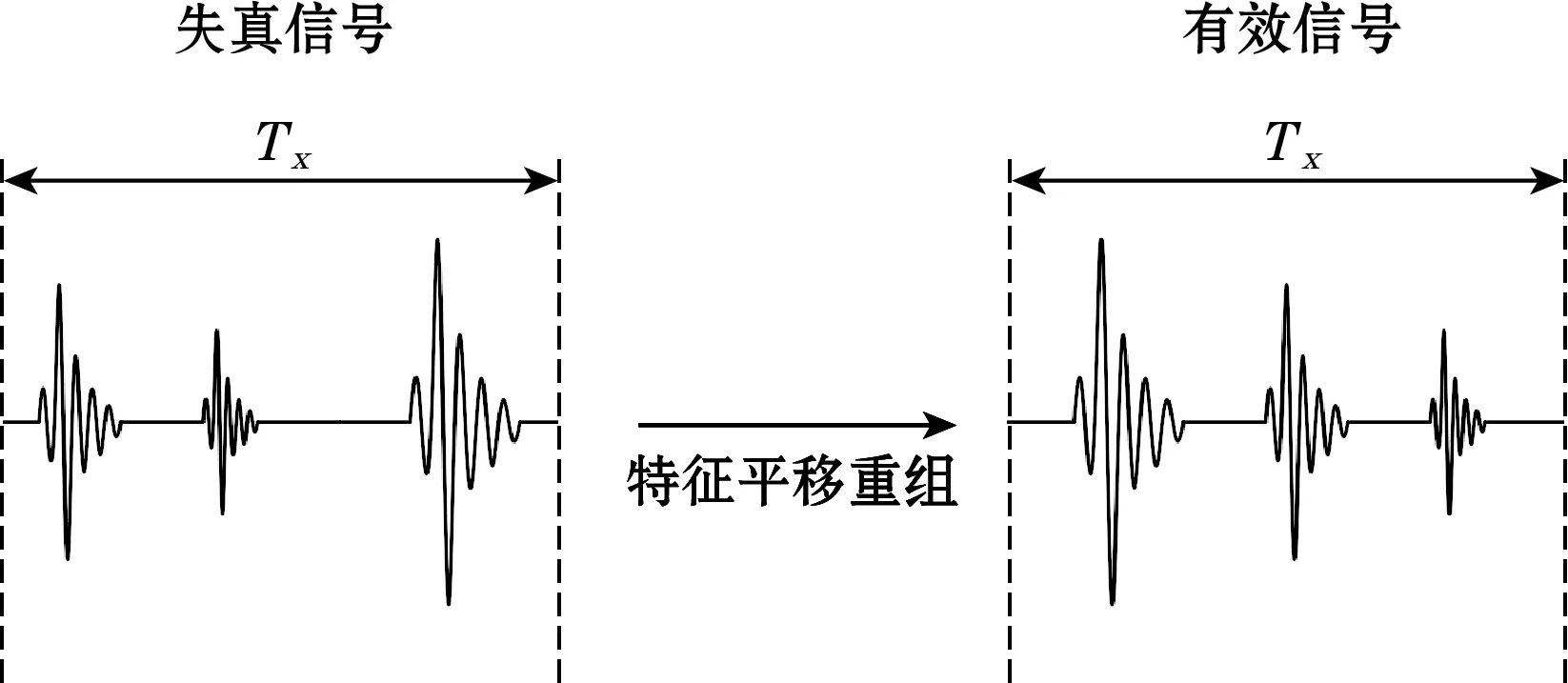
图4 超声回波信号复原示意图

显然，通过简单设定采样频率与激励频率之间的关系，使得改进的等效采样相对于原来的方法更加简单、快速有效。

2 超声波测厚系统设计

2.1 硬件系统的设计

超声测厚的硬件主要由超声激励电路、超声波探头，模拟乘法器电路，AD采集电路以及STM32F407微处理器组成。超声激励电路主要控制高压脉冲触发超声波探头，使其发射超声波信号，从而对工件进行测厚。模拟乘法器电路利用AD835乘法器芯片对超声回波信号进行自乘处理，把交变的超声信号变成脉动直流信号，便于低频AD芯片采集。信号处理主要是STM32F407微处理器对采集的信号进行重构，恢复高频超声回波信号，以及运用FFT粗估与移动正弦拟合算法精确提取相位信息，从而得到回波信号周期ΔT，标定声速后，得出其工件厚度。图5为超声测厚整体设计框图，图6为超声测厚系统实物图，图7为上位机通讯显示界面。

图5 超声测厚整体设计框图

图6 超声测厚系统实物图

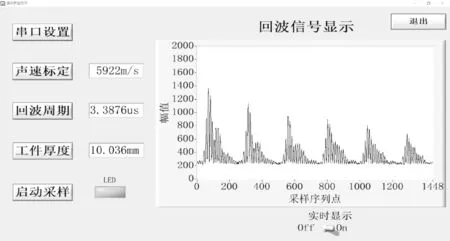
图7 上位机通讯显示界面

2.2 模拟乘法器的作用

由于超声回波信号中夹杂着幅值变化的更高频信号，具有平滑滤波性质的低频采样器直接采样将导致信号很大的衰减，显著降低了采样信号的信噪比。

分析超声测厚中，实际采样所需要的仅是回波信号中有用的包络信息，因此，在采样之前，利用模拟乘法器对超声信号进行自乘，可以得到低频采样不易衰减的大于零的单值回波包络信号。

图8、图9为原始超声回波与自乘后的超声回波仿真信号，原始回波信号经平滑滤波衰减到原来的1/5，而自乘后的回波信号经平滑滤波衰减到原来的1/2。因此自乘后的回波信号更适合低频采样转换器件的采集处理。

图8 原始回波仿真信号

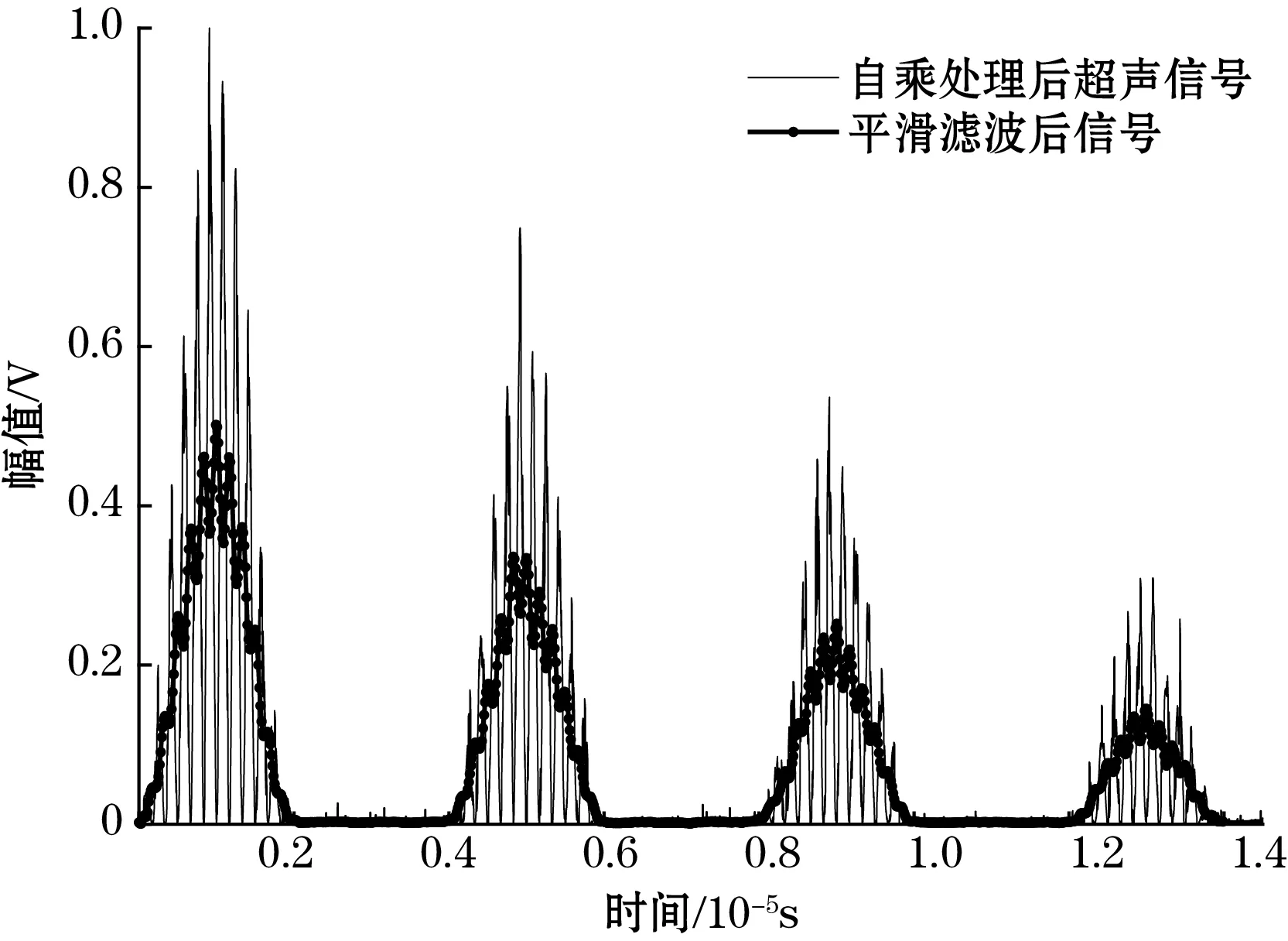
图9 自乘后的超声回波仿真信号

2.3 软件程序流程设计

基于STM32F4核心的超声测厚系统软件设计流程如图10所示。通过内部定时器按照设定的频率，生成占空比很小的PWM信号控制高压驱动器，产生周期性的高压激励脉冲，驱动超声探头工作。

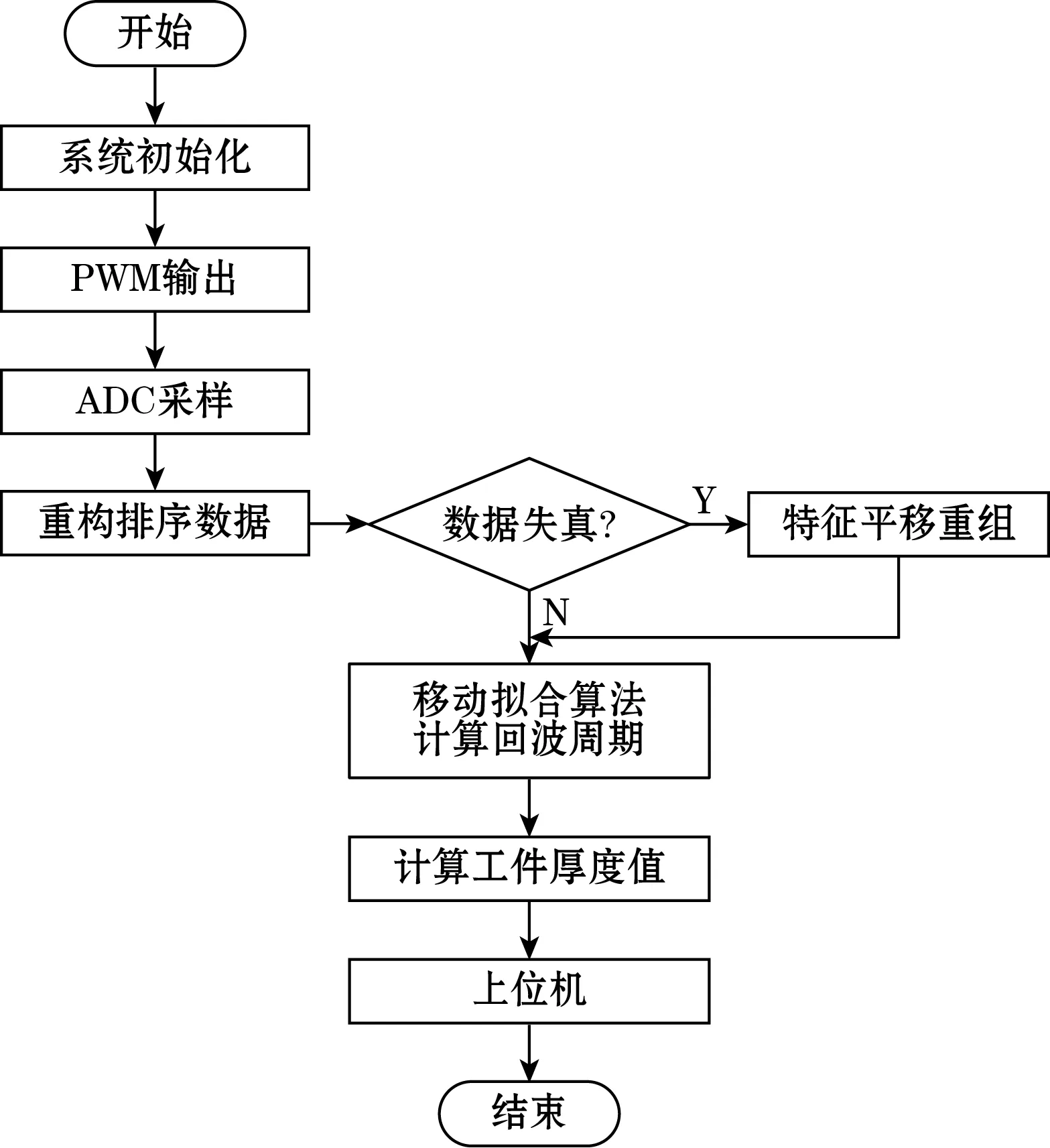
图10 系统程序流程图

采集数据时，单片机内部的ADC转换模块按照设定采样频率进行数据采集。一旦采集完后，进行重构排序与平移复原，得到重构的超声回波序列。

利用移动正弦拟合算法对回波序列进行处理，准确计算回波信号周期，从而得到工件厚度值，最后将结果发送至上位机。

3 超声回波时间差计算的信号处理方法

超声回波测厚的关键在于准确计算2次回波信号之间的时间差，由于回波信号的高频、衰减特性以及受噪声干扰的影响，很容易导致计算上出现较大误差。

3.1 最大峰值法

图11为采集的重构的超声回波信号，A1、A2是被测工件的回波信号，根据脉冲回波法原理，通常选取回波信号中最大峰值作为特征值，并把相邻特征值之间的时间差作为回波时间差，进一步计算被测工件的厚度值[16]。

图11 峰值位置偏移回波信号

实际测量中，由于干扰噪声的影响，超声回波信号的最大峰值位置产生了偏差，所识别的最大峰值不能保证为所需要的特征值。也就是导致回波信号中峰值特征值不能稳定准确提取，厚度测量出现较大误差。

如图11所示，理论上在第1次回波A1取P1峰值，对应在A2取P2峰值，与实际上A1与A2处识别的最大峰值为P1、Q2位置，这样超声回波信号时间差得不到准确提取，工件的厚度也就难以准确测量。

为此，考虑到峰值点位置特征直接计算工件厚度精度低、稳定性差的缺点，提出一种基于线性移动正弦拟合的包络相位特征提取回波周期的方法，进行稳定的高精度厚度测量。

3.2 移动正弦拟合提取相位方法

由于这里采用线性正弦拟合需要知道被拟合序列的相位间隔，因此采用FFT算法粗估超声回波的基频谐波，并根据该基频谐波大小计算相位间隔。

3.2.1 粗估回波周期的方法

对于幅值衰减的超声回波重构序列，选取有效的回波段信号，假设N个点，经过FFT运算后，通过极大值点的判断与选取，可以找到回波基频谐波对应的频率点位置k。考虑到超声信号直流分量的影响，选取次极大值点作为回波基频谐波频率稳定可靠。根据该频率点位置，粗估回波序列相位间隔，即：

(5)

3.2.2 移动正弦拟合包络相位的计算方法

除一个周期的边界损失外，逐段的移动正弦拟合可以得到采样序列点上的各点幅值与相位信息[17]。

超声回波信号虽然不是标准的正弦信号，但其幅值衰减变化的特点非常适合采用移动正弦拟合进行处理。移动正弦拟合的实质是获取回波信号中基频谐波的各点幅值与相位。

若超声回波序列为y(i)，段长为l的第q段序列表达为{y(q)，y(q+1)，…，y(q+l-1)}，对其正弦拟合，可以得到该段序列的幅值A(q)与初相位φ(q)分别为：

(6)

式中aq、bq计算如下：

(7)

矩阵Q0为一常数对称矩阵：

(8)

根据正弦信号周期对称性的特点，对整周期采样点数的拟合具有更高的精度。因此，逐段移动正弦拟合采用的段长应尽量接近超声波回波信号的周期长度，这里可以根据式(5)计算的间隔相位，设计拟合的段长为

(9)

移动正弦拟合的计算量较大，如果对式(7)中的累加和运算采用递推方式可以极大降低计算量[17]。

考虑到式(6)中所求的初相位序列φ(q)为包裹相位，可以通过解包裹运算得到解包裹相位[18]为φ(q)。

对数据集[q，φ(q)]进行最小二乘的线性拟合，即满足如下公式：

φ(q)=s1q+s0

(10)

在直线拟合计算拟合的斜率参数s1之后，精估超声回波信号时间差为

(11)

工件厚度为

(12)

式中vs为超声波传播速度。

4 测厚实验与分析

4.1 系统参数设置

设置单片机STM32F407微处理器系统时钟频率144 MHz，作为基准时钟频率。设置处理器自带ADC模块的采样时钟频率36 MHz的条件下，其最小采样转换周期Tmin=15/36 μs。实际采样转换周期应满足Ts>Tmin。

单脉冲激励周期Tx与采样周期Ts分别由内部定时器触发，且根据系统时钟合理设置激励定时计数器的累加值R1=36 000，采样定时器累加值R2=86，则超声激励周期Tx=R1/144 μs=250 μs。采样周期Ts=R2/144 μs=43/72 μs。其中，受采样转换时间的限制，R2要求大于60，设置R2=86满足要求。

利用等效采样公式(1),可知采样点数n、采样周期数m与计数器累加器R1、R2设置值满足如下关系：

m·R1=n·R2

(13)

在满足等效采样n、m互质前提下，设置m=43，进而计算出n=18 000，相应的采样时间为t=43×250 μs=10.75 ms。

根据前面的推导，此时实际的采样频率fs=144/86 MHz=72/43 MHz,等效采样频率为fse=72 MHz，采样频率提高了43倍，实现对高频超声回波信号不失真的采样。

4.2 信号的采样与重构

对10.03 mm的试块进行超声波测厚试验。如图12所示为对超声回波信号进行ADC采样，得到的连续43次激励的超声回波采样信号。

图12 等效采样信号

按照前面提到的超声信号的重构复原方法对采样信号进行重新排序，得到重构的回波信号，形成一个激励周期内的完整回波信号。如图13所示：显示了重构信号起始的2 500个点的序列图。

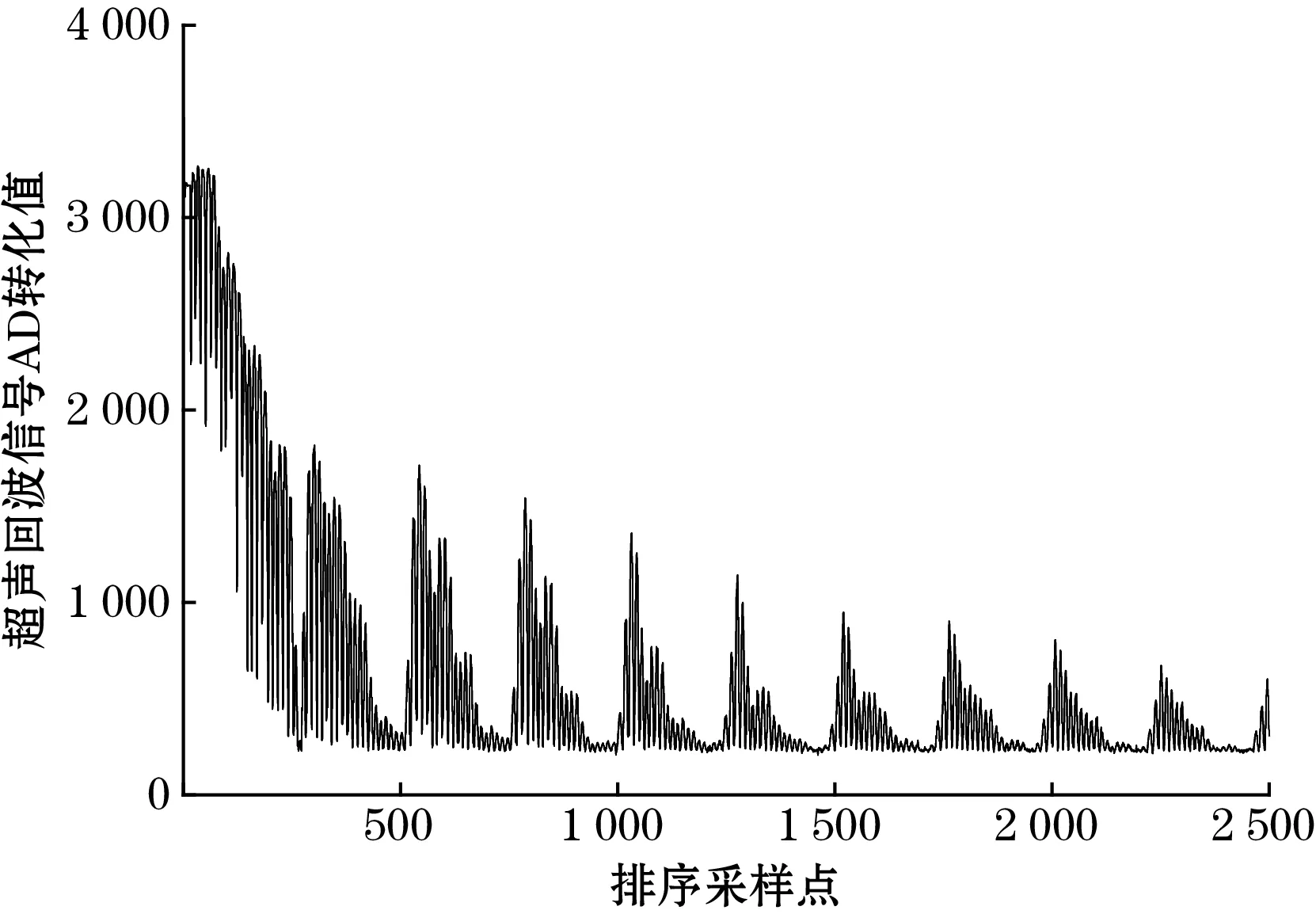
图13 重构超声回波信号

4.3 回波时间差的提取

按照移动正弦拟合提取相位的方法计算回波时间差。粗估回波信号谐波频率的基频，选取N=4 096点的重构序列，进行FFT变换如图14所示。

图14 FFT频谱图

得到次极大值对应的频率点位置k=18-1=17，按照式(5)确定相位间隔δ=0.026 rad，由式(9)确定回波信号移动正弦拟合段长l=241。

在确定δ、l之后，通过式(6)、式(7)的移动正弦拟合算法，计算重构回波信号的有效采样点对应的相位φ(q)。有效采样点数目一般是段长l的10倍以内，考虑实际回波信号的衰减情况，这里取9l的数据量。拟合边界损失后，剩下8l个包裹相位信息，然后对相位解包裹，如图15所示。根据式(10)进行线性回归计算得斜率s1=2.576×10-2。

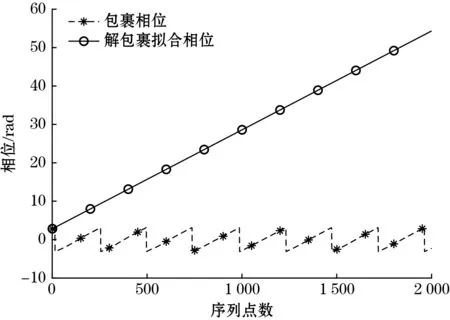
图15 超声回波相位图

最后，已知Tx=250 μs、n=18 000，根据式(11)，计算回波时间差：

4.4 测量结果与分析

4.4.1 声速的标定测量

对已知厚度值为5.71、10.03、19.94 mm的超声波阶梯试块(1018钢)分别进行连续15次重复性测量，测得的回波时间差的均值为1.925 8、3.387 5、6.732 0 μs。如图16所示。应用线性回归，得到厚度H与Te之间的线性相关参数。

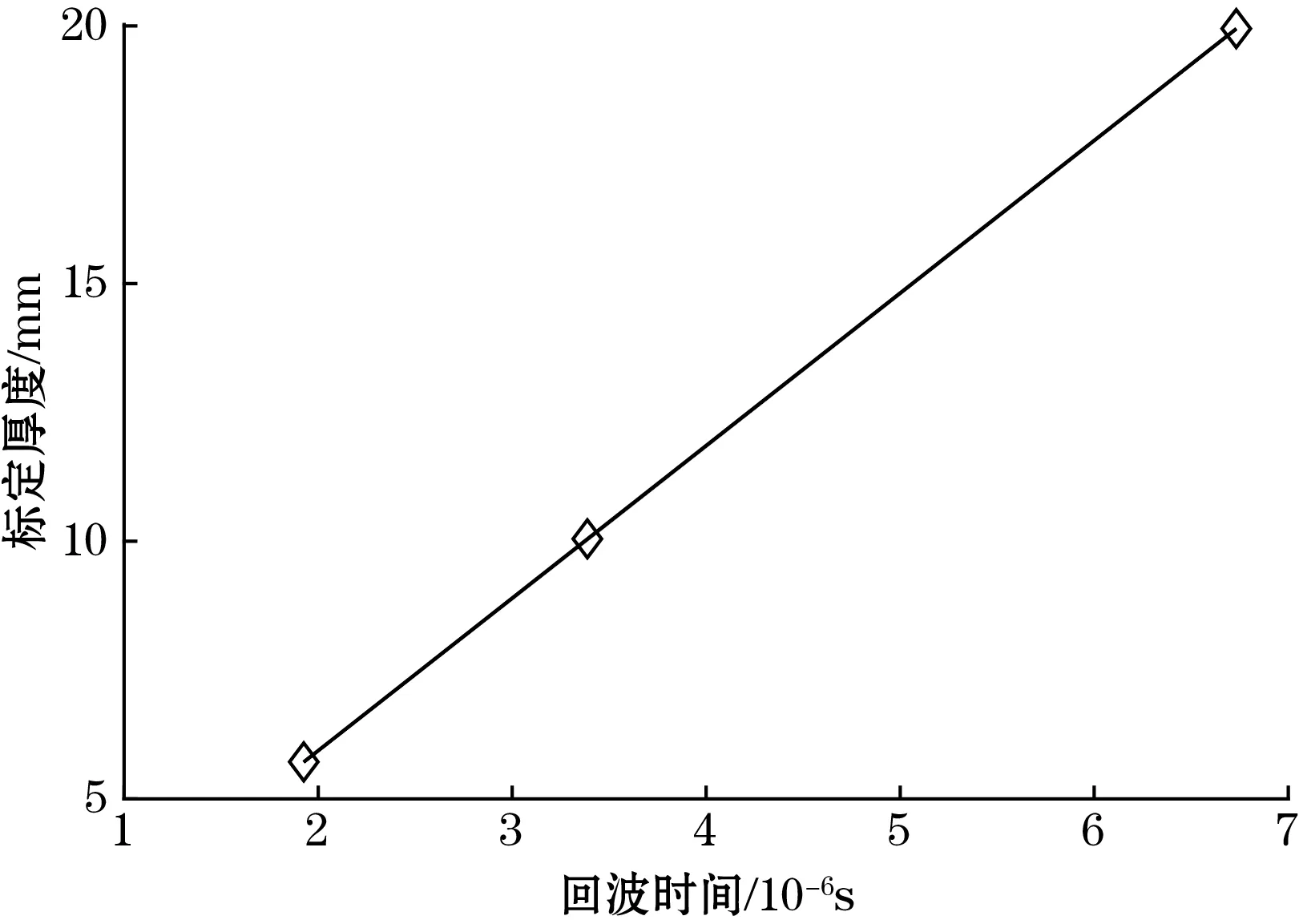
图16 1018钢的回归方程

根据线性回归的参数，可以计算1018钢的超声传播速度[1]，可得1018钢的标定声速为5 922 m/s，零位校准值为0.004 mm。

已知常用声速表中钢的声速为5 900 m/s，二者比较接近，验证了测厚系统校准的正确性。

4.4.2 试块的测量实验

对阶梯试块其余厚度部分分别进行连续15次重复性测量，记录回波时间差，并利用标定声速计算测量厚度，结果如表1所示。

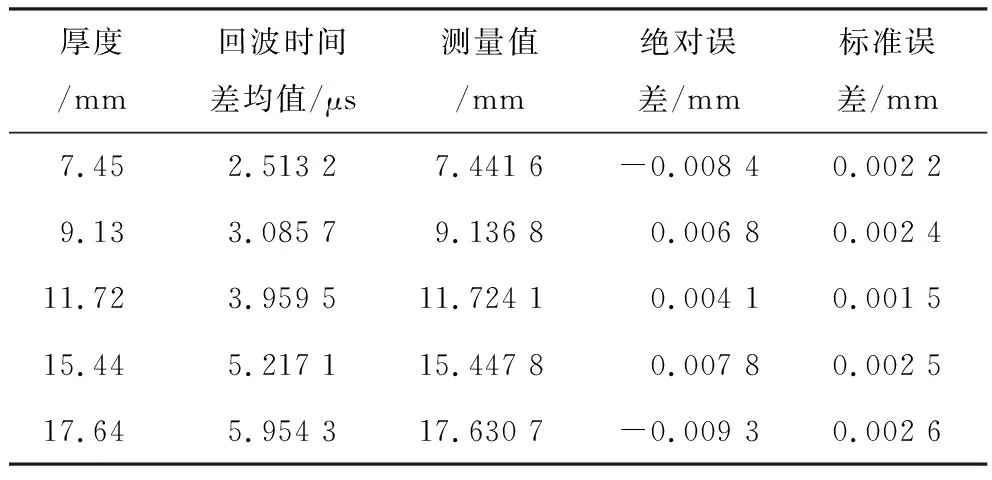
表1 超声测厚结果

对于不同厚度的阶梯试块，系统的测量绝对误差小于0.01 mm，重复性测量标准误差小于0.003 mm。

4.4.3 系统测量时间分析

系统测量时间分配如表2所示。

表2 系统测量时间分配 ms

系统单次测量总时间在15 ms左右，具有较快的测量速度。

5 结束语

根据超声测厚系统的激励与传感信号的特点，设计了一种基于等效时间采样的改进采样方法，弥补了相对低频采样难以适合超声测量的局限。并利用模拟乘法器进行高频超声信号的包络处理，避免了低频采样高频信号信噪比的缺陷。通过FFT粗估信号周期的方法，进行线性移动正弦拟合获取回波相位信息，进一步精确计算回波周期的方法，在15 ms的测量系统响应时间内，使超声测厚精度误差小于0.01 mm，重复稳定性误差小于0.003 mm，为低成本、便携式超声测厚设备的研发提供了一种方案。