面向集群一致性的抗毁性网络分析与设计

陈 浩 王祥科 杨 健

1.国防科技大学智能科学学院 湖南长沙 410073 2.华南理工大学自动化科学与工程学院 广东广州 510640

一致性理论是集群系统分析的最基础的理论之一,在集群分布式估计[1]、分布式优化[2-3]、协同控制[4-6]、协同决策[7-8]等方面有着重要的应用.一致性问题主要是研究如何使网络中的智能体在某些状态或输出达成一致[9-10].在集群一致性问题中,网络的拓扑结构扮演着重要的角色.若网络拓扑为无向图,为实现一致性,通常要求网络为连通图[11-12]；若网络拓扑为有向图,为实现一致性,通常要求网络为有根图[13],即网络中存在某一顶点,使得该顶点到网络中其他任一顶点都存在有向通路,满足这样性质的顶点即为有根图的根.强连通有向图是一类特殊的有根图,此类图中的每一个顶点都是根.

在集群执行任务过程中,不可避免会有通信链路失效或智能体损毁等意外事件发生.其中,通信链路失效,相当于在网络中去掉对应的边,智能体损毁,相当于在网络中去掉对应的顶点.当此两类意外事件发生时,可能会导致达成一致性的拓扑条件不再满足,即无向图不再连通,或有向网络不再是有根图.由于网络拓扑重构的分布式决策过程往往较为复杂,实际在网络拓扑设计时,可考虑增加额外的边,通过冗余设计,使集群具有“抗毁性”,即当去掉网络中一定数量的边或顶点后,无向图依然连通,或有向图依然为有根图.

近年来,在复杂网络领域,网络的抗毁性成为一大研究热点[14],主要借助于图论、统计物理等工具,使用连通度、坚韧度等测度分析抗毁性.在集群协同控制方面,于长斌等基于刚性图的概念,提出了k 边刚性和k 顶点刚性的定义,其含义是网络中去掉k 条边或k 个顶点后,结果仍然是一个刚性图[15]；Jafari 等提出了p 连接能控性和q 智能体能控性的概念,为集群系统在通信链路失效和智能体损毁的情况下的结构能控性提供了度量方法[16].但现有网络抗毁性研究并未从集群一致性的角度分析,如何衡量集群网络在一致性意义下的抗毁性,仍然是一个待解决的问题.

基于此,本文分别针对无向网络和有向网络,从实现集群一致性的拓扑条件出发,提出了抗毁性的概念；对于无向网络,建立了一致性意义下的抗毁性网络与连通度概念的联系；对于有向网络,论文将图论中连通度这一概念进一步拓展,提出了边/顶点连通有根图的概念以刻画有向网络的抗毁性；论文提出了针对一般的有向/无向抗毁性网络的设计方法,并在此基础上,进一步研究了几类特殊的有向抗毁性网络的性质和相应的生成算法.

1 无向抗毁性网络

1.1 无向抗毁性网络的概念

对于无向网络连接的集群系统,为实现一致性,通常要求网络为连通图.但面向复杂环境下集群的运用需求,网络的拓扑设计需要具备一定的冗余度,即满足一定的抗毁性,以保证在局部通信链路失效或部分智能体损毁等意外事件发生后无向网络仍连通.在此给出集群无向抗毁性网络的定义如下.

在此以图1中的例子阐述无向抗毁性网络的定义.图1左图所示的网络结构,当去掉该图中任意一条边,或任意一个顶点及该顶点所连接的边之后,无向网络依然是连通的,因此,该网络结构具有1 边无向抗毁性和1 顶点无向抗毁性；而对于图1右图所示的网络结构,若去掉顶点1 和顶点2 之间的边或顶点2 和顶点3 之间的边,都会造成新得到的网络不再连通；同样,当顶点2 或顶点3 去掉之后,网络也不再连通.因此,图1右图所示的网络不具有抗毁性.

图1 阐释无向抗毁性网络概念的例子Fig.1 Examples to illustrate the concept of undirected survivable networks

对于无向网络,抗毁性的概念与连通度[17]的概念相对应,若网络具有k 边/顶点无向抗毁性,当且仅当具有k+1 边/顶点连通度.现给出一个关于边/顶点连通度的重要定理.

定理1 （Menger 定理[17）]对于无向图,其边/顶点连通度等于中任意两个顶点之间边/顶点不相关的路径数目的最小值.

在定理1 中,两条路径是边不相关的,指这两条路径没有公共的边；两条路径是顶点不相关的,指这两条路径除起始点和终止点之外,没有公共的顶点.由Menger 定理知,若网络具有k 边/顶点无向抗毁性,则中任意两个顶点之间至少有k+1 条边/顶点不相关的路径.显然,两个顶点之间的顶点不相关的路径也是边不相关的,因此,由Menger 定理可以得出如下推论.

1.2 无向抗毁性网络的生成算法

现假设集群网络中所有智能体采用点对点通信的方式,且两两之间的通信代价已知,如何构造k 边/顶点无向抗毁性网络,使网络中总的通信代价最小？

遗憾的是,当k≥2 时,该问题是NP 难.通常,采用贪婪等策略,给出次优解.例如,L.Yang 针对模式识别领域高维流形映射到低维空间的数据嵌入问题,发表了一系列k 边和k 顶点连通无向图的生成算法,包括用于生成k 边连通无向图的k-MST 算法（重复提取k 个最小生成树）[18]、Min-k-ST 算法（寻找总长最小的k 个边不相关的生成树）[19]、k-EC 算法（按边长非减的顺序添加连接两个尚不存在k 条边不相关路径的顶点的边）[20],以及用于生成k 顶点连通无向图的k-VC 算法（按边长非减的顺序添加连接两个尚不存在k 条顶点不相关路径的顶点的边）[21].其中,使用k-MST 算法和Min-k-ST 算法生成的k 边连通无向图边数均为,而使用k-EC 算法生成的k边连通无向图以及k-VC 算法生成的k 顶点连通无向图的边数小于,大于.在此,简要介绍k-EC 算法和k-VC 算法,根据上一节的分析,算法生成的k 边/顶点连通无向图具有k-1 边/顶点无向抗毁性.

k-EC 算法如算法1 所示.该方法将各条边的代价从小到大排序（算法第1 行）,并采用贪婪策略逐一向图中添加各无向边；第4 行至第9 行实质上利用了k 边连通性的传递性：即若顶点和之间有k 条边不相关的无向通路,顶点和之间有k 条边不相关的无向通路,则与之间也存在k 条边不相关的无向通路.算法初始时共设置个组,在运行过程中确保每组中的任意两个顶点之间都有k 条边不相关的无向通路,算法利用k 边连通性的传递性合并各组,直到所有的组最终并入同一组中.两个顶点之间边不相关的无向通路数目检测可以采用网络最大流算法[17].

算法1 k-EC 算法输入：一个无向完全图都有其相应的代价,记作,图中每一条边.输出：一个k 边连通无向图.分到一个单独的组中.1:将初始化：,将每一个顶点中各条边按照代价升序排序2:while do 3: 按序取下一条边4: if v1 和v2 位于不同的组中then 5: if 在图中v1 与v2 边不相关的无向通路小于k then 6:7: else 8: 将v1 与v2 所在的组合并9:10: end if 11: end if 12:end while

k-VC 算法如算法2 所示.值得注意的是,k 顶点连通性并不具备传递性.但k 顶点连通性的一个性质是,若至少有k 个顶点与和之间的顶点不相关的无向通路数均不小于k,则顶点和之间也存在k条顶点不相关的无向通路.k-VC 算法利用这一性质为每一个顶点建立一个集合,当两个集合中有k 个相同元素时,无需再进行顶点不相关无向通路数目的检测.顶点不相关的无向通路数目检测,同样可以采用网络最大流算法.

2 一般的有向抗毁性网络

2.1 有向抗毁性网络的概念

对于有向网络连接的集群系统,为实现一致性,通常要求网络为有根图.在此基础上,为保证集群系统在局部通信中断和部分平台损毁等意外事件下仍能正常工作,需要研究具有抗毁性的有根图网络,使得在去掉有向图中的若干边或顶点之后,依然是有根图.仿照定义1,可给出对有向抗毁性网络的定义如下.

算法2 k-VC 算法输入：一个无向完全图,图中每一条边都有其相应的代价,记作.输出：一个k 顶点连通无向图.初始化：,为每个顶点分配一个集合.中各条边按照代价升序排序2:for 每一条边1:将do 3: if,并且顶点v1 和v2 在中顶点不相关的无向通路数小于k then 4: if v1 和v2 位于不同的组中then 5:6: else 7:8:9: end if 10:end for

本文提出的k 边/顶点连通有根图的定义为图论中的全新概念,目前尚未有关于此类有向图性质的研究.为此,本节简要介绍此类有根图的性质.与无向网络类似,本文在讨论k 顶点连通有根图时假定网络中顶点的数目至少为k+1,以保证在去掉网络中的k-1个顶点后,网络中至少仍有2 个顶点,从而能够继续分析网络中剩余个体的一致性.

对于无向网络而言,k 顶点连通是一个比k 边连通更严格的条件,即若网络具有k 顶点无向抗毁性,则其必然具备k 边无向抗毁性,反之则不然.对于有向网络而言,类比无向网络,显然并非所有的k 边连通有根图都是k 顶点连通有根图；但同时,也并非所有的k 顶点连通有根图都是k 边连通有根图.

现讨论k 边/顶点连通有根图中,k 与各顶点入度及出度的关系.记为顶点v 的入度,为顶点v 的出度,,

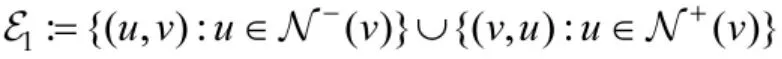
采用同样的思路可证明式（2）与式（3）成立.证毕.

现讨论无向抗毁性与有向抗毁性的关系.当一无向图的每一条边替换为方向相反的两条有向边后,可以得到一有向图.而把一k 边连通无向图的各边都替换为方向相反的两条边后,得到的有向图是2k 边连通有根图.为证明这一点,首先给出如下引理.

由此可得出如下定理.

定理2 所对应的k 顶点版本如下.

定理3 可以很容易证明.现以图2的例子对定理2 和定理3 加以说明.图2左侧的无向图为2 顶点连通无向图,当其所有的边替换为方向相反的有向边后,得到的图只是2 顶点连通有根图,若去掉该图的任意两个不相邻的顶点及与之连接的边后,将只剩两个孤立的顶点.根据命题1,图2左侧的无向图也是2边连通无向图,当其各边替换为有向边时,可以验证,去掉任意3 条边后仍为有根图,即图2右侧的图为4边连通有根图.

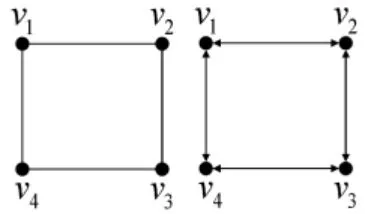
图2 2 顶点连通无向图及替换后的有向图Fig.2 2-vertex-connected undirected graph and the corresponding digraph after replacing its edges

2.2 有向抗毁性网络的生成算法

定理2 和定理3 建立了集群一致性意义下有向抗毁性网络与无向抗毁性网络之间的关系,根据这两个定理的分析,可以利用无向抗毁性网络的生成算法得到有向抗毁性网络.

对于k 边连通有根图,本文提出了k-ECRU 算法（k-Edge connected rooted digraphs from undirected graphs）,如算法3 所示.该算法首先使用k-EC 算法生成无向图,若k 是偶数,则生成k/2 边连通无向图；若k 是奇数,则生成（k+1）/2 边连通无向图；然后将该无向图的每一条边替换为方向相反的两条有向边；注意当k 为奇数时,上述步骤得到的实质上是k+1边连通有根图,因而此时再去掉一条代价最大的边.采用上述算法即可得到k 边连通有根图,该图具有k+1 边有向抗毁性.

与k 边连通有根图的生成算法类似,对于k 顶点连通有根图,本文提出了k-VCRU 算法（k-Vertex connected rooted digraphs from undirected graphs）,如算法4 所示.该算法利用k-VC 算法生成k 顶点连通无向图,再将该图的每一条无向边替换为方向相反的两条有向边,即得到k 顶点连通有根图,该图具有k+1顶点有向抗毁性.另外,由于k-VC 算法生成的无向图也是k 边连通无向图,因此,根据定理3,k-VCRU算法生成的有向图也是2k 边连通有根图,具有2k-1边有向抗毁性.

算法3 k-ECRU 算法输入：包含n 个顶点的有向完全图,图中每一条边都有其相应的代价,记作.输出：一个k 边连通有根图.初始化：.1: 将转化为无向完全图,对中的每一条边,设置其代价为2:if k 是偶数then 3: 使用k-EC 算法生成k/2 边连通无向图4: 将每一条无向边替换为两条有向边和,得到5:else 6: 使用k-EC 算法生成（k+1）/2 边连通无向图7: 将每一条无向边替换为两条有向边和,得到8: 去掉一条中代价最大的边,得到.9:end if

算法4 k-VCRU 算法输入：包含n 个顶点的有向完全图,图中每一条边都有其相应的代价,记作.输出：一个k 边连通有根图.初始化：.1: 将转化为无向完全图,对中的每一条边,设置其代价为2:使用k-VC 算法生成k 顶点连通无向图3: 将每一条无向边替换为两条有向边和,得到

3 几类特殊的有向抗毁性网络

第2 章针对集群一致性意义下有向网络的抗毁性,提出了k 边/顶点连通有根图的概念,并设计了用于生成一般的k 边连通有根图的k-ECRU 算法和生成一般的k 顶点连通有根图的k-VCRU 算法.本章在此基础上,讨论k=2 和k=3 这两种特殊的情形.

3.1 2 边/顶点连通有根图

对于k 边/顶点连通有根图,当k=1 时,则退化为一般的有根图.现讨论k=2 的情形.

由命题2 可以看出,在k 边连通有根图中,对根顶点和非根顶点的入度有不同的要求.若,则有向图的每个顶点都是根顶点,相应地,有向图为强连通图.对于强连通图,有如下结论.

命题3 强连通图都是2 边连通有根图.

反之并不成立,即2 边连通有根图并不一定是强连通图.

另一方面,并非所有的强连通图都是2 顶点连通有根图.命题4 给出了一个比强连通更严苛的条件,以保证有根图是2 顶点连通有根图.

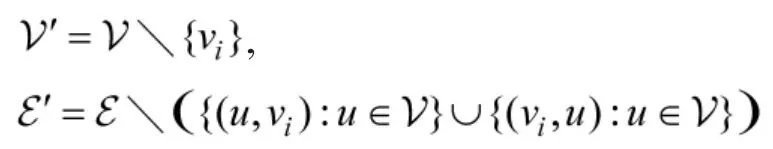
现在分析边数最少的2 边/顶点连通有根图的形式.有如下定理成立.

根据定理4,边数最少且通信代价最小的2 边/顶点连通有根图问题,等价于求解最小Hamilton 回路的旅行商问题.

3.2 3 边/顶点连通有根图

定理4 分析了k=2 时,k 边/顶点连通有根图所包含的最少边数.现分析k=3 的情形.首先考虑3 边连通有根图.显然,只包含2 个顶点的简单有向图至多只有2 条边,故在讨论3 边连通有根图时,限定

1）若顶点v*的入度为0,则图中其他顶点均为非根顶点,根据命题2（a）,这些顶点的入度均不小于3.因此,该情形下.此外,为确保简单有向图为3 边连通有根图,需保证.

2）若顶点v*的入度为1,由于其他顶点的入度至少为2.因此,.

算法5 3 边连通有根图构造算法输入：顶点集.输出：一个3 边连通有根图.1:生成一个Hamilton 回路,得到图2: 向图中添加所有与中的边方向相反的边,得到图3:去掉中任意一条边,新的边集记为,得到

现讨论3 顶点连通有根图所包含的最少边数.

1）有3 个顶点的入度恰好为1,并且这3 个顶点构成一条有向回路.在图中,不能再有由其他顶点指向这3 个顶点的边,否则这3 个顶点的入度会大于1,不满足该条件.因而只有这3 个顶点为有根图的根顶点.此外,除这3 个顶点外,其余顶点的入度至少为3.为证明这一点,记这3 个根顶点分别为,和,则必存在一顶点以及由某个根顶点指向顶点的边.不失一般性,记这条边为（,）,若顶点的入度仅为2,记指向顶点的另外一条边为.当去掉顶点和及与之相连的边后,得到的有向图中,仍然有原有向图的根顶点和,但并无有向边指顶点,因此,不是有根图,这与是3 顶点连通有根图矛盾.因此,顶点的入度至少为3；同样地,存在顶点v5以及由顶点-中的某个顶点指向顶点v5的边,采用同样的方法可以证明顶点v5的入度至少为3；以此类推,可以证明除3 个根顶点外,其余顶点的入度至少为3.因此,该情形下,.

2）恰好有2 个顶点的入度小于2,现证明当其余顶点的入度均为2 时,这两个顶点的入度均为1.若不然,不妨设顶点的入度为0,顶点的入度为1.根据上述分析,；并且除顶点和之外,其余顶点的入度均为2.为保证去掉顶点或或二者同时去掉后,得到的有向图仍然是有根图,则必须有一个顶点是有向图的根顶点,并且.由于是图'的根顶点,因而存在顶点满足.由于,则要么,要么.若,则图去掉顶点和后,得到的有向图将不再是有根图,与是3 顶点连通有根图矛盾.同理,同样会与是3 顶点连通有根图的前提矛盾.因此,该情形下.

算法6 3 顶点连通有根图构造算法输入：n 个顶点组成的集合.输出：一个3 顶点连通有根图.1:生成一个Hamilton 回路,得到图2:沿Hamilton 回路,将各顶点依次标记为,新的边集记为3:向中逐次添加边,得到

4 仿真分析

通过一个典型算例,进一步阐释本文提出的面向集群一致性的网络抗毁性概念,以及抗毁性网络的设计算法.

如图3（a）所示,100 个智能体随机分布在1 000×1 000 的区域内,用智能体两两之间的距离表示通信代价,现针对这些智能体设计有向抗毁性网络.

分别采用k-ECRU 算法和k-VCRU 算法设计2边连通有根图和2 顶点连通有根图.对于2 边连通有根图,k-ECRU 算法首先使用k-EC 算法生成一个1边连通无向图,此时,相当于使用Kruskal 算法生成一个最小生成树,如图3（b）所示.将这个无向图的每一条边替换为方向相反的两条有向边,即得到k-ECRU 算法生成的2 边连通有根图,该图具有1 边有向抗毁性,但不具备1 顶点有向抗毁性.对于2 顶点连通有根图,k-VCRU 算法首先使用k-VC 算法生成一个2 顶点连通无向图,如图3（c）所示.该无向图具有1 顶点无向抗毁性,将其每一条边替换为方向相反的两条有向边后,即得到k-VCRU 算法生成的2 顶点连通有根图,该图既有1 顶点有向抗毁性,也具有3 边有向抗毁性.图3（d）为使用蚁群算法得到的最优Hamilton 回路,将回路指定方向后对应的有向图也是最优的2 边/顶点连通有根图.

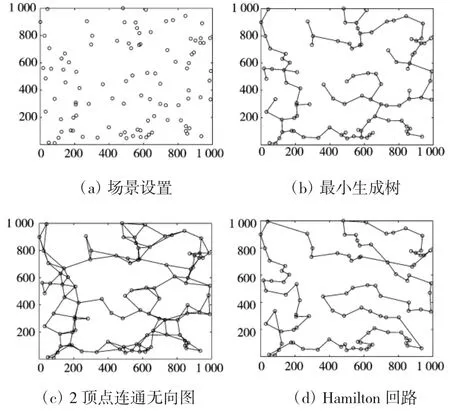
图3 场景设置及相应算法生成的无向图Fig.3 Simulation settings and the undirected graphs obtained with the corresponding algorithms

表1比较了几种算法得到的2 边/顶点连通有根图.从中可以看出,3.1 节提出的采用Hamilton回路生成2 边/顶点连通有根图的算法,不仅能得到具有1边和1 顶点有向抗毁性的网络,也使得网络中边的数目和总的通信代价显著降低.

表1 几种算法得到的2 边/顶点连通有根图比较Table 1 Comparison of the 2-edge-connected and 2-vertexconnected rooted digraphs obtained with different algorithms

进一步考虑3 边/顶点连通有根图.分别执行算法3～算法6,其中,执行算法5 时用到的Hamilton 回路即采用图3（d）中的Hamilton 回路,算法第3 行去掉的边选择代价最大的边.执行算法6 时同样选择图3（d）中的Hamilton 回路,第2 行标记顶点时选择能够使得总代价最小的方式.几种算法最终得到的3 边/顶点连通有根图的情况如表2所示.从表中可以看出,除k-VCRU 算法外,其余算法均无法同时保证2边抗毁和2 顶点抗毁,但采用k-VCRU 算法生成的有向图边数和总代价都明显高于其余三者；而3.2 节专门针对3 边/顶点连通有根图设计的算法5 和算法6 能够在确保2 边抗毁或2 顶点抗毁的前提下,显著降低边数和总代价.

表2 几种算法得到的3 边/顶点连通有根图比较Table 2 Comparison of the 3-edge-connected and 3-vertexconnected rooted digraphs obtained with different algorithms

5 结论

随着集群系统的不断发展及其在作战领域应用的不断成熟,如何提升集群系统在复杂条件下的容错性,更好地发挥集群的优势,成为集群指挥控制领域的一个重要课题.本文面向一致性这一集群协同的基础问题,提出了面向集群一致性的抗毁性网络概念,并从图论的角度,分析了此类网络的性质,并设计了抗毁性网络的生成算法,提升了集群网络的容错性.

本文提出的面向集群一致性的抗毁性网络是图论中的全新概念,本研究还处于起步阶段.特别是针对具有有向抗毁性的k 边/顶点连通有根图,分析推导此类网络图结构的更多性质,并对k 为一般正整数时,设计更为优化的网络生成算法将是下一步研究的重点.此外,在集群leader-follower 协同跟踪等问题中,如何与leader 选择方法结合,确保在部分智能体损毁时具备leader-follower 一致性,同样是一个值得研究的问题.