碱激发矿渣/粉煤灰净浆/砂浆力学性能研究
2022-11-01庄培镇马玉玮罗甜恬刘卫森傅继阳
庄培镇,马玉玮,罗甜恬,刘卫森,傅继阳
(广州大学风工程与工程振动研究中心,广州 510006)
0 引 言
碱激发材料又称“地质聚合物”[1],是以活性硅铝酸盐(如矿渣、粉煤灰、偏高岭土等)为原材料,在碱性条件下生成的具有胶凝性能的材料,现已成为最具发展潜力的绿色低碳胶凝材料之一。与水泥相比,碱激发材料拥有快凝早强、水化热低、耐化学腐蚀[2]、耐高温、抗冻融[3]等优点。关于碱激发材料的工程应用研究,主要包括碱激发混凝土梁、板、柱及砌块[4]等方面。近年来,已有大量关于碱激发材料力学性能的研究,主要包括抗压强度、弹性模量、泊松比、单轴压缩应力-应变关系等方面。抗压强度是碱激发材料主要的静态力学性能之一,主要受原材料种类、碱激发剂种类和用量、水灰比、养护条件等因素的影响。Davidovits[5]制备了偏高岭土基碱激发砂浆,在20 ℃养护4 h后,其抗压强度可以达到20 MPa,且28 d抗压强度可达70~100 MPa。郭晓潞等[6]使用水玻璃作为激发剂,激发高钙粉煤灰和热活化污泥制备碱激发材料,在75 ℃高温下养护24 h的抗压强度达70 MPa,室温(23 ℃)下养护28 d的抗压强度达52 MPa。Nazari等[7]利用稻壳灰取代30%(质量分数)粉煤灰制备碱激发胶凝材料,在80 ℃下养护28 d后,其抗压强度达58.9 MPa。Zhang等[8]以粉煤灰和赤泥作为原材料,制备的碱激发胶凝材料在常温养护条件下28 d抗压强度最高可达21.3 MPa。以上研究表明,对活性硅铝酸盐原材料使用不同的激发剂激发,在适当的养护条件下可以提高材料的抗压强度,增强力学性能。
材料的弹性模量是研究材料特性的重要参数。混凝土的弹性模量取决于粗骨料的类型和含量以及砂浆的弹性模量,砂浆的弹性模量取决于细骨料的类型和含量以及净浆的弹性模量。目前,关于碱激发材料的弹性模量结果存在一定的争议。Collins等[9]发现,使用不同激发剂的碱激发矿渣混凝土的弹性模量略低于普通硅酸盐混凝土。Douglas等[10]提出,碱激发矿渣混凝土的弹性模量可以通过美国混凝土结构建筑规范(ACI318—08)中相应的抗压强度来估算。并且,Yang等[11]研究表明,利用氢氧化钙作为激发剂生成的碱激发矿渣混凝土的弹性模量可以由美国混凝土结构建筑规范(ACI318—08)近似预测。Fernndez-Jiménez等[12]研究结果显示,碱激发粉煤灰混凝土的弹性模量在10~20 GPa范围内,而普通硅酸盐水泥混凝土的弹性模量在25~35 GPa,弹性模量更高。而Joseph等[13]通过试验发现,碱激发粉煤灰混凝土经过60~120 ℃养护之后的弹性模量在40~60 GPa,远高于同等抗压强度的普通硅酸盐混凝土。对于应力-应变曲线的研究,碱激发材料主要集中在混凝土方面,但研究相对较少。混凝土材料的应力-应变关系是混凝土结构非线性分析中最基本的本构关系,研究者往往利用水泥混凝土应力-应变关系的经验公式来预测碱激发材料的变化规律。Yang等[11]、Thomas等[14]研究的应力-应变关系结果显示,初始刚度和峰值应力时的应变随着抗压强度的增加而增加,与普通硅酸盐水泥规律一致。
目前针对碱激发材料的研究主要集中在反应机理及反应产物等方面,由于原材料、试验环境的差异性,碱激发材料的力学性能差异较大,暂无统一定论,特别是针对不同组成的碱激发材料的弹性模量,应力-应变曲线的研究相对较少。鉴于此,本文研究了不同矿渣掺量、细骨料掺量对碱激发矿渣/粉煤灰净浆/砂浆力学性能的影响规律,主要测试了抗压强度、弹性模量、应力-应变曲线等,得到了碱激发矿渣/粉煤灰净浆/砂浆的无量纲曲线,参考不同本构模型进行比较分析。本文对建立碱激发材料相关工程规范,推进碱激发材料的工程应用做出一定贡献。
1 实 验
1.1 材 料
试验采用S95级矿渣和F类粉煤灰,分别来源于韶关钢铁厂和广东省中山发电厂,其化学成分如表1所示,粒度分布如图1所示。碱激发剂为工业级水玻璃,通过化学滴定法测定其SiO2和Na2O的质量分数,分别为28.18%和12.19%。采用NaOH(分析纯)调节水玻璃模数,改变碱激发剂中Na2O的含量。细骨料为某砂厂河砂,筛分试验结果如表2所示。经计算,细度模数Mx=2.76,符合中砂级配要求,物理性能如表3所示。试验用水为去离子水。

表1 粉煤灰与矿渣的化学组成Table 1 Chemical composition of fly ash and slag

图1 原材料的粒径分布Fig.1 Particle size distribution of raw materials

表2 砂的筛分试验结果Table 2 Screening test results of sand

表3 砂的物理性能Table 3 Physical properties of sand
1.2 试验方法
本试验设计包括不同矿渣掺量净浆/砂浆及不同细骨料掺量的砂浆碱激发材料,所有配比激发剂模数为1.5,Na2O和SiO2的质量分数分别为4%和6%,净浆水胶比(W/B)为0.40,砂浆水胶比为0.42,具体配比如表4所示。按照试验设计对试块进行分组,每组制样6个,先将水、氢氧化钠、水玻璃按表4配制成对应含量的激发剂,并将其静置1 d。根据原材料配比进行称料,均匀混合搅拌后,在搅拌锅中混合加入激发剂,在水泥净浆/砂浆搅拌机中搅拌4 min,其中慢搅2 min,快搅2 min。然后将浆体注入40 mm×40 mm×40 mm和40 mm×40 mm×160 mm的试模内振动成型,在20 ℃、相对湿度95%的标准养护条件下养护1 d,然后脱模进行标准养护,测定龄期分别为7 d和28 d,测定样品的抗压强度、弹性模量及应力-应变曲线。抗压强度测试依照《水泥胶砂强度检验方法(ISO法)》(GB/T 17671—1999)[15],弹性模量测试依照《混凝土物理力学性能试验方法标准》(GB/T 50081—2019)[16]。

表4 碱激发矿渣/粉煤灰净浆/砂浆的试验配比Table 4 Test mix proportion of alkali-activated slag/fly ash paste/mortar
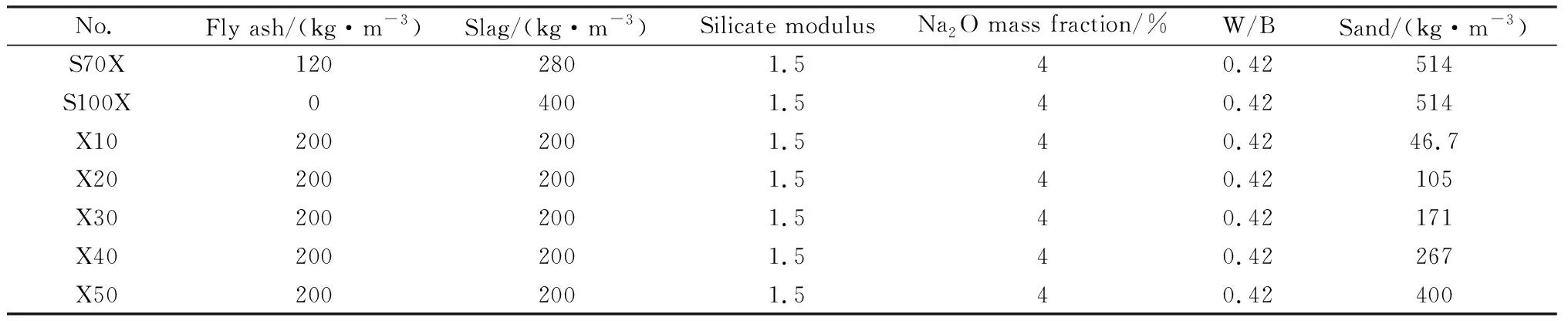
续表
2 结果与讨论
2.1 矿渣/细骨料掺量对抗压强度的影响
图2显示了不同矿渣掺量的碱激发矿渣/粉煤灰净浆/砂浆抗压强度。从图中可知,碱激发净浆/砂浆的抗压强度均随矿渣掺量的增加而增大,且碱激发净浆强度均高于砂浆强度。当矿渣掺量从50%(质量分数,下同)增加至70%时,净浆7 d抗压强度增长51.42%,砂浆7 d抗压强度增长30.98%,28 d抗压强度分别增长21.14%与39.43%,增幅明显;而当矿渣掺量从70%增加到100%时,抗压强度增幅不大。试验结果与Puertas等[17]对碱激发矿渣/粉煤灰净浆的研究结果一致。Fang等[18]也研究了矿渣掺量对碱激发矿渣/粉煤灰混凝土的影响规律,证明了矿渣的掺入能够显著提高抗压强度,对早期强度的影响尤其明显。粉煤灰与碱激发剂发生反应,形成非晶态沸石类的碱性硅铝酸盐凝胶[19],然而粉煤灰的活性较低,需要在碱性条件下溶出尽可能多的Al和Si,重新聚合生成N-A-S-H凝胶,才能使浆体具有一定的强度。随着矿渣含量逐渐增加,矿渣氧化物中的CaO和MgO含量较高,在碱性环境下,矿渣玻璃体发生分散、溶解,水化产物主要为低钙硅比的C-(A)-S-H凝胶。C-(A)-S-H凝胶结构无序程度和孔隙率低,是材料产生强度的主要物质[20]。从而浆体的结构更加致密,抗压强度随之提高。碱激发砂浆7 d/28 d抗压强度相对净浆均有不同程度的降低,说明细骨料的掺入可能会使试样产生更多的孔隙,试样承受荷载时孔隙的大小和分布会影响裂纹的产生,从而影响试样的抗压强度。

图2 矿渣掺量与碱激发材料抗压强度的关系Fig.2 Relationship between slag content and compressive strength of alkali-activated materials
图3显示了不同细骨料掺量的碱激发矿渣/粉煤灰砂浆的抗压强度。从图中分析得出,抗压强度随着细骨料掺量增多而减小,当细骨料掺量增加至40%(质量分数,下同)时,会出现明显的“抗压强度下降点”。Joseph等[13]研究了骨料对碱激发混凝土力学性能的影响,研究表明,骨料与浆体之间的界面过渡区是最薄弱的结构,承受强度的能力主要由界面过渡区决定。有研究[21]表明,碱激发砂浆中也存在“界面过渡区决定整体强度”的准则,且取决于骨料的掺量,本试验结果与该研究观点一致。Fang等[22]从纳米尺度和微观尺度研究了碱激发矿渣-粉煤灰混凝土界面过渡区的微观力学性能,结果表明,碱激发矿渣-粉煤灰在砂浆界面过渡区微观力学性能良好,相较于水泥砂浆的界面过渡区具有更高的弹性模量。
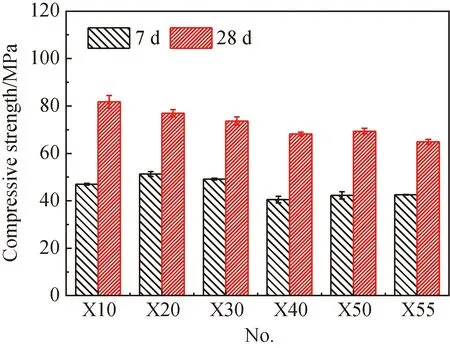
图3 细骨料掺量与碱激发砂浆抗压强度的关系Fig.3 Relationship between fine aggregate content and compressive strength of alkali-activated mortar
2.2 矿渣/细骨料掺量对弹性模量的影响
图4显示了矿渣掺量对碱激发矿渣/粉煤灰净浆/砂浆不同龄期弹性模量的影响规律。由图可知:矿渣掺量从50%增加至70%时,净浆/砂浆7 d和28 d弹性模量增幅明显;矿渣掺量增至100%时,净浆/砂浆7 d弹性模量出现下降,28 d弹性模量增幅不大,与掺量70%时数值接近。碱激发砂浆7 d和28 d弹性模量相对净浆更高,可见,细骨料的掺入使材料弹性模量增大,提高碱激发材料抵抗变形的能力,使其韧性变好。细骨料的掺入对7 d早期力学性能的影响更为明显,弹性模量提高率为70%~90%,而28 d提高率较小,可能是由于早期水化程度还未完全,受细骨料掺入影响明显,相较龄期为7 d时,碱激发材料砂浆28 d时水化程度更高,体系趋于稳定。在试验过程中,也可以明显感受到净浆属于“爆裂”型破坏,而砂浆为“沉静”型破坏。本研究所得碱激发净浆28 d弹性模量在12.83~19.53 GPa,砂浆28 d弹性模量在18.72~23.10 GPa。Fernndez-Jiménez等[23]使用低钙粉煤灰制成的碱激发粉煤灰混凝土弹性模量在17~18 GPa,Thomas等[14]使用高钙粉煤灰制成的碱激发粉煤灰混凝土弹性模量在28~47 GPa,研究表明,原材料为低钙粉煤灰制成的碱激发材料的弹性模量普遍低于原材料为高钙粉煤灰制成的碱激发材料。本研究为低钙粉煤灰制得的碱激发体系,与其他学者研究规律一致。
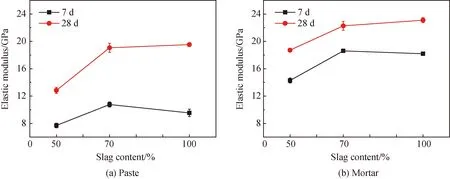
图4 矿渣掺量与碱激发材料弹性模量的关系Fig.4 Relationships between slag content and elastic modulus of alkali-activated materials
图5显示了细骨料掺量对碱激发矿渣/粉煤灰砂浆弹性模量的影响规律。从图中可以看出, 碱激发砂浆的7 d弹性模量随着细骨料掺量增加而整体呈增大趋势,7 d弹性模量变化范围为7.68~14.28 GPa,28 d弹性模量为13.18~18.72 GPa。从图中弹性模量的变化区间可以看出:当细骨料掺量为10%~30%时,7 d弹性模量为7.68~9.09 GPa,28 d弹性模量为13.18~14.58 GPa;当细骨料掺量为40%~55%时,7 d弹性模量为9.02~14.28 GPa,28 d弹性模量为18.28~18.72 GPa。当细骨料掺量为40%时,弹性模量出现明显增大。结合前面抗压强度试验结果可知:当细骨料掺量为10%~30%时,碱激发砂浆承受轴心压力时的荷载主要由浆体部分承担,界面过渡区影响较小;当细骨料掺量为30%~40%时,界面过渡区影响增大;当细骨料掺量为40%~55%时,碱激发砂浆承受轴心压力时的荷载由浆体、界面相、骨料共同承担。因此,弹性模量的变化规律进一步说明,当细骨料掺量为30%~40%时,细骨料在碱激发材料承载受力过程中起到较为明显的作用,从而影响弹性模量数值,与抗压强度的规律相一致。
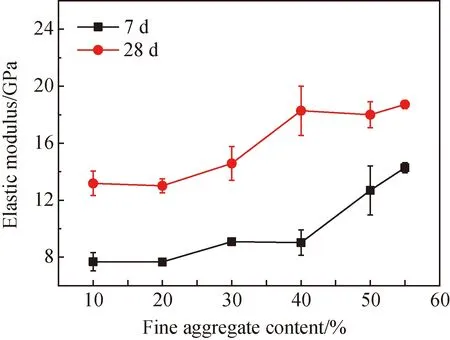
图5 细骨料掺量与碱激发砂浆弹性模量的关系Fig.5 Relationship between fine aggregate content and elastic modulus of alkali-activated mortar
2.3 碱激发矿渣/粉煤灰应力-应变曲线拟合与修正
应力-应变曲线所呈现的宏观变化过程是研究混凝土结构和构件承载和变形的主要分析手段和依据。应力-应变曲线包括上升段和下降段两个部分,是混凝土在不同受力阶段的变形,如内部裂缝的产生和发展、达到强度极值、峰值后的残余应力状态、试样表面的破碎和完全破坏等一系列变化过程的宏观反应。关于碱激发净浆/砂浆的受压应力-应变关系目前还没有统一的本构模型,本研究尝试参考经典的混凝土本构模型,令x=ε/ε0,y=σ/σ0, 其中σ、ε分别为应力、应变,σ0、ε0分别为曲线的峰值应力、峰值应变。现有的应力-应变曲线方程表达式如表5所示。

表5 现有应力-应变曲线方程表达式[24]Table 5 Existing stress-strain curves equation[24]
2.3.1 受压应力-应变上升段曲线方程
通过前人大量的实践[25-26]发现,采用多项式的形式能够较好地反映普通硅酸盐水泥混凝土的受压应力-应变过程,对试验数据进行无量纲化处理,以碱激发净浆/砂浆压应变ε与其峰值压应变ε0之比为横坐标,以碱激发净浆/砂浆压应力σ与其峰值压应力σ0之比为纵坐标,碱激发矿渣/粉煤灰净浆/砂浆上升段受压应力-应变关系曲线如图6所示。
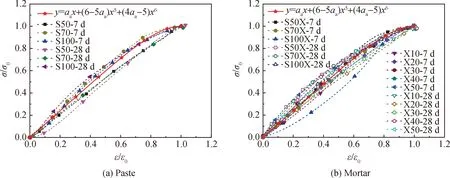
图6 碱激发净浆/砂浆受压应力-应变上升段拟合曲线Fig.6 Fitting curves of compressive stress-strain rising section of alkali-activated paste/mortar
从已提出的混凝土受压应力-应变曲线表达式可知,分段式的方程符合应力-应变曲线的大部分几何特点,能够较为完整、准确地拟合试验曲线,反映混凝土的全部受力性能。过镇海等[25]建议采用两段式应力-应变关系方程,该方程对普通混凝土的拟合效果很好。此外,吴有明[24]、谭彬[26]也提出采用分段式的公式来拟合应力-应变曲线。本文分别采用过镇海等[25]提出的拟合公式(见式(1))和吴有明[24]提出的拟合公式(见式(2))来进行受压上升段的拟合,拟合结果如表6所示。

表6 不同拟合公式拟合结果Table 6 Fitting results of different fitting formulas
过镇海-修正单轴受压应力-应变关系方程:
(1)
吴有明-修正单轴受压应力-应变关系方程:
(2)
式(1)中E0为混凝土的初始切线弹性模量,GPa。公式中上升段参数aa表示混凝土原点切线模量和峰值割线模量的比值,下降段参数ad表示下降段曲线的陡峭程度,反映了混凝土的塑性。两个参数能够反映混凝土的一些重要特征,如变形模量(曲线斜率)的变化情况,延性和吸收能量(曲线与x轴所围面积)的多少,因而能够作为数量指标来比较或者衡量不同强度等级混凝土的受力性能差异。如aa越小、ad越大,则曲线越陡,与x轴所围面积越小,表明此材料塑性变形小,破坏过程较快,材质较脆;反之,则材料变形较大,破坏缓慢,存在良好延性。
由表6可知拟合效果良好,过镇海拟合公式得出的aa规律不明显,而吴有明拟合公式得出的aa呈规律性变化,大多落在0.9≤aa≤1.4范围内,试验曲线与理论曲线比较接近。根据应力-应变关系试验结果及拟合公式的拟合效果,本文建议采用吴有明的分段式方程对碱激发材料受压应力-应变关系进行描述,表达式为
(3)
由于试验测试无法测得应力-应变曲线的下降段,此处仅假定碱激发材料的应力-应变曲线下降段符合公式(3)。Rangan等[27]研究了碱激发粉煤灰混凝土在单轴压缩作用下的应力-应变曲线关系,证明了试验测得的应力-应变关系与Collins等[28]建立的高强混凝土模型近似,碱激发材料的应力-应变全曲线是否可以借鉴普通混凝土的模型进行修正,还有待进一步研究。
2.3.2 受压应力-应变全曲线修正及结果讨论
碱激发矿渣/粉煤灰净浆/砂浆单轴受压的应力-应变曲线试验结果如表7所示,应力-应变曲线及其修正曲线(实线)如图7~图12所示。修正曲线上升段与实测曲线基本重合,这反映了实验值与模拟值高度吻合。
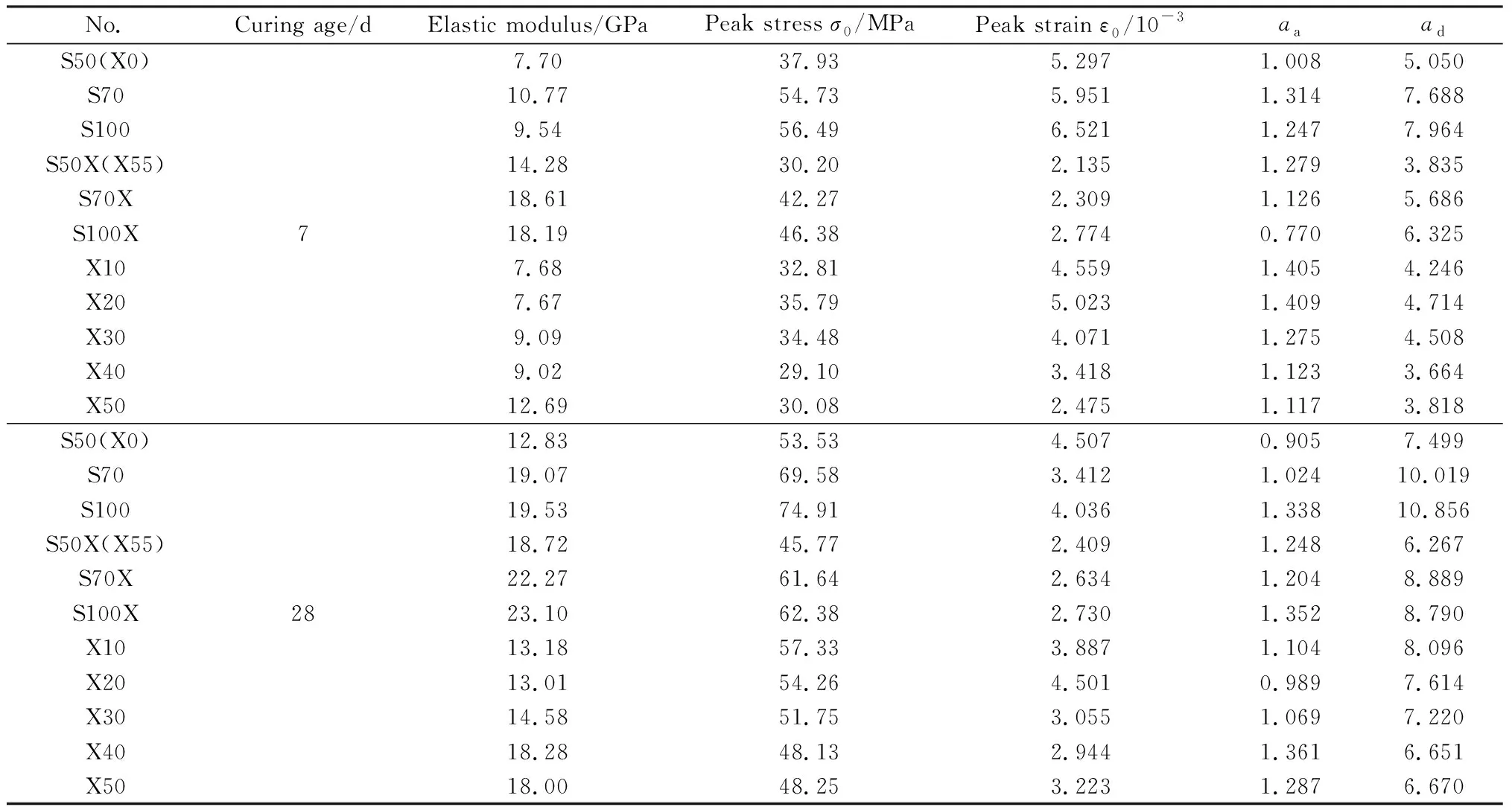
表7 净浆/砂浆静力试验结果及修正系数计算表Table 7 Static test results and correction coefficient calculation table of paste/mortar
图7、图8显示了矿渣掺量对碱激发矿渣/粉煤灰净浆不同龄期应力-应变曲线的影响规律。根据应力-应变上升段曲线可知,随着矿渣掺量增加,曲线上升段的斜率增大,表明净浆的弹性模量升高。与此同时净浆的峰值应力逐渐增大,当矿渣掺量从50%增加至70%时,净浆7 d峰值应力增长44.29%,28 d峰值应力增长29.98%,而当矿渣掺量从70%增加到100%时,7 d和28 d峰值应力增长幅度不大。表明一定量矿渣的掺入对于早期强度的提高较为明显。结合表7可知,当矿渣掺量由70%增至100%时,净浆7 d峰值应变提升了9.58%,28 d峰值应变增加了18.29%。这是由于单位体积内混凝土凝胶含量越多,其峰值应变越大[29]。当矿渣掺量增加时,体系水化反应程度更高,水化产物含量增多。对于龄期而言,相同矿渣掺量下净浆对应的峰值应变随着龄期的增长反而出现下降。由于养护时间的增长,试样内部收缩产生裂纹[30],受压时裂纹扩展,其峰值应变出现下降。峰值应力后,应力-应变曲线进入下降段,随着矿渣掺量的增加,下降段逐渐变陡,说明净浆的脆性更加显著。
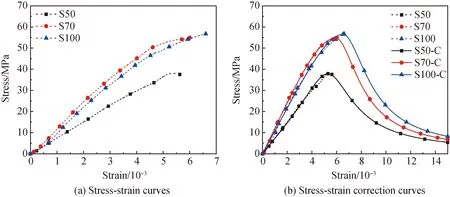
图7 龄期7 d时不同矿渣掺量净浆的应力-应变曲线Fig.7 Stress-strain curves of paste with different slag content in 7 d

图8 龄期28 d时不同矿渣掺量净浆的应力-应变曲线Fig.8 Stress-strain curves of paste with different slag content in 28 d
图9、图10显示了矿渣掺量对碱激发矿渣/粉煤灰砂浆不同龄期应力-应变曲线的影响规律。由图9(a)可以看到100%矿渣掺量的砂浆上升段初始阶段较为平缓,有一个明显的应力增长台阶,这可能是材料内部被压实的过程。根据应力-应变上升段曲线可知,7 d龄期时,随着矿渣掺量的增加,峰值应力增大,强度增强较为明显,表明矿渣的掺入有利于提高碱激发砂浆的早期强度。随着矿渣掺量的增加,试样的峰值应变有所增长,但幅度不大,说明矿渣掺量对碱激发砂浆的峰值应变影响不大。在应力-应变下降段,随着矿渣掺量增加,下降段变陡(参数ad变大),说明材料破坏过程较快,材质较脆,与净浆规律一致。

图9 龄期7 d时不同矿渣掺量砂浆的应力-应变曲线Fig.9 Stress-strain curves of mortar with different slag content in 7 d
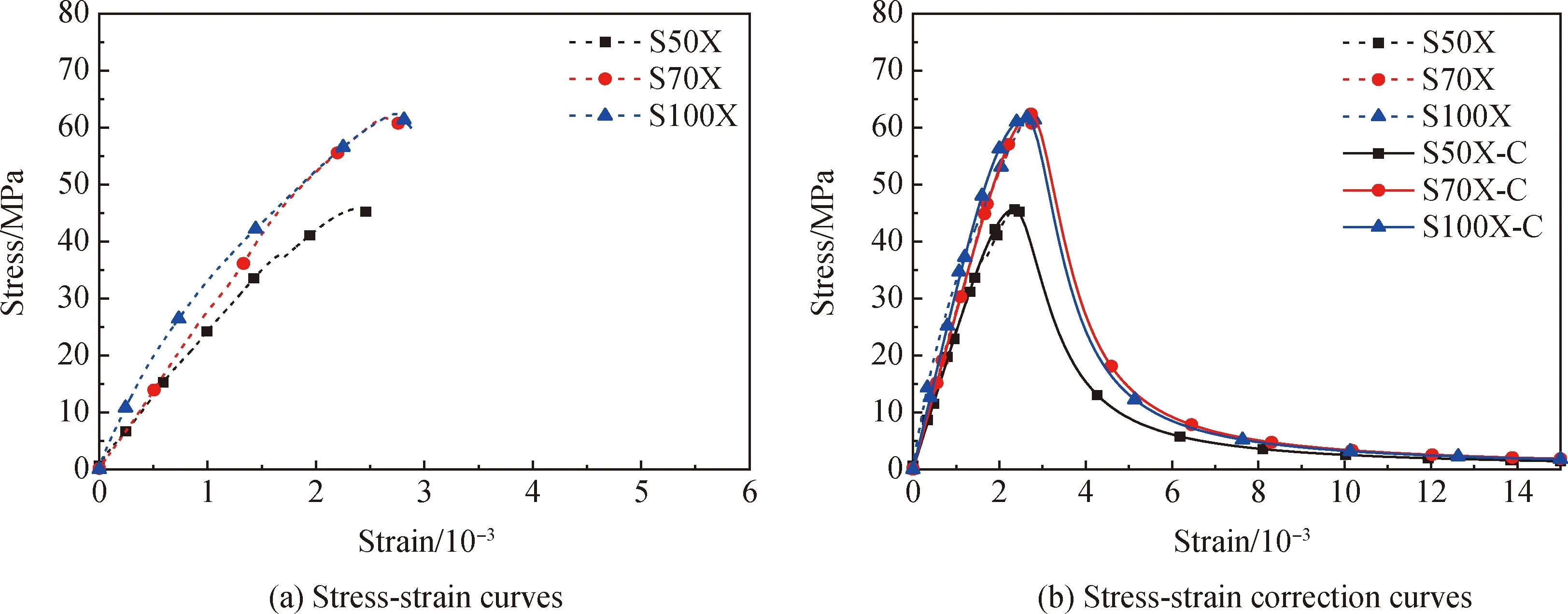
图10 龄期28 d时不同矿渣掺量砂浆的应力-应变曲线Fig.10 Stress-strain curves of mortar with different slag content in 28 d
结合图7~图10,并且根据表7中应力-应变曲线拟合结果可以看出,随着细骨料的掺入,碱激发砂浆7 d和28 d受压时弹性模量增大,峰值应力和峰值应变相对降低,下降段曲线变缓,破坏时延性较好。例如矿渣掺量为50%的净浆(X0)掺入细骨料(X55)时,7 d和28 d的应力-应变上升段曲线斜率增大,对应的7 d弹性模量从7.70 GPa增加到14.28 GPa,28 d弹性模量从12.83 GPa增加到18.72 GPa。而峰值应力和峰值应变相对降低,7 d和28 d的峰值应力分别下降了20.38%和14.50%,峰值应变分别下降了59.69%和46.55%。7 d和28 d的下降段曲线变缓,参数ad分别降低了24.06%和16.43%,说明碱激发砂浆破坏过程较慢,延性较好。
图11、图12显示了细骨料掺量对碱激发矿渣/粉煤灰砂浆应力-应变曲线的影响规律。可以看出,随着细骨料掺量从10%增加到30%,碱激发砂浆7 d应力-应变上升段曲线斜率增大,砂浆弹性模量从7.68 GPa增加到9.09 GPa,峰值应力从32.81 MPa增加到34.48 MPa。当细骨料掺量从30%增加到40%时,7 d应力-应变上升段曲线斜率有所下降。当细骨料掺量从10%增加到20%时,28 d的应力-应变上升段曲线斜率下降,20%细骨料掺量时曲线斜率最小,弹性模量为13.01 GPa。随着细骨料掺量逐渐增加,碱激发砂浆28 d应力-应变上升段曲线斜率上升,说明弹性模量逐渐增加。而砂浆28 d的峰值应力则随着细骨料掺量增加而减小。当掺量从30%增加到40%时,碱激发砂浆7 d峰值应力下降幅度最大,达到了15.60%,28 d的峰值应力下降了6.99%,峰值应变也有所下降,7 d和28 d的峰值应变分别降低了16.04%和3.63%。由于砂浆界面过渡区力学性能较弱,受压容易产生裂纹。随着压应力不断增大,微裂纹逐渐变大且连通,随后表现为破坏开裂,应力出现骤降。随着细骨料掺量增多,单位体积砂浆的胶凝材料含量相对减少,峰值应变减小。龄期增加,应力-应变下降段曲线变陡(参数ad增大),表明砂浆后期变形能力较差,呈现出更显著的脆性破坏。

图11 龄期7 d时不同细骨料掺量砂浆的应力-应变曲线Fig.11 Stress-strain curves of mortar with different fine aggregate content in 7 d
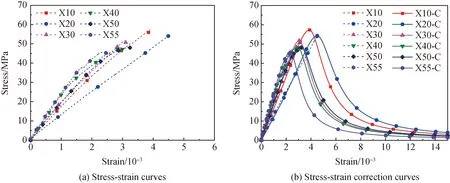
图12 龄期28 d时不同细骨料掺量砂浆的应力-应变曲线Fig.12 Stress-strain curves of mortar with different fine aggregate content in 28 d
3 结 论
(1)矿渣掺量增加有利于提高碱激发矿渣/粉煤灰净浆/砂浆的力学强度,对碱激发矿渣/粉煤灰砂浆峰值应变影响不大。
(2)随着细骨料掺量增加,碱激发矿渣/粉煤灰砂浆28 d的抗压强度和峰值应力逐渐降低,但弹性模量有所增大,在18.72~23.10 GPa之间,砂浆弹性模量相对净浆更高。
(3)基于水泥混凝土受压应力-应变曲线表达式,建立了碱激发矿渣/粉煤灰净浆/砂浆的应力-应变全曲线方程,拟合曲线与试验结果较为吻合。根据拟合结果,当矿渣掺量增加时,净浆/砂浆应力-应变下降段曲线变陡(参数ad增大),表明材料的脆性增强。
