新能源互联电力系统双积分反馈PID 负荷频率控制

张 成，张 艳

（安徽工程大学电气工程学院高端装备先进感知与智能控制教育部重点实验室，芜湖 241000）

新能源发电占比不断增加，使现代电力系统在规模、复杂度和结构上发生了深刻地变化[1-2]，给电力系统频率稳定带来极大的影响[3-4]。为了解决电力系统频率稳定问题，提高电能质量，负荷频率控制LFC（load frequency control）在电力系统中被广泛研究[5-10]。文献[9]针对含光伏发电的两区域互联电网的LFC 问题，提出一种含滤波的PID 控制器，该控制器在参数不确定的情况下仍有较强的鲁棒性和非脆弱性；文献[10]针对传统控制策略无法满足含光伏发电的互联电网实时运行问题，提出一种较为新颖的含滤波系数双积分PID 控制器PIDF-II（PID with filter plus double integral）控制器，使互联电网系统具有较强的鲁棒性。

PID 控制因其具有结构简单、鲁棒性强等优点使用最为广泛[11]。然而在PID 控制算法中比例增益、积分增益和微分增益难以获取，文献[12]针对温控系统的PID 控制器的参数整定复杂问题提出一种基于改进粒子群算法的PID 控制器参数优化算法；文献[13]针对大型中央空调系统的负荷需求多变、能耗较大的问题，提出利用天牛须-粒子群优化BAS-PSO（beetle antennae search-particle swarm optimization）算法来解决上述问题，提高了系统的节能率；文献[14-16]将智能算法引入电力系统的LFC中用以优化PID 控制器参数，将传统PID 控制器的参数整定问题转变成智能算法寻找最优值问题。单一的智能算法很难获得较为优化的控制器参数，文献[17]针对粒子群算法收敛速度慢，容易陷入局部最优问题，提出基于天牛须搜索BAS（beetle antennae search）算法的PID控制器设计方法。相比粒子群算法、灰狼优化算法等，BAS算法在迭代中，每个粒子都会对环境空间进行判断，可以较好的避免局部最优，提高搜索精度。因此将BAS算法引入其他算法中，具有一定的优化效果。

另一方面，电池储能BES（battery energy storage）具有响应速度快、柔性调控能力强等优点，成为新的互联电力系统辅助调频方式。本文将光伏发电、火力发电和储能“捆绑”在一起，构成混合发电系统，用来解决含新能源电力系统的调频难题。首先，建立光、火、储两区域互联电力系统模型，设计出该模型的含滤波系数的双积分反馈PID 控制器PIDF-FII（PID with filter plus feedback double integral controller），提出基于改进天牛须搜索优化的粒子群IBAS-PSO（improved beetle antennae search-particle swarm optimization）算法；然后，对PIDF-FII 控制器进行参数整定；最后，通过数值仿真验证本文所提方法的有效性和优越性。

1 光火储电力系统LFC 模型

为了符合实际电力系统的现状，在混合电力系统中采用多种原动机，光、火、储两区域互联电力系统模型如图1 所示。图1 中，区域1 除了光伏发电模块还包括了非再热式汽轮机发电模块；区域2包含再热式汽轮机发电模块和能够快速调节频率的储能电池模块。

图1 光、火、储两区互联电力系统模型Fig.1 Model of solar-fire-storage two-area interconnected power system

在两区域互联电力系统中，LFC通过区域控制偏差ACE（area control error），实现对本区域的频率偏差和相邻区域间的联络线交换功率的控制，使稳定状态下的系统频率偏差和联络线功率偏差等于零(Δf1=Δf2=ΔPtie=0)。区域1 和区域2 的频率偏移因子B1、B2，以及控制器输出信号u1、u2通过调速器参数R1、R2与对应区域的频率偏差进行比较。系统通过控制器对调速器和原动机的间接控制，实现系统的LFC。其中，Tg1、Tg2为调速器时间常数；Tr1、Tr2为汽轮发电机时间常数；M1、M2为机组惯性时间常数；Tr、Kr分别为再热器时间常数和再热器增益；D1、D2为机组阻尼时间常数；T12为联络线时间常数；Ppv为光伏组件的输出功率；PB为电池的输出功率。

1.1 光伏模型

在电力系统的控制问题中，由光伏板、最大功率点跟踪MPPT（Maximum Power Point Tracking）控制器、逆变器和滤波器组成的光伏系统，可用惯性环节表示其等效的传递函数[18-19]，即

式中，A、B、C、D分别为传递函数中分子和分母多项式的系数。

1.2 电池模型

在区域2 中，本文采用电池储能进行二次调节，解决因新能源发电并网而导致的电力系统频率不稳定、低抗扰性和弱支撑性问题。当BES系统用以调频研究时，跟踪控制信号对于BES过程有一定的响应时间，其电池模型[20-21]可表示为

式中：Kb为储能电池的单位调整系数；Tb为储能电池的延迟时间常数。

2 PIDF-FII 设计

针对光伏并入电网引起的电力系统鲁棒性降低、电压频率不稳的问题，根据文献[9-10]设计出PIDF-FII，用来解决光、火、储两区域电力系统的LFC问题。

PIDF-FII结构如图3所示。其中，KPi、KIi、KDi、Nai、KIIi，（i=1，2）分别为区域1和区域2控制器的比例增益、积分增益、微分增益，滤波系数和双积分反馈增益。滤波系数效果上如同低通滤波器，能够减少电力系统中高频传感器噪声及系统振荡。本文将双积分反馈增益KIIi与一个积分环节相连，构成一个负反馈系统，当区域控制误差信号通过这个负反馈时，使区域控制误差信号减弱，从而提高控制器灵敏度，有利于减小系统超调，使系统稳定。

3 光、火、储两区域电力系统LFC 策略

本节通过提出IBAS-PSO 算法，给出光、火、储两区域电力系统LFC策略。

3.1 改进的BAS 算法

BAS 算法原理：当天牛个体在觅食时，它们能够通过头上的触角感受到食物气味的强弱；当天牛左侧的触角感受到的食物的气味强于右侧触角，天牛就会往左侧飞去，反之向右飞。文献[22]给出了BAS算法的具体步骤。

为增强BAS算法的精确性，减缓BAS算法搜索方向的幅度改变量，本文在天牛触角的搜索方向上引入方向改变因子α，用来调节BAS算法中天牛触角的随机搜索方向，提出改进的天牛须搜索IBAS（improved beetle antennae search）算法，其具体步骤如下：

步骤1模拟搜索行为。假设天牛的触角在N维空间中的位置是X=(x1,x2,x3,…,xn)，则搜索的随机方向可表示为

式中，rand（）为随机函数。

步骤2通过模拟天牛觅食原理，分别向区域左和区域右搜索，所搜索的位于左边区域和右边区域可表示为

式中：Xk为天牛第k次迭代后的位置，即在D维空间中，第k次迭代后触角的位置；dis为触角间的距离。

步骤3更新天牛的位置。基于步骤2 的搜索，进行位置更新，新位置Xk+1可表示为

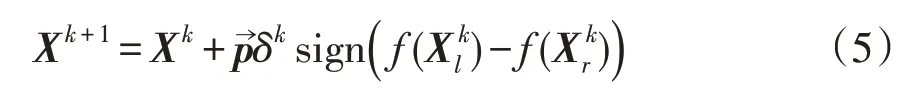
式中：δk为第k次迭代的步长；sign（）为符号函数；f（）为优化函数。

3.2 IBAS-PSO 算法

为了将IBAS 算法用于优化PSO 算法的更新公式中，本文提出一种IBAS-PSO 算法，其流程如图3所示。图3 中，kmax为最大迭代次数；Fit 为算法迭代中的适应度值；minFit为最小适应度值；方向改变因子α=Fit-min Fit。

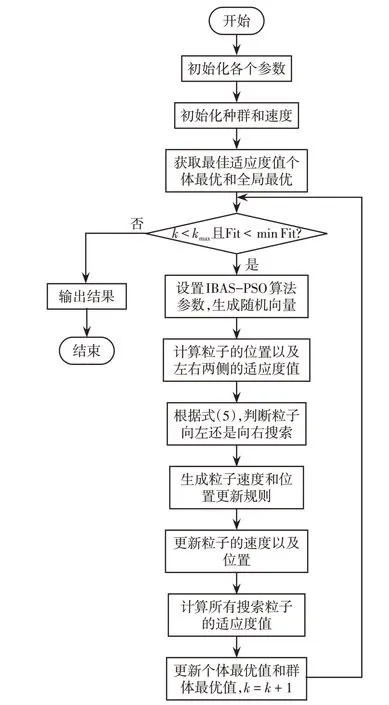
图3 IBAS-PSO 算法流程Fig.3 Flow chart of IBAS-PSO algorithm

IBAS-PSO 算法的速度和位置更新公式可表示为

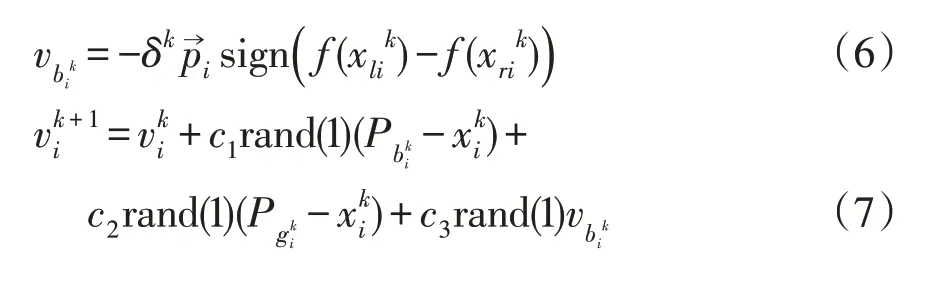
相较于已有的BAS改进PSO算法[23-24]，本文所提出的IBAS-PSO 算法引入了方向改变因子α，即每次迭代，粒子自身都会基于左右两侧的适应值，对环境进行选择和独立判断；调整方向改变因子α，选取合适的方向，再对粒子进行位置和速度更新。这使算法收敛所需要的时间较短，所需的迭代次数也相应减少，大大克服了传统粒子群收敛速度过快和容易陷入局部最优的缺点。

3.3 基于IBAS-PSO 算法的光火储两区域电力系统LFC

在图2 的光、火、储两区互联电力系统中，为了使区域1和区域2中的系统频率偏差及联络线中的交换功率偏差尽可能的减弱，实现功率平衡，保证电能质量，本文采用联络线偏差控制TBC（tie-line bias control）模式，则第i区的ACEi可表示为

图2 i 区PIDF-FII 结构Fig.2 PIDF-FII controller in Area i

式中：K为频率偏差系数，；Δfi为第i区的频率偏差；为第i区和第j区之间的联络线功率偏差。

负荷频率控制输入ui可表示为

LFC的性能指标JITAE可表示为

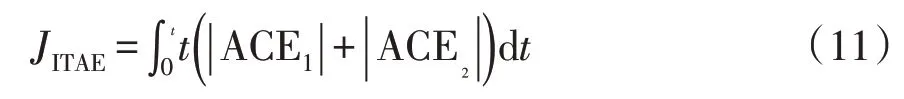
式中，t表示时间。采用时间与误差绝对值积的积分ITAE（integral of time multiplied by the absolute value of error）作为性能指标，不仅能够消除各区域下的系统频率误差和功率振荡，还可以抑制控制器内长时间存在的部分误差，从而获得调节器最佳整定参数值[25]。

将图2中第i区域的PIDF-FII控制器增益KPi、KⅠi、KDi、Nai、KⅡi（i=1，2）作为“天牛”粒子，即X=(KP1,KⅠ1,KD1,KⅡ1,Na1,KP2,KⅠ2,KD2,KⅡ2,Na2)，由 第3.2节提出的基于IBAS-PSO算法，对“天牛”粒子即向量X的元素进行相应的迭代，更新位置和速度，使粒子达到最优的位置。

4 数值仿真

为验证所提光、火、储两区域互联电力系统LFC 策略的有效性和优越性，从PIDF-FII 控制器设计、IBAS-PSO 算法性能测试和基于IBAS-PSO 算法的光、火、储两区域电力系统LFC 的动态响应等方面进行仿真分析。

4.1 控制器性能分析

在光、火、储两区域互联电力系统中，采用IBASPSO 算法对PIDF-II 控制器[10]和本文所提PIDF-FII控制器参数进行整定。在运用IBAS-PSO算法时选取种群规模N=100；最大迭代次数kmax=100；惯性因子W=0.6；适应度值Fit为LFC的性能指标JITAE，最小适应度值minFit=0.1。参数的搜索范围设定为KPi、KⅠi、KDi∈[0，50]；滤波系数Nai∈[0，500]；KⅡi∈[0，0.2]，i=1，2。控制器整定的参数见表1。

表1 基于IBAS-PSO 算法的控制器整定的参数Tab.1 Tuning parameters of controller based on IBASPSO algorithm

在Simulink仿真中，仿真时间设定为30 s，为了模拟环境、光照等因素对光伏发电的影响，当t=10 s时，在区域1中加入阶跃扰动；当t=20 s时，在区域2 中加入阶跃扰动，模拟负荷变化对整个系统的影响。两种控制器得到的频率偏差和联络线功率偏差如图4～6 所示。由图4～6 可知，当在第10 s 和第20 s 发生扰动时，相较于PIDF-II 控制器的调节能力，PIDF-FII 控制器的超调量更小，即系统的调节能力更好，具有更有效的抑制系统偏差能力和处理外界扰动能力。

图4 不同控制器下的区域1 的频率偏差Fig.4 Frequency deviation in Area 1 under different controllers

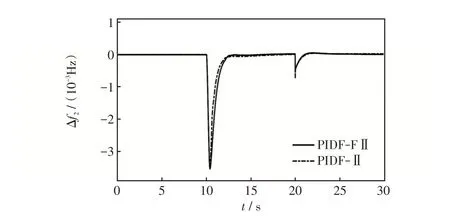
图5 不同控制器下的区域2 的频率偏差Fig.5 Frequency deviation in Area 2 under different controllers

图6 不同控制器下的联络线交换功率偏差Fig.6 Tie-line exchange power bias under different controllers

4.2 算法性能测试

在算法方面，使用CEC2013 benchmark[26]基本测试函数Schwefel's problem 22函数f1(X)和含噪声的Quaratic 函数f2(X)用于IBAS-PSO 算法、BAS 算法和PSO 算法的性能比较，数据见表2。f1(X)、f2(X)可表示为

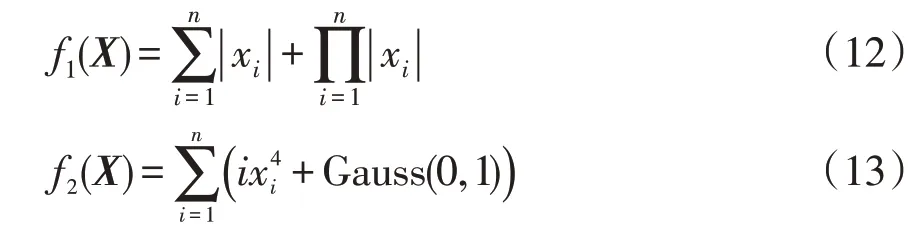
式中：xi为n维向量X的元素；Gauss（0，1）为期望值为0、方差值为1的高斯噪声。

由表2 数据可知，与BAS 算法和PSO 算法相比，IBAS-PSO算法得到的最优值、平均值和最差值均优于BAS 算法和PSO 算法；平均值和最差值与BAS算法和PSO算法的数值相差了2～3个数量级。

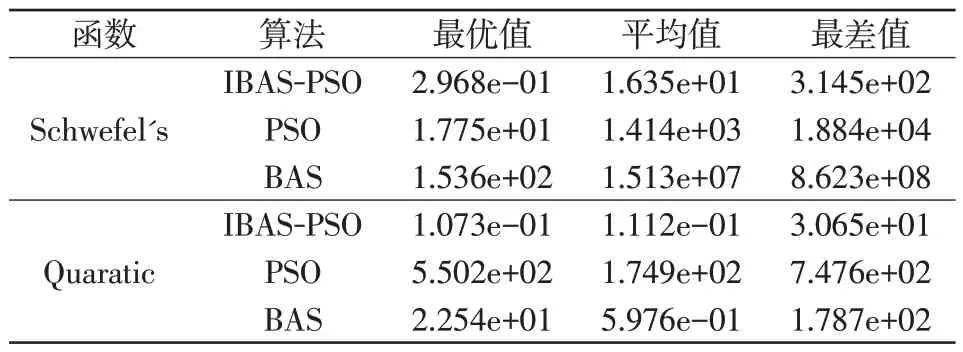
表2 测试函数性能分析Tab.2 Performance analysis of test functions

4.3 算法寻优及动态性能分析

为了进一步验证IBAS-PSO 算法优越性，分别采用IBAS-PSO 算法、BAS 算法和PSO 算法对光、火、储两区域互联电力系统FLC的PIDF-FII控制器进行参数整定。两区域互联电力系统的区域1 和区域2频率偏差、ACE和联络线功率偏差如图7～11所示。

图7 不同算法下的区域1 频率偏差Fig.7 Frequency deviation in Area1 under different algorithms

图8 不同算法下的区域2 频率偏差Fig.8 Frequency deviation in Area 2 under different algorithms

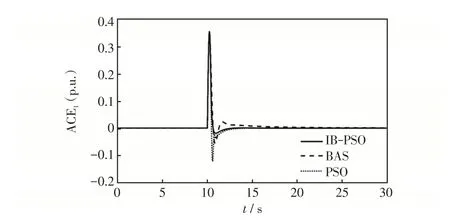
图9 不同算法下的区域1ACEFig.9 Area control error in Area 1 under different algorithms

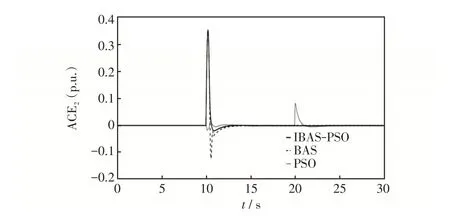
图10 不同算法下的区域2ACEFig.10 Area control error in Area 2 under different algorithms

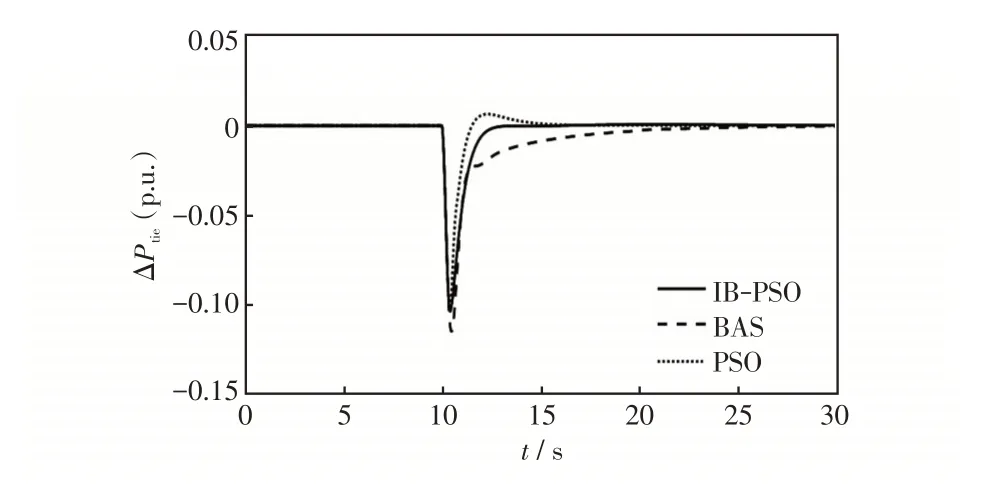
图11 不同算法下的联络线交换功率偏差Fig.11 Tie-line exchange power bias under different algorithms

由图7～11 可知，与BAS、PSO 算法相比，IBASPSO 算法优化的控制器可以在最短的时间内使波动的系统频率偏差、ACE和联络线功率偏差迅速恢复稳定，超调量也显著下降，系统震荡次数相对较少。可见IBAS-PSO算法有很好的抗干扰能力和更好的全局搜索能力。

在PIDF-FII 控制器下3 种算法收敛曲线如图12所示。由图12可知，BAS 算法的收敛效果较差；PSO 算法和IBAS-PSO 算法的最小适应度值较为接近。但IBAS-PSO算法在第10次迭代就进入收敛状态，而PSO 算法在第18 次迭代才进入收敛。可见IBAS-PSO 算法具有收敛时间较短，迭代次数少的优点。

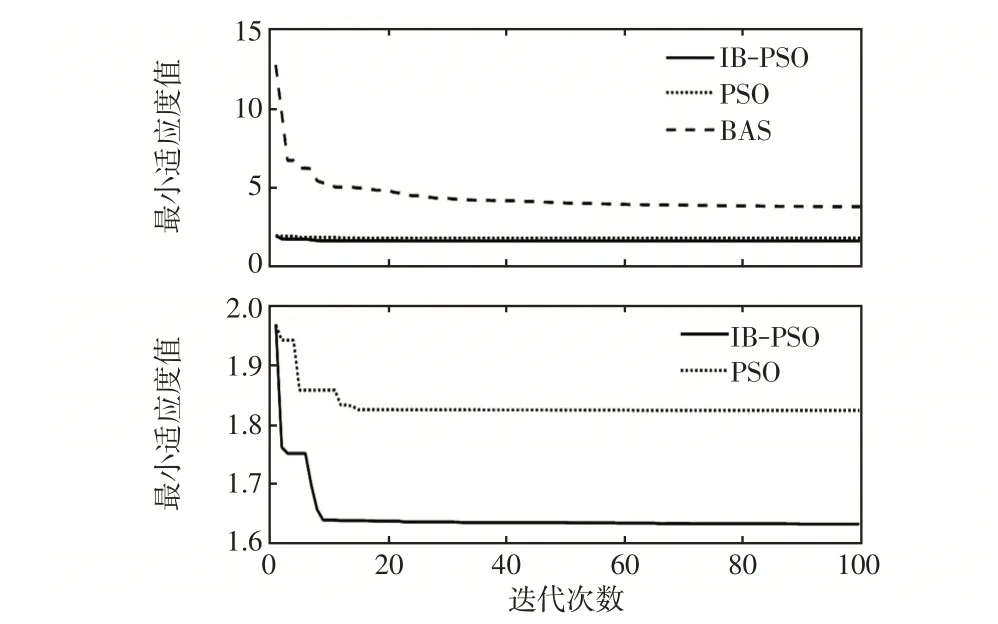
图12 PIDF-FII 控制器下3 种算法收敛曲线Fig.12 Convergence curves of three algorithms under PIDF-FII controller

5 结语

针对含光伏发电的光、火、储两区域电力系统的频率调节问题，本文提出了一种基于IBAS-PSO算法优化的PIDF-FII控制策略。首先，通过在不同区域加入扰动模拟环境、光照等因素使光伏发电和负荷发生变化对整个系统产生影响；采用IBASPSO 算法分别对PIDF-FII 控制器和PIDF-II 控制器的参数进行整定，给出互联电力系统中的频率偏差和联络线功率偏差曲线图；仿真曲线表明，基于IBAS-PSO算法下PIDF-FII，具有更好的抑制系统频率波动和振荡能力。然后，采用CEC2013 benchmark 中的Schwefel's 函数和Quaratic 函数分别对BAS算法、PSO算法和本文所提的IBAS-PSO算法进行算法测试，测试结果表明，采用IBAS-PSO算法得到的最优值、平均值和最差值均优于BAS 算法和PSO算法。最后，分别用IBAS-PSO算法，BAS算法和PSO算法对PIDF-FII控制器进行参数整定，进一步验证IBAS-PSO算法的优越性。