基于主从博弈的配电网分布式电源电能定价

2022-11-01彭依明

电力系统及其自动化学报 2022年10期

肖健，钏星，彭依明，陈波

（1.广东电网有限责任公司广州供电局，广州 510000；2.南方电网数字电网研究院有限公司，广州 510700）

分布式电源在配电网中的高渗透率接入，促进了清洁能源的利用，提升了配电网的运行经济性[1]。同时，分布式电源的间歇性也给配电网的安全运行带来了挑战[2]。通过有效调度分布式电源出力，可以在保证配电网安全、经济运行的同时，促进分布式发电消纳。

分布式电源可以分为可再生能源发电分布式电源RDG（renewable distributed generation）和不可再生能源发电分布式电源NDG[3]（non-renewable distributed generation）。以风电，光伏为典型代表的RDG具有发电成本低、清洁无污染等特点[4]，但其有功出力受到环境因素限制[5]，仅可通过功率削减进行有功出力调度[6]。凭借零碳及低成本优势，RDG在分布式电源中的占比逐步提升[7]。以微型燃气轮机为代表的NDG 也采用变流器并网[8]，其发电边际成本随机组出力增大而提升，可实现计划出力调度，支撑配电网的调度策略[9]。如何有效协调两类分布式电源调度策略，促进配电网的安全经济运行成为有待解决的问题。

随着电力市场改革的推进，新的市场主体不断涌现[10]。分布式电源作为主体与配电网进行电能交易，并获取交易利润[11]，可促进分布式电源的投资规划；配电网通过节点电能定价，可引导分布式电源的交易策略，协调全网分布式电源的出力计划，进而支撑配电网的安全经济运行。

在多利益主体参与的电能交易中，主从博弈（Stackelberg game）模型已被广泛应用于以节点定价的电能交易方法[12]中。文献[13]验证了基于主从博弈的多主体电能交易方法可以同时满足各方的利益需求；文献[14]提出一种基于节点边际定价的配电市场出清方法，将批发市场的交易定价与配电网的节点边际定价问题转化为双层主从博弈问题，并采用库恩塔克KKT（Karush-Kuhn-Tucker）条件及强对偶原理将模型处理为单层博弈均衡约束数学规划问题进行求解；文献[15]提出一种基于主从博弈的运营商电价激励方案，建立运营商和用户的主从博弈模型，优化园区运营商设备出力并引导用户用能行为，实现主从双方的利益共赢。但在多数研究中，没有考虑分布式电源无功调度对于电能交易的支撑作用。

考虑到无功功率调节对配电网电压控制[16]及阻塞缓解的作用，分布式电源可为配电网提供无功辅助服务[17]。文献[18]提出基于变流器并网的分布式电源有功、无功出力独立调节方法，并应用于配电网电压控制中；文献[19]提出一种含分布式电源的配电网动态无功优化调度方法，以解决无功调节中的时空耦合性问题。目前，在多数研究中，无功辅助服务主要用于有功交易方案确定后的无功优化控制，无法实现有功、无功调度的协调[17]。文献[20]进一步提出了考虑光伏出力削减的分布式电源无功辅助服务方法，并应用于配电网的鲁棒优化。因此，在配电网中通过调度RDG、NDG 的无功出力，对缓解系统阻塞，支撑低成本电能交易方案的实现具有良好的应用前景。

基于上述背景，本文综合考虑配电网与分布式电源之间的博弈问题及分布式电源无功辅助服务，提出基于主从博弈的配电网分布式电源日前电能定价方法，主要工作如下。

（1）在异构分布式电源高渗透率接入的背景下，提出基于主从博弈的配电网分布式电源日前电能定价方法，协调了分布式电源最优交易策略和配电网的安全、经济调度问题。

（2）提出与配电网有功交易定价策略紧密协调的分布式电源无功辅助服务方法，该方法可以缓解系统阻塞，支撑有功电能交易的进行，提升系统运行经济性。

（3）利用KKT 最优性条件与强对偶原理，将配电网与分布式电源之间的主从博弈问题转化为混合整数二阶锥规划问题，实现了博弈均衡的快速求解。

1 分布式电源调度模型

在配电网中，考虑到RDG 和NDG 的成本特性差异，配电网对两类分布式电源的消纳策略有所区别。两类分布式电源根据配电网的消纳策略及自身交易利润，制定不同的调度方案。

1.1 RDG 调度模型

以风电、光伏为典型代表的RDG，由于其发电成本较低，通常不考虑这部分成本[9]。为促进可再生清洁能源的消纳，配电网按照固定的上网电价消纳RDG 发出的有功电能[21]。RDG 与配电网的有功电能交易收益可表示为

由于不计RDG 的发电成本，因此RDG 按照最大功率发电可以实现最高收益，但考虑到配电网的安全运行约束，RDG不能始终按照最大功率向配电网供电，且配电网无法通过电能定价引导RDG 的出力计划。因此，RDG的有功发电量交由配电网调度，并依据上网电价结算运行收益。

RDG 的无功出力不产生成本，不作为RDG 的调度资源，交由配电网进行调度并由配电网支付一定的无功调度费用。

1.2 NDG 调度模型

以微型燃气轮机为代表的NDG，其发电效率与发电功率相关。NDG 的发电边际成本随着机组出力增加而递增，目前多数研究常采用二次成本函数对NDG 发电成本进行成本量化。考虑到机组的实际成本特性可能无法通过二次函数精确拟合，可通过分段线性化成本函数描述NDG 的实际发电成本，即

式中：ΩK,i为节点i处NDG发电成本分段线性化的分段集合；ΩT为交易日的交易时段集合；为t时段节点i处NDG的发电成本；为t时段节点i处NDG 的有功出力；ak,i、bk,i分别为NDG 分段线性成本函数第k分段的斜率和截距；μk,i,t为分段线性约束条件的对偶变量。

配电网可以通过交易价格引导NDG 的出力策略。NDG 也可以根据交易价格，进行自主决策，获得最高的交易利润，其目标函数可表示为

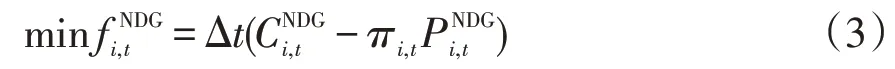
NDG在基于交易价格进行最优调度决策时，需要考虑机组出力约束，其约束可表示为

NDG的无功出力不影响其运行成本，因此不作为NDG 的调度资源，交由配电网进行调度并由配电网支付一定的无功调度费用。

2 配电网电能定价方法

为实现配电网的安全、经济运行，通过对NDG进行日前电能定价，引导NDG 出力策略，并决策RDG 的消纳比例以降低总运行成本。通过日前调度分布式电源无功出力计划，可使配电网进一步缓解系统阻塞，降低系统损耗，抑制电压越限，从而支撑低成本交易方案的实现。

2.1 配电网电能定价模型

配电网以电能成本最低为目标，与上级电网及分布式电源进行电能交易。其目标函数可表示为

考虑到以智能软开关SOP（soft open point）为代表的柔性电力电子设备接入提升了配电网的调度灵活性，配电网可以通过调度SOP支撑配电网与分布式电源电能交易的进行。

配电网的潮流约束可表示为

式中：Ωb为配电网支路集合；Pji,t、Qji,t分别为t时段支路ji传输的有功和无功功率；Pik,t、Qik,t分别为t时段支路ik传输的有功和无功功率；Rij、Xij分别为支路ij的电阻和电抗；Iij,t为t时段支路ij传输的电流；Ui,t、Uj,t分别为t时段节点i和节点j电压幅值；Pi,t、Qi,t分别为t时段节点i净注入有功和无功功率；分别为t时段节点i分布式电源注入的总有功和无功功率；分别为t时段节点i的负荷有功和无功功率；分别为SOP在t时段节点i注入的有功和无功功率。

配电网的系统安全运行约束可表示为

式中：Umax、Umin分别为节点i电压上、下限，分别为支路ij的电流幅值上、下限。

配电网可以调整两类分布式电源的无功出力，并决定RDG 有功发电量的消纳比例。通过调度分布式电源的无功出力，支撑有功电能交易的进行，缓解配电网阻塞和运行问题。

配电网对分布式电源的调度约束可表示为

分布式电源变流器通常由分布式电源运行商投资建设，因此可将配电网通过调度分布式电源无功出力实现的成本降低额按照分布式电源无功出力占比分配给分布式电源运行商；同时，配电网自身保留部分无功调节利润。

SOP作为配电网的调节资源，同样可以通过调节有功和无功潮流分布，支撑有功电能交易的进行，为成本更低的交易方案提供可行性。SOP运行约束可表示为

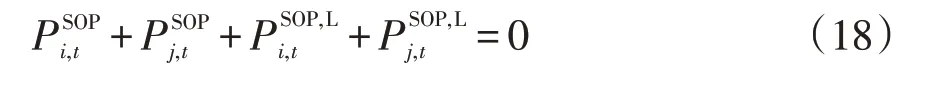
2.2 单层博弈均衡约束定价模型转化

配电网作为博弈领导者制定与NDG的交易电价，通过引导NDG 的交易策略，降低配电网运行成本。NDG作为博弈跟随者，根据配电网的电能定价，制定最优的发电计划。在这一主从博弈过程中，配电网需根据NDG 反馈的调度计划调整电能定价，并决策RDG 的消纳策略，以实现配电网电能成本的降低。本文将跟随者NDG 调度问题作为下层问题，领导者配电网电能定价问题作为上层问题，基于主从博弈的配电网分布式电源电能定价架构如图1所示。

图1 基于主从博弈的配电网分布式电源电能定价架构Fig.1 Electricity pricing framework for distribution network with DGs based on Stackelberg game

通过将NDG 的最优调度问题转化为配电网电能定价问题的约束条件，可实现从双层主从博弈模型到单层博弈均衡约束定价模型的转化，从而实现博弈均衡问题的数学求解。

在下层问题中，按节点i的NDG调度最优性条件求拉格朗日函数各偏导数为零，即

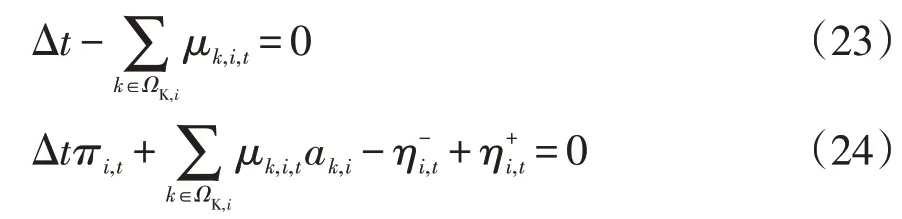
在下层节点i的NDG 调度最优性条件中，互补松弛条件可表示为

式中，“⊥”表示两式乘积为零，即两侧表达式至少一侧等于0。

将各节点NDG 调度问题的最优性条件添加到上层配电网电能定价模型中，可得单层博弈均衡约束定价模型为

3 混合整数二阶锥规划模型转化

配电网单层博弈均衡约束定价模型包含大量非线性约束，其对模型的求解带来困难。通过线性化与凸松弛技术，可以进一步将式（28）转化为混合整数二阶锥规划模型，保证模型的求解速度及收敛性。

3.1 配电网运行约束凸松弛

式（14）～（17）的分布式电源调度约束可处理为旋转锥约束，即

式（18）～（21）的SOP运行约束可松弛处理为

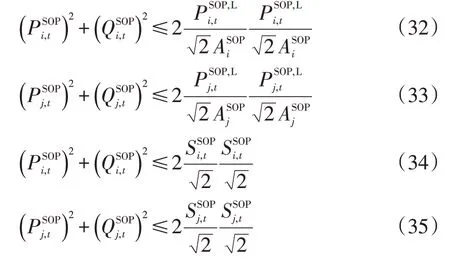
通过式（29）～（35）将配电网运行约束转化为标准二阶锥规划模型约束。

3.2 下层模型最优性条件线性化

在下层NDG 调度问题的最优性条件中，互补松弛条件包含变量的非线性乘积项，可以通过大M法进行线性化处理。

节点i的NDG 调度问题的互补松弛条件可转化为

式中：M为一个足够大的正数；为对应不等式约束互补松弛条件线性化引入的二进制变量，取值0或1。

3.3 博弈均衡约束定价模型目标函数线性化

通过整理强对偶方程可得

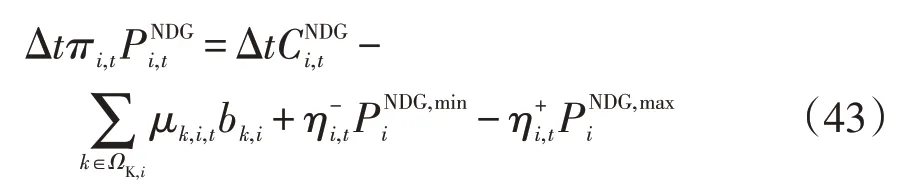
单层博弈均衡约束节点定价模型的目标函数可表示为

将式（44）进行模型转化及线性化处理，配电网最优电能定价与分布式电源最优调度之间的主从博弈问题被转化为混合整数二阶锥规划模型，即

式（45）的混合整数二阶锥规划模型为凸规划问题，保证了模型最优解的存在性，可以通过商业求解器CPLEX进行高效求解。

4 算例测试

4.1 改进IEEE 33 节点配电网算例

测试算例基于IEEE 33节点配电系统算例进行改造，配置部分有RDG、NDG 和1个两端口SOP，保障交易的灵活进行。改进IEEE 33节点算例的拓扑结构、支路阻抗参数、节点负荷参数与IEEE 33节点标准算例保持一致；电压等级为12.66 kV，负荷总有功功率需求和总无功功率需求分别为3.175 0 MW和2.300 0 MVar；系统电压基值设定为12.66 kV，功率基值设定为1 MVA。改进IEEE 33节点配电系统结构如图2所示。

图2 改进IEEE33 节点配电网算例结构Fig.2 Topology of example of modified IEEE 33-node distribution network

上级电网分时电价如图3所示；RDG配置位置及参数如表1 所示；NDG 配置位置及参数如表2 所示；风机、光伏及负荷日运行曲线如图4所示；RDG上网电价[21]设定为0.415 3¥/（kW·h）。本算例中，NDG类型为微型燃气轮机，其成本函数设定为二次函数，并均分为15 段进行分段线性化处理。一日分为24个交易时段，每时段时长为1 h。

图3 上级电网电价Fig.3 Electricity trading price with upper grid

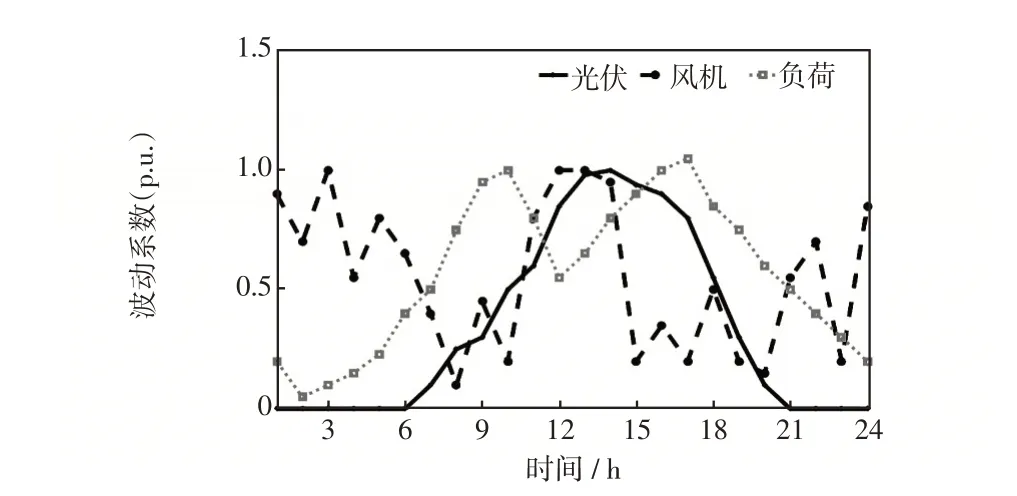
图4 RDG 出力及负荷曲线Fig.4 Operation curves of output from RDGs and load

表1 RDG 接入位置及容量Tab.1 Installation positions and capacities of RDGs

表2 NDG 接入位置及容量Tab.2 Installation positions and capacities of NDGs

为了验证所提出的基于主从博弈配电网分布式电源电能定价方法的可行性及有效性，假设分布式电源保持并网运行，并采取如下3种场景进行对比分析。

方案1RDG、NDG保持上网功率为零，配电网仅与上级电网交易，作为各方运行收益参考基准。

方案2配电网与RDG、NDG 采用本文所提出的电能定价方法仅进行有功电能交易，分布式电源功率因数设定为1，假定线路6～26及其后续线路电流容量为电流基值的1.25倍。

方案3配电网与RDG、NDG 采用本文所提出的电能定价方法进行有功及无功电能交易，配电网将分布式电源无功调度利润的50%按无功出力比例分配给分布式电源，假定线路6～26 及其后续线路电流容量为电流基值的1.25倍。

4.2 结果分析

方案2、3 的配电网对NDG 的电能定价如图5所示。由图5可以看出，配电网对不同发电成本的NDG电能定价较为相近，多数时段定价低于上级电网电价，以降低配电网自身运行成本。在17 时方案2的定价结果中，配电网对NDG 3的电能定价显著高于方案3，这是由于线路6～26 发生阻塞，需要调度NDG 3以较高的出力抑制线路过载，导致交易价格提升。

图5 方案2、3 电能定价Fig.5 Electricity trading price in Schemes 2 and 3

方案2、3 的配电网与两类分布式电源的有功交易结果如图6所示。其中，由于RDG上网电价较低，使方案2、3配电网调度结果中的RDG始终以最大功率上网；17 时配电网与NDG 的交易结果进一步验证了分布式电源无功调度对于缓解系统阻塞的作用。

图6 方案2、3 有功交易功率Fig.6 Active power trading results in Schemes 2 and 3

方案2、3的分布式电源运行收益结果如图7所示。由于RDG 不计发电成本，从而在与配电网的电能交易中获得了较高的收益。RDG 通过响应配电网的无功调节获得利润分成，使RDG在方案3中相对于方案2 获得了一定收益提升。在图7（a）有功交易中，NDG 3 响应配电网的高电能定价，提升出力，缓解系统阻塞并获取较高利润；在图7（b）中，配电网通过调度分布式电源无功即可有效缓解阻塞问题，并将系统成本降低量的50%按无功出力比例分配给各分布式电源，促进了分布式电源的利润提升和配电网的经济运行。

图7 方案2、3 分布式电源运行收益Fig.7 Operation profits of DGs in Schemes 2 and 3

方案2、3的分布式电源的无功调度结果如图8所示。RDG在方案2、3中均不存在有功削减，时段为3、12、13时，风机有功出力达到容量上限，从而无功出力为0。光伏也因在14时达到有功出力上限，限制了无功出力。在图8（a）中，NDG3在17时的无功出力较大，以减少线路5～26上的无功传输，缓解系统阻塞，促成了对全系统更为经济的交易方案。

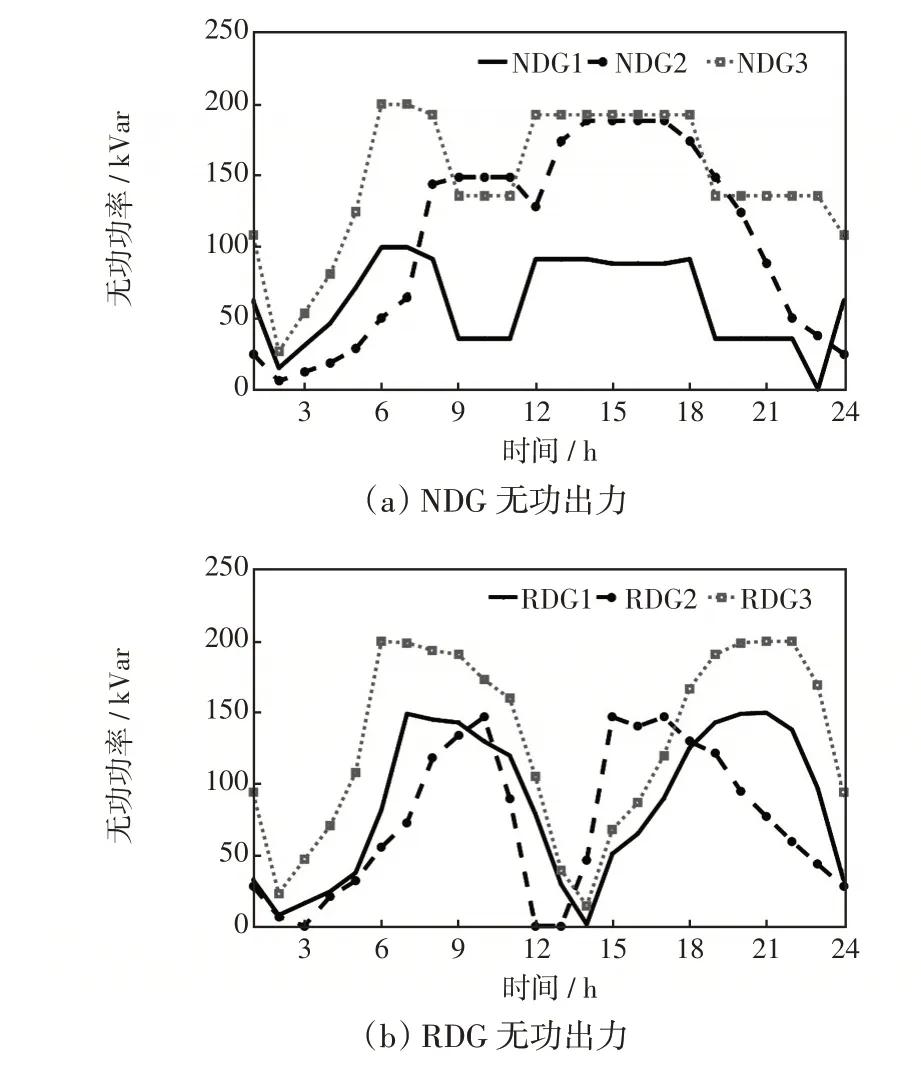
图8 方案3 分布式电源无功出力调度结果Fig.8 Reactive power output scheduling results of DGs in Scheme 3

方案2、3 相对于方案1，配电网各时段的成本降低情况如图9所示。通过与分布式电源交易，配电网可以显著降低自身运行成本。方案3 相对于方案2，配电网通过调度分布式电源无功出力在17时有效缓解了阻塞问题，进一步降低了系统运行成本；在17时以外的各时段中，通过分布式电源无功调节，配电网减少了无功功率传输，并减少系统损耗带来的电能成本；在一天中，分布式电源无功调节使配电网成本降低了282.54 ¥，在此部分收益中，配电网自身保留50%。

图9 方案2、3 中配电网成本降低Fig.9 Cost reduction of distribution network in Schemes 2 and 3

方案3 中SOP 的有功、无功功率调度结果如图10 所示。图10（a）为SOP 在节点12 注入的有功功率，与节点22 处SOP 消耗的功率近似相等。通过SOP 对有功功率的空间转移，降低系统阻塞风险，并减少有功在长距离交流线路上传输的损耗。由图10（b）可以看出，重负荷时段SOP在节点12注入无功，以减少无功功率在系统中的长距离传输，并降低系统损耗；而节点22与源节点电气距离较近，且分布式电源无功出力已有效减少了支路上的无功传输，无需SOP进行无功调节。