基于干扰观测器的时滞非线性切换系统滑模控制方法

黄丽琼，王园园

(1.商洛学院数学与计算机应用学院，陕西 商洛 726000;2.商洛学院电子信息与电气工程学院，陕西 商洛 726000)

0 引言

时滞非线性切换系统广泛应用于能源环境、系统和控制科学等多个领域[1]。时滞非线性切换系统是由一些子系统通过特定切换规则组合而成的混合系统[2]。根据切换规则，其各子系统均能够在瞬时沿着系统轨迹被激活，因此各子系统的控制非常重要[3]。时滞非线性切换系统搭建了不确定或复杂系统与连续线性系统之间的桥梁，意味着该系统的控制具备二者共同的特性[4]。

目前，时滞非线性切换系统控制的相关研究已经取得了很多成果，包括保成本控制、自适应控制和稳定性分析等[5]。在多种控制方法中，滑模控制由于其固有的瞬态性能好、响应速度快和易实现等优势，以及对于外部扰动具备鲁棒性、对于参数而言具有不确定性等特征而获得了广泛应用。特别是在时滞非线性切换系统中，滑模控制一直是一种应用很多的控制方法。在该背景下对时滞非线性切换系统滑模控制方法进行研究。现综合所取得的研究成果，应用干扰观测器设计一种时滞非线性切换系统滑模控制方法。

1 时滞非线性切换系统滑模控制方法设计

1.1 系统建模

构建时滞非线性切换系统模型[6]。具体为

(1)

x2为系统状态向量-姿态角速率；x1为系统状态向量-姿态；y为系统输出向量；d为未知的外部干扰；sat(u)为系统输入向量u的饱和函数[7]。

1.2 设计切换干扰观测器

针对系统在发生结构变化时会发生复合干扰变化的情况[8]，设计一种非线性切换干扰观测器实施其不连续干扰的估计。非线性切换干扰观测的设计具体如下所述。

对于式(1)系统，定义为

(2)

vn为第n个定义值[9]。

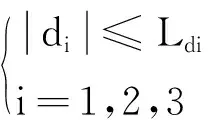
(3)

bd(n-i)为参数函数；n为正整数。

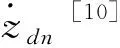
(4)

hσ(t)为非线性切换干扰观测器增益。通过求导后的中间变量，设计干扰观测器的形式，具体为

(5)

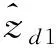
1.3 设计切换滑模控制器

结合设计的切换干扰观测器，通过Backstepping方法，设计一种切换滑模控制器。依据标量非线性特性设计1个滑模面，并提出一种滑模控制器算法，使时滞非线性切换系统能够满足设计滑模面的实际可达性条件，完成切换滑模控制器的设计，实现系统的滑模控制[13]。

设计的滑模面s(k,i)具体为

(6)

k为正整数；k0为加权指数；x(l)为第l个控制自变量；G(i)为滑模设计阈值函数；A(i)、B(i)为理想滑模函数；K(i)为函数变量[14]。

设计的滑模控制器算法能够使时滞非线性切换系统轨迹在设计的切换滑模控制器下，在有限时间达到滑模面[15]。具体为

(7)

w(k,i)为标量非线性特征函数；Ω为正定函数[16]；s(k,i)为系统轨迹；F(s(k,i))为系统轨迹左右乘函数；ρ(k,i)为到滑模面的轨迹；ω为切换信号。根据上述过程，实现基于干扰观测器的时滞非线性切换系统滑模控制。

2 实验研究

2.1 实验准备

对于设计的基于干扰观测器的时滞非线性切换系统滑模控制方法，进行实验测试。实验中选择的时滞非线性切换系统为一种变后掠翼NSV，其飞行环境复杂，工作任务繁杂，并且飞行包络极大，因此表现出严重耦合性、快速时变性、高度非线性以及强烈的不确定性，对于系统的滑模控制有着很高的要求。

实验时滞非线性切换系统的控制舵面包括方向舵、副翼左右升降舵、水平鸭翼，分别位于垂直尾翼、三角副翼尾部和机体前部。实验中，其操作舵面实际偏转角变化范围定为-30°～30°。通过操作舵面控制其飞行变形，其飞行变形过程具体如下：在亚声速阶段水平鸭翼展开，通过舵面偏转角在俯仰方向产生控制力矩，在其他阶段将水平鸭翼收回机体内部。

在飞行变形过程中，亚声速时机翼后掠角为40°，高超声速时机翼后掠角为75°，超声速时机翼后掠角为60°。实验时滞非线性切换系统的飞行参数具体为：在机翼后掠角分别为75°、60°、40°时，翼展长度分别为18.32 m、41.11 m、54.90 m；平均气动弦长分别为24.38 m、23.16 m、18.29 m；左、右升降舵弦长分别为2.22 m、2.22 m、2.22 m；左、右升降舵面积分别为8.59 m、8.59 m、8.59 m；方向舵展长分别为6.97 m、6.97 m、6.97 m；方向舵面积分别为15.01 m、15.01 m、15.01 m。

在飞行变形过程中，通过设计的基于干扰观测器的时滞非线性切换系统滑模控制方法对其实施滑模控制实验。

在实验中，对其运动过程作出以下假设：认为变后掠翼NSV的变形运动是理想刚体运动，不考虑控制舵面与机身弹性模量、强度和刚度等方面的变化；假设实验中周围的大气是干洁与均匀的；忽略操纵舵面与液体燃料的转动惯量与晃动。

2.2 切换信号实验

在实验中，首先测试切换信号，具体如图1所示。在切换信号下实施滑模控制实验。

图1 切换信号实验结果

2.3 切换信号跟踪实验

实验时，利用本文设计方法跟踪时滞非线性切换系统切换信号，测试跟踪过程中系统的姿态角与姿态角速率实验数据。

跟踪过程中的姿态角数据，如表1所示。

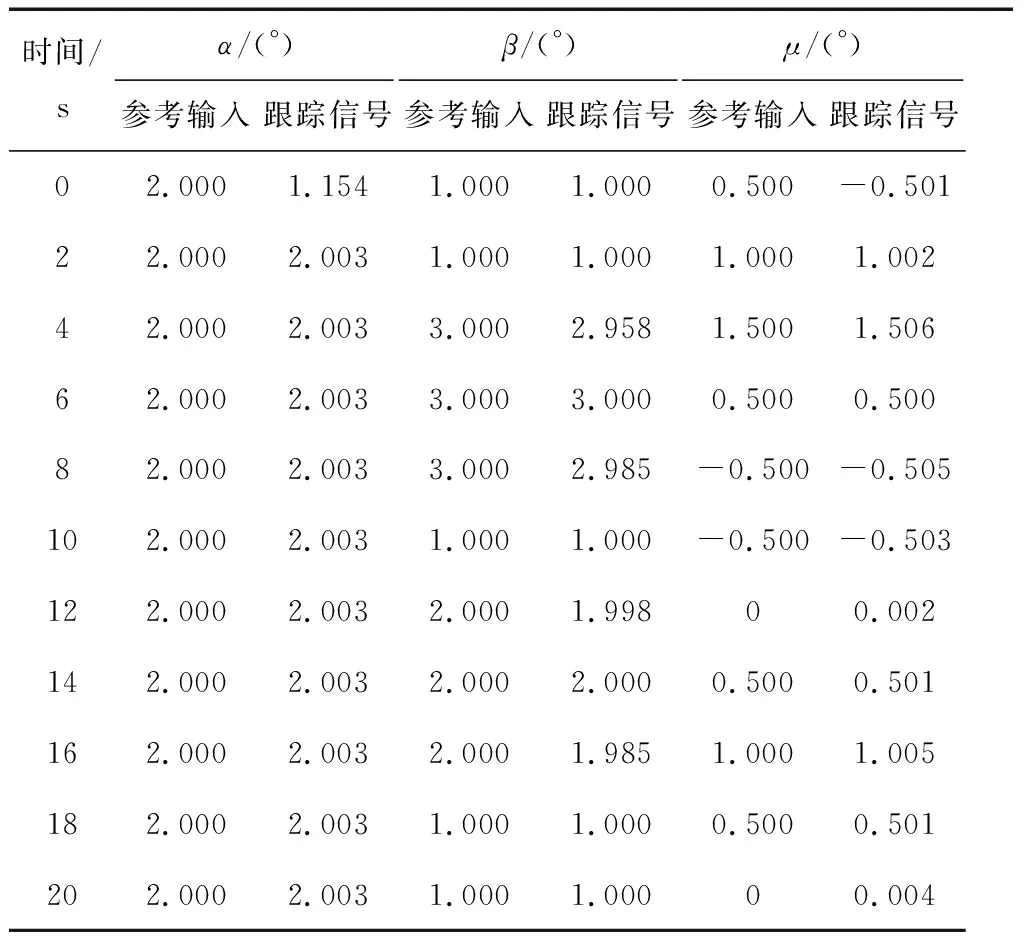
表1 姿态角跟踪效果测试结果

由表1可以知道，对于α姿态角，其参考输入为1条直线，参考输入的跟踪信号在初始的姿态角偏低，之后就迅速实现了切入信号的快速跟踪，并且跟踪的较为准确；对于β姿态角，其参考输入有规律性的2段波动，在波动处可以发现跟踪信号存在一些波动误差，在信号平稳处，则实现了切入信号的准确跟踪；对于μ姿态角，其参考输入是规律的波动形态，参考输入的跟踪信号在初始的姿态角偏低，之后就迅速实现了切入信号的快速跟踪，并且实现了较为准确的切入信号跟踪。综合而言，本文设计方法能够使时滞非线性切换系统实现较为准确的切入信号跟踪。

跟踪过程中的姿态角速率数据，如表2所示。

表2 姿态角速率跟踪效果测试结果

由表2可以知道，对于α姿态角对应的p速率，其参考输入呈现不规则波动状态，上下起伏比较大，整体跟踪有几处存在一定姿态角速率误差，剩余均较为准确；对于β姿态角对应的q速率，其参考输入上下起伏比较小，但存在反复上升、下降趋势，其整体跟踪姿态角速率误差较小，较为准确；对于μ姿态角对应的r速率，其参考输入表现出大幅上升与下降行为，其整体跟踪姿态角速率误差同样较小。综合跟踪过程中的姿态角速率测试结果，可以得出本文设计方法能够使时滞非线性切换系统实现较为准确的切入信号跟踪的结论。

2.4 切换时的复合干扰估计实验

利用本文设计方法对时滞非线性切换系统进行复合干扰估计，α姿态角、β姿态角和μ姿态角切换时的复合干扰估计实验结果如图2所示。

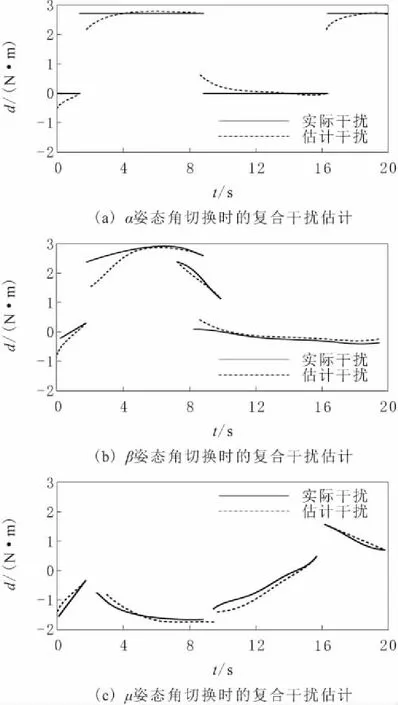
图2 切换时的复合干扰估计实验结果

由图2可以知道，μ姿态角对应的系统复合干扰估计最准确；β姿态角、α姿态角对应的系统复合干扰估计结果也较为准确。整体来说，本文设计方法表现出了很好的切换时的复合干扰估计性能，能够实现复合干扰的有效估计。

3 结束语

在研究时滞非线性切换系统滑模控制过程中，应用干扰观测器设计了一种非线性切换干扰观测器估计其不连续干扰，并设计了一种切换滑模控制器，实现了系统的滑模控制，取得了一定研究成果。