磁铁间距对双稳态压电悬臂梁俘能器输出特性的影响研究

韩飞燕,付 璇,卢竹青,豆卫涛

( 1.西安航空职业技术学院航空制造工程学院,陕西 西安 710089; 2.今创集团股份有限公司，江苏 常州 213012;3.西部超导材料科技股份有限公司,陕西 西安 710018)

0 引言

随着低功耗无线传感器件和微机电系统的迅速发展，利用环境中的振动能量进行微机电系统的自供电研究已经成为研究热点[1-2]，鉴于压电转换方式具有结构简单、能量密度高和易于微型化的特点，基于压电式的振动能量捕获装置越来越受到国内外研究学者的广泛关注[3-5]。

相比基于线性共振的能量捕获系统带宽狭窄的弊端而言，非线性共振具有较大的共振频宽。双稳态振动是典型的非线性振动，双稳态振子在振动过程中具有更大的振动幅值和工作频宽，便于产生更大的电量输出[6]。近年来，该方面研究受到了国内外学者的广泛关注，如王伟、曹军义等[7-8]根据人体腿部运动的振动特性，设计了一种适合于人体运动能量捕获的便携式双稳态压电悬臂梁俘能装置，建立了与腿部运动有关的时变双稳态势能函数，从理论和实验角度研究了含时变双稳态势能函数的压电能量捕获器的动力学特性和发电性能。张旭辉等[9]提出了双稳态磁力耦合式组合式压电悬臂梁俘能装置，采用哈密顿原理建立俘能系统的力学模型，从理论和实验角度研究了激励参数和结构参数对俘能系统动力学响应特性的影响规律。Paula等[10]以高斯白噪声为随机激励信号，研究了线性、非线性双稳态和非线性单稳态3种形式的悬臂梁压电发电系统的动力学行为，比较3种发电系统动力学行为及均方差电压受激励参数的影响规律。He等[11]研究了非线性环节在双稳态压电系统作用，分别从理论分析、数值仿真和实验的角度研究了谐波、白噪声和有色噪声激励下双稳态的动力学响应。Fu等[12]提出了旋转式双稳态振动能量捕获装置，建立了理论模型并进行了实验研究，有效改进了低频下系统的捕获性能。

压电振动俘能器发生双稳态运动的主要途径就是采用永磁铁产生非线性回复力，该力使压电振子的势能函数呈现双势阱状态，捕获频带变宽。但环境中的大量振动源的激励频率往往具有可变性，一旦环境激励频率偏离压电振子的工作频带时，其俘获效率将会很低，输出电能小,因此，需要能够及时调整压电振子的工作频率区间来适应环境激励源的变化，其中一种重要的方法就是调节非线性回复力的大小。磁铁间产生的非线性回复力与磁铁间距有重要关系。因此，研究磁铁间距对压电悬臂梁俘能器工作频宽和输出特性的影响，有助于提高俘能器的发电性能，有重要的工程应用价值。

1 双稳态压电悬臂梁俘能器建模

双稳态压电悬臂梁俘能器是由基座、悬臂梁、压电片、永磁铁和负载电路等组成，如图1所示。悬臂梁通过角铁固定在基座上，压电片紧密贴合在悬臂梁上，悬臂梁的末端固定1块磁铁1，在对面调节螺栓上安装另一块磁铁2，通过改变螺栓的伸入长度来调节两磁铁间距离，俘能器的支架通过螺栓与振动台实现固定。

图1 双稳态压电悬臂梁俘能器结构

采用集总参数模型，将图1的双稳态压电悬臂梁俘能器装置进行力学简化，得到俘能器的力学模型，如图2所示。其中me为悬臂梁和磁铁的等效质量，ce为系统等效阻尼，ke为悬臂梁的等效刚度，x为等效质量块的绝对位移，y为基座的绝对位移，则质量块的相对位移为z=x-y，Fm是磁铁间磁力，Fp是机电耦合力，表达式为

Fp=-kvV

(1)

V为电压；kv为机电耦合系数[13]，其大小为

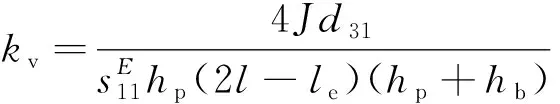
(2)

图2 双稳态压电悬臂梁俘能器力学模型

根据所建立的双稳态压电悬臂梁俘能器的力学模型，利用牛顿第二定律可以得到压电悬臂梁俘能系统的动力学方程为

(3)

因为

z=x-y

(4)

所以

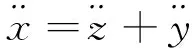
(5)

则式(3)可表示为

(6)

最后建立俘能器的机电耦合动力学方程为：

(7)

(8)

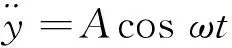
根据文献[13]中利用磁偶极子计算磁力的方法，可知两永磁铁之间的磁力为

(9)

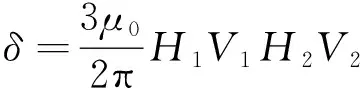
从式(9)不难发现，两永磁铁之间的磁力大小与磁铁间的距离有紧密联系。为了判断磁铁间距d的取值对系统运动形式的影响，将式(7)方程整理成一阶微分方程，计算其平衡点。

(10)

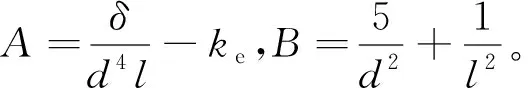
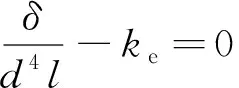
(11)

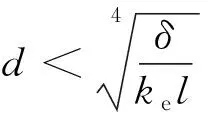
2 功率计算

系统输出功率的大小在很大程度上可以反映系统的供电能力强弱。输出功率可以通过俘能器输出电压的有效值进行计算。为了计算结果更具有说服力，采用系统在多个周期产生总功率的平均值作为评价发电能力的指标，所以双稳态压电悬臂梁俘能器平均输出功率P的表达式为

(12)

n为周期个数；R为负载电阻；T为输出电压的周期；ur为输出电压的有效值，表达式为

(13)

u为输出电压的峰值。

3 仿真分析

通过数值仿真研究磁铁间距对图1的双稳态压电悬臂梁俘能器捕获频率和发电效果的影响，系统的结构参数如表1～表3所示，负载电路等效电阻为R=2.5 kΩ。

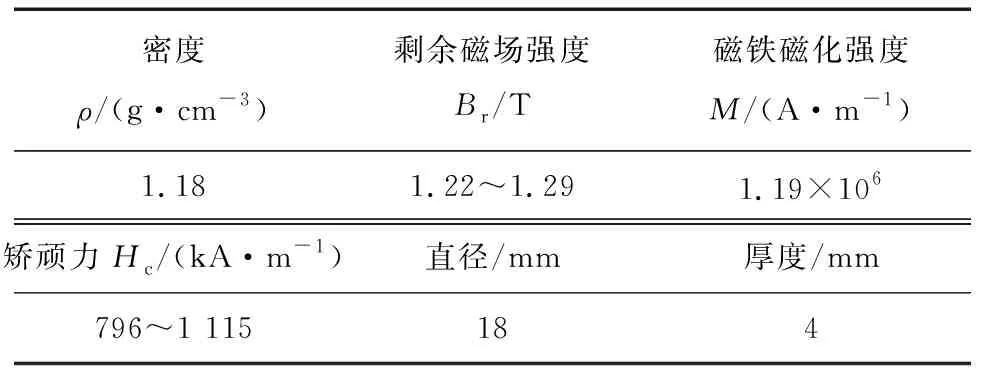
表1 钕铁硼磁铁参数

表2 磷青铜悬臂梁板参数

表3 PZT-5H压电片参数

由式(11)和表1～表3中数据计算得到磁铁间距的临界值为d=17.8 mm。当d>17.8 mm时，系统有1个稳定的零平衡点，只有1个势阱，这是因为两磁铁距离较远时，磁铁1与磁铁2之间的非线性斥力变得很小，系统处于线性状态。当d<17.8 mm时，系统有3个平衡点，2个势阱1个势垒，这是因为当磁铁间距适当时，磁铁间产生磁斥力给压电振子提供了足够的非线性回复力，振子在非线性回复力的作用下发生了双稳态运动。

现分别选取2种磁铁间距d=20.0 mm和d=16.0 mm来进行仿真比较分析。选取环境激励力类型为正弦激励，激励频率在3.00～80.00 Hz范围内。2种磁铁间距条件下系统的平均输出功率如图3和图4所示。为了确定俘能器在较大输出功率下的工作频率范围，本文借助半功率带宽法的思想，以最大发电功率的0.707倍画1条水平直线，该直线与功率曲线的2个交点即认为是俘能器有较大输出功率的起止频率。

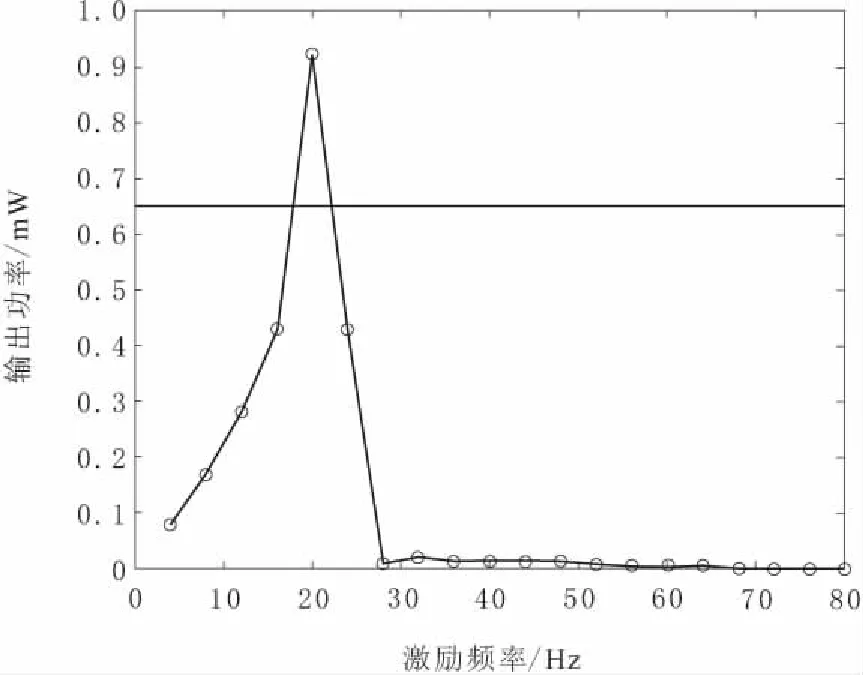
图3 d=20 mm时系统的输出功率

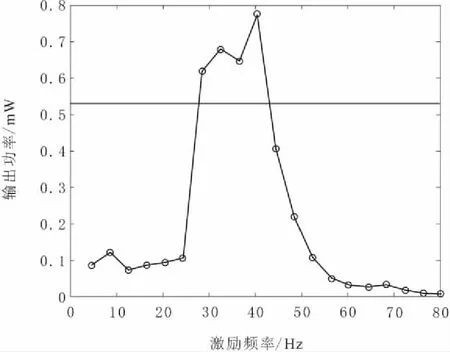
图4 d=16.0 mm时系统的输出功率

由图3和图4可知，当磁铁间距d=20.0 mm时，系统基本表现为线性，在20.00 Hz处出现共振，输出功率最大值为0.920 mW，出现较大输出功率的频带是17.78～22.22 Hz，工作频宽4.44 Hz。当磁铁间距d=16.0 mm时，系统发生了双稳态运动，此时系统发生较大输出功率的捕获频宽明显变大，俘能出现较大输出功率的频带范围27.45～42.55 Hz，工作频宽15.10 Hz，输出功率最大值为0.775 mW。虽然线性共振频率下的发电功率峰值略大于双稳态运动下，但是工作频宽明显小于双稳态系统，其他激励频率下的平均输出功率明显较低，俘能性能较差。可见磁铁间距的变化对俘能器捕获频宽和发电功率有重要的影响。

图5给出了正弦激励频率为30.00 Hz时，输出功率随着磁铁间距变化而变化的关系。可以看出，在激励频率为30.00 Hz时，俘能装置有较大功率输出的磁铁间距范围是12.5～17.5 mm，其中，在d=15.5 mm点出现最大输出功率。

图5 f=30.00 Hz时输出功率随磁铁间距的变化

图6给出了不同磁铁间距下，俘能器输出功率随着激励频率变化而变化的曲线。可以看出：激励频率不同时，磁铁间距的取值对系统输出功率有很大影响，俘能器的磁铁间距由20.0 mm逐渐调节至12.0 mm的过程中，俘能振子由线性运动转向双稳态运动，俘能器较大功率输出的工作频带逐渐向右偏移，频宽逐渐加大，但输出功率峰值略有减少。这说明，当激励源频率发生变化时，应该及时调整磁铁间距取值配置区间才能获得最好的发电效果，磁铁间距对系统的俘能频宽和俘能效果有关键的影响作用。

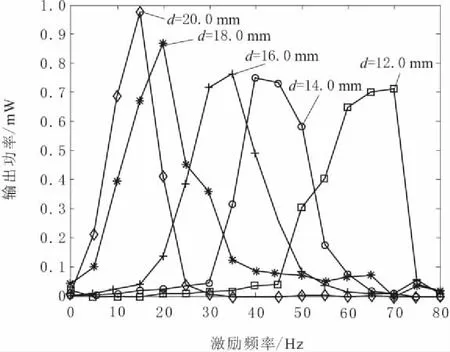
图6 输出功率与激励频率、磁铁间距的关系

4 实验

4.1 搭建实验测试系统

为了验证理论分析的正确性，进行实验研究。搭建了磁铁间距可调的压电悬臂梁俘能实验测试系统，如图7所示。压电悬臂梁俘能器固定在振动台上，一个磁铁固定在悬臂梁自由端，另一个磁铁固定在基座上，磁铁间距通过调节螺栓调节基座上的磁铁位置实现。俘能器悬臂梁尺寸和压电材料等的选取均与表1～表3一致。

图7 磁铁间距可调压电式俘能器实验系统

实验方法：通过计算机安装的振动台控制软件设置振动台激振的幅值和频率，振动台的固定加速度为24 m/s2，由数字信号发生器(YMC9200)产生相应的信号传递给线性功率放大器(LA-500)，经信号放大之后传递给振动台(VT300)，振动台带动压电式俘能器振动。由东华信号采集仪(YE6231)采集压电式俘能器输出的电压信号，并由激光振动测量仪(LDT-400)测量悬臂梁自由端的振动位移。实验中，通过改变激励频率和手动调节磁铁间距观察记录系统位移响应和电压数据，再进行数据处理获得系统响应的相图和发电功率。

4.2 实验结果

4.2.1 磁铁间距d=20.0 mm测量实验

通过调节旋钮，采用计量尺设定磁铁间距为d=20.0 mm进行压电悬臂梁振动俘能实验，改变系统激励源的激励频率测量对应的系统输出位移和输出电压，根据式(12)计算得到系统的输出平均功率并与理论仿真相比较，结果如图8所示。从图8中可以看到实验结果和仿真结果在趋势上基本一致，系统在磁铁间距为20.0 mm时表现为线性振动，只有在9.00～18.00 Hz频率范围内的输出功率较高。而当激励频率为30.00 Hz时，输出功率微乎其微，测量得到此刻的系统输出电压如图9所示。从图中10可以看到电路输出电压为5 mV，这是由于激励频率超出了系统俘获频率范围，系统处于小幅运动状态，振动能量不能被有效收集。

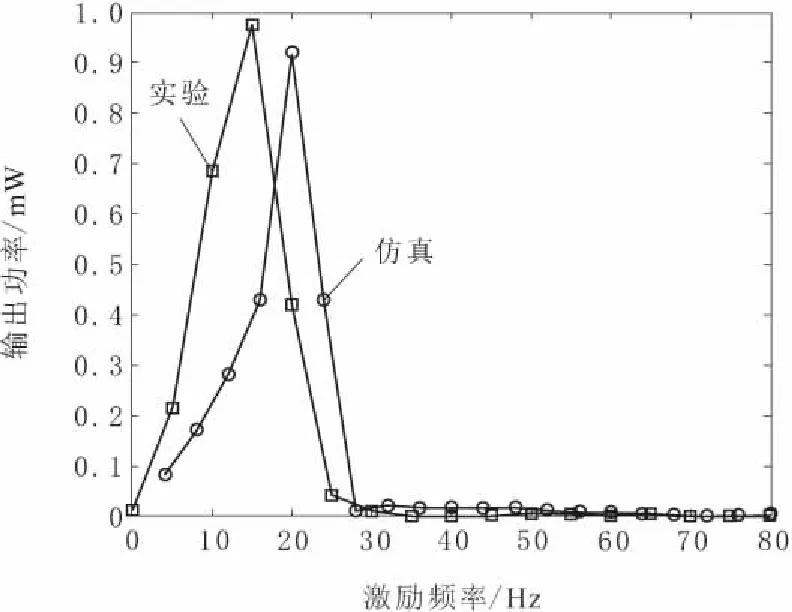
图8 输出功率随激励频率变化曲线

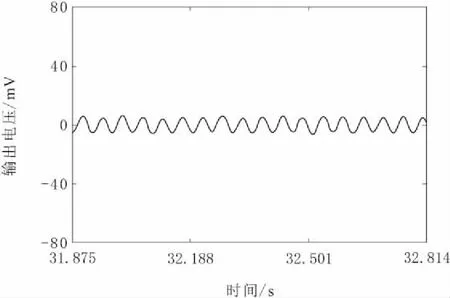
图9 f=30.00 Hz时的输出电压

4.2.2 磁铁间距d=16.0 mm测量实验

将磁铁间距调至16.0 mm，测量压电悬臂梁俘能器的位移响应和输出电压，计算获得系统的平均输出功率随着激励频率的变化曲线如图10所示。当激励频率为30.00 Hz时，压电悬臂梁的输出电压如图11所示。

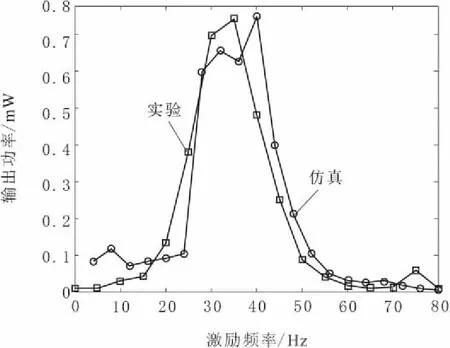
图10 输出功率随频率变化曲线

由图10可知，当磁铁间距d=16.0 mm时，系统在25.00～38.00 Hz频率范围内的输出功率较高，工作频宽变大，实验结果与仿真结果具有较好的一致性。当激励频率为30.00 Hz时，俘能器处于双稳态振动模式下，由图11可以得出系统在2个平衡点间产生了大幅周期运动，输出电压最大幅值达到了4 700 mV。

图11 f=30.00 Hz时的输出电压

4.2.3 磁铁间距与俘获频带关系测量实验

将磁铁间距从20.0 mm逐渐调节到16.0 mm，测量多组磁铁间距条件下，俘能器输出功率随激励频率变化的关系曲线如图12所示。从图12中可以看出，当环境激励频率变化时，需要及时调整磁铁间距使俘能器的工作频带适应环境激励变化才能获得较大输出功率。对比图6的仿真结果，可以看出实验结果和仿真分析具有较好的一致性。

图12 输出功率与磁铁间距、激励频率关系曲线

5 结束语

本文以双稳态压电悬臂梁能量捕获器为研究对象，针对环境激励源频率发生变化导致捕获效率降低的问题，进行了磁铁间距对双稳态压电悬臂梁俘能器输出特性的影响研究。建立了双稳态压电振子的动力学模型和磁力计算模型，理论推导出了系统发生双稳态运动的磁铁间距范围。数值仿真分析了环境激励源振动频率发生变化时磁铁间距变化对俘能器平均输出功率的影响规律。搭建了磁铁间距可调的压电悬臂梁振动能量捕获实验系统，测量了不同激励频率条件下，磁铁间距的变化与输出电压和功率的关系。对比实验结果与仿真分析，输出功率与磁铁间距变化规律较一致，证明了调节磁铁间距可以改变俘能器工作频带和频宽以适应环境激励源的变化，是提高双稳态压电悬臂梁俘能器发电性能的一种有效途径。本文在研究分析中采用了单个压电片，虽然能够获得系统的输出功率，但输出功率和电压值均较小，后续研究中应着重考虑提高系统的输出功率。