基于随机共振的机械传动系统机电耦合振动检测方法

王 琛

(西安职业技术学院机电工程学院，陕西 西安 710003)

0 引言

当前，机械设备的运行速度与精密化程度日渐提高，为保证各机械设备高效运转，需要对机械设备早期故障进行检查，及时发现设备异常情况，最大程度降低因为零部件故障带来的损失，以防止发生灾难性事故。对机械进行早期的故障检测，实质就是对机械运行状态进行信息识别，这些信息对于故障的预示与诊断是非常重要的。此次研究侧重于机械传动系统的研究，由于目前的电力电子设备结构日益复杂，工作强度日益增大，各模块间的交互与耦合关系日益密切，使得电力系统的动力学行为更加复杂。针对当前现状，一些学者开展了机械传动系统监测方法的研究，其中，秦大同等[1]研究了随机风速下风电传动系统机电耦合动态特性分析方法；刘利等[2]对多电机并联驱动-传动系统动力学建模及其固有振动特性进行分析。上述方法能够分析出传统系统的耦合效应，但是影响因素较多，导致振动检测效果不是很好。因此，本文提出基于随机共振的机械传动系统机电耦合振动检测方法。

1 基于随机共振的机械传动系统机电耦合振动检测方法

1.1 基于随机共振理论的信号噪声去除

利用随机共振理论中的郎之万方程来描述颗粒的运动，并将其他外力和引力的影响排除[3]，只考虑颗粒间的碰撞[4]。当随机力与变速无关时，噪声的强度随着附着力的改变而改变[5]，本文以信息理论为基础的测度方法对噪声进行测量，但由于非周期信号具有很大的频域范围，因此将其看作是一个信号的分度值。输入的二进制信号是相互独立的0和1序列[6]，则当前信道的误码率为

Pe=P(1)P(0|1)+P(0)P(1|0)

(1)

P(0|1)为输入为1时输出为0的概率；P(1|0)为输入为0时输出为1的概率。

信道容量为

C=r[Pelog2Pe+(1-Pe)log2(1-Pe)]

(2)

Pe为码率。

通过信道容量和误码率对信号好坏进行衡量，为振动检测提供基础。

1.2 机电耦合传动特性分析模型建立

在模型建立过程中，对涉及到的参数做基本假设[7]，将传动系统简化如图1所示。其中，O代表输入构件，X代表输出构件，A、B代表电力元件，a、b、c代表行星排构件。

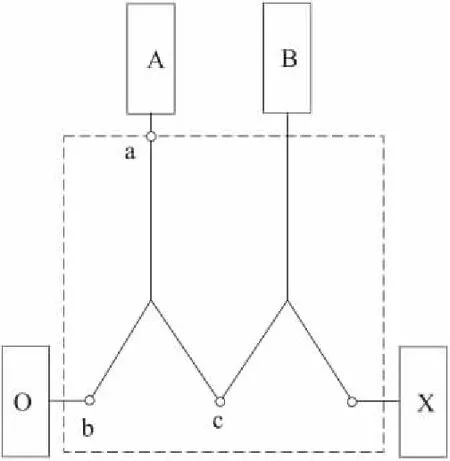
图1 传动系统

基于运动学特性[8]，推导整个传动系统的运动学传动比[9]，对耦合传动效率建模[10]，整个机电复合传动的效率η为

(3)

iB、iAB、iA、iBB分别为传动系统中特殊工作点对应的系数。机械传动系统运动过程中，每个机构都会存在动力损失，为此采用功率法分析计算，将传动效率表示为

η′=η-[(1-ηx1)β+(1-ηx2)β+…]

(4)

ηx1、ηx2分别为相对运动效率；β为相对功率系数。

1.3 机电耦合振动检测

机电耦合振动系统具有非线性特征，在模型建立完成的基础上，分析部分参数对系统振动的影响[11]。机电耦合分析过程如图2所示。

图2 机电耦合分析过程

机械传动系统运行过程中，机械负载往往是周期性变化的，周期性波动会引起转子电机的气隙磁场变化，使电流发生规律变化[12]。为简化分析，以传动系统非线性动力学为基础[13]，只考虑直流分量和基波部分，忽略各个物理量的高次谐波，传动系统机械负载表达式为

Tload(t)=T0+Tccosωt

(5)

ω为外界激励频率；t为时间尺度参数；Tc为负载转矩波动的幅值；T0为波动频率。当传动系统处于稳定状态时，机械转速为

(6)

τ为负载波动的恒定参数；J为机械转速；C为主共振解的幅频参数；d为激励频率失调系数。

在此基础上，分析参数变化对平衡点稳定性的影响，平衡点处的特征值能够体现出系统的局部稳定性，当扰动性较小时，将机电耦合振动方程转换为状态方程[14]，排除阻尼项和扰动项的影响，将系统转换为无扰动系统[15]。如果扰动项增加，会出现分岔现象，为此要对混沌阈值进行确定。在分岔分析时，无扰动系统方程为

(7)

κ为小参数；γ为相位；x为振幅。

通过上述计算，完成对机电耦合振动的定性与定量分析，完成传动系统机电耦合振动检测。

2 实验验证

2.1 实验目的

本次实验是在车辆上通过装车试运行进行的。在车速达到一定时，车辆会抖动并会发出低频噪声，随着车速增加，噪声频率和幅度也会增加。对此，采用所提出的随机共振检测方法与机电耦合动态特性分析方法(文献[1]方法)、固有振动特性分析方法(文献[2]方法)共同进行振动检测，共进行50次实验，取其平均值，获得实验数据，以此对比3种方法的检测效果。

2.2 实验系统组成

在实验中，配备4台交流电测功机、电池模拟分析仪。实验之前，将测功机连接，并与台架的驱动电机与驱动总成的发电机相连，实验平台如图3所示。

图3 实验平台

实验中，传动系统的主要参数值如表1所示。

表1 传动系统主要参数

在实验中，尽可能模拟真实的环境，采用电池模拟分析仪模拟电池供电方式，在实验过程中，关闭实验室的所有进出口，保证实验过程中没有其他噪声的影响。通过传感器采集数据，将采集到的数据存储到LMS Test Lab中，方便后续结果分析。

经过上述准备后，采用3种方法分析不同时间与频率下的转矩变化情况，结果如图4和图5所示。

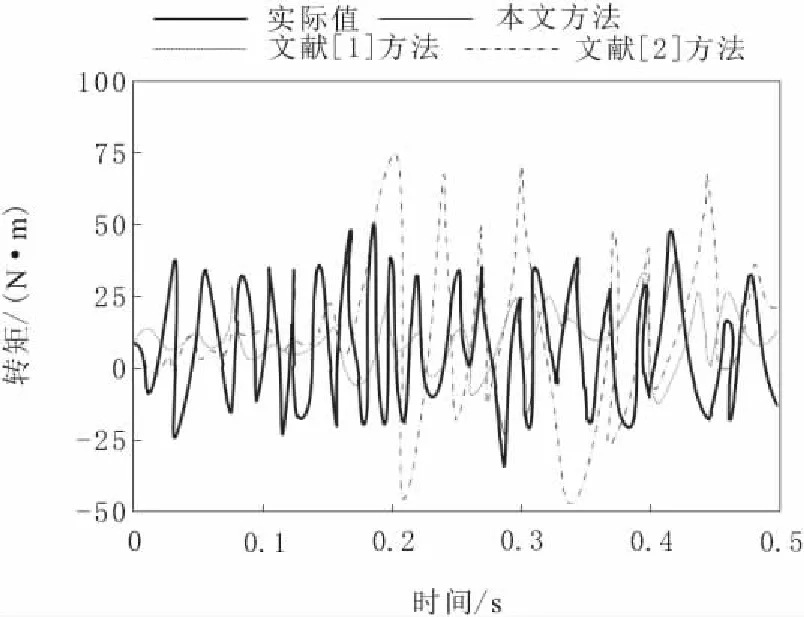
图4 不同时间下转矩变化情况

图5 不同频率下转矩变化情况

由图4和图5可以知道，本文方法在不同时间与不同频率下的转矩变化情况，与实际变化情况基本能够保持一致，比另外2种方法分析准确性高。3种方法不同时间与不同频率下电流变化情况如图6和图7所示。

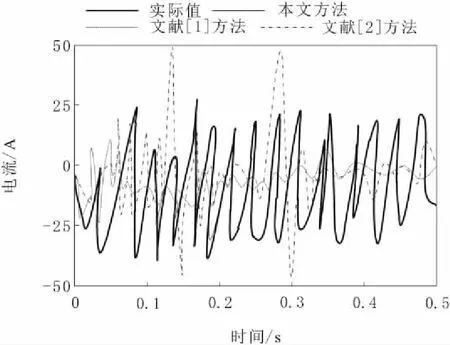
图6 不同时间下电流变化情况

由图6和图7可以知道，在不同时间和不同频率变化下，电流发生明显的波动情况，本文方法得到的结果与实际结果基本吻合，能够分析出电流变化情况。另外2种方法在检测中，虽能够检测出波动情况，但是与实际情况差距较大。

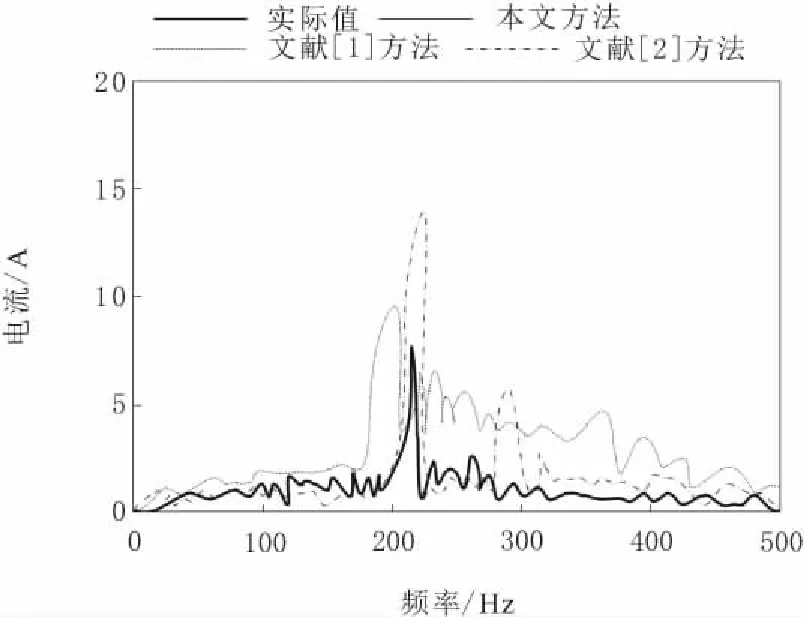
图7 不同频率下电流变化情况

接下来，采用3种方法检测中速轴外圈故障情况下的时频变化情况，如图8所示。

图8 中速轴外圈故障信号时频

由图8可以知道，在故障信号检测上，本文方法在有故障发生时，能够获得较为准确的信号时频图，比另外2种方法检测准确性高。

综上证明，本文方法能够较为准确地分析出传动系统振动情况。这是因为本文方法重点应用了随机共振理论，构建了动力学模型，较为准确地获取了振动规律。

3 结束语

本文提出基于随机共振的机械传动系统机电耦合振动检测方法，依据随机共振理论去除信号噪声，针对机电耦合传动特性建模，获得了振动的频率特征，计算机械转速并确定混沌阈值，实现了机械传动系统机电耦合振动检测。本文方法解决了以往机械传动系统机电耦合振动检测准确性低的问题，能够为后续机械传动系统机电耦合振动研究提供理论基础，由于客观条件有限，所提出的检测方法还需要进一步完善，在后续研究中，将着重研究机电系统中电磁场的瞬态性能，以进一步分析耦合振动规律，为机械传动系统控制提供参考。