机械传动在冲击载荷作用下的误差检测仿真
2022-08-22张庆利
刘 健,张庆利
(1. 北华航天工业学院机电工程学院,河北 廊坊 065000;2. 中国人民警察大学救援指挥学院,河北 廊坊 065000)
1 引言
在机械领域[1]中,人们普遍利用机械传动控制技术对机械传动进行控制,以此确保机械传动的控制精度。随着机械传动频率的提升,使人们对机械传动的要求愈加增多,若机械传动受到冲击载荷[2],那么在冲击载荷作用下机械传动会因此产生误差。为了避免这种问题的发生,需要对冲击载荷作用下机械传动误差进行检测。
杨坤[3]等人提出基于三维点云的机械加工精度自动检测方法,该方法依据配准误差点,将权值引入到机械残差迭代计算中,以此降低误差点对机械产生的影响,通过误差检验原理对机械加工精度评价方法进行设计,以此完成机械零件的识别和机械检测,该方法的设计效果不完善,存在机械传动信号漏报率多的问题。王海霞[4]等人提出机器人RV减速器传动误差的测量与分析方法,该方法首先建立了机械检测试验台,利用试验台对不同的传动误差进行检测,根据检测结果取得误差曲线图,通过试验台获取的数据,获取负载、转速与机器传动误差之间的关系,并对它们之间的关系进行分析,完成机器传动误差的检测与分析,该方法的分析结果不准确,存在机械传动信号覆盖率差的问题。曹科[5]等人提出精密齿轮传动误差检测试验台的设计方法,该方法根据动态齿轮传动误差理论及其技术,将高精密的传感器进行集成,并构建出传动误差检测试验台,依据各种实际情况对传动误差进行检测,该方法的集成效果不稳定,存在机械传动信号覆盖率低的问题。
为了解决上述方法中存在的问题,提出冲击载荷作用下机械传动误差检测方法。
2 机械的冲击载荷
一般情况下,机械会通过机械传动对金属施加压力,金属[6]会因此进行加工,在加工期间金属会随着压力的增大产生变化,这时的传动系统就会承受冲击载荷。
当机械对金属进行各种加工时,加工压力会随着行程增加或减少,其中个别区域也会具有一定压力。对机械进行剪切加工操作时,加工压力会产生剧烈的变化,这时对压力变化进行测量,并对n次拉格朗日插值多项式进行曲线拟合[7],拟合后的多项式用方程定义为

(1)
式中,经过n次插值后的加工压力由Ln(x)进行表示,而xi描述的是测量时间,yi描述的是测量压力,ωn+1描述的是第n+1次曲线拟合。
这时的压力曲线经曲线拟合和剪切加工后,就会产生机械冲击载荷。
2.1 冲击载荷作用下机械传动建模
以上述机械冲击载荷为基础,建立机械传动方程,如下所示。
1)位置方程
对机械的坐标系进行构建,设置A为原点坐标,AD之间的连线为x轴,而与x轴相垂直的就是y轴的正方向。通过封闭式测量法对机械传动位置方程进行构建,表示为:AB+BC=AE+ED+DC。这时,AB、BC、AE、ED、DC描述的是连线,即连线距离。那么这些连线之间的分量形式用方程定义为

(2)
式中,li描述的是机械i的杆长,其中i=1,2,3;θi标记为机械与x轴的夹角。
2)速度方程
对上述位置方程进行时间求导,从中取得冲击载荷作用下机械速度方程,方程(2)求导后定义如下

(3)
对式(3)进行整理,可得

(4)

3)加速度方程
通过冲击载荷作用下的机械速度方程求出机械加速度方程,因此需要对式(3)进行求导,定义如下

(5)
2.2 动力学建模
将拉格朗日法[8]与冲击载荷作用下的机械传动方程式相结合,共同构建出动力学模型。
由于冲击载荷作用下机械的拉格朗日函数可以对机械传动系统的动能和势能进行定义,而机械传动系统的动能与势能之差用L=K-P来表示,其中,L标记为机械传动系统,K标记为机械动能,P标记为机械势能。这时机械传动系统的拉格朗日方程定义如下

(6)
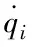
机械在进行平行运动时,它的刚体系统动能就是质心平移系统动能与转动系统动能的总和。因此可以计算出机械质心的速度,以此获取各个机械动能,质心速度通过方程表达式定义如下

(7)
利用广义坐标对机械上固定轴转动的构件和x轴上的滑块进行设置,即q1=θ1,q2=x。其中,q描述的是机械构件。这时的机械系统动能用方程表达式定义如下

(8)
式中,mi描述的是机械杆件质量,Ji描述的是机械杆件的转动惯量。
当机械在同一水平面时,它不能受到重力影响,因此机械重力势能表示为0。机械的总势能用方程定义为

(9)
式中,l0描述的是原点与固定点之间的距离,a描述的是机械弹簧的自由长度,k描述的是机械弹簧的刚度系数。
若机械系统的自由度为2,那么它的广义输入力就是机械杆件的输入转矩,将拉格朗日函数引入到式(8)与式(9)中,以此获取机械传动的动力学方程,表示如下

(10)
式中,τ描述的是机械弹性势能。
在冲击载荷作用下建立机械传动方程,将该方程与拉格朗日法相结合,完成对机械动力学模型的构建,并从中获取机械传动动力学表达式。
3 冲击载荷作用下机械传动误差检测方法
通过获取的机械传动动力学方程表达式,采用动态测量方法对其进行误差检测,从而实现冲击载荷作用下机械传动误差检测方法。
3.1 机械传动的反馈调节
采用动态测量方法对冲击载荷作用下的机械传动载荷及其强度进行计算,计算方程如下所示:

(11)
式中,I描述的是机械传动耦合特性,z描述的是强度。
与模糊参数识别方法相结合,对冲击载荷作用下机械传动进行反馈调节[9],那么机械传动反馈调节状态的方程表达式表示为

(12)
式中,Ci描述的是机械传动分布曲线的顶点,Wi描述的是权因子,P(u)描述的是机械传动载荷,Ri,k(u)描述的是机械传动强度,u描述的是自变量。
机械在最大动态响应条件下,得到的机械传动动态测量递推公式为

(13)
利用有限元模拟[10]获取机械传动冲击载荷的作用力矩,表示为

(14)
式中,P(u,v)描述的是作用力矩,Ni,k(u)、Nj,l(v)描述的是基参数。
通过上述分析,完成冲击负载作用下机械传动的反馈调节,依据力学参数评估结果对其进行动态测量,从而完成冲击载荷作用下机械传动误差检测。
3.2 机械传动误差检测
设置P′(u)为分割机械传动分布曲面的样条曲线,定义为

(15)
式中,u描述的是分布的时间函数,即u(ti)=ui,u(ti+1)=ui+1。这时对u实行动态力增益调节,取得

(16)
式中,ti描述的是插补时刻,ui描述的是稳态特征量,H.O.T描述的是不同冲击载荷下的高阶微量[11]。将不同冲击载荷下的H.O.T影响忽略,就可以取得机械传动参数增量Δui+1,表示为
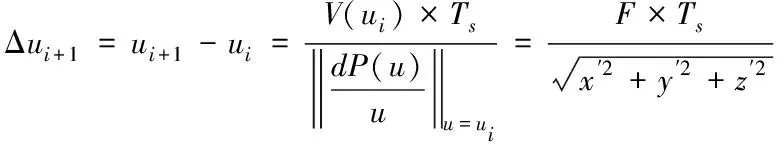
(17)
式中,Ts描述的是曲线插补周期,V描述的是速度。
通过模糊调节方法对冲击载荷作用下机械传动进行控制,控制结果为U0,与其相对应的动态测量值为:V1=V0+Acc0×T,其中,Acc0表示最大动态响应[12]。
对V1进行计算,以此完成机械传动动态测量,实现冲击载荷作用下机械传动误差检测。
4 实验与分析
为了验证冲击载荷作用下机械传动误差检测方法的整体有效性,需要对该方法进行实验对比测试。
采用冲击载荷作用下机械传动误差检测方法(方法1)、机器人RV减速器传动误差的测量与分析方法(方法2)和精密齿轮传动误差检测试验台的设计方法(方法3)进行实验测试对比。
1)为了验证机械传动误差检测方法的有效性,需要对机械传动误差进行检测前后对比测试,测试结果如图1所示。

图1 机械传动误差检测前后对比测试
分析图1中的数据发现,对冲击载荷作用下机械传动进行误差检测前,随着时间的增加,机械传动误差逐渐增加,可见检测前机械传动误差大,精准度低。对机械传动进行误差检测后,机械传动的误差急速下降,可见检测后的机械传动误差小,精准度高。
2)利用方法1、方法2和方法3分别对冲击载荷作用下的机械传动信号进行覆盖率对比测试。覆盖率越高,说明机械传动误差检测效果越好,覆盖率越低,说明机械传动误差检测效果越差,测试结果如图2所示。

图2 覆盖率测试
依据图2中的数据发现,当机械传动信号不断增加时,方法1的覆盖率始终保持最高,可见方法1的机械传动误差检测效果强。而方法3在测试期间,当机械传动信号为45到60时,它的覆盖率运动轨迹出现下降趋势,可见方法3的覆盖率效果差。方法2进行测试时,运动轨迹居于方法1与方法3之间,可见方法2的覆盖率要低于方法1,高于方法3。由此可见,方法3的覆盖率最低,检测效果最差。
综上所述,方法1的覆盖率最高,这是因为方法1对机械进行反馈调节,增强了机械传动信号覆盖率,以此提升了机械传动检测效果。
3)在上述实验的基础上,采用方法1、方法2和方法3分别对冲击载荷作用下机械传动信号漏报率进行对比测试,漏报率越多,说明机械传动误差检测准确率越低,漏报率越小,说明机械传动误差检测准确率越高,测试结果如表1所示。
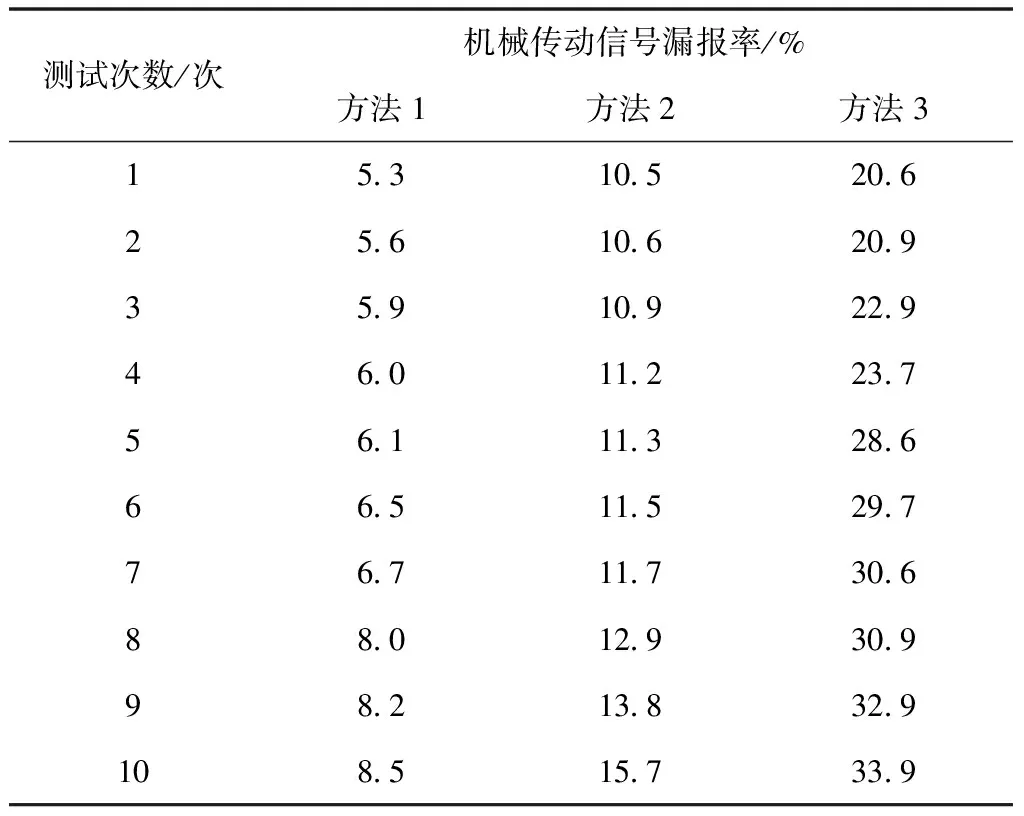
表1 三种方法的传动信号漏报率测试
根据表1中的数据发现,在测试期间,方法1的漏报率要低于方法2和方法3,而方法3的漏报率最高,可见方法1的机械传动误差检测准确率最高,而方法3的机械传动误差检测准确率最低。
5 结束语
现如今人们通过机械传动手段对机械进行控制,以此提升机械控制精度,但由于人们对机械传动的诸多需求,导致机械传动在冲击载荷作用下容易出现误差,为了避免这些误差带来的影响,提出机械传动误差检测方法。经调查发现,传统机械传动误差检测方法中存在机械传动信号覆盖率低和机械传动信号漏报率多的问题。
针对上述问题,提出冲击载荷作用下机械传动误差检测方法,该方法首先对机械的冲击载荷进行分析,以冲击载荷为基础构建机械传动方程,依据方程建立动力学模型,采用动态测量方法对该模型进行机械传动误差检测。该方法对冲击载荷作用下机械传动误差检测方法有着显著的帮助,为机械传动误差检测方法奠定了重要基础。
