问题驱动教学法的实践与思考——以苏科版八（下）“反比例函数”复习课教学为例

■季承洁

问题驱动教学法是一种基于问题的教学方法。该教学方法以学生为主体，以问题为学习起点及核心，规划教学内容，让学生围绕问题寻求解决方案。教师在此过程中是问题的提出者、课程的设计者以及结果的评估者。问题驱动教学法能够提高学生学习的主动性以及在教学过程中的参与程度，激发学生的求知欲，活跃学生的数学思维。而单元复习课是在整章内容学完之后安排的，目的是帮助学生回顾已学内容、形成知识网络，提高学生探究能力以及综合运用知识的能力。在新授课时，学生获得的知识相对松散，为了提高学生对知识的整体认知，笔者尝试运用问题驱动教学法，唤醒学生对知识的记忆，并在此过程中建构“反比例函数”的知识网络。

一、教学过程

1.创设情境，生成新知。

师：请一名同学描述自己在教室的位置，用几何画板画出一个点，对于平面内一点，你如何描述它的位置？

【设计意图】笔者从生活中的数学入手，激发学生学习兴趣。

2.师生合作，建构框架。

生1：建立平面直角坐标系，在平面直角坐标系中表示出这个点的坐标。

师：已知一个点的坐标可以确定什么函数？生2：正比例函数或反比例函数。

师：已知反比例函数图像经过点A（4，2），？请同学们自行提出问题并解答。生3：求这个反比例函数表达式。

师：你是运用什么知识解决这个问题的？

生3：用反比例函数的定义以及待定系数法求函数表达式。

师：谁能针对对称性提出一个问题？

生4：求点A关于原点的对称点。

师：利用反比例函数中k的几何意义能不能再提出问题？

生5：在反比例函数图像的第一象限的分支上另外取一点B，过点B分别作x轴、y轴的垂线，过点A分别作x轴、y轴的垂线，试比较S1、S2的大小（如图1）。

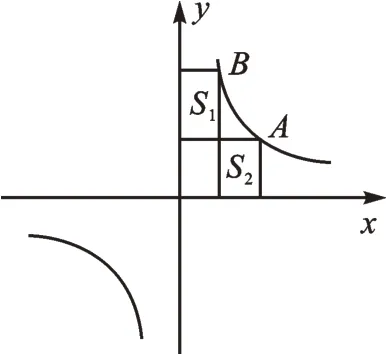
图1

生6：在反比例函数图像上任取两点（x1，y1）、（x2，y2），当x1＜x2时，y1与y2有什么样的大小关系？

师：解决问题时，你运用了什么知识？

……

【设计意图】复习的目的就是帮助学生既理解基础知识，也形成知识网络。笔者设计了一个开放性问题，让学生自主提问并解答，充分发挥学生的主体作用。学生提出了多个问题并加以解决，参与活动的积极性较高，教学效果自然很好。

3.提升能力，回归题目。

师：下面我们看一道例题。

例为了做好校园疫情防控工作，学校工作人员每天早上对全校教室进行药物喷洒消毒，药物在一间教室内空气中的含药量y（毫克）与时间x（分）的函数关系如图2所示，进行药物喷洒时y与x成正比例函数关系，药物喷洒完成后y与x成反比例函数关系。根据图像提供的信息，解答下列问题：（1）求y与x之间的函数表达式及自变量的取值范围；（2）根据要求，只有当空气中每立方米的含药量不低于4毫克时，对预防才有作用，且至少持续作用15分钟以上，才能完全消灭病毒，请问这次消毒是否彻底？

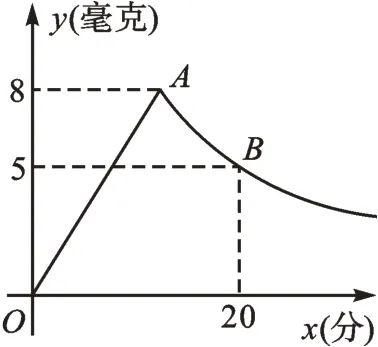
图2

【设计意图】基础知识的复习可以为学生综合运用所学知识解决问题打下基础。

4.回顾梳理，巩固提升。

师：今后我们会用怎样的眼光看反比例函数？

【设计意图】帮助学生站在更高视角重新审视反比例函数的知识点，找到反比例函数与其他知识点之间的联系，建立更加完整的知识网络图。

二、教学反思

本节课，笔者以生活中的问题为背景创设教学情境，以课堂产生的问题和预设的问题为载体，与学生共同合作，引导学生自主探究学习，培养学生解决问题的能力，帮助学生建构整章知识网络，理解分析类比、归纳的思想方法，体会数形结合的数学思想，从而提高学生数学核心素养。

专家点评

本节课通过问题驱动教学法，帮助学生重新回顾知识点，提高学生的整体认知，具体表现在以下四个方面：

基于整体化的设计。复习课不再是知识的重复，季老师对本节课的设计有一个整体化的思考，不拘泥于本章的知识点，从一个点开始，让学生思考能确定什么函数。学生不仅能确定反比例函数，还能确定正比例函数；不仅复习了反比例函数图像及性质，还复习了用待定系数法确定函数表达式。

基于问题解决的设计。课程目标以学生发展为本，以核心素养为导向，进一步强调使学生获得数学基础知识、基本技能、基本思想和基本活动经验，发展学生运用数学知识与方法发现问题、提出问题、分析问题和解决问题的能力。季老师引导学生从反比例函数和正比例函数关系入手，从不同视角发现问题、提出问题，引导学生用不同方法去分析问题、解决问题，过程中还对学生的能力表现给予及时恰当的评价。

突出重点知识讲解。本节课问题设计突出研究函数的通性通法：解析法、表格法、图像法。结合图像重点复习了反比例函数图像的对称性、k值的几何意义及应用。探究过程以学生为主体，反比例函数的应用从数学应用到生活应用，教师引导自然，学生问题生成丰富，体现出真实情境下的深度学习。

突出思想方法渗透。数学问题研究的一般方法是先研究对象再研究关系，正比例函数和反比例函数是已经学过的两种重要函数，季老师以图像为抓手，让学生借助图像直观比较反比例函数与一次函数的大小，感受到数形结合思想的重要性，明白分类的必要性和重要性。