从知识的生长点与延伸点浅谈简约教学

广东省深圳市龙岗区宝龙学校 钟泳诗

《义务教育数学课程标准（2022年版）》指出，在教学中要重视对教学内容的整体分析，帮助学生建立能体现数学学科本质、对未来学习有支撑意义的结构化的数学知识体系。一方面了解数学知识的产生与来源、结构与关联、价值与意义，了解课程内容和教学内容的安排意图；另一方面强化对数学本质的理解，关注数学概念的现实背景，引导学生从数学概念、原理及法则之间的联系出发，建立起有意义的知识结构。这就要求教师注重研究知识的“生长点”与“延伸点”，把每堂课的知识置于整体知识的体系中，注重知识的结构和体系，处理好局部知识与整体知识的关系，引导学生感受数学的整体性。当学生不是在学习一个单一的知识点，而是在建构一座数学的知识大厦时，学生就不需要靠记忆去完成每节课的学习，而是可以更开放、发散地开展数学探索，从而减轻学习压力。教师思考“知识的生长点”，根据学生知识的最近发展区设计课堂的导入方式，能帮助学生更简单、直接地进入新知的探索中，达到简约探索新知的目的；教师思考“知识的延伸点”，根据新知的内涵与外延，设计变式题或追问的“问题串”，可以帮助学生更快捷、根本地解决知识“是什么” “为什么” “怎么用”的三大问题，达到简约获取新知的目的。

一、挖掘最近发展区，简化知识生长过程

我们必须了解学生的最近发展区，只有了解了学生的最近发展区，我们的导入才是直接的、简单的。我们要给学生做好知识的承接工作，就要思考要接什么：一是接学生原有的学习状态、学习基础与学习习惯；二是接学生的真实生活与经验；三是接新旧知识与方法，架设新旧知识、新旧方法之间的桥梁。

（一）旧知“接”新知

当新知的生长点是旧知的时候，我们要追溯学生已有的认知结构，帮助学生建立新旧知识之间的联系，体现知识的一致性与整体性。例如，在学习加减计算时，如果脱离新旧知识联系，单纯讲授整数、小数、分数加减法的算法，那对学生来说，三套算法就是三倍的学习压力。但是，只要厘清知识的生长点与延伸点，就能发现：小数和分数的加减法算理与整数的一致，都源于“加减计算时要统一计算单位”，结果都是为了“用统一的单位描述和差关系”。如此，学生在学习小数和分数加减法的时候就会豁然开朗，尤其在分数加减法中，学生就能明白分数加减法算理与整数是同源的，通分只是让不同单位的分数统一单位的方法和手段，加减法计算的前提还是要统一计算单位。

对于从旧知过渡形成的新知，教师可以如何帮助学生做好知识的承接工作呢？教师需要利用类比、转化等数学思想方法，帮助学生厘清新旧知识间的联系，帮助学生找到最简约、最直指根本的探索路径，从旧知中迁移，获得新知。例如：在教学“小数的初步认识（一）”时，教师要厘清在有分数的基础上，为什么还要学习小数？小数和分数的联系又是什么？它们的联系是小数是分母为10、100、1000……的特殊分数，小数是满足十进制的特殊分数。明白这个联系后，就能发现小数的意义的生长点：分母是10、100、1000……的特殊分数意义，则分数的意义是小数意义的最近发展区。为此，我们做了以下学习前的知识准备：

写出下面线段表示的分数：

三幅线段图中分数的分母从普通分母到分母是10的特殊分母过渡，为学生后面理解小数是分母为10、100、1000……的特殊分数做铺垫。这个导入，是为了让学生通过回顾分数的意义，观察分数中分母的区别，为下文继续延伸小数的意义、小数与分数之间的关系提供了一条可触碰、可猜想的便捷且指向学习目标的路径。

在以上的例子中，知识的生长点是“旧知”。教师根据学生认知的最近发展区顺势设计符合学生认知规律的导入方式，从旧知到新知，让学生体会知识的整体性与一致性，体会类比与转化等数学思想方法。简单、根本、开放的承接方式，让所有学生都“有话可说”，提高了学生的自我效能感。

（二）生活“接”新知

当新知的生长点是生活规律的时候，我们要挖掘生活现象，帮助学生发现、总结生活规律，体会数学源于生活又应用于生活的学科特点。例如，在理解“两点之间线段最短”这一公理时，如果脱离生活实际，单纯构造模型进行讲授，学生就比较难理解。但是，先挖掘这一公理的生长点——生活中的“最短路线”问题，再抽象、总结这一生活规律，学生便能更好地理解这一公理。

对于从生活中来的新知，教师如何帮助学生做好知识的承接工作呢？我们需要利用分类、抽象、归纳的数学思想方法把生活实例根据特征进行归纳，帮助学生体会新知和生活的联系，从生活中抽象归纳新知模型。例如：在教学“线的认识”时，教师提供多种生活中的“线”让学生进行分类，让学生把不同类型的线用图示的形式进行抽象，归纳不同类型的线的特征，从而认识“线段、射线与直线”。我们为学生提供了如下的生活背景作为感知储备：

观察下图的线，进行分类并说明分类原因。

①桥上钢筋

②车灯光线

③竖琴琴弦

④太阳光线

⑤海平面与天际交线

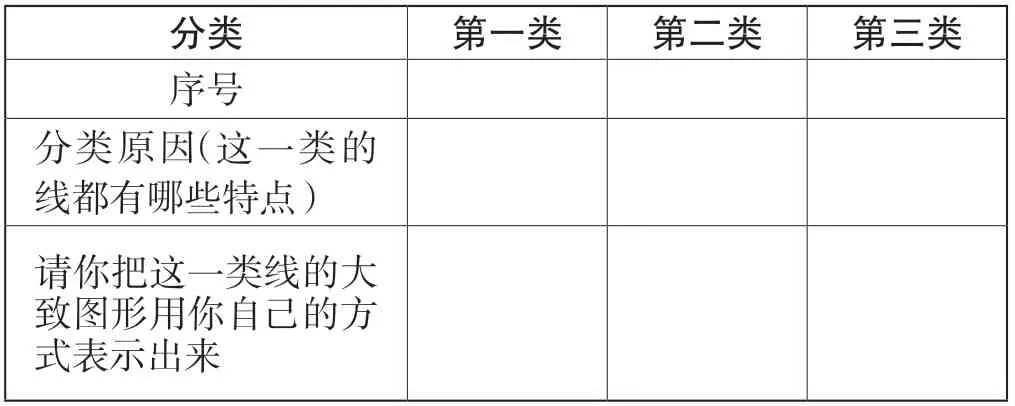
分类 第一类 第二类 第三类序号分类原因（这一类的线都有哪些特点）请你把这一类线的大致图形用你自己的方式表示出来

这样的导入，挖掘了学生日常能接触到的生活现象，是学生的最近发展区。教师让学生直观感受并引导学生理性抽象出不同现象的异同点。这样简单的生活例子，对于新知的探索来说，学生不仅有浓厚的探究兴趣，而且有可尝试、能思考的方法路径。

二、思考知识内涵与外延，简单达成知识延伸

了解了知识的来源，我们就要研究如何进行新知的延伸。如何让大部分学生轻松、简单地掌握知识？我们认为，首先要弄清楚知识的“三个点”，即矛盾点、模糊点、跃迁点。矛盾点就是本节课中新知与旧知之间的冲突或者新知与新知之间的冲突。矛盾点的突破，需要教师设计新旧知识之间的冲突，引发学生讨论。模糊点就是新知中、概念里或者方法技巧上的一些容易混淆、出错的地方。模糊点的整理，需要教师通过追问或者提供简单的题目来帮助学生进行梳理。跃迁点就是可以让学生举一反三的知识的本质。跃迁点的感受，需要教师通过变式，让学生体会知识的运用方法。

在传统的课堂中，教师习惯于设计很多自己认为“环环相扣”的环节，一步一步指引着学生达成教学目标，再加以练习。上课前总觉得内容很多，担心讲不完，一直想着如何让自己的语速更快，让学生听得更多；想着如何能让学生顺利地从这一个环节过渡到下一个环节；还要想非常多的预设，生怕学生会卡在某个环节上过不去。这些设计，确实是环环相扣的串联模式。但是，只要学生在一个环节上卡住，那么接下来的环节基本是不可能跳过的。这样的过程，无疑使学生形成两极分化。这种课堂对学生来说是一种压力。

在我们追求的简约课堂中，教师只要做好引领就可以了。“引”，一是引领学生的学习方向；二是引发学生的学习兴趣与学习需求；三是引起多维的对话。我们以“假设—验证”作为矛盾点的激发手段，以小组讨论和展示作为矛盾点的碰撞载体；以教师的追问和总结作为模糊点的厘清方法；以归纳特征和变式练习作为跃迁点的感悟途径。总的来说，新知中，“三点”的梳理，是通过追问问题或者数学题目让学生最直接地感受知识的本质。学生能最大限度地在问题中厘清知识的“样子”，而不是教师一直在讲知识长什么样子。这样的课堂是简单愉悦的。

具体从下面的例子中看看如何做到简约地“引”。在“合格率”的学习中，教师设计了以下环节：下表是质检工人对甲、乙两个牌子罐头的抽查情况。你认为哪种罐头质量更好？

抽查箱数 合格箱数甲牌 50 43乙牌 50 48抽查箱数 合格箱数甲牌 50 43乙牌 64 43抽查箱数 合格箱数甲牌 50 43乙牌 64 48

通过抽查箱数一样而合格箱数不一样、合格箱数一样而抽查箱数不一样的产品，进行同分母或同分子大小比较，降低学习门槛，学生能够很容易总结出比较方法：要比较质量优劣，得先统一其中一项变量。这样低门槛的引入给学生指明了探讨方向。接下来，进行抽查箱数与合格箱数都不一样的优劣情况对比，从单一变量到多重变量的过渡，教师挖掘矛盾点使学生产生思维碰撞，引发学生的学习兴趣与学习需求，学生很容易得出结论。

接下来，我们并没有局限于讨论任务求“合格率”或者用百分数来解决问题，而是改为开放的思路。学生可以用小数、分数、百分数等多种表示方法验证自己的猜想，用任意的方法判断产品优劣，引发学生的多维对话。

最后，教师引导学生进行对比，发现用百分数形式更有利于进行大小比较。学习并感受了特殊百分数“合格率”后，教师总结“合格率的样子”——“合格数量占产品总数量的百分之几”，进而给出题目，延伸出“成活率” “发芽率” “出勤率”“出生率”等特殊百分数的意义与求解方法。

请同学们类比“罐头合格率”，判断正误：

1.一批产品的合格率是200%。（ ）

2.同学们植树，有99棵成活，1棵死亡，成活率是99%。 （ ）

3.某校六年级共有99个学生，今天全部到校上课，该校六年级今天的出勤率为99%。 （ ）

4.王师傅用400千克的油菜籽榨出菜籽油168千克，这批油菜籽的出油率是42%。 （ ）

这几道题目的设计抓住“合格率”的本质进行延伸，让学生深刻感受部分与整体之间的关系、感受“合格率”的求解方法。

整节课由教师提供问题背景并引领学生思考，学生自行猜想并验证，以开放的思路获取了最简单本质的知识与方法。教师在教学过程中只是作为引领者，总结了使用百分数的便利。最后通过变式题达到“一通百通”，学生在学习时学到的不只是一个“合格率”，而是整体与部分的一种新的表示方法。这种新的表示方法不是孤立的新知识，而是相对于之前的小数、分数的表示方法而言的一种更加便利直观的表示形式。

教师只有深刻分析每节课的“生长点”和“延伸点”，课堂才能真正地做到“简约”。思考学生的最近发展区，有利于学生更直接地进行新知的探索，给学生提供一条切实可行的路径。这样生长起来的知识才不会是孤立的，而是系统的，系统的知识对学生来说才是简单的。思考知识的内涵与外延，设计问题串追问知识的本质，可以帮助学生厘清知识，进而帮助学生了解知识“是什么” “怎么用”。只有让学生明白知识的“样子”与“应用途径”的课堂才是高效的，对学生来说才是轻松的、有收获的。