高速列车车体小部件模态修正及试验验证
2022-10-31张海进赵艳菊郭建强帅仁忠
张海进,赵艳菊,郭建强,帅仁忠
(中车青岛四方机车车辆股份有限公司,山东 青岛 266111)
目前高速列车车体大多采用轻量化的铝合金材料,使得车体的固有频率降低。列车在高速运行过程中车体不仅受到来自轮轨的宽频振动激励,还受到较大的气动载荷压力,使车体产生了较大的振动能量[1-2]。因此研究车体的振动特性对提高乘客的乘坐舒适性有着重要的意义,也为设计与优化高速列车车体提供理论基础[3-4]。有限元分析是高速列车车体设计中的重要方法,但由于初始的简化假设、边界模拟的差异以及非结构构件等因素的影响,使得建立的有限元模型总与实际模型存在差异,造成计算值和试验测量值存在一定偏差。结构有限元模型的修正是以试验模态的结果参数为目标,在一定范围内对有限元模型参数(如几何参数、约束边界、材料属性等)进行修正,使结构的动力特性的理论值更趋于实测值[5-6]。高速列车特殊的双层薄壁型材结构导致有限元网格多,计算量大,需要在保证精度的前提下提高计算效率。张德文 等对模型修正的理论与方法进行了详细的阐述[7];费庆国 等通过数值算例对以模态参数为特征量的有限元模型修正技术进行了深入探讨[8];Kenigsbuch et al.选取模态频率和模态振型作为特征量对6自由度的弹簧质量体系进行了修正[9];Mottershead和Friswell在利用模态参数进行模型修正方面作了大量的研究,分别研究了基于模态频率、模态频率+模态振型、模态频率+模态置信度的修正方法[10-11]。
初始有限元建模是有限元模型修正的出发点,该模型提供了修正的初值,应以尽可能小的误差反映结构的真实特性。良好的初始有限元模型对于修正的速度、精度乃至修正的成败至关重要。初始有限元模型的误差分为结构误差、参数误差和阶次误差三类[12]。结构误差可以通过寻找合理的数学模型解决,阶次误差也可以通过有限元网格离散疏密得到最大限度的缩小。因而有限元模型修正的焦点是怎样缩小有限元模型和实际结构之间的参数误差[13]。
本文以高速列车车体型材为对象,对其进行有限元建模、模态计算,同时对其进行试验模态分析,将有限元计算结果和试验结果进行对比,利用基于灵敏度分析的有限元模型修正方法[14-15],对型材的有限元模型进行修正并进行模态计算。
1 基于灵敏度分析的有限元模型修正
基于灵敏度分析的参数型模型修正方法的实现是一个迭代的过程,主要包括以下步骤:初始有限元建模、有限元分析、试验建模及分析、试验振型扩充/有限元模型缩聚、相关分析、误差定位/参数选择、灵敏度及残差分析、修正量求解、收敛判断、质量检验等。已知结构的有限元模型共有n个设计参数,其中前m个为待修正的参数,则设计参数p可以表示为:
(1)
结构的总体刚度阵K和质量阵M可以用设计参数p的函数表达:
(2)
则对应的特征量可以表示为设计参数的函数:
f=F(K,M)=F(fK(p),fM(p))=fp(p)
(3)
式(3)中,f可以是任意的特征量,如模态频率、模态振型等,或者是它们之间的组合。模型修正问题转化为如下的优化问题:
(4)
式中:fe,fp(p)——分别为结构动态特性的试验值与分析值;
该公司的科学家通过“关闭”大豆中反式脂肪酸基因研发出这一款转基因大豆。与传统的大豆相比,这种大豆榨取的豆油含有更多“健康”的脂肪酸,而导致人体胆固醇增多的脂肪酸更少。
R(p)——残差项;
VLB,VUB——分别为结构设计参数变化的上下限;
Wf——结构各个特征量之间的加权矩阵。
通常情况下,fp(p)为设计参数的非线性函数。为将非线性问题转化为线性问题,在初始设计点将fp(p)展开成待修正参数的一阶泰勒表达式:
fp(p)=fp(p0)+SΔp
(5)
其中:
(6)
式中:S——特征量对设计参数的灵敏度矩阵;
p0——设计参数初始值;
Δp——设计参数的误差,Δp=p-p0。
WfSΔp=Wf(fe-fp(p0))
(7)
式(7)就是常见的模型修正方程,且是一个迭代优化的过程。
2 型材有限元模态计算和试验模态测试
2.1 型材有限元模型仿真计算
本文中使用1.5 m×1.2 m的高速列车车体用铝型材进行建模仿真计算及试验模态测试,型材实际质量为35 kg,材料密度取2 800 kg/m3,确保模型总质量为35.04 kg。型材及几何模型如图1所示。为了比较网格尺寸对模态分析结果的影响,精细模型的网格为30×20,粗糙模型网格为20×10(图2)。

图1 型材及几何模型

图2 2种有限元模型(FEM)
对2种有限元模型进行模态计算,得到的前14阶模态频率见表1。从表1中可以看出,随着阶次频率的增加,有限元精细模型和粗糙模型的计算结果偏差越来越大。图3~图6为2种有限元模型计算的前4阶模态振型。
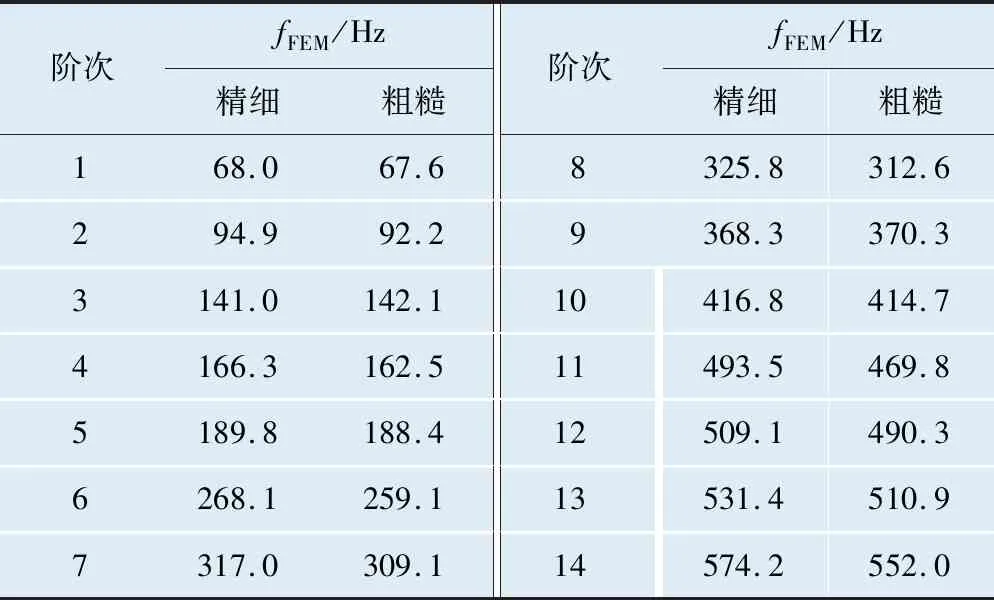
表1 FEM精细模型和粗糙模型模态计算结果
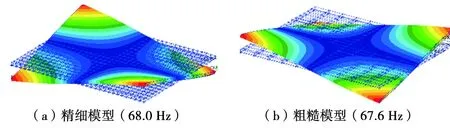
图3 1阶扭转振型
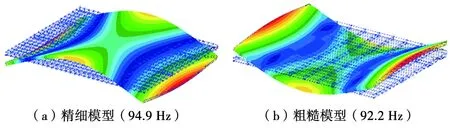
图4 1阶纵弯振型(1.5 m方向)
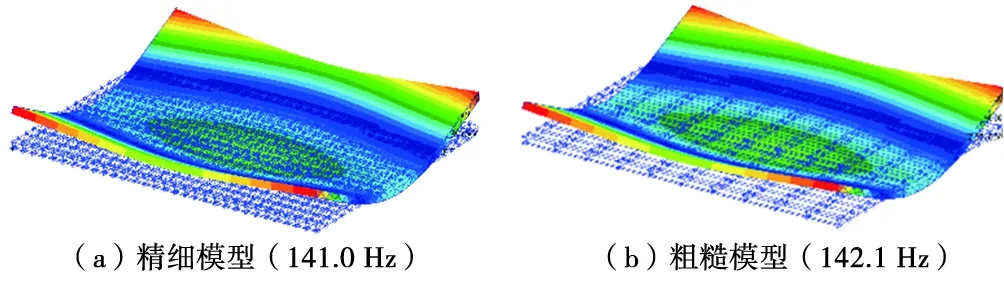
图 5 1阶横弯振型(1 m方向)
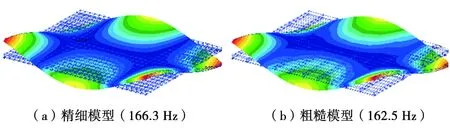
图 6 2阶扭转振型
2.2 试验模态测试
试验模态中横向和纵向各布置11个测点,整个型材共布置11×11个测点,采用移动锤击法进行模态试验测试,频率测试结果见表2,前4阶模态振型如图7所示。

表2 试验模态(EMA)测试结果
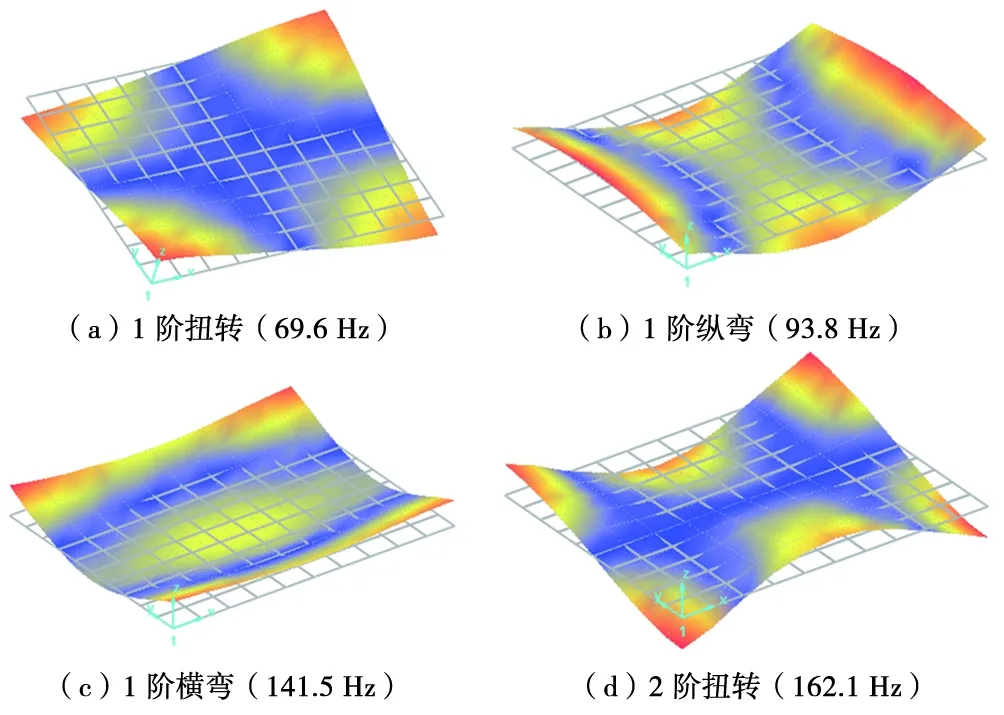
图7 试验模态振型
2.3 相关性分析
根据有限元模型修正的定义可以看出,无论哪一种修正方法,都是某种类型的有限元分析结果与试验结果根据某种准则进行比较的结果,因此,模型修正技术首要考虑的就是理论-试验模型的相关性分析。相关性分析的作用是为了确定计算分析结果和试验测试结果的对应关系和误差准则,以便进行模态匹配。模态匹配的方式除了对振型进行比较、观察外,还可以利用数值的手段,例如模态比例因子(Modal Scale Factor,MSF)和模态置信度(Modal Assurance Criterion,MAC)。
模态置信度,也称为振型相关系数,是一个介于0~1之间的标量,如2个振型向量的MAC值为1,则说明2个振型向量代表的是同一阶模态,为0则代表不同模态[16]。实际运用时,MAC是一个矩阵,好的相关性要求MAC矩阵的对角元>70%,非对角元<10%。对2种有限元模型和试验模态进行振型相关性分析,选择z向平动自由度进行MAC计算,结果见表3,前14阶MAC值三维柱状图如图8所示。
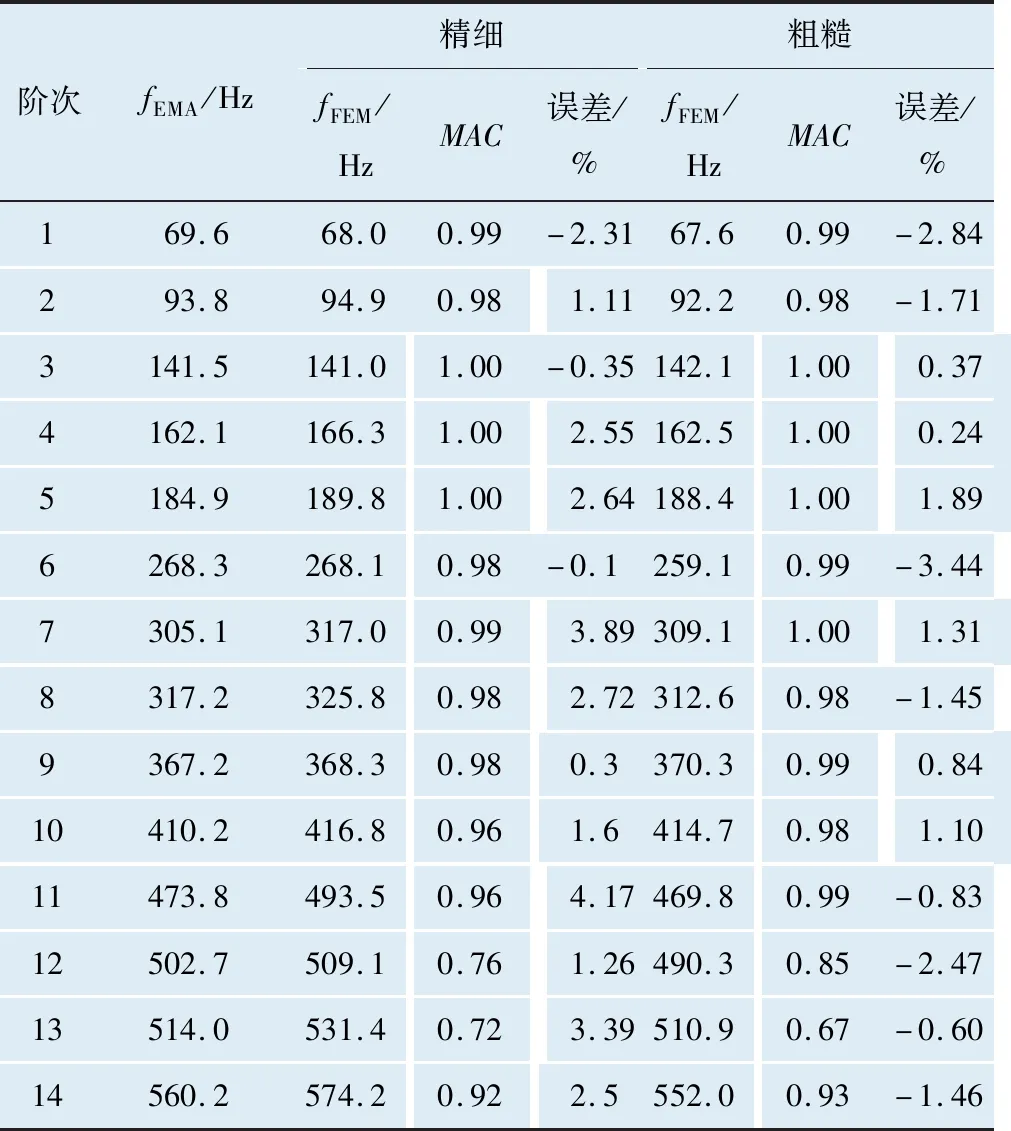
表3 有限元计算模态与试验模态匹配结果
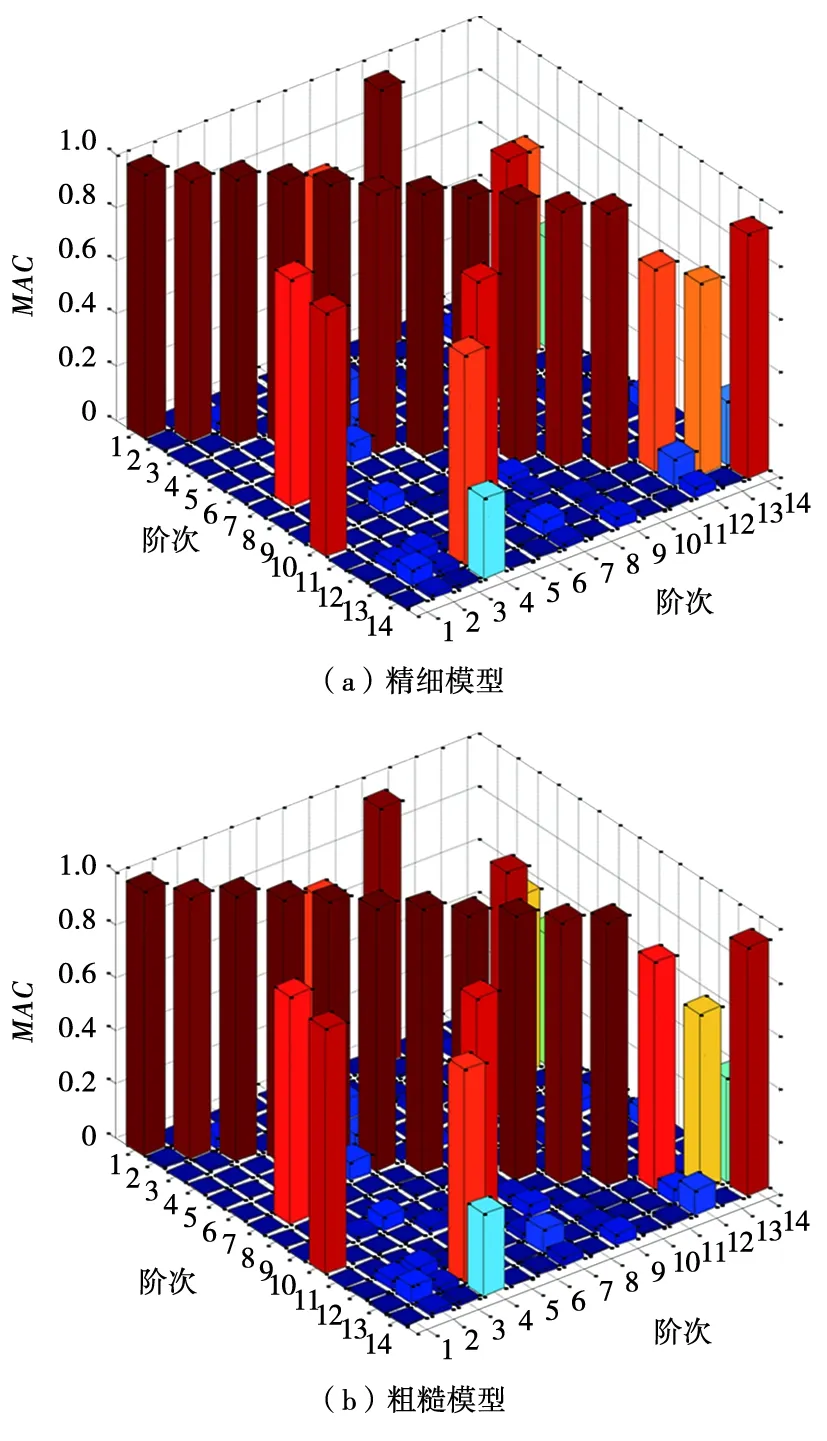
图8 有限元计算振型与试验振型MAC值匹配三维柱状图
在型材的前14阶模态中,有限元计算结果和模态试验结果的MAC值都比较高,频率误差都在5%以内。通过2种有限元模型计算结果和试验结果的比较可知,粗糙模型的模态频率误差更小,主要原因是粗糙模型在1.5 m方向的单元数量与试验测点数一致,与试验结果更加接近;采用长条形的粗糙模型并没有降低模态计算的精度,因此在大型型材有限元建模中,完全可以采用该方法降低模型单元数量,从而减小计算量。
3 有限元模型修正
在模型修正中,当特征量选取模态频率、模态频率+MAC值、模态频率+振型来对有限元模型进行修正时,如果要求修正以后的有限元模型能够充分、完整地复现试验数据,而且能够保证修正后的各阶振型保持正交,角度尽可能的大,那么特征量选择模态频率+MAC值修正的效果最好[12]。为了便于模型修正,将初始有限元模型进行修改,建立预修正模型。将型材的上下两层和中间层、焊缝层以及直筋分别采用不同的材料进行描述,将5个材料的弹性模量作为待修正参数,选择前14阶频率及对应的MAC值作为修正目标,采用QP优化方法进行迭代。E1~E5表示型材5种材料的弹性模量,为5个待修正参数,迭代修正结果如图9所示。从图9中可知,各参数迭代大约25步后基本收敛。
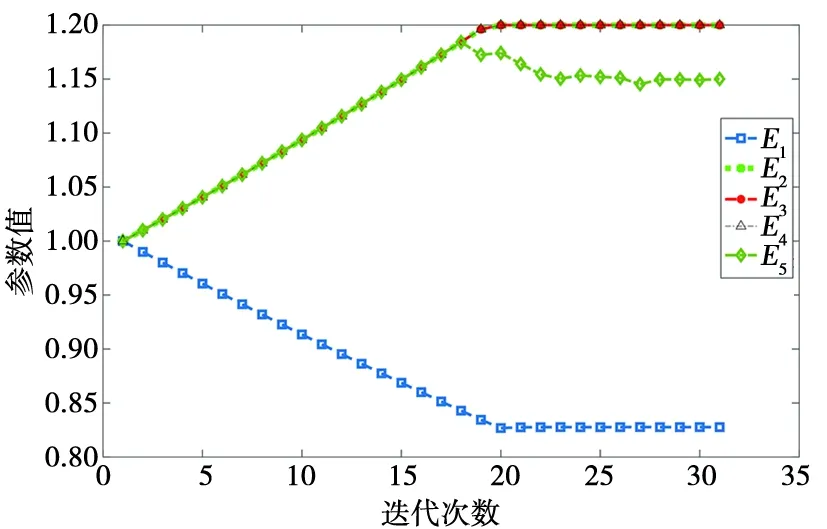
图9 参数修正迭代收敛图
同样对前14阶目标频率残差采用QP优化方法进行迭代修正,结果如图10所示。从图10中可以看出,各阶频率残差在迭代20步以后基本趋于收敛,误差最大的为第1阶模态频率残差,收敛后最大误差为-3.2%左右。各阶修正目标MAC值迭代结果如图11所示。从图11中可以看出,迭代修正过程中,除12阶MAC值略有降低外,其他各阶MAC值均有明显提高。
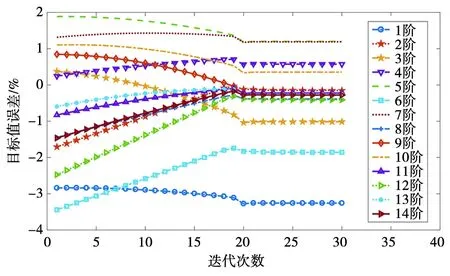
图10 各阶模态频率收敛情况

图11 各阶MAC值收敛情况
将有限元粗糙模型修正前后的MAC值与频率误差比较结果列于表4中。从比较结果可知,有限元模型频率初始误差最大为-3.44%,绝对平均误差为1.47%,修正后最大为-3.23%,绝对平均误差为0.82%;MAC值基本都有所提高,均值从修正前的0.95提高到修正后的0.96。
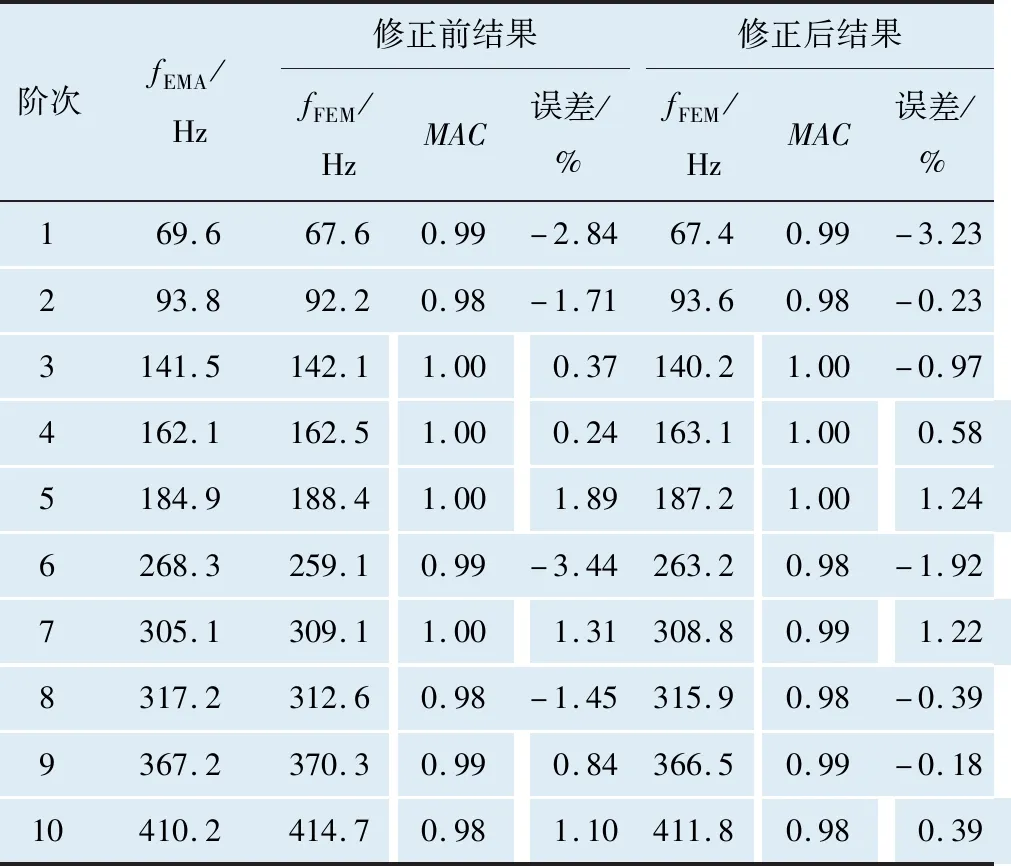
表4 粗糙模型修正前后有限元计算模态与试验模态匹配结果
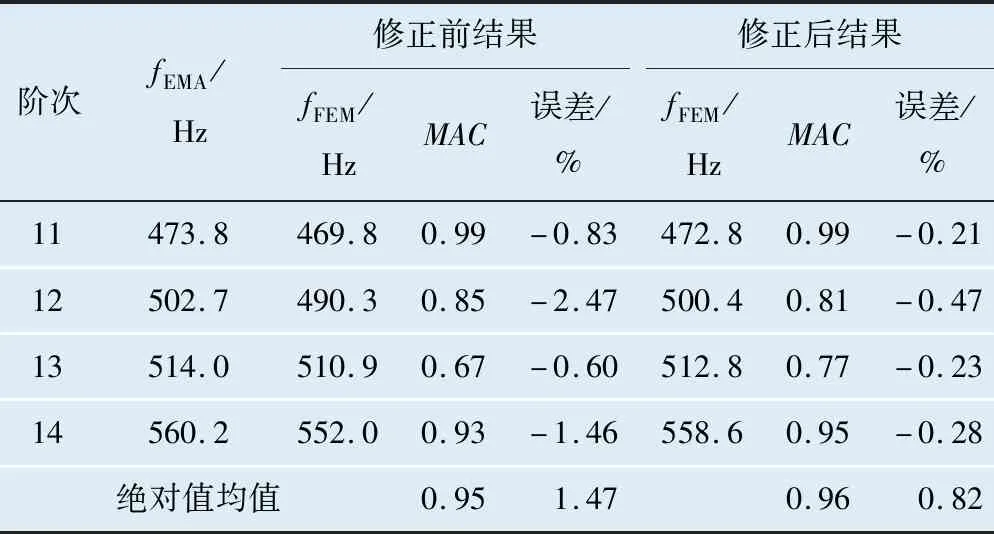
续表4
4 结论
(1) 本文对高速列车车体型材进行了2种不同的有限元模态计算,并对车体型材进行了试验模态测试。将2种有限元模态计算结果与试验模态测试结果进行了对比,由于粗糙模型在1.5 m方向的单元数量与试验测点数一致,所以粗糙模型计算的模态频率与试验模态测试结果更接近。
(2) 采用长条形单元的粗糙模型进行有限元模态计算并没有降低模态计算的精度,因此对于高速列车车体等大型结构进行有限元网格划分时,可以采用较为粗糙的单元来降低有限元模态分析计算量。
(3) 利用基于灵敏度分析的有限元模型修正方法对模型进行修正之后,得到了更高精度的等效有限元模型。模型修正后,前14阶的频率绝对平均误差均值由1.47%降到0.82%,MAC均值由0.95提高到0.96。可见,经过修正之后得到了更为准确的有限元模型。
