基于车内噪声控制目标的400 km/h高速列车车体隔声分配设计研究
2022-10-31韩铁礼邓琪云孟林林宋雷鸣
韩铁礼,邓琪云,王 凯,孟林林,宋雷鸣
(1.中车唐山机车车辆有限公司,河北 唐山 064000;2.北京交通大学 机械与电子控制工程学院,北京 100044)
高速列车运行速度的不断提高必然会导致车内噪声的急剧增加,为保障人们乘坐的舒适性,必须采取有效的措施降低车内噪声。在振动噪声相关领域,通过低噪声设计有效降低噪声是国内外学者广泛研究的课题。2003年,Huang Liangyu et al.通过建立汽车统计能量分析模型对动力系统空气噪声与道路噪声问题进行了声学包设计[1]。2007年,Davis et al.根据统计能量分析原理,利用不同声学材料的组合搭配来满足飞机舱室的声学设计要求[2]。2009年,Freeman et al.通过汽车的声学设计试验得出了车内声学设计的有关结论[3];杨宏 等则通过仿真计算出了车内噪声的设计目标值,并提出了有效的噪声控制措施[4]。2010年,沈艳祥 等从动车组车内噪声的设计理念出发对动车内进行噪声设计时着重考虑了声品质等心理声学的影响[5]。2012年,Gur et al.在不考虑成本的情况下,通过使用多种轻质玻璃材料来满足汽车NVH的设计要求[6]。2013年,车勇 等通过建立电动汽车的车内噪声预测模型,得出了车体各个区域对车内噪声的贡献值,然后针对贡献值较大的区域进行声学设计,以满足车内噪声设计要求[7]。2015年,张春岩基于混合有限元-统计能量分析(FE-SEA)方法求出了高速列车车体各结构声学参数对车内噪声的影响因子,为降低车内噪声提供了有效的指导[8]。2018年,Mosquera-Sanchez et al.为降低混合动力电动车车内噪声,从声品质要素进行综合设计,达到多目标声质量的平衡,从而降低车内噪声[9]。虽然针对车内低噪声设计的研究较为普遍,但大多数研究都是在车体已设计完成的情况下通过改进车体结构的声学参数来满足车内噪声设计要求,这种低噪声设计过程不仅耗时耗材,而且不利于创新。
本文从正向设计车内噪声的思路出发,以现有高速动车组实车为基础,通过试验获得了动车组车内噪声以及动车组车体隔声量等相关试验数据。基于试验数据的前提下,利用统计能量分析原理建立车内噪声预测模型,准确地预测出高速列车在400 km/h运行速度下的车内噪声。在需要提高车体隔声量的情况下,基于车体等辐射原理进行车体隔声量的最优分配,可避免车体设计过程中隔声性能出现设计不足或设计过度的问题。车体结构隔声量分配计算流程如图1所示。
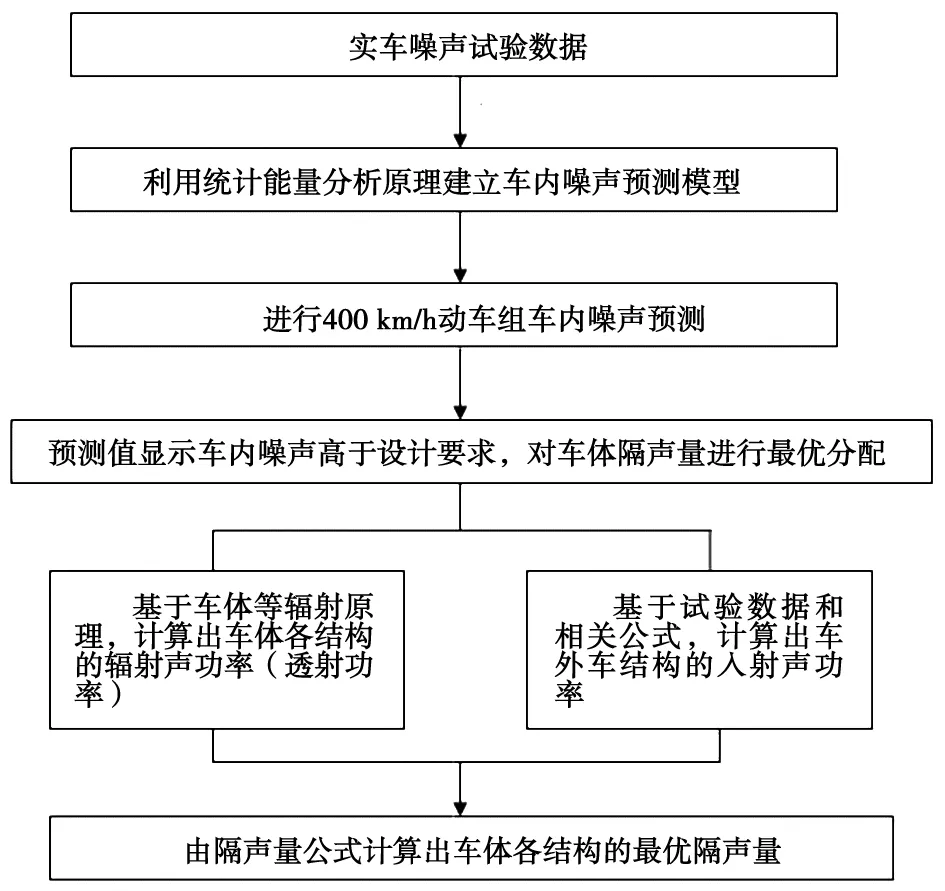
图1 车体结构隔声量分配计算流程
1 车内噪声预测原理
高速列车的结构尺寸大,噪声预测要求分析的频带范围宽,大多数计算分析方法在计算效率上很难满足工程的快速计算的要求,统计能量分析(Statistical Energy Analysis,简称SEA)计算的高效性,使得该分析方法成为高速列车车内噪声预测的主要方法之一。统计能量分析通过求解系统的功率流平衡方程得出系统对外界的响应,功率流平衡方程描述了子系统中能量损失以及能量流动之间的关系。一般情况下,子系统的共振模态性能都是相同的,系统平均能量响应的大小由输入系统的功率、系统内的功率损失以及子系统之间的功率交换之间的大小关系决定。图2给出了由2个子系统组成的系统中的功率流动和功率损失间的关系。
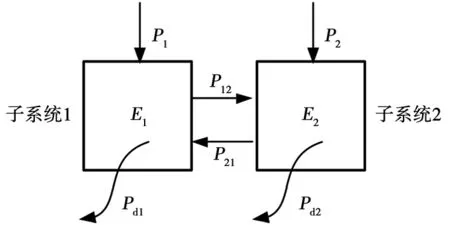
图2 双系统功率流动和功率损失关系
外界向子系统1输入的功率P1:
P1=Pd1+P12-P21
(1)
外界向子系统2输入的功率P2:
P2=Pd2+P21-P12
(2)
其中:Pd1=ωη1E1,Pd2=ωη2E2
(3)
P12=ωη12E1,P21=ωη21E2
(4)
式中:Pd1,Pd2——子系统1、子系统2流入外界的功率或自身的损耗功率;
P12——子系统1流入子系统2的功率;
P21——子系统2流入子系统1的功率;
ω——角频率;
η1,η2——子系统1、子系统2的自身损耗因子;
η12——功率由子系统1流入子系统2时的耦合损耗因子;
η21——功率由子系统2流入子系统1时的耦合损耗因子;
E1,E2——子系统1、子系统2内部的能量。
式(1)、式(2)还可用矩阵来表示:
(5)
由上可知,若一个系统由m个子系统组成,则其功率流平衡方程为:
(6)
(7)

图4 动车子声场设计示意图
式中:Pi——外界向子系统i输入的功率;
ηij——功率由子系统i流入子系统j时的耦合损耗因子;
ηi——子系统i的自身损耗因子;
Ei——子系统i内部的能量。
式(6)可简记为:
(8)
式中:[η]——子系统自身损耗因子矩阵;
{E}——子系统内部能量矩阵;
{P}——外界传递到子系统的输入功率矩阵。
因此,子系统内部储存的能量可表示为:
(9)
最后,根据声能密度相关公式,得出声学子系统i在分析频段的平均声压级SPLEi的表达式为:
(10)
式中:ρ0——空气密度;
c0——空气中的声速;
p0——参考声压;
Vi——子声场i的体积。
2 车内噪声预测
2.1 高速动车组车内噪声预测简化模型及验证
动车组车内噪声传递路径可简化为如图3所示的传递路径。由于动车组的密封性能比较好,不存在外部噪声通过泄漏进入车内的问题;车内空调噪声属于列车静态下的噪声,静态噪声不会影响列车在运行状态下的车内噪声。因此,动车组车内噪声主要由车外噪声经过车体隔声后透射进入车内以及车体结构振动的噪声向车内辐射引起。
根据现有高速动车组实车车内布局,将动车组的一节动车车内空间简化为5个子声场系统,其子声场划分如图4所示。图5给出了基于统计能量分析原理的车内子声场的功率流动关系图。

图3 动车组车内噪声传递路径图
基于上述模型及公式(6)建立简化的车内噪声统计能量分析关系式,并进行软件编程,进行车内噪声的初步预测评价,评价中的参数采用标准动车组的实车测试数据。在验证过程中,先对噪声源进行必要的修正,在求解统计能量分析方程组时对系数矩阵进行了正则化处理。图6和图7分别为在330 km/h 和370 km/h 运行速度下动车车内端部和中部三分之一倍频程噪声预测值与实测值的对比图。
可以看出,在330 km/h和370 km/h两个速度级的运行状态下,通过噪声预测模型预测出的车内噪声值与通过试验测得的实际车内A计权噪声值之间的差值均小于3 dB,由此可知所建立的车内噪声预测模型符合偏差要求,预测模型能够准确地反映出车内噪声状况。
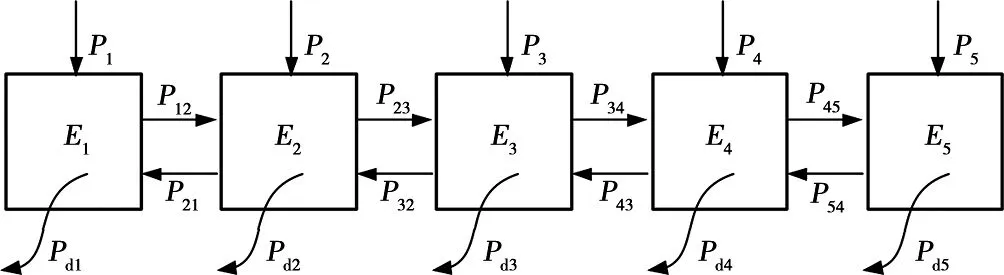
图5 基于统计能量分析原理的车内子声场功率流动关系图
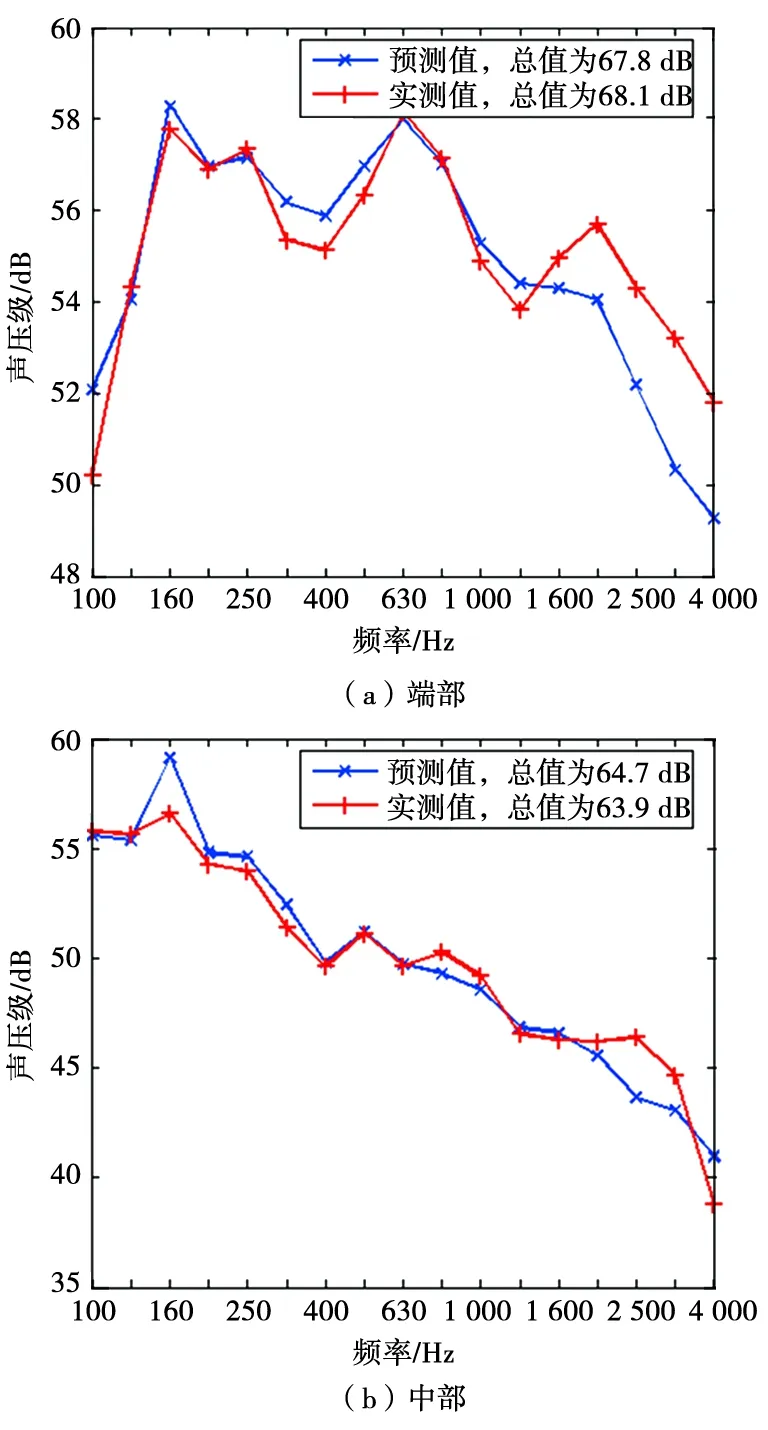
图6 330 km/h车内噪声预测值与实测值对比图

图7 370 km/h车内噪声预测值与实测值对比图
2.2 400 km/h动车组受电弓拖车车内噪声预测
基于标准动车组250 km/h、300 km/h、350 km/h、380 km/h速度下的运行试验测试数据,通过数据拟合外推,预测动车组在400 km/h速度下运行的噪声源及车内噪声。图8给出了400 km/h动车组受电弓拖车车内端部和中部的噪声预测结果。
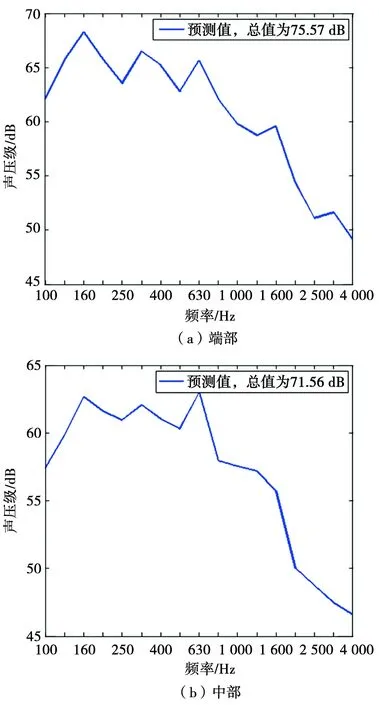
图8 400 km/h动车组受电弓拖车客室预测噪声的三分之一倍频程曲线
由图8可知,受电弓拖车车内端部噪声预测值为75.57 dB,噪声主要集中在中低频部分,在频率为160 Hz时出现峰值,峰值大小为68.21 dB,该峰值频率与动车组在试验运行时的峰值频率相同;中部噪声预测值为71.56 dB,在频率为630 Hz时出现峰值,峰值大小为62.96 dB,该峰值频率同样与试验运行时相同。由此表明动车组在400 km/h速度下车内噪声的预测值符合车内噪声频谱分布规律。
3 车体隔声量最优分配
根据国内高速列车车内噪声设计要求,400 km/h动车组车内端部噪声应不大于72 dB,车内中部噪声应不大于70 dB。由预测结果可知,受电弓拖车车内端部噪声值高于车内噪声设计要求值3.57 dB,中部噪声值高于设计要求值1.56 dB。因此,在设计400 km/h动车组时,基于车体等辐射原理对车体进行隔声量的最优分配,以有效提高受电弓拖车整车车体隔声量,不仅使车内噪声满足设计要求,而且可避免在车体设计过程中出现隔声量设计不足或设计过度的问题。
对于动车组车厢,当车外噪声经过车体四周隔声结构后,车体各结构向车内辐射的声功率都相等时,车体结构的隔声量达到最大。按图4的模型,将受电弓拖车车体分成5个区段,每一区段部件对车内辐射噪声的大小相同,图9给出了统计能量分析中某一子声场的结构尺寸示意图。

图9 子声场示意图
在计算过程中,该子声场内的声能密度被认为是均匀的,即该子声场内的声压级处处相等。根据400 km/h动车组车内噪声设计要求定义该子声场声压级目标值,由式(9)和式(10)计算出各子声场在给定内部声压级时的输入功率。
以车内某一子声场i为例,先求出车体各结构向子声场i内部输入的总功率,然后对包围该子声场的车体结构对子声场i内部辐射的声功率进行最优分配,具体计算过程如下。
(1) 车窗玻璃向子声场i内部辐射的最优声功率Pi1:
(11)
(2) 侧墙板向子声场i内部辐射的最优声功率Pi2:
(12)
(3) 顶板向子声场i内部辐射的最优声功率Pi3:
(13)
(4) 地板向子声场i内部辐射的最优声功率Pi4:
(14)
式中:PiT——车体各结构向子声场i内部输入的总功率;
a,b,c,d,e,f——分别为车体相关结构的尺寸。
在求得车体各结构向子声场辐射的最优声功率后,为了获得车体的最优隔声量,还需要知道车体各结构的入射声功率。车体各结构的入射声功率Wi根据车外声压实测数据由式(15)计算得出。
(15)
式中:pi——车外噪声声压的试验数据;
S——车体结构的面积。
最后由隔声量的计算公式(16)得出车体各结构的最优隔声量:
(16)
其中:
(17)
式中:TL——结构的隔声量;
τ——结构传递系数;
Wt——透射声功率。
图10和图11分别为受电弓拖车车体端部区域和中部区域隔声量的重新分配值与实测值的对比分析图。
由图10可知,受电弓拖车车体端部区域隔声量重新分配后,端部区域的地板在低频区的隔声量需要较大幅度的提高,在高频区的隔声量可以适当减少;端部区域的侧墙和车窗玻璃在低频区的隔声量则不需要提高,在高频区的隔声量则需要大幅度提高;端部区域的顶板在中频区的隔声量需要提高。由于隔声量是频率的函数,评价隔声量较为麻烦,因此国际标准化组织规定将计权隔声量RW作为评价隔声量的一种单值评价方法。通过计算计权隔声量,重新分配隔声量后端部地板RW值为58.9 dB,高于实测值3.1 dB;端部侧墙RW值为40.4 dB,低于实测值2.0 dB;端部车窗玻璃RW值为40.4 dB,低于实测值0.9 dB;端部顶板RW值为44.2 dB,高于实测值0.9 dB。
由图11可知,受电弓拖车车体中部区域隔声量重新分配后,除中部区域的地板在低中频区隔声量需要提高外,车体其他结构隔声量均低于其原隔声量。经分析可知,由于受电弓拖车噪声值在端部的超标值为3.57 dB,在中部的超标值为1.56 dB,车体隔声量重新分配之后端部噪声降幅较大,而中部噪声降幅较小,导致端部子声场向中部子声场传递的能量降低。隔声量重新分配后中部地板RW值为42.5 dB,高于实测值0.9 dB;中部侧墙RW值为39.4 dB,低于实测值3.0 dB;中部车窗玻璃RW值为39.4 dB,低于实测值1.9 dB;中部顶板RW值为42.7 dB,低于实测值0.6 dB。
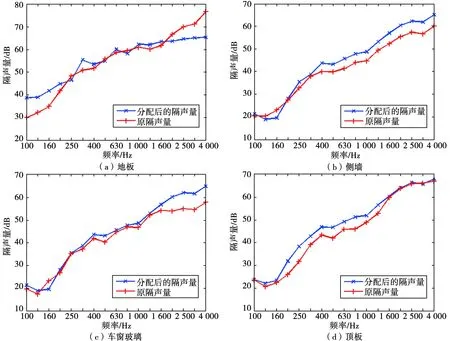
图10 受电弓拖车车体端部区域隔声量对比

图11 受电弓拖车车体中部区域隔声量对比
因此,为使400 km/h动车组车内噪声满足设计要求,动车组拖车端部地板的隔声量需提高3.1 dB,端部顶板的隔声量需提高0.9 dB,中部地板的隔声量需提高0.9 dB。另外,车体其他结构均可适当降低隔声量的要求。
4 结论
本文从正向设计车内噪声的思路出发,以现有高速动车组实车为基础,通过试验获得了动车组车内噪声以及动车组车体隔声量等相关试验数据。基于动车组噪声试验数据,利用统计能量分析原理建立车内噪声预测模型,准确地预测出400 km/h动车组的车内噪声。在需要提高车体隔声量的情况下,基于车体等辐射原理进行了车体隔声量的最优分配,不仅使车内噪声满足设计要求,而且避免了车体设计过程中隔声性能出现设计不足或设计过度的问题,完成了高速列车车内环境的低噪声设计。
