一类线性离散时间系统的预见控制器设计

李丽 孟晓华

(1.湖北经济学院统计与数学学院,湖北 武汉 430205;2.湖北经济学院中国改革试点探索与评估协同创新中心湖北分中心,湖北 武汉 430205)

1.引言

跟踪控制器的作用是使得系统的输出能紧紧跟随其希望的输出,而不消耗过多的控制能量.跟踪控制的问题一直是控制理论中一个研究的热点,而且也取得了很好的成果[1].在生活实际中有许多控制系统的输出目标值信号是已知的.例如X -Y工作台、机器人系统,其目标路径就是事先规定的,因而是已知的,或者说,是可以预见的.预见控制理论就是利用可预见的目标值信号的未来信息参与当前控制系统中,使得闭环系统的跟踪性能得到提高.[2]预见控制的思想最初起源于20世纪60年代.Sheridan于1966年在文[3]中介绍了预见控制的本质特征和三种基本模型,通过三个模型,提出了预见控制的概念.1968 年,Bender将线性最优预见控制的方法应用于车辆悬挂系统[4].Hayase和Ichikawa于1969年提出了利用目标值改善系统跟踪性能的预见控制方法[5].20 世纪70年代,以Tomizuka[6]、Katayama[7]为代表的学者们发表了一系列成果,这方面的研究才被人们广泛关注.随后基于这些@期经典预见控制理论方法,相关学者将预见控制理论进一步推广到线性奇异系统[8],随机系统[9],多智能体系统[10]等等.

不确定现象广泛存在,因此如何利用预见控制理论的方法处理鲁棒控制问题,近年来得到了高度的关注,尤其是H2/H∞预见控制问题.如文[11]引入H∞的控制思想,解决了连续线性系统的H∞前馈预见问题,并基于H∞代数Riccati方程最小化指标函数,得到最优控制律.随后该课题组利用Hamiltonian矩阵方法研究了一般形式的连续时滞H∞预见控制问题[12].线性矩阵不等式是鲁棒控制理论中一种有效的方法,并被应用到系统和控制的各个领域中.例如文[13]构造增广系统将带积分鲁棒预见跟踪控制问题转化为鲁棒LQ调节器问题,得到的控制器结构也包含预见前馈补偿器、状态反馈控制器和积分环节,来研究带执行器故障的离散时间多面体不确定系统的预见控制问题.文[14-15]将预见控制理论中经典的差分算子方法直接推广到参数不确定系统中来,并结合LMI 技术给出了鲁棒预见控制器的设计方法.另一方面,为了克服文[14-15]中的差分算子无法作用于时变的不确定项,文[16]利用系统状态与其稳态值之差代替通常的状态差分来构造扩大误差系统,通过求解LMI 来给出预见控制器的设计方法.

针对一类离散时间系统,本文将结合预见控制理论的方法和LMI技术,研究状态反馈和输出反馈预见控制器的设计问题.本文引入两个新的辅助变量,通过系统状态与辅助变量之差代替通常的状态差分来构造扩大误差系,改进了以往的误差系统的构造方法,得到一种新的扩大误差系统.然后,通过改写扩大误差系统的输出方程,使其融合未来预见信号的信息,并利用李亚普洛夫第二方法,给出保证闭环系统渐近稳定的条件.我们还将通过数值仿真对不同的预见步数的情况进行比较,显示出目标信号的预见作用对闭环系统跟踪性能的优越性.需要指出了是本文针对线性离散时间系统给出了一种新的扩大误差系统的构造方法.本文构造出扩大误差系统不含误差向量,这样处理的好处有两点: (i) 降低系统维数,减少计算量;(ii) 允许系统的输出方程中含有不确定项,应用对象更广泛.

记号:P ＞0表示P为对称正定矩阵,P ＞Q表示P -Q ＞0;*表示对称矩阵的对称项,I表示适当维数的单位矩阵.

2.问题描述及基本假设

考虑离散时间系统:

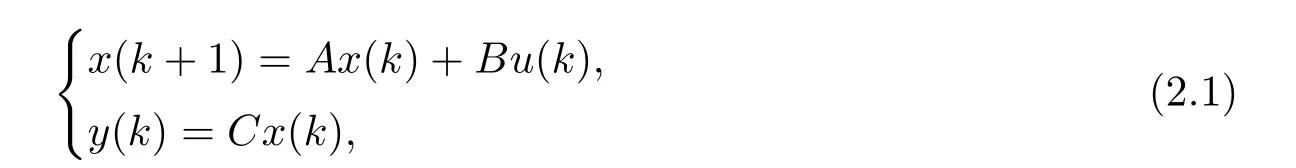
其中,x(k)∈Rn为状态向量;u(k)∈Rq为控制输入向量;y(k)∈Rq为控制输出向量;A,B和C为适当维数的常数矩阵.

设r(k)∈Rq为目标值信号.误差信号定义为

假设目标值信号是可预见的,即

假设A2设目标值信号r(k)的预见步数为MR,即在当前时刻k,目标值信号r(k),r(k+1),r(k+2),···,r(k+MR)为已知.并设MR步之后目标值信号不变,即

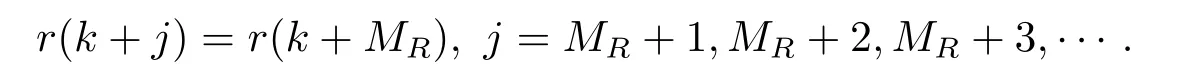
注2.1假设A2是预见控制理论的标准假设.按照控制系统本身的特点,只有一段时间的可预见目标值信号对系统的性能有较明显的影响,预见步数外的目标值信号为系统性能的影响不大,从而在可预见步数以外的目标值信号的值我们不必关心,从而可@为它是任何常数.事实上,普通的反馈控制系统不利用可预见信号,相当于取预见步数为零.

引理2.3针对系统x(k+1)=Ax(k),如果存在矩阵P ＞0及适当维数的矩阵G使得

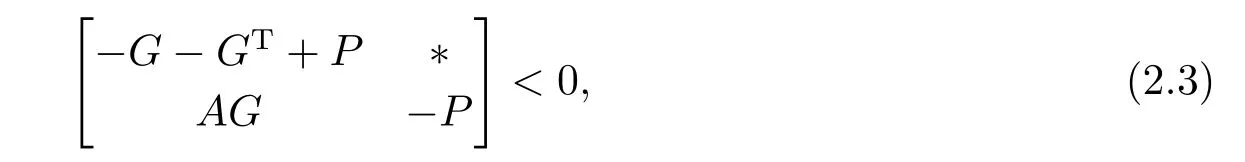
则系统是渐近稳定.

证根据文[19]的定理1,容易推出如果存在矩阵P ＞0,使得

则系统是鲁棒渐近稳定的.

对式(2.4)做合同变换: 左乘diag{GT,I},同时右乘它的转置可得到

而当H ＞0时,不等式-(L-H)TH-1(L-H)≤0成立,也就是

结合式(2.5)和式(2.6)可知,式(2.3)可以保证式(2.5)成立,而式(2.5)和式(2.4)是等价的.因此,若式(2.3)成立,则式(2.4)是成立的,从而结论成立.

受文[9]的启发,我们构造如下形式变量

3.扩大误差系统的推导

我们首先导出一个扩大误差系统,把这里的跟踪问题转化为调节问题,然后应用LMI技巧设计控制器.

根据式(2.1),式(2.7)和式(2.8)得到

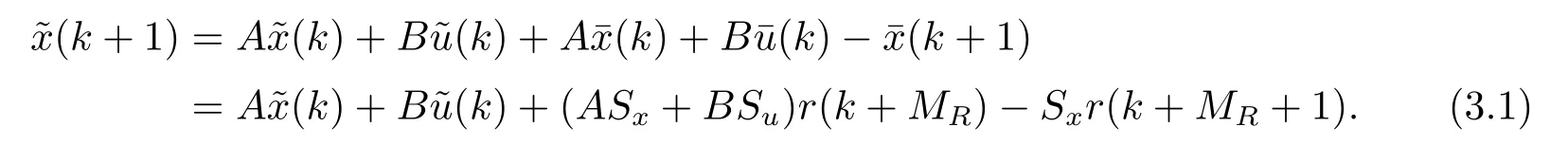
根据假设A2和式(2.8),上式可进一步写为

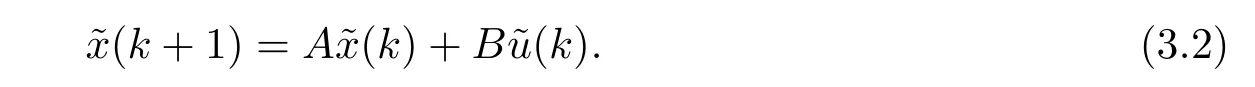
同时注意

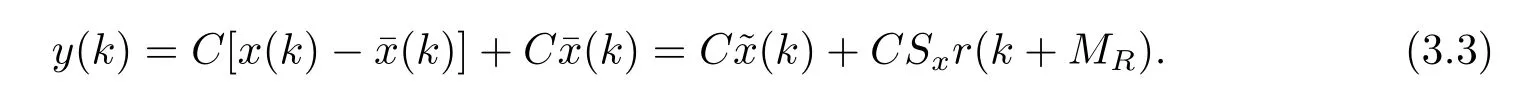
注意系统(3.7)的特点是: 体现预见信息的XR(k)是状态向量的一部分,这样形式系统(3.7)便包含了可预见的目标值的信息.但系统(3.7)中没有出现u(k)的差分,而只出现(k),这使得当利用LMI方法求出系统(3.7)的控制输入时,其中不会包含误差e(k)的积分,从而闭环系统不包含积分器,因此不利于消除静态误差.为此,我们引进离散积分器,它由下式定义

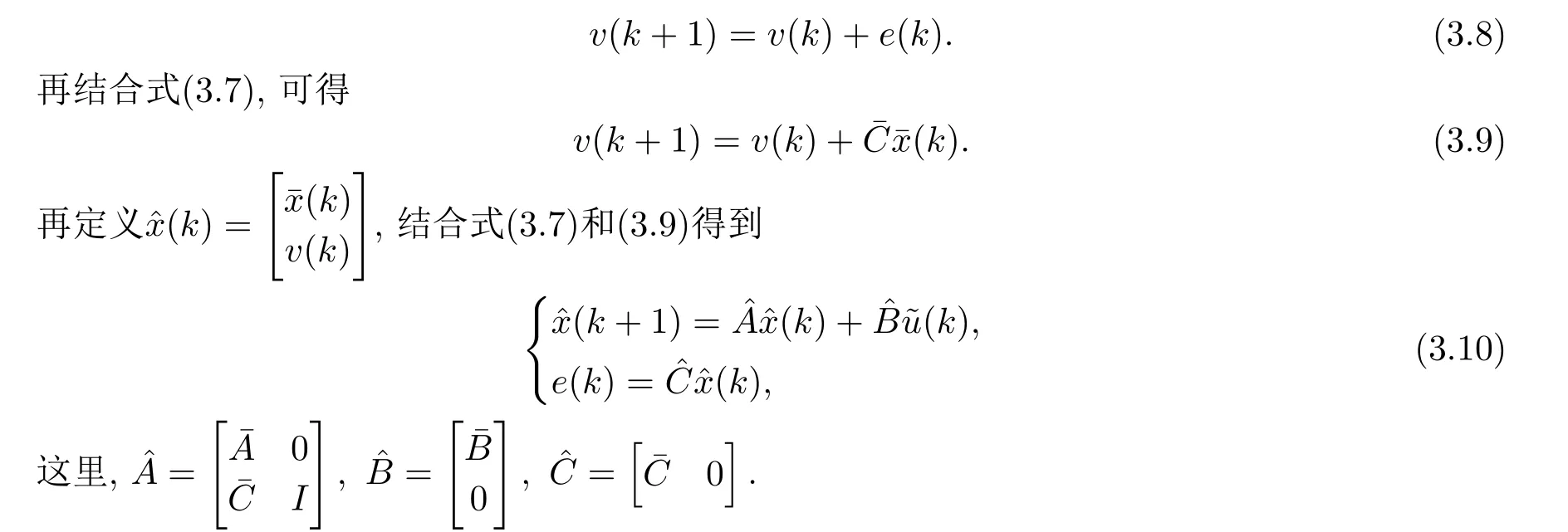
注3.1在构造扩大误差系统(3.10),在计算式(3.1)和(3.5)时并没有用到y(k)和x(k)的差分,而是通过引入辅助变量方法,这样给预见控制理论中线性离散时间系统的扩大误差系统的构造提供一种新的方法.另外,由于无需对系统(2.1)的状态方程两边取差分,因而避免了求系统的有关系数矩阵的差分,这使得即使系数矩阵是时变的,其形式系统(3.10)仍然有比较简单的形式.

注3.2和文[16]相比,状态变量(k)中没有加入误差向量e(k),这样处理不仅减少扩大误差系统的阶数,降低计算复杂度.

4.预见控制器的设计

针对扩大误差系统(3.10),本节分别设计状态反馈控制器和输出反馈控制器,分割代回原系统便得到带有预见作用的状态控制器和输出控制器.

成立,则闭环系统(4.2)是渐近稳定的,其中状态反馈增益矩阵为K=YG-1,控制输入为

证我们来证明: 对于闭环系统(4.2),如果定理4.1的条件成立,则引理2.3的条件也成立,从而由引理2.3可知定理4.1成立.

根据引理2.3,如果存在一个矩阵P ＞0和矩阵K,使得矩阵K矩阵P满足

现在来研究系统(2.1)的带有预见作用的状态控制输入.

当假设A1,A2成立时,已经求得系统(3.10)的控制输入(4.1).对增益矩阵K进行分解

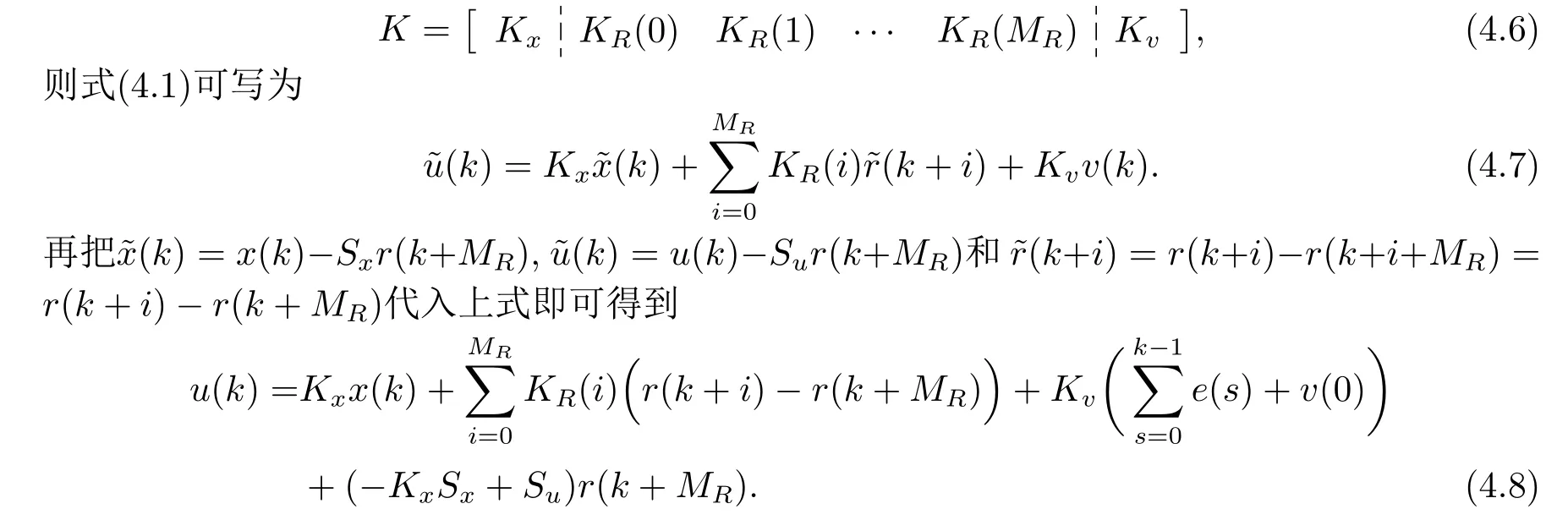
由上式看出,系统(2.1)的带有预见作用的控制器由4部分构成: 第1部分为状态变量反馈项;第2部分为基于未来目标值信号的预见前馈补偿项;第3部分是跟踪误差的积分;第4部分是关于初值和终值的补偿.

考虑到系统(2.1)的观测方程和目标值信号r(k)的可预见性,针对形式系统(3.10),观测方程取为

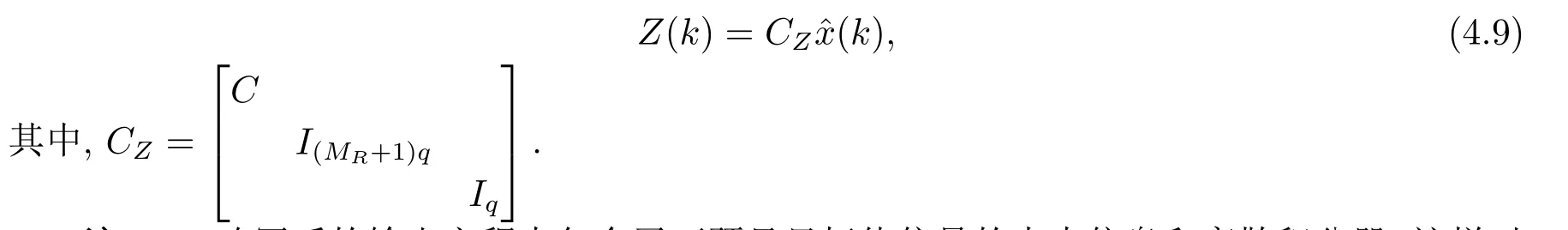
注4.2改写后的输出方程中包含了可预见目标值信号的未来信息和离散积分器,这样对系统(3.10)引入输出反馈时,控制输入带有预见作用和积分器,实现改善闭环系统跟踪性能和消除静态误差的作用.

假设系统(3.10)的控制输入为

那么当控制输入由(4.10)确定时,系统(3.10)的闭环系统为

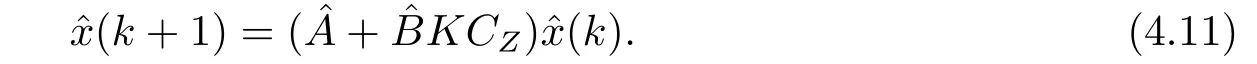
定理4.2对于给定的参数β和矩阵Q,如果存在矩阵P ＞0和矩阵G,U及L使得

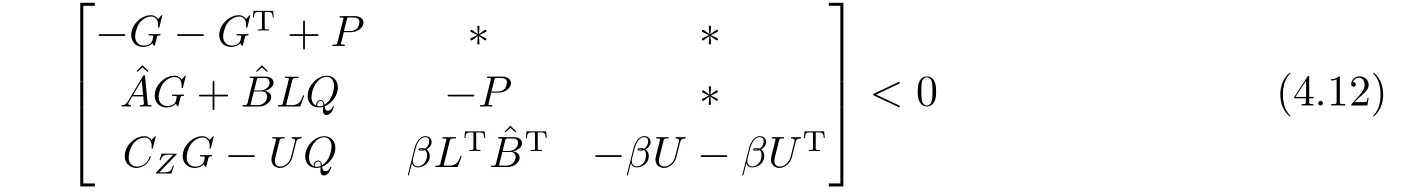
成立,则闭环系统(4.11)是渐近稳定的,其中静态输出反馈增益矩阵为K=LU-1,控制输入为

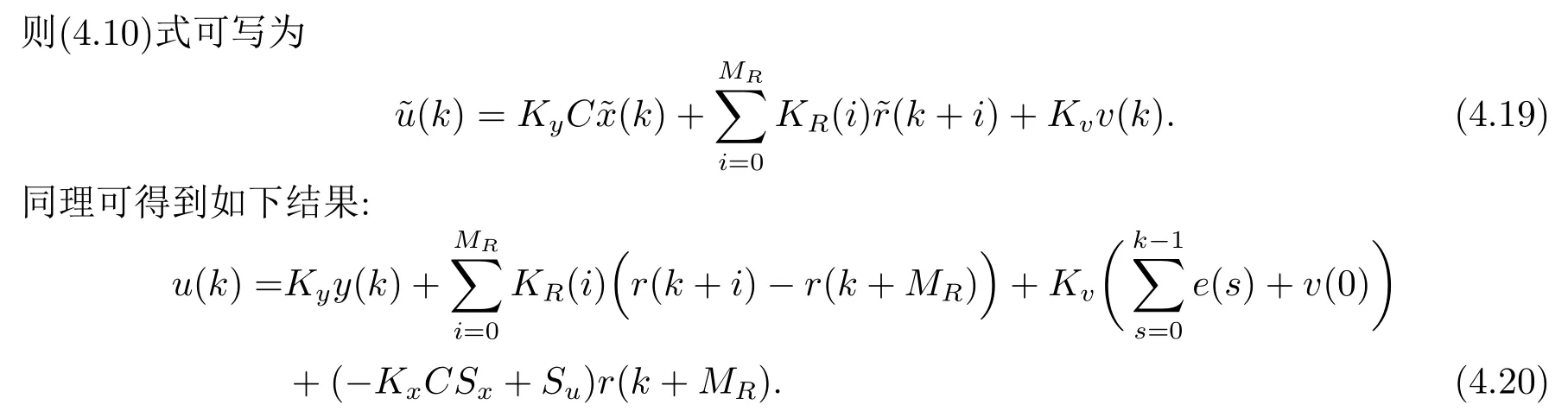
由上式看出,系统(2.1)的带有预见作用的控制器由4部分构成: 第1部分为输出反馈项;第2部分为基于未来目标值信号的预见前馈补偿项;第3部分是跟踪误差的积分;第4部分是关于初值和终值的补偿.

5.数值仿真

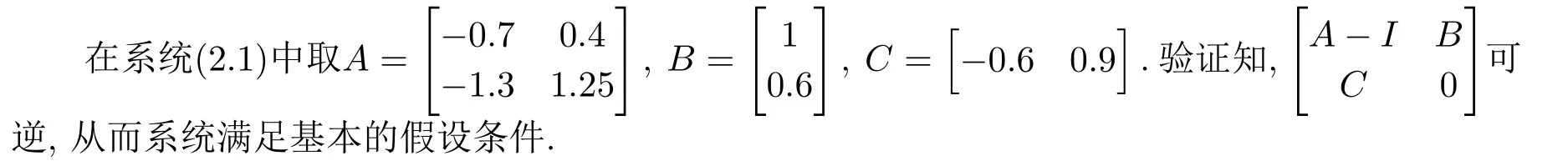
我们对目标值信号的预见步数分别为MR=2和MR=6及目标值信号没有预见即MR=0三种情况进行数值仿真.根据定理4.1,应用MATLAB的LMI工具箱可求解出LMI(4.3)中的矩阵变量G和Y,则反馈矩阵K=YG-1自然就得到.

图5.1给出了系统(2.1)的闭环系统的输出响应,图5.2是跟踪误差.可以看出在目标值信号的预见步长为MR=6和MR=2及目标值信号没有预见即MR=0三种情况下,输出信号都能准确地跟踪目标值信号.但是随着目标值预见步长的增加,跟踪误差和输入峰值在减小,而且闭环系统的输出能更快跟踪目标值信号.这正是预见控制要达到的目的.

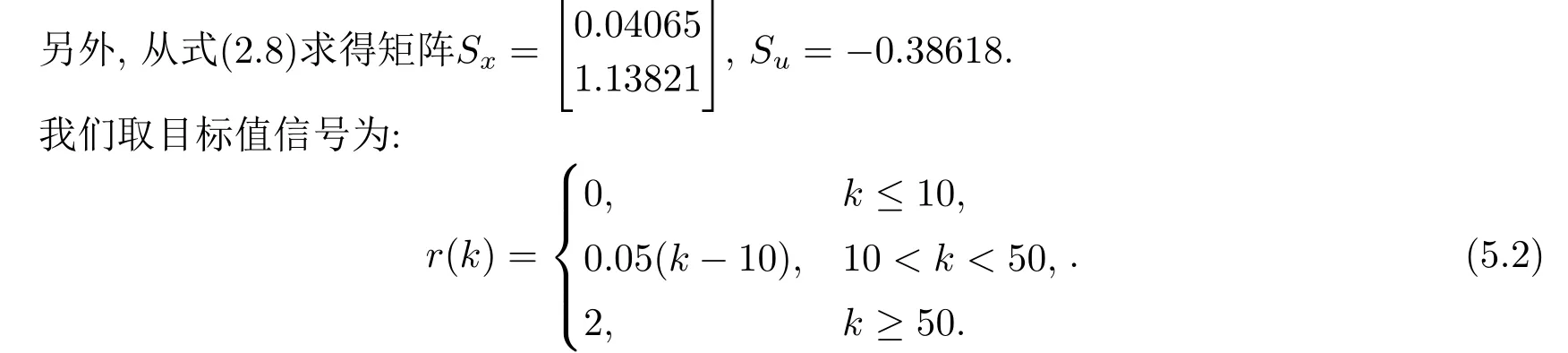
为了更好地研究预见补偿对系统的跟踪性能的效果,我们针对目标值信号(5.2)就预见步数为MR=3和MR=1及目标值信号没有预见即MR=0这三种情况进行数值仿真.图5.3给出闭环系统的输出响应,图5.4是跟踪误差.从图5.3和图5.4可看出,针对所选定的目标值信号,带有预见作用的控制器的跟踪效果明显好于不带预见作用的控制器的情况.而且随着预见步数的增加(从MR=1到MR=3),超调量和跟踪误差都减少.

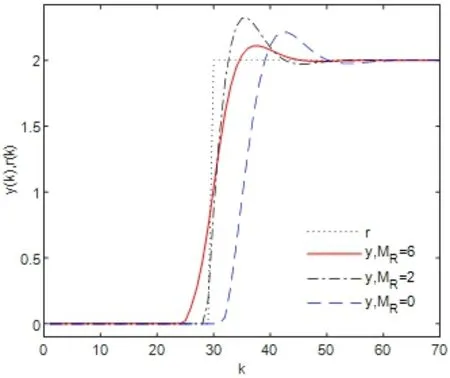
图5.1 MR不相同时,闭环系统的输出响应

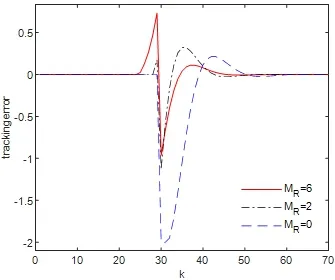
图5.2 MR不相同时,闭环系统的跟踪误差

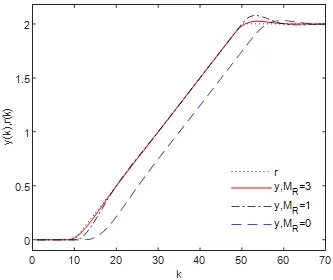
图5.3 MR不相同时,闭环系统的输出响应

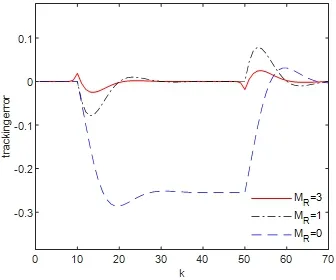
图5.4 MR不相同时,闭环系统的跟踪误差

下面针对输出反馈情况,取Q=CZ和β=1.我们针对以下三种情况进行数值仿真：①MR=6;②MR=2;③MR=0的情况进行比较.

根据定理4.2,应用MATLAB的LMI工具箱可求解出LMI(4.12)中的矩阵变量L和U,则反馈矩阵K=LU-1自然就得到.

作为例子,图5.5 和图5.6 表示预见步长为MR=0,MR=2和MR=6的输出响应和跟踪误差.通过比较采用预见控制和不采用预见控制两种情形下的跟踪曲线和相应的误差曲线,可以发现,当采用预见控制时,超调量明显减小了,而且可以更快地达到稳定状态.

同样,对于给定形如目标值信号(5.2)的情况,我们针对不同预见步长进行了数值仿真.图5.7表示在预见步数为MR=0,MR=1和MR=3时闭环系统的输出响应.图5.8是相应的跟踪误差.从图上看出,这三种情况的输出都能很好的实现对目标值信号的跟踪.然而不难看出MR=1和MR=3的跟踪效果明显好于不带预见的情况.而且,随着预见步长的增加,闭环系统能更加快速跟踪目标值信号.

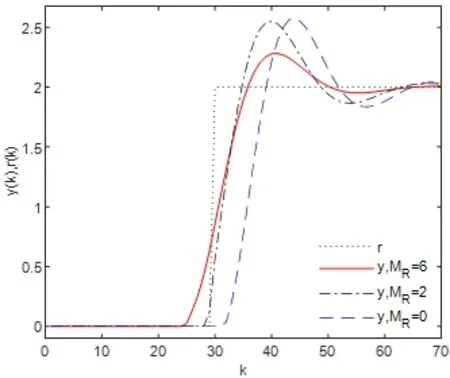
图5.5 MR不同时,闭环系统的输出响应

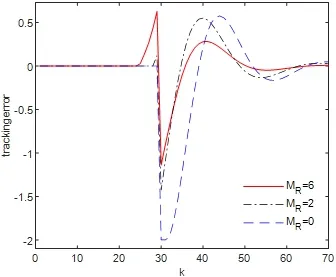
图5.6 MR不同时,闭环系统的跟踪控制

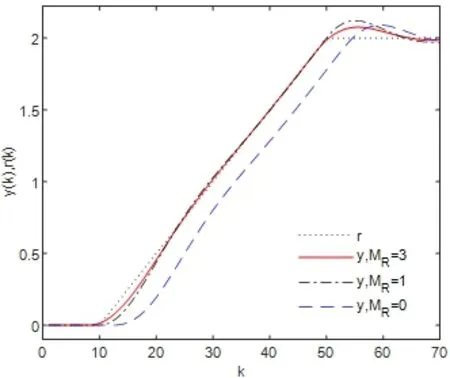
图5.7 MR不同时,闭环系统的输出响应

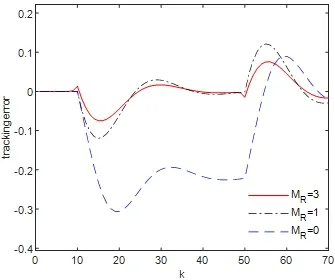
图5.8 MR不同时,闭环系统的跟踪误差

6.结束语

本文研究了离散时间系统基于线性矩阵不等式的预见控制问题.首先利用系统状态与辅助变量之差代替通常的状态差分做法推导出扩大误差系统,使得状态变量中融合可预见的目标值信号.然后,分别引入状态反馈和输出反馈,利用Lyapunov第二方法,给出了控制器存在的条件及设计方法,最后,通过求解一个LMI得到反馈增益矩阵.本文利用LMI理论来研究预见控制问题的方法是可以推广到周期时变系统的预见控制问题中去.最后的仿真实例说明了本文控制器的有效性.