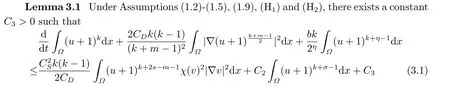Global Boundedness to a Quasilinear Attraction-repulsion with Nonlinear Diffusion
2022-10-31YANLijun闫利君WANGQing王清
YAN Lijun(闫利君),WANG Qing(王清)
(School of Science,North China Institute of Science and Technology,Sanhe 065201,China)
Abstract:In this paper,we deal with the quasilinear attraction-repulsion model with homogeneous Neumann boundary conditions.Let the chemotactic sensitivity χ(v) and ξ(w) be nonlinear functions.We prove that the system has a unique globally bounded classical solution under some assumptions.
Key words:Attraction-repulsion;Boundedness;Nonlinear sensitivity;Logistic source
1.Introduction
In this paper,we consider a quasilinear attraction-repulsion chemotaxis system with nonlinear sensitivity and logistic source

Hereχ0is the strength of the attraction andξ0is the strength of the repulsion.u(x,t),v(x,t) andw(x,t) denote the cell density,the concentration of the chemoattractant and the concentration of the chemorepellent,respectively.The nonlinearities

Chemotaxis describes the oriented movement of cells along the concentration gradient of a chemical signal produced by cells.The prototype of the chemotaxis model known as the Keller-Segel model was first proposed by Keller and Segel[7] in 1970:

Indeed,several findings have indicated thatχ=χ(v) has a significant regularizing effect in the presence of suitable decay asv →∞.

It is observed that the nonlinear diffusion of the cells is the other important mechanism to avoid cell aggregation.In particular,the focus is mainly on the competition between the chemotactic term and nonlinear diffusion term or logistic term in the cell equation.The initial-boundary value problem for the related system

Whenχ(v)andξ(w)are positive parameters in(1.8),ZHANG and LI[19]proved a globally bounded classical solution withD(u)=1,f(u) satisfy (1.4) and one of the following holds:

WANG[15]deduced a unique global bounded classical solution withD(u) satisfies (1.3) andf(u) satisfies (1.4).
When inχ(v) andξ(w) are positive functions in (1.8),WU and WU[16]asserted the global classical solutions,they obtained the important estimate of∫Ω|∇v|2dxwithD(u)satisfy (1.3) andf(u)=0.It is noticed that this method is not applicable for the generalf(u)in our paper.TAO and WANG[17]investigated the global boundedness of the solution in high-dimensions withD(u)=1,f(u)=0 and repulsion prevails over attraction,if attraction prevails over repulsion,blowup of solutions was identified inR2.JIN[4]deduced the global existence of classical solutions in two dimensions and weak solutions in three dimensions with large initial data,in which the results of [13] were improved.SHI and WANG[11]asserted a global bounded solution withD(u)=1,f(u)=0 and the repulsion prevails over the attraction,if the attraction prevails over the repulsion,they constructed the finite time blowup may occur in two dimensions;moreover,they presented the smoothness of the solution and its decay rates.
Motivated by [15-17],the purpose of this work is to show a unique globally bounded classical solution for chemotactic sensitivityχ(v) andξ(w) be nonlinear functions.Our main results are given as follows.
Theorem 1.1Assume that (1.2)-(1.5),(H1) and (H2) are valid.Moreover,suppose that

Obviously,Theorem 1.1 covers the criteria for (1.7) obtained in [14] as its special case in the model (1.1).
2.Useful Lemmas
The local existence and uniqueness of system (1.1) can be derived from the reason of Lemma 2.1 in [8],so we only state the result and omit its proof here.
Lemma 2.1[16]Suppose that(1.2)-(1.5)are valid.Then there exist a maximal existence timeTmax∈(0,+∞] and a unique couple (u,v,w) of functions,which satisfy
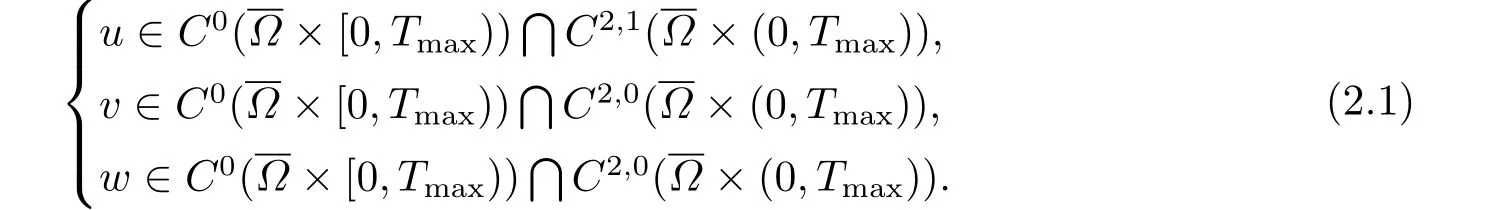
IfTmax<+∞,then


3.A Priori Estimates