Infinitely Many Sign-changing Solutions for a Quasilinear Choquard Equation

YANG Lu(杨璐),LIU Xiangqing(刘祥清)

(School of Mathematics,Yunnan Normal University,Kunming 650500,China)

Abstract:In this paper,by using the methods of perturbation and invariant sets of descending flow,we obtain the existence of infinitely many sign-changing solutions of a subcritical quasilinear Choquard equation in RN.

Key words:Subcritical quasilinear Choquard equation;The perturbation method;Sign-changing solution

1.Introduction

In this paper,we consider the following quasilinear Choquard equation

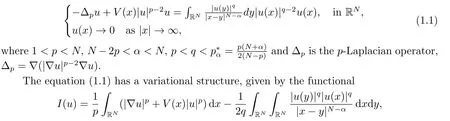
which appears in various fields of mathematical physics,such as quantum mechanics,physics of laser beams and the physics of multiple-particle systems.ForN=3,α=p=q=2,the equation (1.1) turns to be the well-known Choquard-Pekar equation,

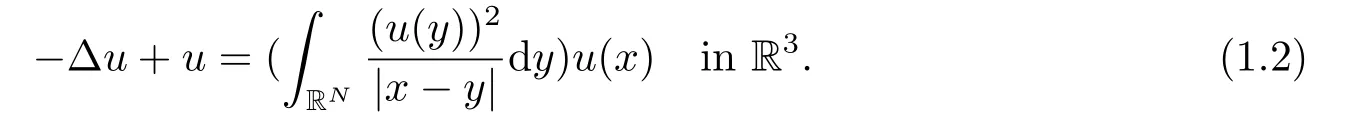
As early as 1954,it was proposed by Pekar[1]on quantum theory of polaron at rest.And it is an approximation to Hartree-Fock theory for one-component plasma[2].Ifuis a solution of the equation (1.2),thenΨ(t,x)=eitu(x) is a solitary wave of the following Hartree equation[3],

Whenp=2,(1.1) becomes a nonlinear Choquard equation,

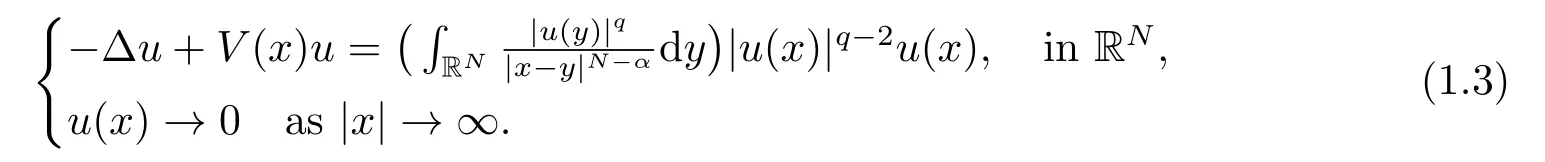
In the past several years,the existence of positive solutions,ground states,semiclassical state have been studied by many researchers.[4-6,17-21]But there are only a few results for the existence of solutions of quasilinear Choquard equations.Alves and YANG[7]proved the existence,multiplicity,and concentration of solutions of the semiclassical form of the equation (1.1) by variational methods.Lee et al.[8]proved the existence of weak solutions of the equation(1.1)by the mountain pass theorem and the fountain theorem.LIN,CHENG and TANG[9]proved the existence of the ground states of the equation(1.1)and whenp=2,N=3 by a variant variational identity and a constraint set,they proved the existence of a nonradially symmetric solution.

In recent years,there are some studies on the existence of sign-changing solutions of Choquard equations.Clapp and Salazar[10]proved the equation (1.1) has a positive solution and multiple sign-changing solutions in the symmetric domainΩwhenp=2,but the region considered here is only symmetric regionΩandΩ/=RN.Casani,Van Schaftingen and ZHANG[11]proved the equation (1.1) (p=2) has a sign-changing solution in the case ofwhenN=4 orN=＜α ＜3.However,there is no result of infinitely signchanging solutions of quasilinear Choquard equations in RN.So we consider the existence of infinitely sing-changing solutions of the equation (1.1).

We make the following condition on the potential functionV:

Theorem 1.1Assume 12p ＜α ＜Nand (V) hold.Then the equation (1.1) has infinitely many sign-changing solutions.

The paper is organized as follows.In Section 2 we collect elementary properties of auxiliary functions and verify the Palais-Smale condition for the functionalΓλ.In Section 3 we prove the existence of sign-changing solutions of the equation (1.1),i.e.,Theorem 1.1.

2.The Palais-Smale Condition

In this section,we first collect elementary properties of the Choquard term,and then proveΓλsatisfies the Palais-Smale condition.

3.The Proof of Theorem 1.1