二自由度柱面可展机构运动类型的分析

庄彦帅，张帆，王锋，张玉辉，张锐浩

（201620 上海市 上海工程技术大学 机械与汽车工程学院）

0 引言

可展曲面在一些领域有广泛的应用空间[1-3]，在船舶制造领域，将钢板加工成单向弯曲的可展曲面形状的可行性很高。JULIE[4]等讨论了基于边界线的船体可展曲面造型；郑玉健[5]等提出一种基于边界曲线的拟可展曲面构造方法应用在船体造型设计。在建筑设计领域，可展曲面同样具有很重要的研究意义[6]，设计师仅通过简单的加工程序便可得到预期的建筑效果。王峥涛[7]等对可展曲面的特性和应用实例进行讨论，并列举在造型生成阶段主要使用的两种可展曲面交互建模方法。可展曲面与工程设计建立起了联系，但侧重点均为直接利用可展曲面进行造型设计，对于可展曲面衍生的机构缺乏分析。NELSON[8]等将可展曲面进行组合，设计了一种滚动接触机构，演示了滚动机构的运动路径，通过组合得到滚动机构。除此之外，在可展曲面的基础上衍生了可展机构。GREENWOOD[9]等介绍了可展机构的一种运动类型分类方式，提出了阴影法来图解单自由度圆柱可展机构；HYATT[10]等利用投影角的性质得到球面四杆机构的面锥角，提出了四杆机构位置分析的替代方法；NELSON[11]等在圆柱面上建立切比雪夫四杆机构和可驱动的4R圆柱可展机构，证明了其步行或主动抓取运动。

由于可展机构具有良好的运动性能，越来越多的研究者分析可展机构的运动情况，提供了研究可展机构运动的思路方法，但提出的分析方法对于多自由度的可展机构，并不能完全适用。目前，研究对象主要集中在单自由度的4R 可展机构，或将常用的单自由度机构为基础框架设计可展机构，在多自由度可展机构的设计方面还鲜有涉及。本文以二自由度柱面5R 可展机构为模型，在可展机构的研究方法上进行了改进，可以实现单自由度到二自由度可展机构的分析。利用相对运动图解法与瞬时中心参考线法结合的方法，判断杆件的位置，通过杆件瞬时中心参考线的位置得到预想机构的运动，并分析了驱动方向来判断可展机构的运动类型，基于ADAMS 进行4 种情况的仿真验证。此种方法避免了在直接建模分析的繁琐过程中的错误，而且可以拓展到二自由度锥面可展机构来判断运动类型，为基于可展机构的二自由度机器人研究提供运动分析的理论依据。

1 可展曲面的基本理论

直纹曲面因具有良好的特性，在微分几何中占有重要地位，可展曲面便是直纹曲面中的一种。

1.1 直纹曲面

直纹曲面是由单参数直线族所生成的曲面，曲面S 的参数方程为

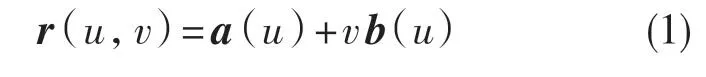
式中：a（u）——直纹曲面上准线的位置向量；b（u）——直纹曲面母线的单位向量。则曲面S 被称为直纹曲面[12]。

如图1所示，设直纹曲面的准线为曲线C：a=a（u），b（u）是过准线上一点 a（u）处的直母线上的单位向量，其中准线上的点 a（u）到过该 a（u）的直母线上P点的距离为v。

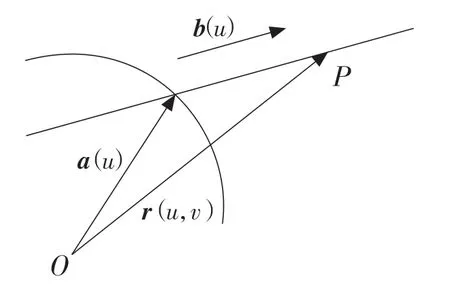
图1 直纹曲面Fig.1 Ruled surface

1.2 可展曲面

直纹曲面参数方程r（u，v）=a（u）+vb（u），若直纹曲面S 满足（a'（u），b（u），b'（u））=0，则该直纹曲面S 为可展曲面，其中，a'（u）、b'（u）分别为a（u）与b（u）的切向量，（a'（u），b（u），b'（u））=0 表示a'（u）、b（u）和b'（u）的混合积等于零。直观来讲，如果沿着直纹曲面的每一条直母线只有一个切平面，或者沿着直母线有同一法向量，则称该直纹曲面为可展曲面[13]。可展曲面可分3 种类型：柱面、锥面和一空间曲线的切线曲面，形成条件如下[14]：

当b（u）=b0为常向量时，任意母线的方向不变，曲面S 为柱面；当a（u）=a0为常向量时，任意母线过一定点，曲面S 为锥面；当b（u）=α为导线上切向量，或当a'（u）∥b（u）时，曲面S 为一空间曲线的切线曲面。

2 可展机构

2.1 可展机构基本理论

满足如下3 条准则的机构被定义为可展机构[11]：（1）当机构以零厚度建模时，该机构包含在可展曲面内或者符合可展曲面与其一致，如图2、图3所示；（2）该机构具有可动性；（3）不需要可展曲面变形便能使机构运动。

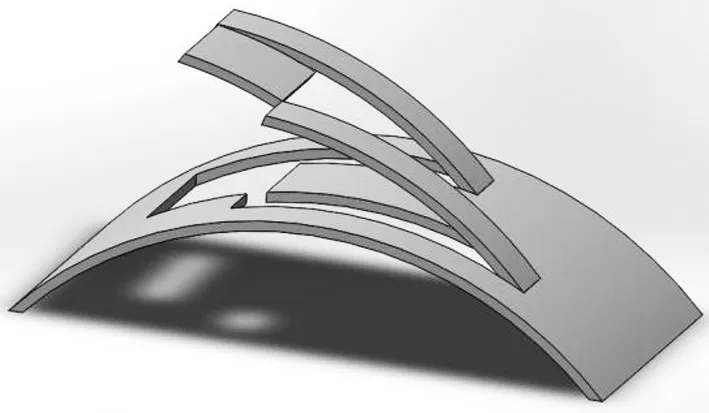
图2 包含在柱面内的四杆机构Fig.2 Four-bar mechanism contained in the cylinder

图3 符合柱面的四杆机构Fig.3 Four-bar mechanism conforming to cylinder

在准则（2）中，通过螺旋理论求得机构自由度便能判断出机构的可动性。准则（1）与准则（3）可以得出机构转动关节轴的放置条件，即可展机构是通过可展曲面的直母线对齐旋转关节轴来实现的，这称为关节轴约束条件，利用此条件便可将不同机构部署于可展曲面上。可展机构要求所有连杆要与基准表面一致并与基准表面对齐。基准表面就是机构所在的可展曲面，机构的转动关节轴必须与可展曲面的直母线对齐。图2 所示类型为包含在可展曲面内的可展机构。当厚度不可忽略时，对于符合可展曲面的可展机构，其中关节轴位于一个可展曲面上，与它所符合的另一个可展曲面偏移，关节轴需要与偏移的可展曲面上的直母线对齐。如图3所示得到的4R 可展机构。

机构的运动学分析只依赖于关节的相对位置，连杆可以是任意形状的，因此只要不发生自干涉，刚性连杆的相对运动与连杆形状无关。确保可展机构连杆可以包含在可展曲面内或符合可展曲面上利用的就是这一基本原理，机构的连杆可以形成可展曲面的形状。

2.2 可展机构的运动类型

由于可展机构符合或者包含于可展曲面内，因此预测可展机构相对于可展曲面的参考表面运动是十分重要的，尤其是在一致位置时的运动。GREENWOOD 定义了可展机构3 种运动分类[9]：

内移动性：当可展机构从一致位置运动时，它可以完全进入（或保留在）参考表面内部的能力。

外移动性：当可展机构从一致位置运动时，它可以完全进入（或保持在）参考表面外部的能力。

跨内外移动性：当可展机构从一致位置运动时，它可以同时进入参考表面的内部和外部的能力。

这种分类的优点在于可以判断从参考表面一致位置时开始运动，可展机构是否完全或部分进入可展曲面的内部还是外部，可以预测可展机构的运动范围，对设计可展机构相对一致位置时是非常便利的。当选择的驱动方向不同，移动性也会发生改变，因此驱动的选择会实现设计所需的运动要求。以图4（a）所示，添加逆时针驱动，杆件完全进入（或保持在）参考表面的外部，实现了外移动；当选择以图4（b）所示的顺时针驱动方向，杆件完全进入（或保持在）参考表面的内部，实现了内移动。

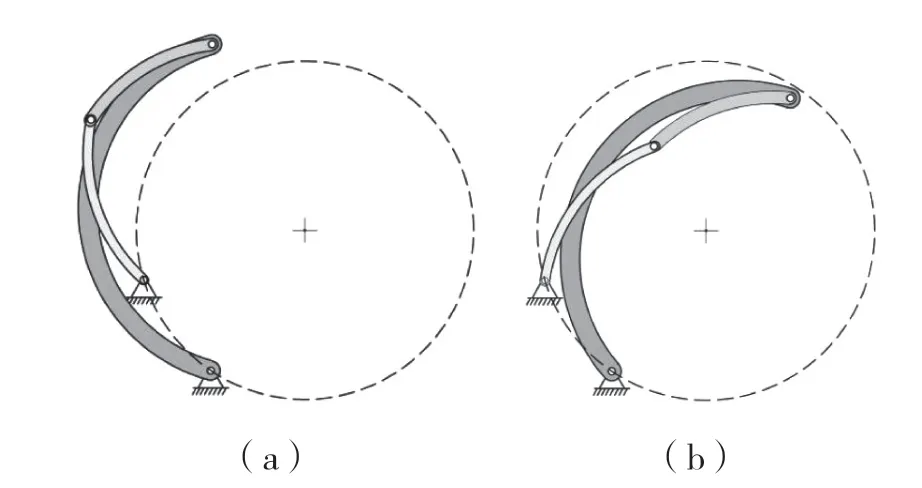
图4 柱面可展机构的移动性Fig.4 Mobility of cylindrical deployable mechanism

3 可展机构分析方法

3.1 瞬时中心参考线法

判断柱面可展机构的运动分类方法有2 种，一种是阴影法，另一种为瞬时中心参考线法。阴影法比瞬时中心参考线法有着明显的局限性，仅能判断机构是否可以完全跨内外移动或者是否不能内移动，所以阴影法并不能具体确定机构运动类型，因此需要瞬时中心参考线法进行具体的可展机构分类。瞬时中心参考线法需要确定瞬时中心参考线ICRL（Instant Center Reference Line）与连杆之间的位置关系，瞬时中心IC（Instant Center）与圆心连线便可得到此连杆对应的瞬时中心参考线。如图5所示，连杆i绕着瞬时中心IC1i旋转，穿过柱型可展曲面的圆心和瞬时中心IC1i的连线就是连杆i对应的瞬时中心参考线ICRLi。

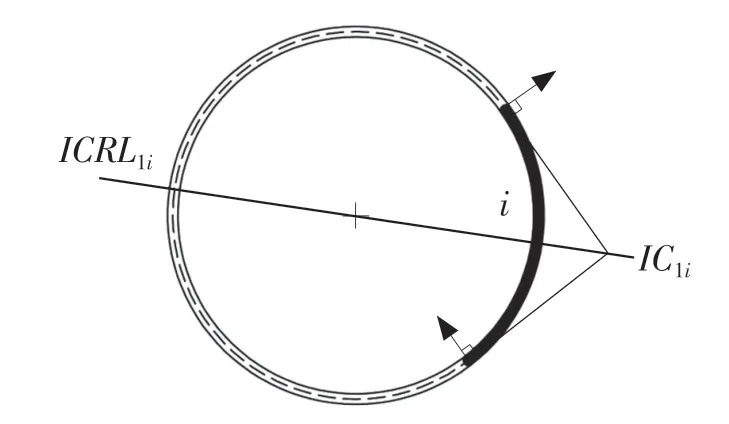
图5 连杆i 的瞬时中心线Fig.5 ICRL of link i

3.2 瞬时中心的确定

瞬时中心参考线法首要步骤是先找到杆件的瞬心，瞬时中心是两个构件在某一时刻没有相对速度的点即零速点[15]。在机构运动分析中，瞬时中心通常用于机构运动的速度分析，并在机构综合中来预测刚体机构中连杆相对运动。瞬时中心的数目可由总构件数计算确定，若机构存在N个构件(包含机架)，则该机构的瞬时中心的总数NIC为

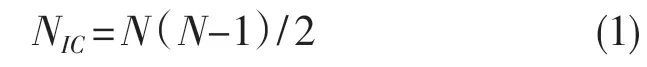
对于直接接触的两构件，利用观察法便可确定瞬时中心；对于不直接接触的两构件，需要利用三心定理确定其瞬心位置。

4 柱面5R 可展机构

4.1 柱面5R 可展机构分析

在柱面可展曲面上选取5 条直母线作为转动副，并满足可展机构的三条准则，从而得到柱面5R 可展机构。利用瞬时中心参考线法的关键在于确定可展机构的瞬心。因为关节轴位于相同位置并且连杆是刚性的，具有直连杆和成形连杆的机构在运动学上是完全等效的，在确定五杆可展机构的瞬心时，通过分析直连杆代替分析成形连杆，这样会更加简单。

根据式（1）可得瞬心总数为10 个。不直接相接触连杆不能通过三心定理来获得所需的瞬心，此时则需通过速度确定杆件的瞬心。应用相对运动图解法求解各构件上各指定点速度，求解时根据速度合成定理列出机构各构件上对应点之间的相对运动矢量方程，并利用一定的比例尺作出矢量多边形，即可得到构件指定点的速度和角速度[16]。无论是阴影法还是瞬时中心参考线法进行机构类型分类，均是利用绘制线图的方式，所以利用相对运动图解法是合理的，其概念清楚，操作分析简单。

如图6 所示，利用直接观察法能确定的瞬心有IC12、IC23、IC34、IC45和IC15，其余瞬心需要利用瞬心定义找到一个未知的瞬心。由于5R 机构为2 个自由度需要2 个驱动，在关节A与关节E处添加一定大小且顺时针方向的角速度ωA和ωE，使得杆2 与杆5 顺时针转动。确定杆1 与杆4 的瞬心IC14便能确定所有的瞬心。由于连杆1 为地，因此确定连杆4 的两端点C与D之间的速度关系就可以确定连杆4 与1 的瞬心。利用相对运动图解法可得式（2）：

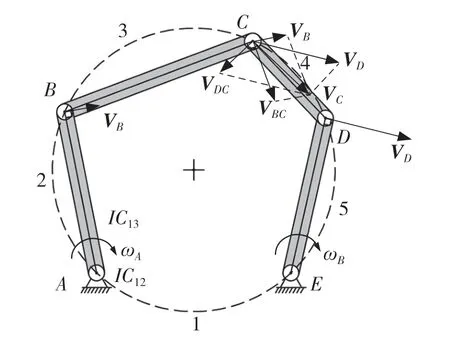
图6 速度合成定理Fig.6 Speed composition theorem

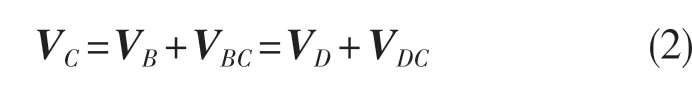
其中，VB、VD的大小方向和VBC、VDC的方向可知，方向均垂直于各自连杆。使用6 个已知量求解剩余2 个未知量VBC和VDC，从而根据速度合成定理确定了VC的大小和方向，得到连杆4 两端点C与D的速度，作VC和VD的垂线，两条垂线的交点即为连杆4 与连杆1 的瞬心IC14。

根据速度合成定理得到瞬心IC14，便可以进一步通过三心定理找到所有的瞬心，瞬心的具体位置如图7 所示。判断连杆相对瞬时中心参考线的位置关系，只需要连杆1 与其余4 个连杆之间的瞬心。将直连杆转换成弧形连杆，用直线将4 个瞬心与参考圆的圆心连接，得到相对应的瞬时中心参考线，如图8 所示。根据连杆i与其对应的瞬时中心参考线IC1i的关系可得，图8 中机构的连杆长度并未超过πR，且未接地的连杆3 对应的瞬时中心参考线ICRL13是未穿过连杆本身的，但未接地的连杆4 对应的瞬时中心参考线ICRL14是完全穿过连杆4 的，因此该机构是属于跨内外运动类型。

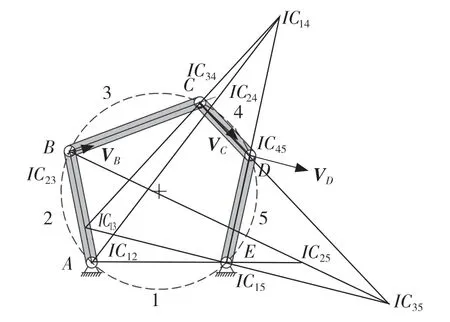
图7 五杆机构的瞬心Fig.7 Instant center of five-bar mechanism

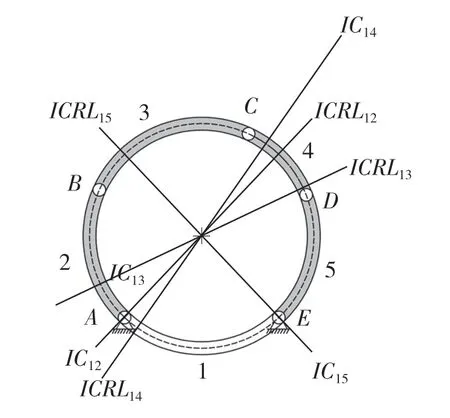
图8 五杆机构的瞬时中心参考线Fig.8 ICRL of five-bar mechanism

由于5R 机构是2 个自由度需要2 个驱动，上述分析是在关节A与E处添加了顺时针方向且大小一定的角速度，在关节A与E还可以添加大小一定但逆时针方向、A顺E逆、A逆E顺的其余3种情况。同理，利用相对运动图解法找到C 点速度，进一步得到瞬心IC14，再根据瞬时中心参考线法得到运动类型。剩余3 种情况中未接地的连杆4 对应的瞬时中心参考线ICRL14都是完全穿过连杆4 的，如图9 所示。未接地的连杆3 对应的瞬时中心参考线ICRL13是否穿过连杆本身不影响判断，都是属于跨内外运动类型。

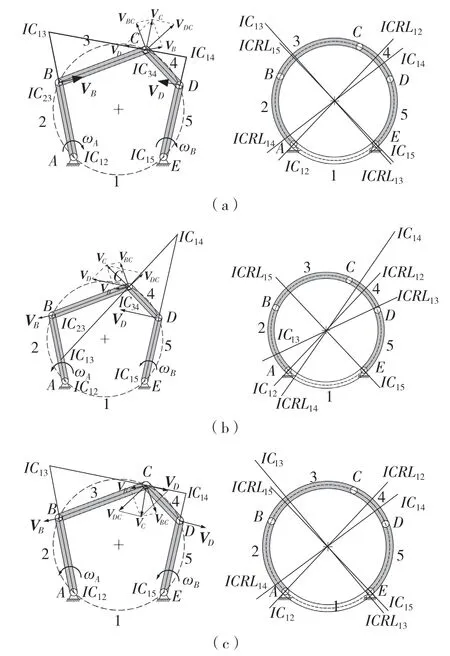
图9 不同驱动情况下的判定Fig.9 Judgment under different drivers

为验证瞬时中心参考线法对二自由度的柱面5R 可展机构运动类型的准确性，可以通过ADAMS软件进行运动仿真，对得到的结果进行验证。

4.2 ADAMS 机构运动仿真

利用SolidWorks 软件建立柱面5R 可展机构的三维模型，并导入到ADAMS 软件中，模型如图10 所示。在2 个固定铰链处添加ωA=30rad/s 和ωE=50rad/s 进行机构运动仿真，仿真过程中改变2个铰链处角速度（不能为0），发现并不会影响固有的运动类型，只有添加的角速度方向才会影响可展机构的运动类型判定，从而可以确定驱动的4 种类型分类的正确性。4 种驱动的情况过程如图11所示。

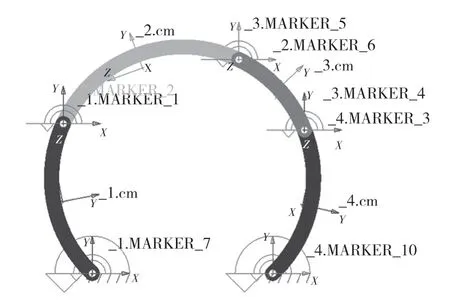
图10 可展机构仿真模型Fig.10 Deployable mechanism simulation model

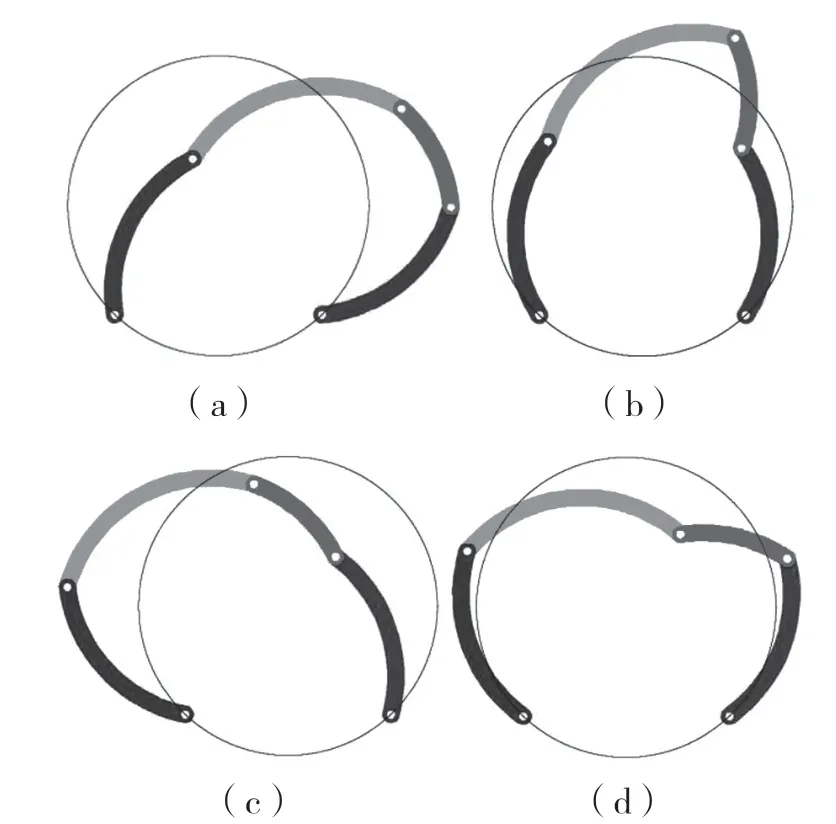
图11 4 种驱动方式运动仿真Fig.11 Four driving modes motion simulation

ADAMS 运动仿真的结果与瞬时中心参考线法判断的结果是一致的，验证了此模型利用瞬时中心参考线法判断运动类型的正确性，文中提出的模型在4 种驱动情形下都为跨内外运动。同时也验证了将相对运动图解法与瞬时中心参考线法相结合分析方法的正确性。

5 结语

本文总结了直纹曲面与可展曲面的基本理论，提出了由单自由度的柱面4R 可展机构到二自由度柱面5R 可展机构的研究。将瞬时中心参考线法结合相对运动图解法推广到了二自由度柱面可展机构的运动类型的判断上，并且分别研究了4 种驱动方向下柱面5R 可展机构运动类型，在可展机构的多自由度研究中奠定了运动分析的基础。通过此种分析方法可以在可展机构设计中预判运动大致位置，减少了直接三维建模设计的错误并提高了效率。若将锥面可展机构进行投影转换，柱面可展机构可拓展到锥面可展机构进行运动分析和位置的预判。