串联电池组接触故障诊断方法研究

李来宝，肖占龙，孙跃东

（200093 上海市 上海理工大学 机械工程学院）

0 引言

锂离子电池单体因电压与容量的限制，所以通常情况下动力电池组由数百节电池单体串并联而成。电动汽车在使用过程中，动力电池组受到安装、振动、腐蚀等一系列因素影响，可能导致电池单体连接处松动，这种松动称之为串联电池组的接触故障[1]。接触故障会使两个电池单体间的接触电阻增大[2-3]，导致连接松动处局部异常产热，加快电池老化，减少其剩余循环寿命，加剧电池组的不一致性[4]，接触故障严重时可能会造成电池热失控事故。由于存在接触电阻，电压测量误差有很强的不确定性与随机性，导致电池组状态估计出现严重偏差[5]。而且电池组内单体数目较多，逐个排查维修困难巨大[6]。因此，实时诊断电池组接触故障并定位故障单体，对保障动力电池组安全运行具有重要意义[7]。

为解决以上问题，本文提出一种基于自适应白噪声的完整经验模态分解（CEEMDAN）和模糊熵的串联电池组接触故障诊断的算法。该算法的核心思想是通过CEEMDAN 方法提取接触故障特征信号，然后计算模糊熵来实时诊断，并通过仿真与实验验证了该算法对电池组接触故障进行诊断和定位的准确性。

1 基本原理

1.1 CEEMDAN 方法

CEEMDAN 方法主要用于非平稳和非线性信号的时域分析，该算法通过添加自适应的白噪声并计算信号余量来分解得到一系列IMF，弥补了EEMD和EMD 算法信号重叠和计算效率低的问题。

CEEMDAN 的分解步骤如下：

（1）对任意时间序列的电压信号U（t）可表示为

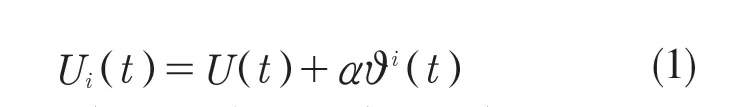
式中：α——添加的白噪声的标准差；ϑi（t）,i=1,…,N——满足标准正态分布的高斯白噪声N（0,1）。

（2）对每个Ui（t）进行EMD 分解，得到第1个模态分量：

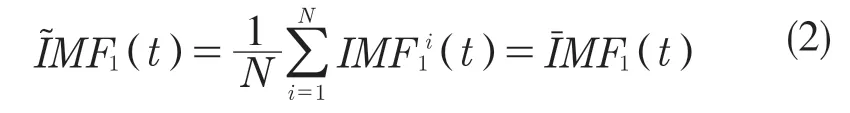
（3）在m=1 时，计算第1 个信号余量：

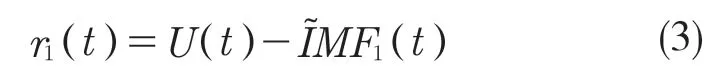
（4）分解信号r1+α1E1（ϑi（t））,i=1,…,N直到得到第1 个模态分量，然后计算下一个模态分量：

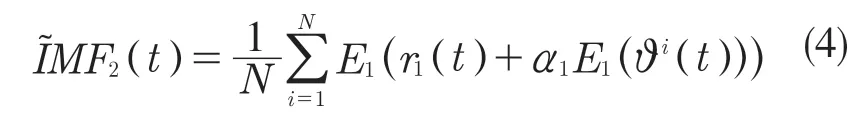
（5）对m=2，…，M，计算第m次信号余量：

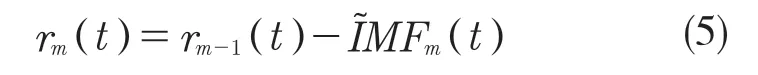
（6）分解信号rm+αm Em（ϑi（t））,i=1,…,N直到得到第1 个模态分量，并定义第m+1 个分量：

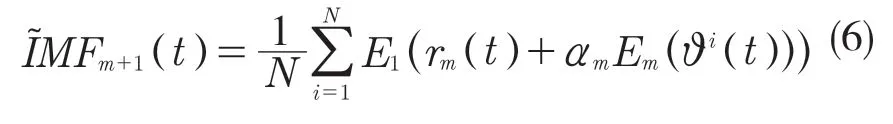
（7）重复步骤（4）—步骤（6），直到信号余量的极值点不超过2 个停止分解。最终的信号余量为

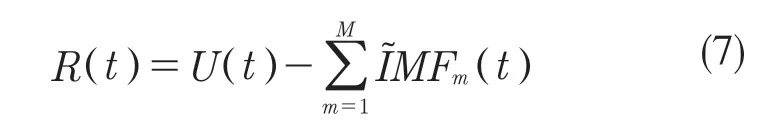
式（7）中，m为分解总模式数。则原始信号U（t）可表示为

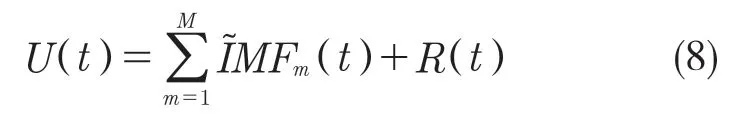
1.2 CEEMDAN 的应用

为了验证本文提出的CEEMDAN 方法在电池电压信号中的有效性，基于如图1 所示的新欧洲驾驶循环（NEDC）工况对锂离子电池单体进行测试，测试开始时电池单体为100%SOC 状态。电池的基本性能参数如表1 所示。

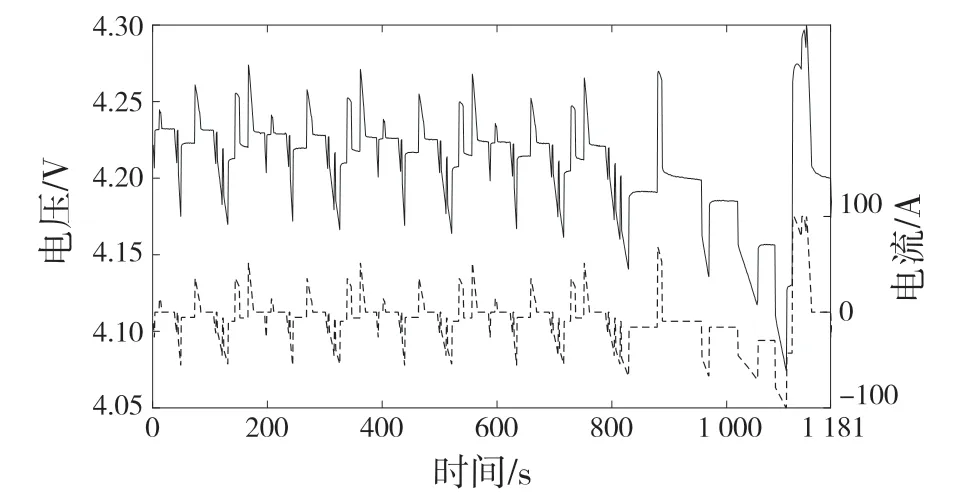
图1 NEDC 工况下电池的端电压和电流Fig.1 Terminal voltage and discharge current of battery under NEDC conditions

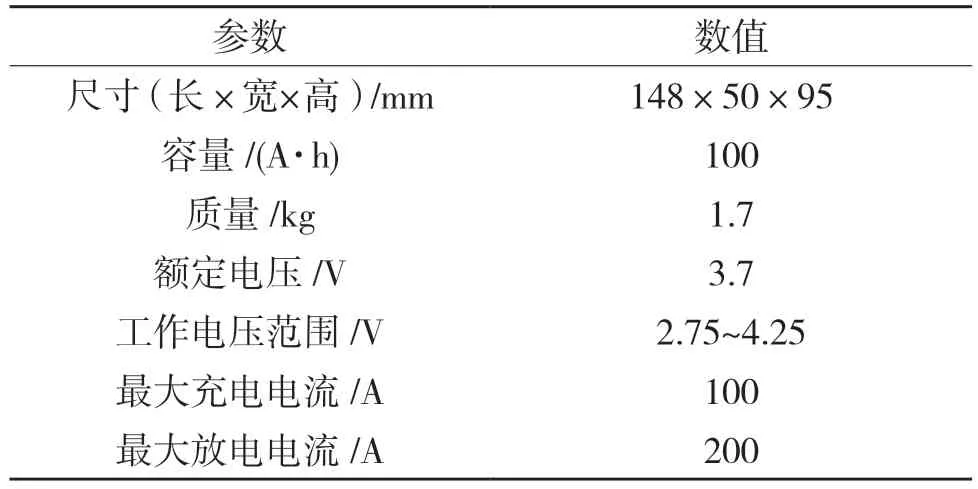
表1 锂离子电池基本性能参数Tab.1 Basic performance parameters of lithium-ion battery

如图2 所示，采用上述CEEMDAN 方法将原始端电压信号分解为10 个IMF 动态分量和1 个稳态信号余量，其中IMF1 至IMF10 从高频到低频依次排列。可以看出，IMF1 至IMF10 不仅可以表现电压动态波动情况，还可以捕捉电池运行过程中的故障特征，而稳态信号余量则不受电压动态波动的影响，只表现电池稳态变化的情况。因此在本文中，为了检测串联电池组接触故障，采用除稳态信号余量以外的所有动态分量之和作为故障特征信号。

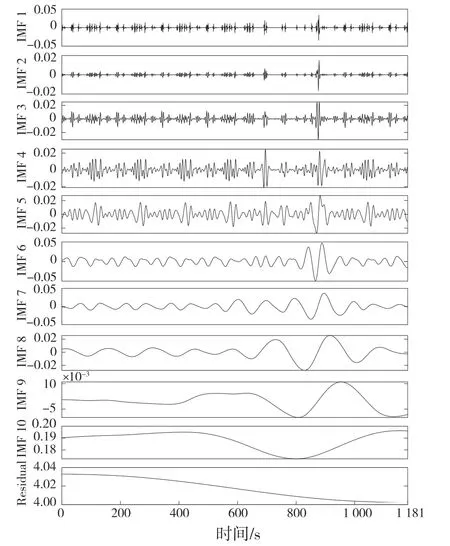
图2 端电压信号的CEEMDAN 分解结果Fig.2 CEEMDAN decomposition result of terminal voltage signal

1.3 模糊熵理论

熵的概念首先由香农提出，并已成功应用于测量和评估信息科学和热力学的不确定度。在一定条件下，系统越无序，即不确定性越高，系统的熵值越大；反之，熵值越小。

对于长度为N的时间序列电压信号U（t）,其模糊熵的定义如下：

（1）定义m维和m+1 维向量分别为

式（9）、式（10）中：i=1，2，…，N-m；um（i），um+1（i）——m维和m+1 维向量的平均值。

（2）定义2个向量Uim（Uim+1）和Ujm（Ujm+1）表示相应元素之间的差异，其最大差值dijm（dijm+1）为2 个向量之间的距离，即

式（11）、式（12）中：i，j=1，2，…，N-m，i≠j。

（3）定义模糊函数η（dijm，n，r），确定向量之间的相似度，即

式（13）、式（14）中：n——边界梯度；r——宽度。

（4）定义函数

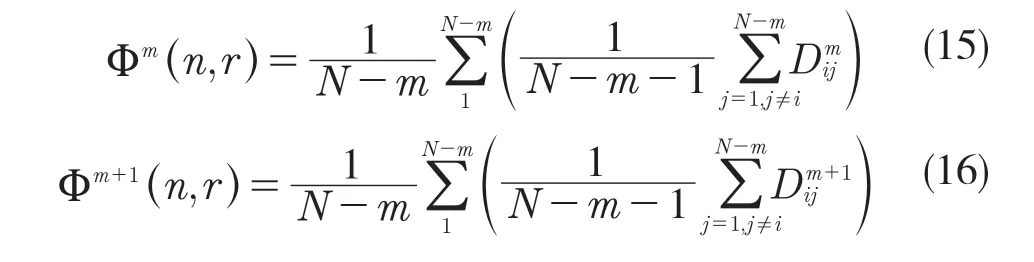
（5）当时间序列电压信号U（t）为有限长度时，其模糊熵可定义为

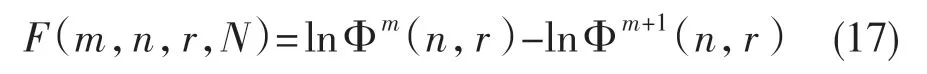
在本文中，为了提高算法的实时性与灵敏度，引入了移动窗口作为数据实时更新机制。移动窗口的大小W实际上是指用于计算一个模糊熵的数据个数。模糊熵的计算精度受数据个数的影响,一般来说，计算一次模糊熵的数据越多，其精度越高，然而这也意味着会占用更多的内存，花费更长的时间。因此，W的选择是计算精度、内存占用和计算速度之间的平衡。通过多次数据试验分析，本文选取W=50。另外，本研究中取m=2，n=2，r=0.15Std（Std 为标准差）。

1.4 故障诊断方法

通过对CEEMDAN 方法和模糊熵理论的研究，再根据接触故障单体端电压信号特点，得到基于CEEMDAN 和模糊熵的串联电池组接触故障诊断算法。如图3 所示，该算法主要由CEEMDAN 分解、动态分量提取、模糊熵计算、故障识别4 个部分组成。在故障识别部分，根据计算得到的各单体模糊熵值，定义故障识别参数：

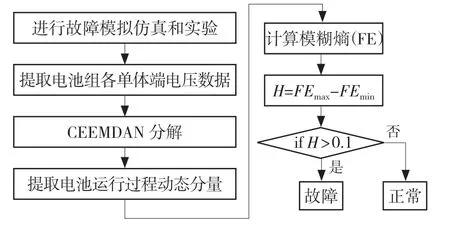
图3 接触故障诊断方法Fig.3 Contact fault diagnosis method

式中：FEmax——模糊熵的最大值；FEmin——模糊熵的最小值。当H＞0.1 时，则诊断为电池组存在接触故障，反之则正常。

2 仿真与实验结果分析

2.1 仿真及结果分析

基于Simulink 搭建6 节单体串联的电池组模型，各电池单体的基本性能参数如表1 所示。为了模拟电池组接触故障，在仿真过程中给单体6 串联一个接触电阻Rc。汽车行驶过程中由于受到振动、冲击等，会使接触电阻Rc发生跳变，因此Rc设置为0.5～5.0 mΩ，随机变化频率为0.5 Hz。采用新欧洲驾驶循环（NEDC）工况进行仿真，采样频率为1 Hz，仿真电压结果如图4 所示。从图4（a）中可以看出，在相同的动态工况下，由于单体6 存在可变接触电阻故障，其电压比正常单体变化范围更大且无规律。具体如图4（b）所示，在第278 s、290 s，故障单体6 与正常单体最大电压差分别达到-500 mV、250 mV,而正常单体之间的电压差仅为10 mV 左右。

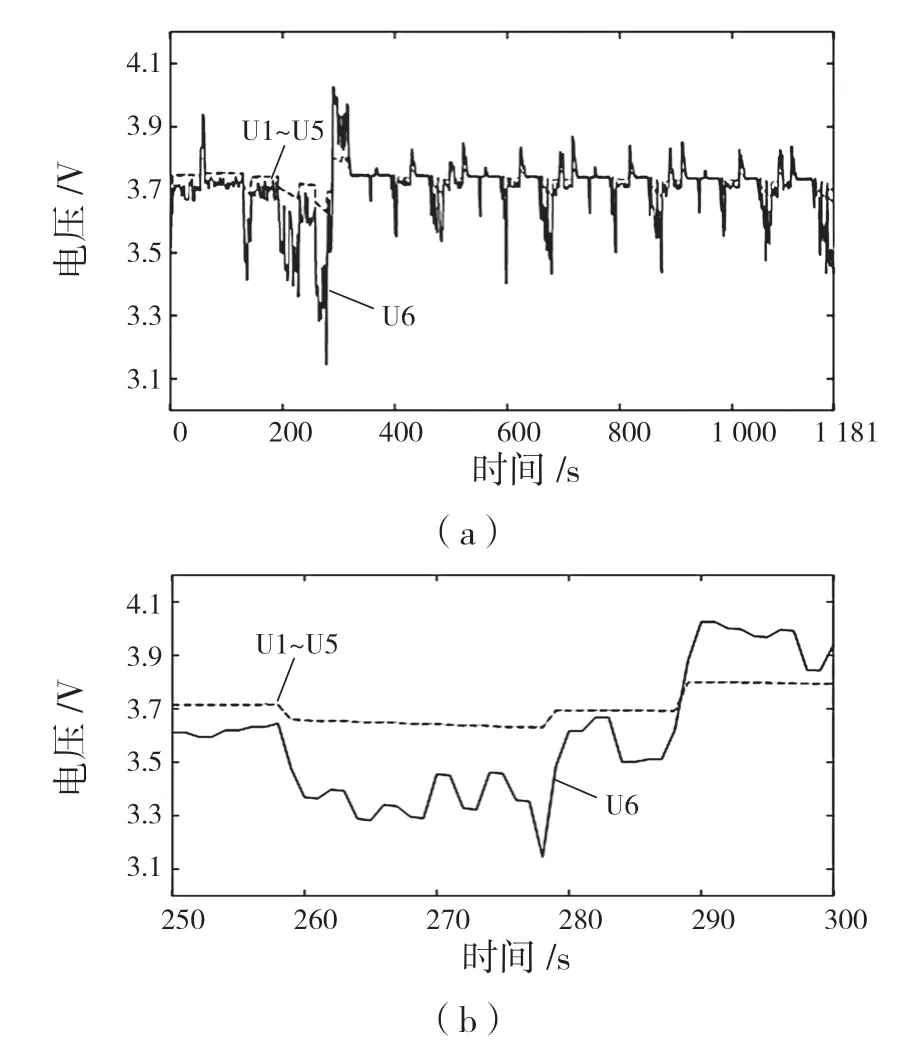
图4 带有接触故障的仿真电压结果Fig.4 Simulation voltage results with contact failure

使用本文提出的算法计算电池组内各单体端电压信号的模糊熵值，结果如图5 所示。可以看出，在整个运行过程中，由于单体6 存在接触故障，端电压波动异常，其端电压的模糊熵值在0～0.26 范围内剧烈波动，而其余5 个单体端电压的模糊熵最大值仅为0.05 左右。基于图5 所示的模糊熵值，再结合式（18），得到如图6 所示整个测试过程的故障识别结果。值得注意的是，在此过程中多次触发故障报警，表明该算法有较好的稳定性，可以持续检出电池组中的接触故障。

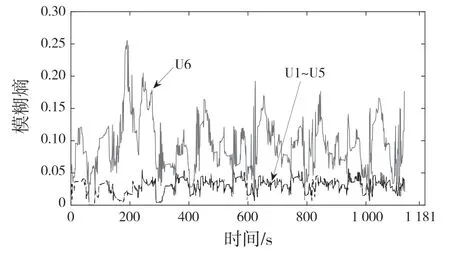
图5 仿真数据模糊熵计算结果Fig.5 Fuzzy entropy calculation results of simulation data

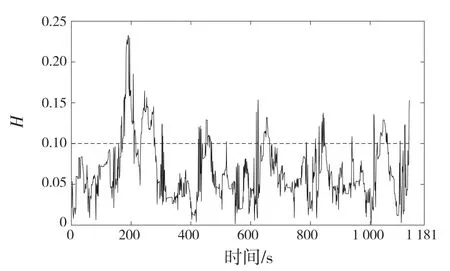
图6 故障识别结果Fig.6 Fault identification result

2.2 实验及结果分析

实验平台如图7 所示。使用新威CT-4000 电池测试台架进行电池的充放电控制，台架的电压采集精度为1 mV，采集频率为1 Hz，并通过CAN 通讯将数据传输至上位机。实验选用模组内部包含6个串联的电池单体，额定容量为100 A·h，电池单体的基本性能参数同表1。实验开始前调整各单体SOC 一致。为了模拟串联电池组接触故障，本实验采取在电池模组外接一个同型号电池单体，并在模组和单体间串联3.3 mΩ 定值电阻的方案，电压采样时将外接单体作为单体1，模组内取5 个单体组成新的6 串模组。实验工况与仿真工况保持一致，均采用新欧洲驾驶循环（NEDC）动态工况。由于实验具有一定的危险性，所以全程在防爆箱中进行。

图7 串联电池组实验平台Fig.7 Series battery pack experiment platform

图8 为某次NEDC 循环工况下各单体电压。可以看到单体1 的电压波动范围更大。当电流大于零时，单体1 的电压高于其他正常单体，且最大压差为580 mV 左右；当电流＜0 时，单体1 的电压低于其他正常单体，且最大压差为-700 mV 左右。这与仿真电压结果趋势是一致的。

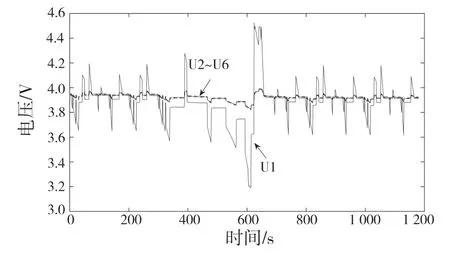
图8 带有接触故障的实验电压结果Fig.8 Test voltage results with contact failure

图9 为实验数据模糊熵计算结果。从图中可以看出，单体1 的模糊熵值波动剧烈且与另外5 个单体有较大差异。图10 为故障识别结果，在实验过程中多次触发接触故障报警，并且在算法刚开始迭代H就高于故障阈值，表明算法具有良好的实时性与灵敏度。

图9 实验数据模糊熵计算结果Fig.9 Fuzzy entropy calculation results of test data

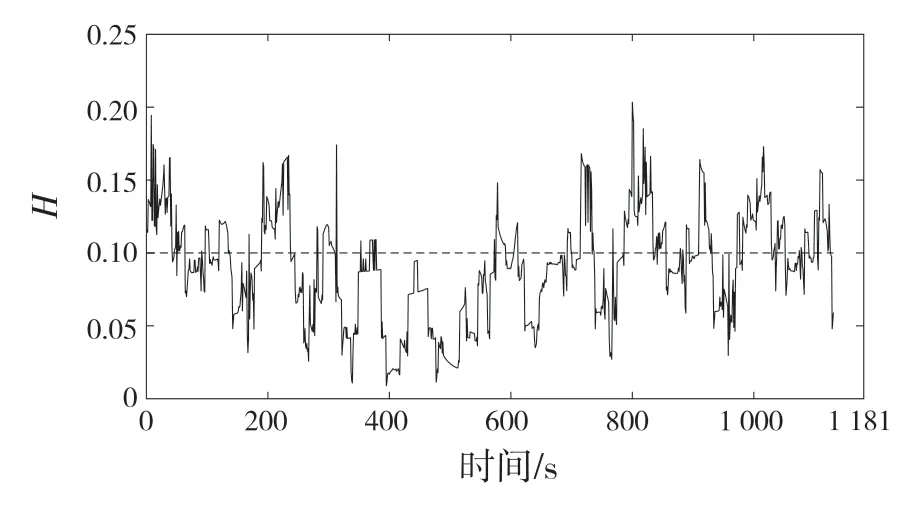
图10 故障识别结果Fig.10 Fault identification results

3 结论

本文对串联电池组接触故障诊断进行了研究，提出了一种基于CEEMDAN 和模糊熵的接触故障诊断方法。首先，根据电池的动态放电数据，利用CEEMDAN 方法分解获得一系列的IMF 和一个信号余量，其次，通过故障特征提取方法获得电池运行过程的动态分量，然后，根据带移动窗口的模糊熵算法计算每个单体的模糊熵。最后，通过分析电池单体历史模糊熵变化特征，并结合所设阈值进行接触故障诊断。仿真与实验结果表明，本文提出的接触故障诊断方法可准确诊断并定位故障单体，对提高新能源汽车电池管理系统故障诊断的实时性与稳定性有较大作用。