基于AMESim-Simulink 的电液位置伺服系统的自适应模糊PID 控制

余长顺，袁锐波

（650093 云南省 昆明市 昆明理工大学 机电工程学院）

0 引言

液压伺服系统特别是电液伺服系统以其响应快、精度高、功率大、系统刚度大等特点被广泛应用于工业各领域。但电液伺服系统是一种非线性时变系统，它存在的死区、参数变化、外负载干扰等问题严重影响伺服系统的控制性能[1]。常规PID 控制选取合适的PID 参数，对线性时不变系统具有良好的控制性能，被广泛应用于工业控制场合。但是PID 控制需要建立精确的数学模型，对于复杂的非线性控制系统，很难取得较好的控制效果。而模糊控制不需要系统变量的精确数学模型，鲁棒性较好，但是其本身消除系统稳态误差的能力比较差[2-4]。

为了既实现控制器参数自动调整又能提高消除系统稳态误差的能力，本文将通过AMESim/Simulink 软件平台，在AMESim 中建立电液位置伺服系统的物理系统模型，在MATLAB 中采用综合PID 控制和模糊控制的自适应模糊PID 算法，并将其用于电液位置伺服系统的控制系统设计，仿真实验研究表明，该方法具有良好的控制跟踪性能。

1 电液位置伺服系统

系统工作原理如图1 所示。系统由恒压油源供给压力油，通过位移传感器测得的液压缸位移值与给定值作差，控制器由此差值控制电液伺服阀阀口开度，也即进出液压缸的流量，从而控制液压缸的位移。

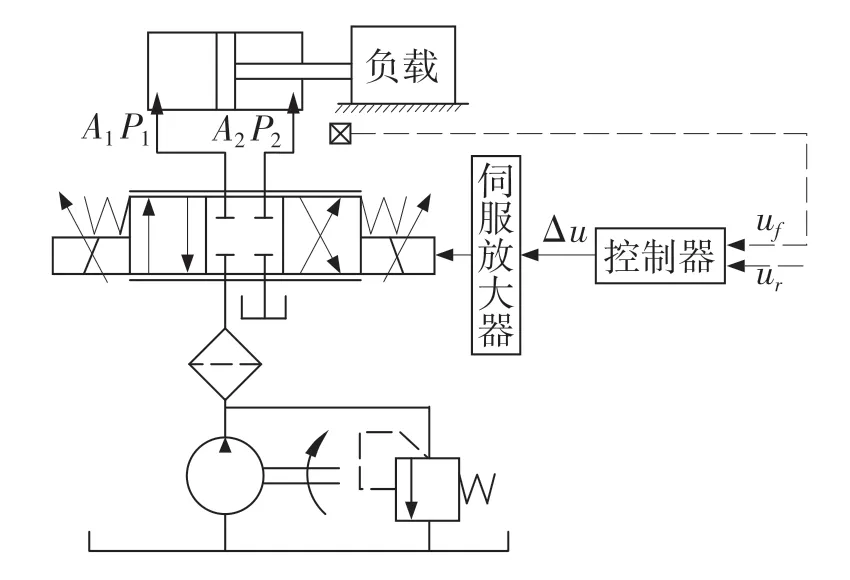
图1 电液位置伺服系统原理图Fig.1 Schematic diagram of electro-hydraulic position servo system

由电液位置伺服系统原理建立其数学模型，首先要进行各环节的传递函数推导。

1.1 电液伺服阀数学模型

电液伺服阀包括伺服阀和伺服放大器，伺服放大器通常可近似为比例环节，其传递函数为

式中：Ka——伺服阀放大系数；Δu——输入信号ur与反馈信号uf的差值。

大多数伺服系统的电液伺服阀可采用2 阶振荡环节的形式，其传递函数为

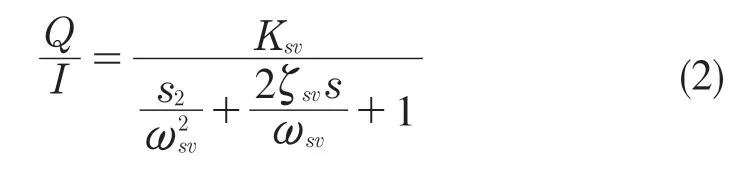
式中：Q——伺服阀输出流量；ωsv——伺服阀固有频率；Ksv——伺服阀放大系数；ζsv——伺服阀阻尼比。

1.2 液压缸及负载数学模型

当系统弹性负载K=0 时，可得阀控非对称液压缸的传递函数为

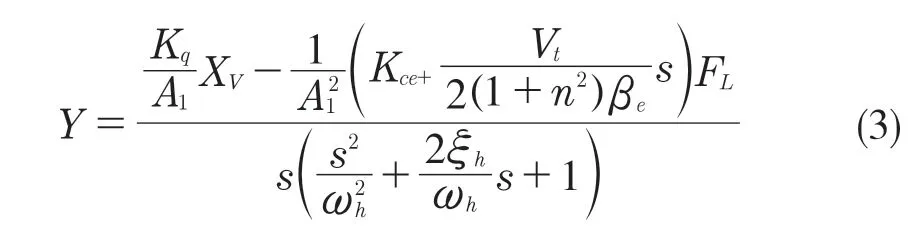
式中：Kq——滑阀流量增益；xv——活塞位移；Kce——总流量压力系数；FL——外负载；A1——液压缸进油腔面积；ωh——液压固有频率；ξh——液压阻尼比；n——液压缸左右两腔有效面积比；Vt——液压缸两腔的总容积；βe——油液的等效体积弹性模量。

1.3 电液位置伺服系统开环传递函数

根据经典控制理论，在阀控非对称缸空载情况下，电液位置伺服系统的开环传递函数为

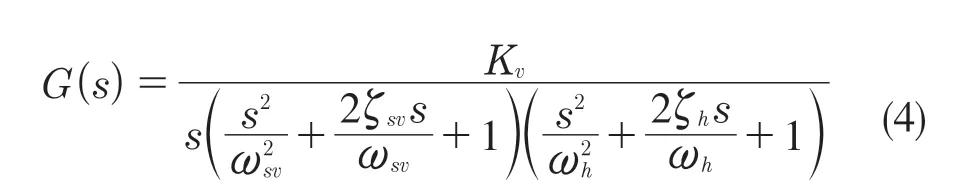
式中：Kv——系统开环放大系数，Kv=Ka Ksv Kf/A1。

2 模糊自适应PID 控制器设计

2.1 自适应模糊PID 控制器结构

本文将常规PID 控制与模糊控制相结合，设计了自适应模糊PID 控制器，在常规PID 控制器的基础上增加了一个模糊推理模块，模块采用两输入三输出结构。输入为系统输出与控制量之间的误差信号e（t）和误差信号的微分de/dt，输出为PID 控制器的增益系数kp、ki和kd，通过式（5）对PID 控制器的参数kp、ki和kd进行自适应整定,使被控对象保持在良好的动、静态稳定状态[5-6]。自适应模糊PID 控制器的结构如图2 所示。

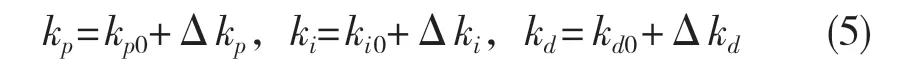
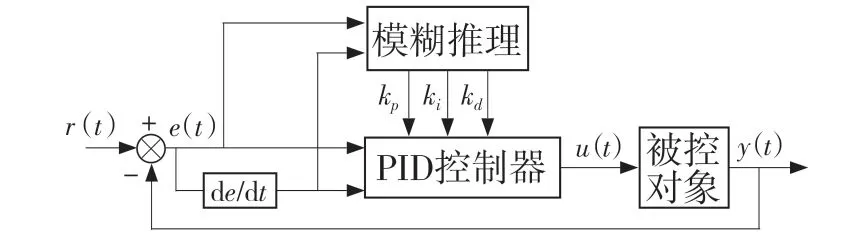
图2 自适应模糊PID 控制结构图Fig.2 Adaptive fuzzy PID control structure diagram

2.2 输入、输出变量及其隶属度函数设定

本文设置模糊控制器为两输入三输出方式，推理方式选用Mamdani 型。本文中e，de/dt，kp，ki，kd的隶属函数均采用三角形隶属度函数。分别分为7 个模糊集语言变量：“负大（NB）”，“负中（NM）”，“负小（NS）”，“零（ZO）”，“正小（PS）”，“正中（PM）”，“正大（PB）”，论域范围均采用Mamdani 的模糊量化方法，将其离散为{-6，-4，-2，0，2，4，6}。误差e和误差变化率de/dt的取值用隶属函数表示，如图3 所示。

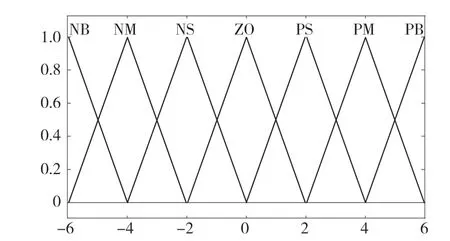
图3 误差e 和误差变化率de/dt 三角形隶属度函数Fig.3 Fuzzy membership functions of e and de/dt

2.3 模糊控制规则表设计

根据专家经验[7]，设定模糊参数kp、ki、kd的规则表如表1 所示。

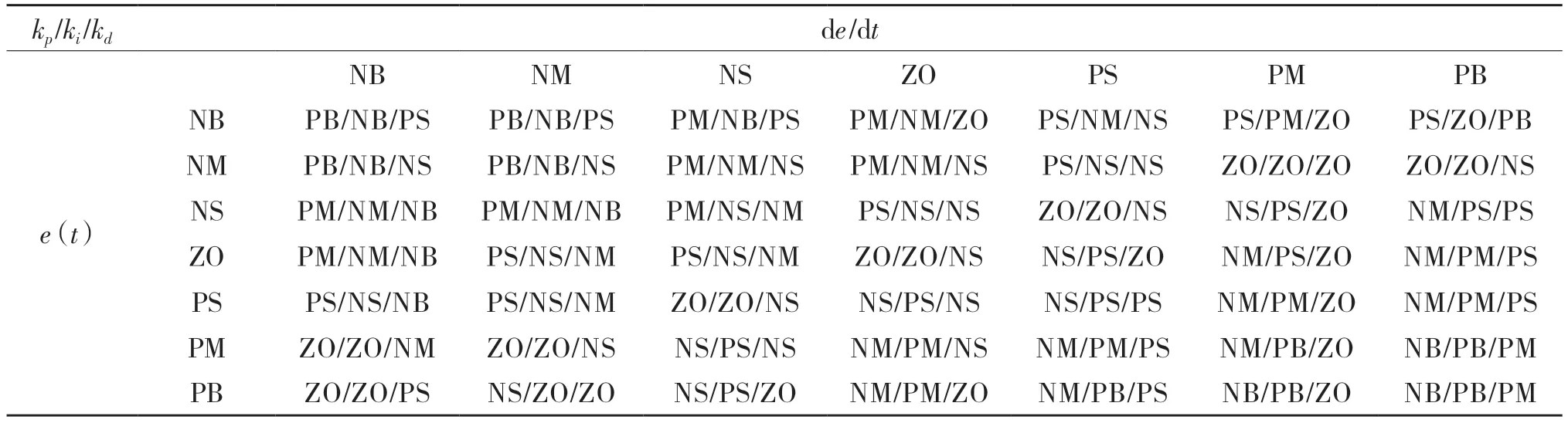
表1 模糊参数kp/ki/kd 控制表Tab.1 Fuzzy parameter kp/ki/kd control

2.4 解模糊

反模糊化主要有最大隶属度法、重心法和加权平均法3 种。为了获得较为准确的控制量，本文选用面积重心法。在完成模糊控制器的设计后，通过plotfis（fuzzypid002）命令，可以得到模糊控制器fuzzypid002 的结构图如图4 所示。

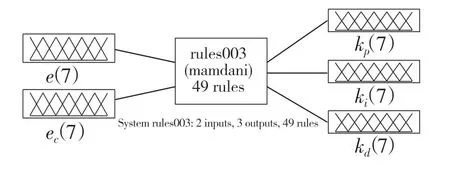
图4 模糊控制器fuzzypid002 的结构图Fig.4 Structure diagram of fuzzy controller fuzzypid002

3 系统建模与仿真分析

3.1 仿真方法

本文在AMESim 中搭建电液位置伺服系统的物理建模，在Simulink 软件中搭建系统的控制模型。通过创建联合仿真接口来实现两个软件之间数据交换，其流程为：接口模块将位移传感器测得的液压缸位移信号作为输入传送到MATLAB 中，再将MATLAB 的输出信号作为控制信号来控制伺服阀的开度，从而控制液压缸的位置，由此形成闭环控制。

3.2 AMESim 中系统物理模型搭建及参数设置

为了观察模糊PID 控制算法对于电液位置伺服系统的控制效果，本文在AMESim 中搭建好电液位置伺服系统的物理模型，并根据实际设置其参数，创建了AEMSim 与Simulink 之间用以交换数据的接口模块。所建立的模型如图5 所示。

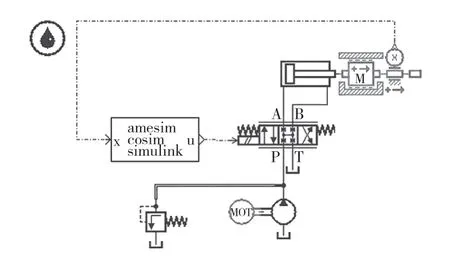
图5 电液位置伺服系统AMESim 模型Fig.5 AMESim model of electro-hydraulic position servo system

系统主要参数设定如下：液压缸缸径32 mm，活塞杆直径16 mm，液压缸行程1 m；电机转速为1 500 r/min；泵的转速为1 500 r/min，排量为20 mL/r；溢流阀调整压力设置为30 MPa；电液伺服阀固有频率设置为80 Hz，额定电流为1 000 mA，将其各通路的流量设置为3 MPa 压差下，最大开度40 L/min；负载总质量为100 kg；位移传感器的增益为1。其他参数设置为默认值。

3.3 搭建Simulink 控制模型

在Simulink 中搭建电液位置伺服系统的控制模型，其中模糊自适应控制律的编写由S 函数完成。S 函数为6 输入1 输出，整个模糊控制采用49 条规则。可以通过转换开关选择阶跃输入或正弦信号输入，整个控制系统模型如图6 所示。

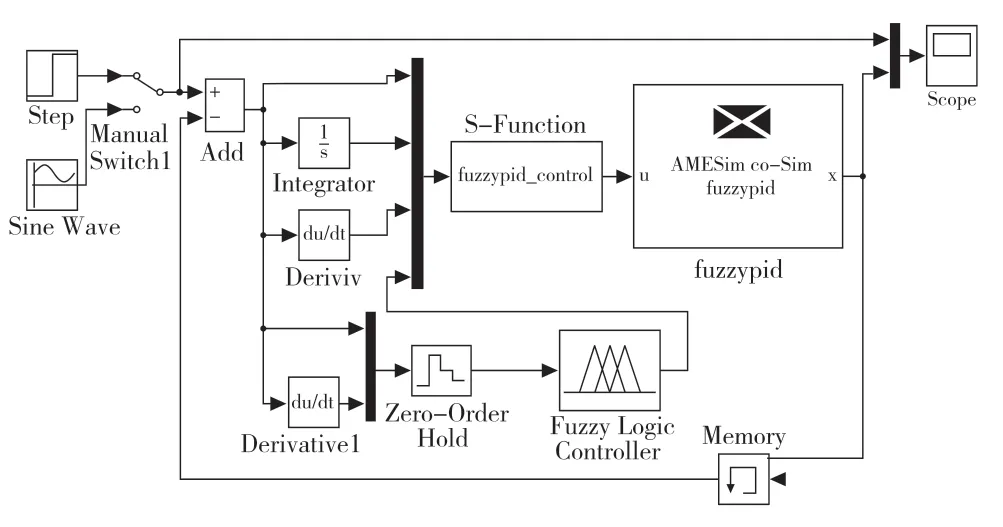
图6 Simulink 控制仿真模型Fig.6 Simulink control simulation model

3.4 仿真验证及结果分析

基于图5 和图6 的模型进行系统的AMESim-Simulink 的联合仿真，通过试凑法得到初始的PID控制参数。给定系统以阶跃和正弦2 种输入信号观察其输出响应。分别设置阶跃信号的幅值为0.5 m，阶跃时间为1 s，正弦信号的输入幅值为0.2 m，偏置为0.2。运行Simulink 进行系统仿真，可得系统的模糊PID 阶跃输入和正弦输入跟踪响应曲线分别如图7 和图8 所示。

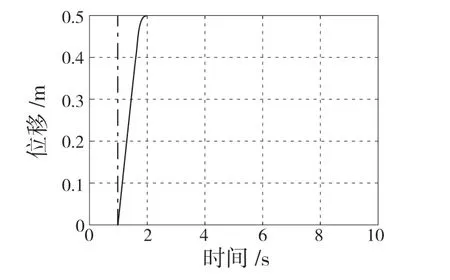
图7 自适应模糊PID 阶跃输入响应图Fig.7 Step input response diagram of adaptive fuzzy PID

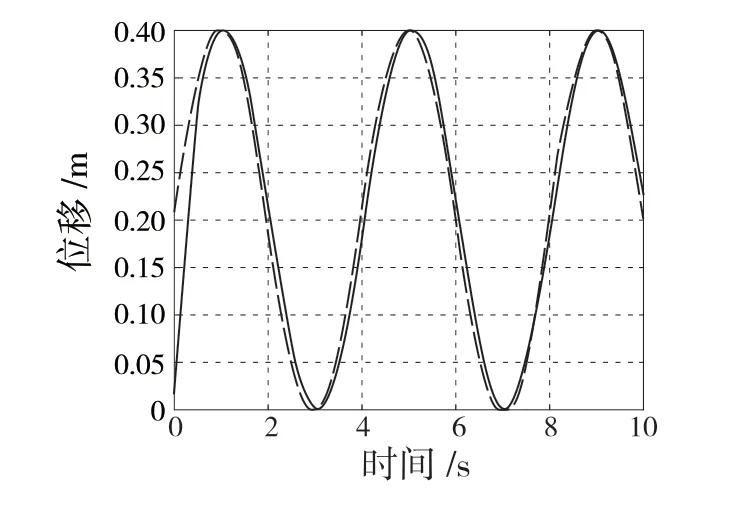
图8 自适应模糊PID 正弦输入响应图Fig.8 Sine input response diagram of adaptive fuzzy PID

可以看出：系统的阶跃响应在2 s 前达到稳态，响应迅速，系统无超调；而系统的正弦响应在1 s内很快跟踪到输入信号且跟踪精度良好。通过系统的阶跃响应和正弦响应可以看出，自适应模糊PID控制算法对于电液位置伺服系统具有良好的跟踪控制特性。

4 结论

本文对电液位置伺服系统进行了建模分析，设计出自适应模糊PID 控制器，通过搭建电液位置伺服系统的AEMSim-Simulink 的仿真平台，给定不同的输入信号，得到自适应模糊PID 控制对于不同输入下的跟踪特性。仿真结果表明:自适应模糊PID 控制器对于输入信号具有控制响应速度快、无滞后和超调、跟踪精度高等特性，取得了较好的控制效果。