滑枕动态性能分析与试验验证

杨 军， 廖广宇， 王 丹， 邱海莲

（云南省机械研究设计院有限公司 云南省机电一体化应用技术重点实验室， 云南 昆明 650031）

0 引言

滑枕是机床的主要功能部件， 其结构的动态性能直接决定着机床的加工精度，因此，在设计阶段就必须对其动态性能进行准确的预估。滑枕是我公司与企业合作，针对市场需求研发的龙门数控铣床的功能部件， 该机床主传动系统为齿轮变速、结构复杂，装配在滑枕内。因此，准确预估滑枕动态性能成为其设计、开发是否成功的关键。利用计算模态与试验模态结果，通过相关性分析，准确预测滑枕的动态特性。

1 机械动力学分析概述

机械动力学分析是基于已有机械的动力学模型、系统工作条件和外部激励等因素，分析机械系统动态特性，包括固有频率、动力响应及稳定性等。 目前，机械结构动力学分析方法主要有三类：①有限元建模及分析；②试验建模及分析；③有限元分析与试验相结合。 本文采用有限元分析与试验相结合的方法对滑枕动态特性进行仿真分析与试验研究，将仿真模态与试验模态进行对比分析，以验证仿真模态分析的准确性， 为结构动态性能优化奠定基础。

2 滑枕动态特性有限元分析

2.1 材料属性定义

滑枕采用HT300 材料，整体浇铸成型、并进行时效处理。 其材料参数见表1。

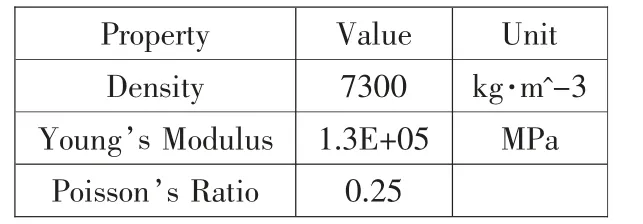
表1 材料参数定义

2.2 滑枕模型建立

利用Solidworks三维设计软件完成滑枕的实体建模，对螺纹安装孔系、小型倒角等简化三维模型，见图1；应用Patran Nastran 作为CAE 分析软件，对滑枕划分网格大小为20mm 的四面体网格， 并对滑枕进行有限元分析，见图2。

图1 简化后的滑枕模型

图2 滑枕划分四面体网格

2.3 滑枕模态分析

分析中采用自由边界条件，进行求解分析；经过有限元分析计算，得到滑枕的6 阶固有频率及相应的振型。见表2。

表2 滑枕固有频率及振型

3 滑枕试验模态分析

在机械结构动力学分析中， 试验模态分析技术主要用于测定结构的3 个基本参数：结构的固有频率、阻尼比和模态振型。 根据试验模态分析技术所得到的基本参数可以显示结构的固有特性， 通过对比试验模态测试结果与有限元分析结果，可以检验有限元模型是否准确。另外通过结构的试验模态分析，观察振型的振幅情况，可以获得结构的薄弱部件， 从而为结构的动态结构优化设计提供必要的参考依据。

3.1 模态试验系统

采用B&K8207 力锤进行激振，力锤频率范围0～1000Hz，灵敏度0.225mV/N， 最大激励力5000N；B&K4506B 三向加速度传感器获得响应信号， 传感器频率范围：0.6～3000Hz，灵敏度为100mV/g，测量范围（峰值）70g，最大冲击（峰值）5000g；使用B&K 3660C 数据采集前端与B&K基本分析系统以及PULSE Reflex 高级模态采集与分析包，构成试验测试分析系统，见图3。

图3 试验模态测试原理图

3.2 模态测试

测试采用软绳吊装， 将滑枕悬空吊装模拟其自由边界进行试验，见图4。

图4 模拟滑枕自由边界条件

使用锤击法， 激励点为滑枕导轨靠主轴端的X向、Y 向、Z 向， 测量方式为固定参考点， 移动传感器方法。 本试验整个滑枕共布置380 个测点， 响应自由度为380×3=1140。 激励点依据工程经验选择在滑枕导轨靠主轴端， 数量为1 个， 激励自由度为3个正交方向，总FRF=1140×3=3420，见图5。

图5 测量响应自由度

分析带宽设为1.6KHz，谱线数设为1600，频率分辨率为1Hz，平均方式为线性平均，平均次数为5 次；激振力大小为1.0KN～1.5KN； 对力锤脉冲信号使用Transient窗函数，对响应信号使用Exponential 窗函数；滤波器设为7Hz 高通滤波，FRF 为自动量程采集。

3.3 测试结果

使用PULSE Reflex 分析软件， 选择分析带宽为0～600Hz；采用多参考最小二乘复频域法结合复模态指数函数 （CMIF） 和稳态图识别模态参数， 利用模态判定准则（MAC） 对得到的模态结果进行验证，进而得到频率区间内滑枕各阶固有频率和阻尼比，见表3。

表3 滑枕前6 阶固有频率和阻尼比

3.4 测试结果分析

通过对滑枕进行模态测试，得到其低阶模态参数与振型。 在低阶振型中，主轴变速箱体部分采用四边形结构，在箱体顶部和箱体内部主传动齿轮的轴承座板处存在局部弯曲和扭摆， 振幅较大，建议进一步改进、以提高结构的刚度。

4 试验模态模型与有限元模型相关性分析

为对比结构动力学仿真与试验模态的相关性分析，确定计算分析结果和试验分析结果的对应关系。 通常需要用到一系列方法对试验数据与仿真数据进行对比，包括：频率、振型等相关性分析。

4.1 频率相关性分析

滑枕前6 阶固有频率有限元计算结果与试验测量结果对比情况见表4。 可知：有限元计算所得的各阶固有频率与试验测得的频率值的相对误差的绝对值最大约为1.60%。

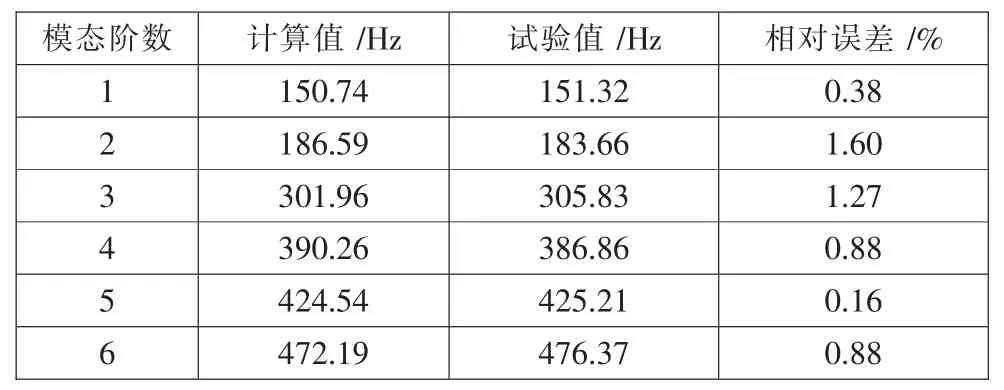
表4 固有频率的相对误差

4.2 振型相关性分析

对模态振型进行比较的目的之一是进行模态匹配，主要对其变形位置、 振型方向等相关信息的一致性进行分析比较。

（1）1 阶振型：图6 为滑枕第1 阶模态振型，部件1 次左右扭摆动作。

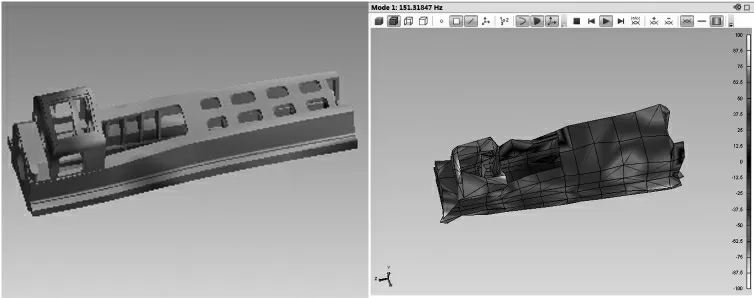
图6 1 阶模态振型

（2）2 阶振型：图7 为滑枕第2 阶模态振型，部件1 次上下弯曲动作。

图7 2 阶模态振型

（3）3 阶振型：图8 为滑枕第3 阶模态振型，部件1 次左右弯曲动作。

图8 3 阶模态振型

（4）4 阶振型：图9 为滑枕第4 阶模态振型，部件2 次上下弯曲动作。

图9 4 阶模态振型

（5）5 阶振型：图10 为滑枕第5 阶模态振型，部件2次左右扭摆动作。

图10 5 阶模态振型

（6）6 阶振型：图11 为滑枕第6 阶模态振型，部件头部左右扭摆，尾部上下弯曲。

图11 6 阶模态振型

4.3 相关性分析结果

滑枕固有频率的相对误差的绝对值最大约为1.60%，振型的变形位置、向量方向一致。 结果表明：计算模态中参数设置合理、试验模态的设计与测试正确。

5 结束语

本试验对滑枕部件分别进行了有限元分析和试验模态测试，并进行了二者的相关性分析；获得了滑枕的特征参数，验证了滑枕动态分析的正确性，为滑枕系统的振动特性分析和结构动态特性的优化提供依据。