网格式交直流混合配电网最优潮流计算方法

冯 伟，杨 乐，赵 辛，唐 杰，吴 倩

（1.国网江苏省电力有限公司泰州分公司，泰州 225300；2.东南大学，南京 211189）

0 引言

正常情况下交直流混合配电网主要以辐射式、开环运行等结构为主，但是，直流系统的直流负载会随着交直流的连接而接入、同时可再生能源的大量接入，导致配电网中各类相关设备的数量显著增加，以此导致混合配电网发生能源损耗，降低电能质量[1]，对于交直流配电网的可靠运行造成较大影响。因此，主动配电网的结构逐渐转变成网络式。最优潮流是以给定的配电网结构参数和负荷为前提，对配电网中控制变量实行调节，且该变量为可利用变量，以此满足配电网运行约束条件，保证配电网运行过程中，任一运行目标为最优时的潮流结果[2]，其是保证配电网安全运行的重要部分，同时，是实现交直流混合配电网优化运行的基础。

为计算网格式交直流混合配电网最优潮流，巨云涛等人基于二阶锥规划凸松弛方法，计算最优潮流[3]；金国彬等人提出基于网络矩阵的相关最优潮流计算方法[4]；上述方法均具有潮流计算能力，但是，在应用过程中，对于网络损耗的控制仍需进一步验证。因此，本文针对网格式交直流混合配电网的拓扑结果展开分析，依据该类配电网的运行特点，确定最优潮流计算模型，并对模型实行求解，获取网格式交直流混合配电网最优潮流计算。

1 网格式交直流混合配电网最优潮流计算

1.1 网格式交直流混合配电网运行特点

网格式交直流配电网是智能电网建设过程中，通过主动配电网技术实现配电网从辐射状结构的转换形成的一种配电网结构，其拓扑结构如图1所示。

图1 网格式交直流混合配电网拓扑结构

网格式交直流混合配电网主要由三个部分组成，分别是交流系统、柔性直流输电系统换流站以及直流网络，该类配电网具有更好的供电可靠性，并且具有更好的资源优化配置能力，保证交直流混合配电网中各个电力电子设备的功率调度和控制，接入分布式电源后，提升功率的调度和控制效果；并可更好的实现分布式电源消纳[5]。该类配电网具有上述优势的同时，也存在一定的问题，由于该类配电网中接入大量的分布式电源，导致配电网中发生故障后，保护动作的复杂程度提升，会发生较大的短路电流，对于功率的调度和分配造成影响，影响电压质量，导致电流过大、电力设备损坏等情况，因此，为保证网格式交直流混合配电网的安全运行，需可靠实现配电网中功率的可靠调度。

1.2 网格式交直流混合配电网最优潮流计算模型

本文依据网格式交直流混合配电网拓扑结构和其运行特点，并结合最优潮流的非线性特性，为保证配电网中功率的最佳调度和分配以及电压质量，构建最优潮流计算模型。

1）目标函数

模型的目标函数为最小网损f(x)1min、最小电压偏差f(x)2min，由于网格式交直流混合配电网的网损结果包含多个方面的损耗，如线路损耗、换流器损耗以及直流潮流控制器损耗。则f(x)1min和f(x)2min的计算公式分别为：

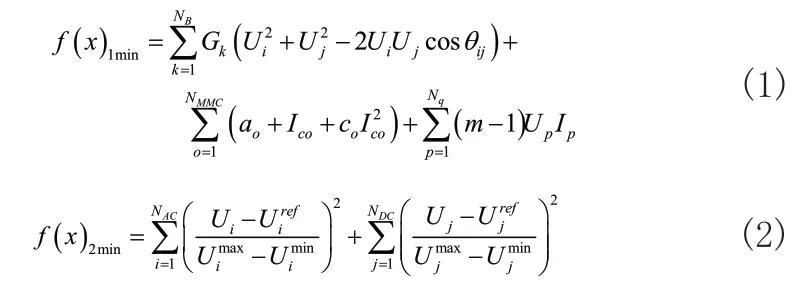
式(1)中：NB、NMMC、Nq分别表集合，依次分别对应线路、换流站节点和直流潮流控制器；线路k的导纳用Gk表示；Ui和Uj均表示电压，前者对应交流节点i，后者对应直流节点j，两者之间的相位差用θij表示；o表示换流器，其恒定和二次两种损耗系数分别用ao、co表示；经过o后发生的损耗电流用Ico表示；电压和电流分别用Up和Ip表示，且对应第p个直流潮流控制器节点；NAC和NDC均表示集合，前者对应交流节点，后者对应直流节点；分别表示i和j的电压参考值，且

2）决策变量

网格式交直流混合配电网最优潮流的决策变量用X表示，其表达公式为：

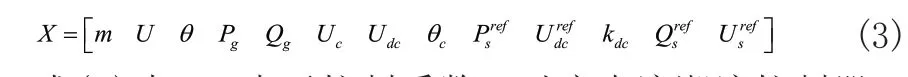
式(3)中：m表示控制系数，对应直流潮流控制器；均表示参考值，前者对应柔性直流输电系统换流站定有功功率，后者对应定直流电压控制；kdc表示曲线斜率，对应下垂控制；均表示控制参考值，前者对应定无功功率，后者对应定交流电压，上述6个参数均属于控制变量。Uc、θc和均表示向量，前者对应电压，后者对应相角，均属于柔性直流输电系统换流站，其属于状态变量。U、θ表示电压和相角两种向量，均属于交流节点；Pg、Qg表示功率向量，均属于发电机，且前者对应有功，后者对应无功；Udc表示电压，对应直流节点；上述5个参数均属于寻优变量。

3）约束条件

网格式交直流混合配电网最优潮流模型的节点功率平衡约束，其主要包含交流和直流两种节点，其计算公式为：

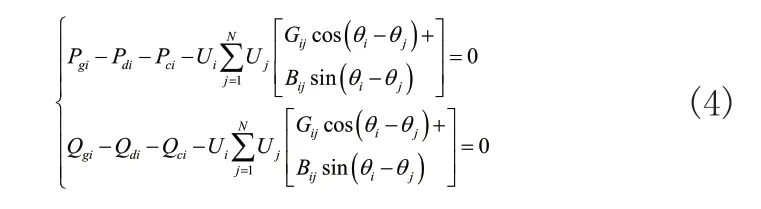
式(4)、式(5)中：P表示有功功率；Q表示无功功率；gi、di、ci分别表示发电机、负荷和换流阀，均和和交流节点i相连接；K0、K1、K2均表示系数；Gij和Bij分别表示节点i和j的电导和电纳。

上述约束条件均为等式约束，除上述等式约束外，潮流还需满足下述不等式约束。

网格式交直流混合配电网交流侧和常规交流最优潮流约束公式为：

式(6)中，Ui表示节点电压幅值，其约束范围在Umax和Umin之间；Pgi表示发电机的有功出力，其约束范围在0和Pgmax之间；无功出力用Qgi表示，其约束范围在Qgmax和Qgmin之间；线路功率和变压器支路功率上下限约束分别用Pij、Pijmax和-Pijmax表示。

直流侧约束条件包含换流阀运行约束和直流线路容量约束，网格式交直流混合配电网稳态运行时，需满足直流母线电压、换流阀容量和电压调制、直流线路输送4个约束条件，也称这四个约束条件为网格式交直流混合配电网的稳态约束条件，其公式如式(7)所示：

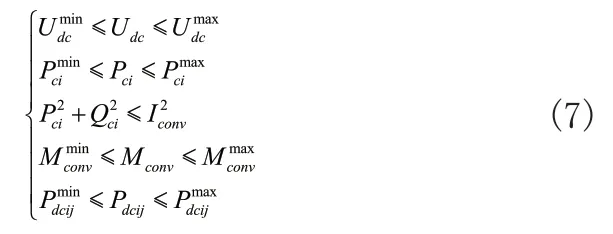
式(7)中：Mconv表示电压调制比，对应换流器，其上下限值为；Pdcij表示由节点i注入j中的有功功率，其约束范围在之间；表示可承载的电流上限，对应换流器内部。

计算网格式交直流混合配电网最优潮流时，需对换流站的输送功率实行调整，在调整过程中，需对配电网实行N-1约束，其约束公式为：

式(8)中，I∈C，表示配电网故障集C中的第k个故障，该故障发生后的约束上下限用表示；gk表示功率平衡方程，对应故障后配电网节点。

1.3 最优潮流模型求解

依据上述小节构建最优潮流模型后，本文采用一种基于元启发式（JAYA）算法，对模型实行求解，该算法具有良好的求解性能，在求解过程中，无需依据特定的参数即可完成有约束条件和无约束条件的目标函数求解。该算法主要是对给定的问题实行循环迭代，且以最优解为目标完成。

将f(x)1min和f(x)2min结合形成综合的最小化目标函数，用minf(x)总表示，对其实行第z次迭代后，可得出决策变量和候选解的数量，分别用n和l表示，此时对决策变量实行调整，该调整公式为：

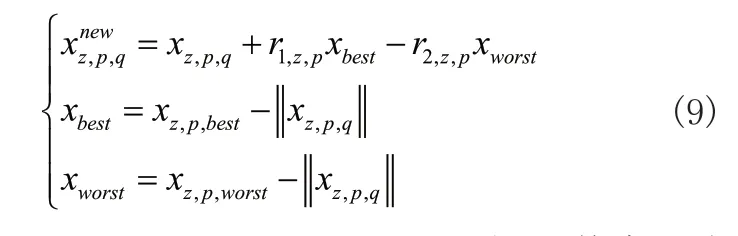
式(9)中，p=1,2,...,n；q=1,2,...,l；r1,z,p和r2,z,p均表示随机数，对应第z次迭代时的第p个决策变量，且取值范围为[0,1]；采用JAYA算法经过第z次迭代后，从第q个候选解中得出的第p个决策变量结果用xz,p,q表示，其新结果用表示；同样在经过第z次迭代后，从b个候选解中得出的第p个决策变量最佳结果和最差结果分别用xz,p,best和xz,p,worst表示；根据两个结果得出网格式交直流混合配电网最优潮流解决策略的趋势分别用xbest和xworst表示。

2 实验结果分析

为验证本文方法的应用效果，以图1的网格式交直流混合配电网为实例测试对象，进行相关测试。该配电网中共有4个直流发电机，2个交流电机，10个电压源变换器，其中变换器4～7与负载相连接；配电网中的10个节点详细参数如表1所示。

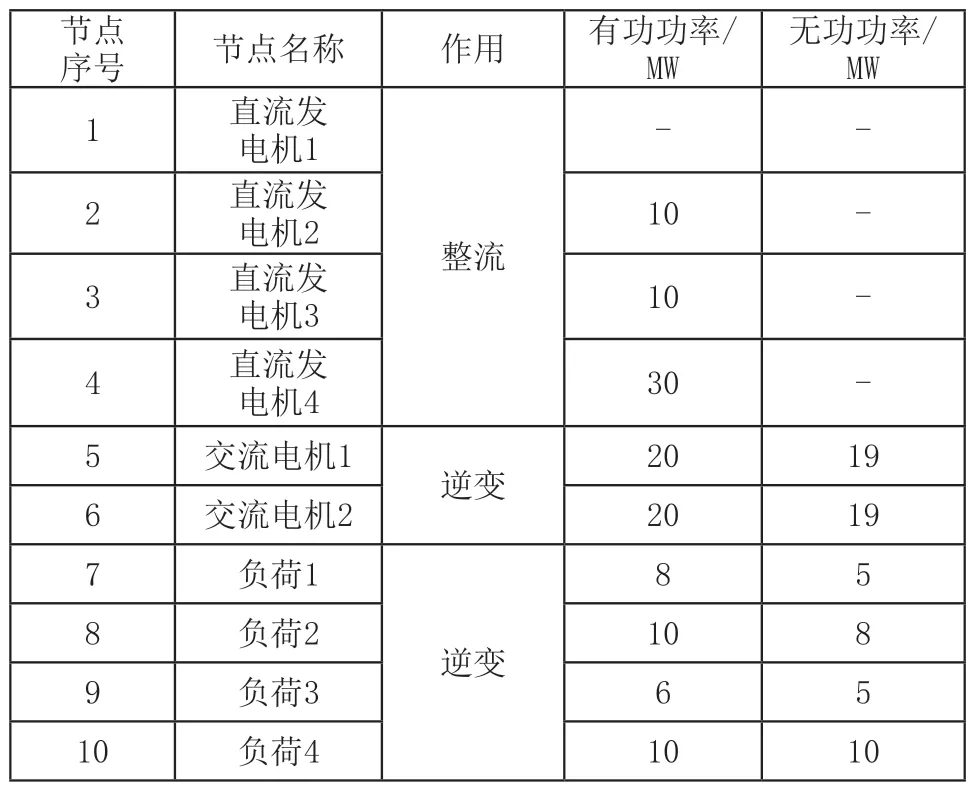
表1 节点参数详情

该配电网额定电压为3.5kV，最大电流值为1.5kA，其中电抗和电阻分别为0.1p.u和0.05p.u，前者属于变压器，后者属于直流电缆。且节点1为电压平衡节点，需保证该配电网中各个节点电压值在0.95～1.05p.u之间；网损结果低于2.5MW，交流节点和直流节点的电压结果与参考值之间的偏差结果小于±0.2。

为衡量本文方法的最优潮流计算效果，采用本文方法对配电网中的所有节点实行计算，获取各个节点的电压和相角计算结果，如表2所示。

表2 各个节点的电压和相角计算结果

测试结果表明：本文方法具有网格式交直流混合配电网最优潮流计算能力，能够获取各个节点的电压结果和相角值，并且电压的计算结果均在0.95～1.05p.u之间，各个相角值均在1.55°以内。因此，本文方法具有良好的配电网最优潮流计算效果，可保证配电网中各个节点的电压处于标准范围内。

为验证本文方法的对于最优潮流的求解效果，通过本文方法求解最优潮流模型，获取配电网不同负荷情况下，最小网损计算结果和交、直流节点之间的最小电压偏差的求解结果，分别如图2和图3所示。

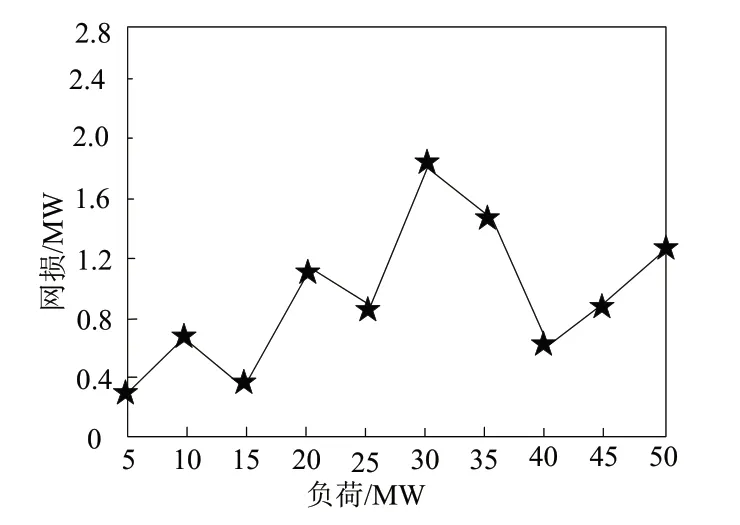
图2 最小网损计算结果

图3 最小电压偏差计算结果

依据图2和图3测试结果可知：该方法具有良好的最优潮流模型求解效果，能够计算得出配电网最小损耗和最小电压偏差结果，随着配电网中的负载的不断变化，网损结果发生小幅度的波动变化，但是变化结果均低于2.5MW，其中，网损最高值为1.8MW左右；交流节点和直流节点的电压结果与参考值之间的偏差结果最高值为±0.05左右，满足应用需求。

为进一步验证本文方法的应用效果，以换流器内部可承载的电流上限作为衡量标准，获取在不同无功功率下，该电流的变化结果，如图4所示。

图4 换流器内部电流越限测试结果

依据图4测试结果可知：随着无功功率的逐渐增加，换流器内部可承载的电流上限结果，在一定范围波动变化，但是整体变化结果均在允许的上限范围内，均低于0.4kA，是由于本文方法在应用过程中，充分考虑换流阀容量和电压调制的相关约束，保证最优潮流，因此，有效避免换流器内可承载电流发生越限情况，保证网格式交直流混合配电网的稳定运行。

为衡量本文方法的应用性能，采用交、直流的电压和电流越限概率作为衡量标准，获取配电网发生不同数量故障情况下，交、直流的电压和电流越限概率结果，如表3所示。

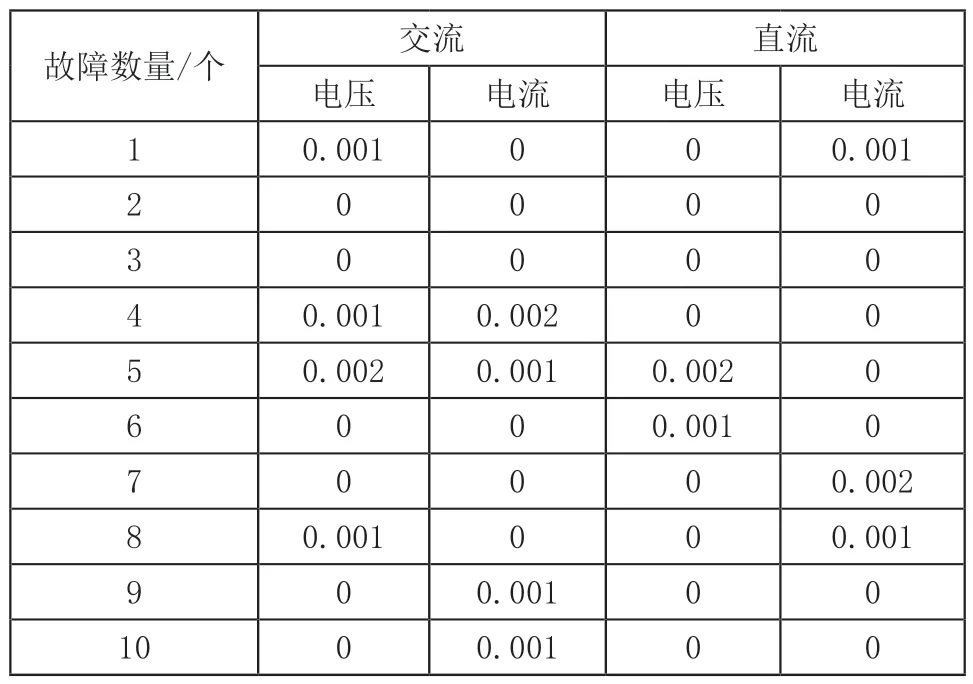
表3 交、直流电压和电流的越限概率结果（%）

依据表3测试结果可知：网格式交直流混合配电网中发生不同数量故障时，随着有功出力的逐渐增加，交、直流电压和电流的越限概率结果均在0%上下，均不超过0.002%，因此，越限概率极小。由于本文方法在应用过程中，可调整换流站的输送功率调整，并需对配电网实行N-1约束，因此，可避免在配电网发生故障的情况下，发生电流和电压越限情况，保证交直流混合配电网优化运行。

为衡量本文方法的应用性，获取本文方法应用后，随着网格式交直流混合配电网中负荷结果的逐渐增加，配电网在暂态和稳态两种运行工况下，电压的稳定裕度结果（要求该裕度结果达到4.0以上），如图5所示。

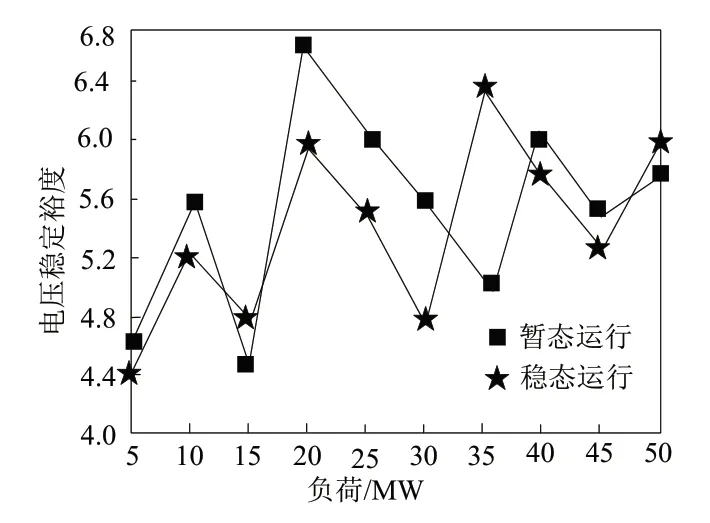
图5 电压的稳定裕度结果

依据图5测试结果可知：在两种运行工况下，随着配电网中负荷结果的不断变化，配电网电压稳定裕度结果也发生一定的变化，其中最小安全裕度结果为4.4左右，最高安全裕度结果为6.7左右，该结果明显优于要求标准，因此，本文方法具有良好的应用性，能够极大程度保证配电网在不同的运行工况下，依旧可稳定运行。

3 结语

网格式交直流混合配电网结构较为复杂，因此其在运行过程中容易产生较大的短路电流，导致网络损耗较高。最优潮流结果直接影响配电网的运行状态，本文提出网格式交直流混合配电网最优潮流计算方法，并对该方法的相关应用情况实行验证。结果显示：本文所提方法具有良好的应用效果，能够满足交、直流侧的各项约束条件，能够对配地网中的多个控制变量实行控制调整，以此可降低网络损耗，优化配电网的潮流分布，保证网格式交直流混合配电网的安全运行。