考虑多因素的自适应遗传算法机器人路径规划
2022-10-29李航宇郭晓利
李航宇,郭晓利
(1.吉林电子信息职业技术学院,吉林 132021;2.东北电力大学 信息工程学院,吉林 132021)
0 引言
移动机器人路径规划技术是机器人领域内重要的研究方向。它是指机器人在一个特定的环境下,从起始点至终点搜索出一条符合约束条件的运行路径,同时完成相应的工作。国内外对机器人路径规划算法有许多的研究,常采用的方法有算法[1]、算法[2]、神经网络算法[3]、人工势场法[4]等。同时随着路径规划问题复杂度的提升,出现了大量的仿生算法,例如蚁群算法[5]、蜂群算法[6]、粒子群算法[7]、遗传算法等。上述算法在机器人路径规划问题上都取得了良好的表现,但是其中大部分算法优化目标考虑的因素不足,无法满足机器人实际中的工作。
遗传算法作为一种优化算法,在机器人路径规划领域内有着大量应用。基本的遗传算法自身有着许多缺陷,因此大批学者对遗传算法进行了改进。魏彤等[8]针对许多算法得出的路径非最短及规划间断问题,提出一种改进遗传算法的路径规划方法。在遗传操作中,加入插入算子和删除算子,提升了算法的计算准确度,获得了最优路径。徐梦颖等[9]提出一种具有自适应策略的遗传算法,该算法模型引入克隆算子及自适应算子,从而防止算法陷入局部极值,并且提高了算法运行效率。孙波等[10]首先利用模拟退火法对种群进行选择,丰富了种群的多样性;同时利用自适应交叉、变异算子和精英策略,加快算法的收敛;另外在适应度函数中加入路径平滑度、拥挤度和车辆质量等三个因素,从而规划出更适应实际环境的路径。
结合上述提到的问题,提出一种考虑多因素的自适应遗传算法进行路径规划,根据实际的运行环境同时考虑路径长度、转向次数及环境坡度等多个因素,另外对遗传操作进行调整,从而提升最优路径的综合性能及算法效率。
1 环境建模及问题描述
机器人路径规划问题指的是在特定的约束下,搜寻出一条最佳路径,可表示为:
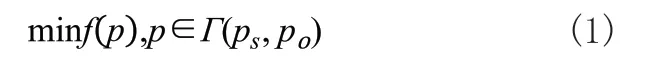
式(1)中,f(p)表示路径的目标函数,ps为起始点,po为目标点,(ps,po)表示起终点之间的路径节点集合。
环境建模是指将实际环境映射至一个抽象空间上。机器人路径规划建模环境主要有栅格图、可视图、自由空间等。其中栅格地图创建简单且管理方便,因此采用栅格图作为仿真环境。在栅格地图中,黑色栅格代表障碍物,白色栅格代表可行区域,利用直角坐标进行定位。为了保证机器人运行的安全,将实际环境转换为栅格图过程中规定,障碍物占用不足一个栅格时将其膨胀为一格,且机器人禁止沿着障碍物边缘运行。栅格地图环境如图1所示。假设栅格地图环境中,栅格标号按从下到上,从左至右的顺序依次增大。栅格地图大小为M行N列,栅格标号为Y,则栅格标号与栅格中心直角坐标换算公式如式(2)所示:
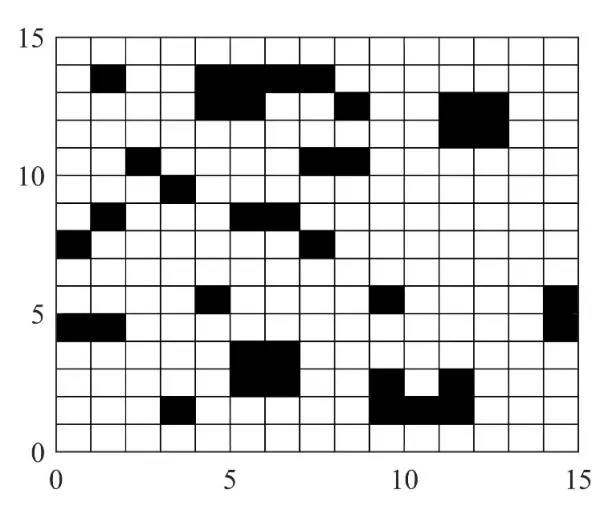
图1 栅格地图

式(2)中,mod表示取余,int指取整。
2 改进遗传算法
2.1 改进适应度函数
遗传算法中适应度函数表示种群中个体质量,它反映了个体可被选入到下代的概率,是整个算法的核心。在基本遗传算法中适应度函数只与路径距离有关,可表示为:
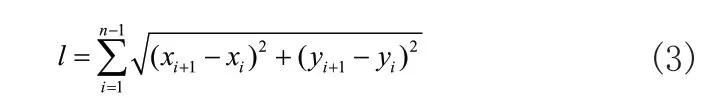
式(3)中只考虑了路径长度,为了提升路径的综合性能,对适应度函数做如下修改:
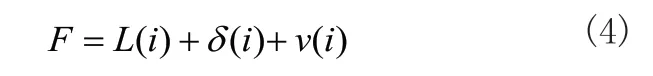
式(4)中表示距离因素,指转向因素,是环境高度。
2.1.1 距离因素
基本遗传算法只考虑路径距离,忽略了邻近个体之间的距离,若它们相隔较远可能会使得可行路径减少,因此必须剔除两点相隔较远的个体,扩大搜索范围。另外,为了提升算法的避障性能,在距离因素中引入惩罚项,减少种群中不良个体数。因此对距离因素做如下修改:
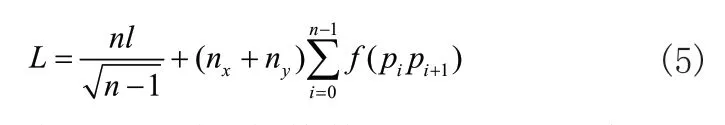
式(5)中,n为路径经过总栅格数,f(pipi+1)表示邻近两栅格之间障碍物的总数。
2.1.2 转向因素
在机器人工作时除了要求路径距离短,还应避免转向次数过多,从而减少自身的损耗。经典遗传算法中没有考虑此因素,可能会导致能耗成本增加。因此在适应度函数中引入转向因素,其表达式如式(6)所示:
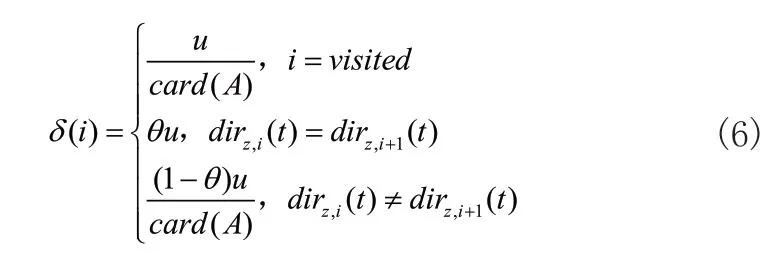
式(6)中,u为常数,θ是一个百分数,反映了直行的重要度,t为当前迭代数,dirz,i为z号栅格转移至i号栅格的转向标号,card作用是求集合元素数目,A为可行栅格集合,visited为已访问的栅格集合。通过式(6),可以有效减少机器人转向次数,从而降低自身损耗,提升使用寿命。
2.1.3 高度因素
在实际的机器人运行环境中,周围环境往往不是平地,经常会遇到高度的变化,因此在遇到坡度变化大的环境时,应该尽量减少爬坡次数且避免经过坡度大的陡坡,从而降低能量的消耗。为使路径更为平缓在适应度函数中加入环境高度函数,公式如下:
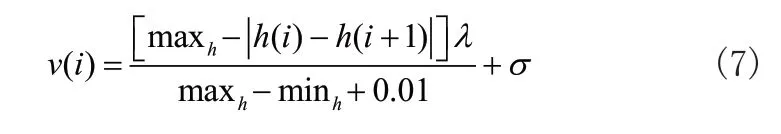
式(7)中,h为高度矩阵,λ,σ指高度修正常数。maxh,minh分别是相邻栅格中与当前栅格的最大和最小高度差,0.01保证分母不为零。
2.2 改进遗传操作
仅通过经典的遗传操作,难以达到良好的避障效果,无法适应机器人实际作业环境。因此本文在传统的操作过程中加入删减及增添算子,具体的改进如下:
1)删减算子。在规划时路径可能会产生自交现象,导致出现无用路径,不利于节省运算空间。因此可以引入删减算子检查路径中是否有重复的栅格,如果存在则表示路径中有自交现象,可以利用删减算子去除此段路经,从而减少无用路径。
2)增添算子。路径中相邻两节点可能出现相距较远,邻域不可达等情形,使得无法找出所有寻优路径。因此通过加入增添算子,保证相邻节点位于同一邻域。如果出现邻域不统一的相邻节点,则在它们之间连线中点处增加一个节点栅格,不断重复此操作,直到路径中所有节点满足条件。
2.3 自适应遗传算子
基本遗传算法中遗传操作的交叉及变异概率是保持不变的,无法适应动态的环境。为提升算法的搜索性能及效率,在遗传操作中采用自适应交叉概率及变异概率,具体公式如式(8)、式(9)所示:
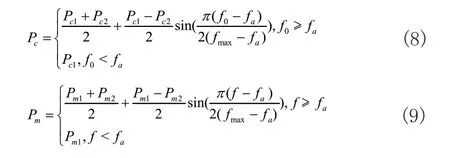
式(8)、式(9)中,pc1和pc2分别为最大及最小交叉概率,pm1和pm2为最大及最小变异概率,f0为交叉时数值更大的个体的适应度,fa为平均适应度值,f为变异个体的适应度大小,fmax为适应度最大值。通过调整变异及交叉概率,可在算法的初期保留更多的优良个体,而在算法后期能防止算法进入局部最优。
2.4 改进算法实现流程
步骤1:建立栅格环境,设置算法参数的初始值。
步骤2:生成遗传算法的初始种群。
步骤3:进行遗传操作,首先进行轮盘赌选择操作,然后根据式(7)和式(8)自适应调节交叉与变异概率,进行交叉与变异操作,产生相应种群。
步骤4:将上一步骤中得到的种群个体,代入式(4)中计算出各自的适应度值。
步骤5:判断本轮迭代是否结束,如果结束继续执行下一步骤,反之则返回步骤3。
步骤6:判断是否达到最大迭代数,若是执行下一步骤,否则,返回步骤2。
步骤7:得到最优的路径。
上述步骤对应的算法流程图,如图2所示。
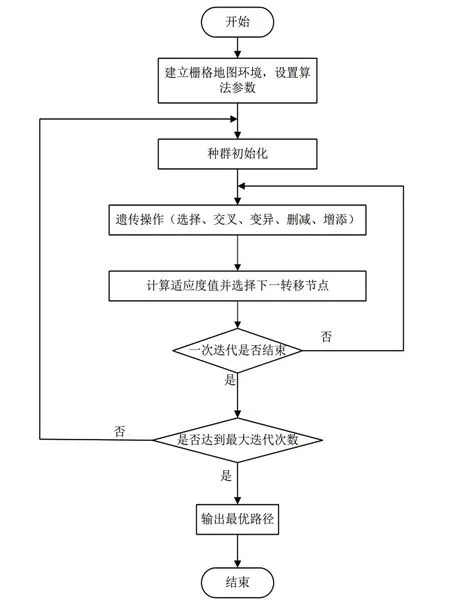
图2 算法流程图
3 仿真实验及分析
3.1 常规环境仿真
基于MATLAB R2017b平台对算法进行实例仿真。其他仿真运行条件为:Windows9操作系统;GPU 2.4GHz;运行内存为8GB。算法主要参数值为:种群规模80,最大迭代数为200,u为20,θ为50%,高度修正常数λ=5,σ=1,选择概率为0.9,变异概率初始值为0.01,最大变异概率为0.1,最小变异概率为0.01,交叉概率初始值为0.7,最大交叉概率为0.8,最小交叉概率为0.6。
栅格地图环境大小为15×15,起点为(0.5,0.5),终点为(14.5,14.5)。其中图中灰色越深表示高度越高。改进遗传算法及基本遗传算法的实例仿真图如图3和图4所示,多次实验得出的各个指标平均值的对比结果如表1所示。

图3 基本遗传算法仿真图
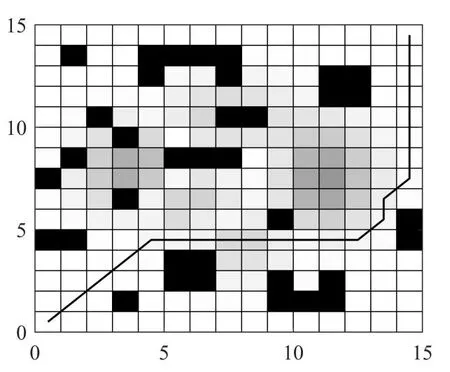
图4 改进遗传算法仿真图
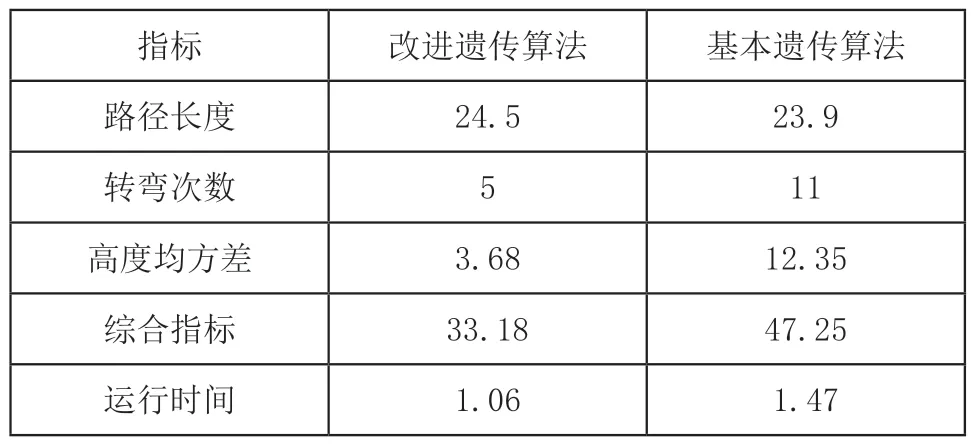
表1 算法结果对比
由图(3)和图(4)能够直观的看出,基本遗传算法规划出的路径转折次数多于改进的遗传算法,另外基本遗传算法无法避开坡度大的区域,而改进的遗传算法则解决了这一问题,其规划的路径更为平坦。从表1能够精确的看出两种算法具体指标上的差异,本文改进算法虽在路径长度上稍逊于基本遗传算法,但是因为改进的遗传算法加入考虑了转弯和高度等因素,在综合指标上明显优于基本遗传算法,且规划速度更快。从上述分析可知,在同一环境下,改进遗传算法的综合表现更好,更加适合机器人的实际工作情景。
3.2 极端环境仿真
在特殊的极端地形下,基于规格的栅格地图进行仿真分析,其他参数值保持不变。改进前后的算法仿真图如图5和6所示。
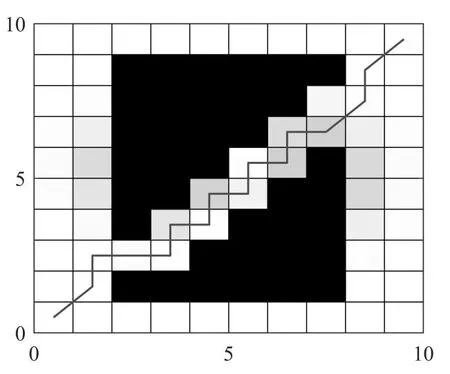
图5 基本遗传算法仿真图

图6 改进遗传算法仿真图
根据以上两图,可以看出在特殊的地形下,改进的算法在转向次数上远少于基本遗传算法,使得机器人在转向上的能量消耗大大减少。因此在极端环境下,改进的遗传算法优势更加明显,展现出更强的环境适应能力。
4 结语
针对当前机器人路径规划算法存在的不足,提出一种考虑多因素的自适应遗传算法,可以得到下列结论:
1)在基本遗传算法的适应度函数中,加入转向及环境高度因素,更加符合实际环境,改进遗传算法得出的路径综合指标得到了较大提升。
2)改进遗传操作中的交叉及变异概率的调节机制,设计了自适应方案,动态调整交叉及变异因子,从而提升算法的计算效率及搜索性能。
3)在遗传操作中,引进删减及增添算子,从而增强算法避障能力。
