冗余驱动并联机构的驱动力协调性优化控制方法
2022-10-29冯建彬李铁军李赛雷
冯建彬,李铁军,杨 冬,李赛雷
(河北工业大学 机械工程学院,天津 300132)
0 引言
冗余驱动并联机器人不但具有传统并联机器人承载能力强、刚度高等优点,而且通过引入冗余驱动,使机构能够有效消除奇异位型[1]和驱动内力[2],提高灵巧性[3]以及动态性能[4],这些优点使冗余驱动并联机器人非常适用于建筑施工。但由于冗余驱动并联机构的驱动数目大于自由度数,使各驱动间耦合更加复杂,机构驱动力协调性将变得尤为重要[5]。
现有对于冗余驱动并联机构的研究主要集中在控制系统设计以及轨迹优化方面。在控制系统方面,沈辉等[6]基于逆动力学分析,提出了一种自适应力位混合方法并通过最小二乘法对驱动力进行了优化分配。Shang等[7]结合主动关节的关节空间和末端执行器的任务空间内存在的两种误差,设计了一种协调控制器,提升了冗余驱动并联机构的轨迹跟踪精度。Niu等[8]提出了一种基于轮廓误差的同步滑膜控制,在参数不确定和没有动态模型的情况下,实现了良好的跟踪性能。Wen等[9]以四自由度冗余驱动并联机构为研究对象,设计了一种基于最优转矩分配的力位混合控制方法,有效减小了转矩波动与位置误差。Zheng等[10]利用内模控制对力位混合控制进行了优化,通过重新设计位置环,提高了整体控制的精度与稳定性。刘晓飞等[11]在传统力位混合控制系统的基础上,利用神经网络设计了一种同步控制器,进一步提高了机构的驱动协调性。同时,对于其轨迹优化方面也有着不少的研究[12~14],主要实现了机构的光滑运动以及时间,能耗等目标的优化。其中陈栋[15]等采用五次B样条曲线在笛卡尔空间内对机构末端轨迹进行了参数化表达并优化求解,在优化轨迹的同时保证了末端轨迹精度以及机构运动的平稳性。
虽然对于冗余驱动并联机构的控制研究已日益深入,但是还没有针对其驱动力协调性进行系统的控制策略研究。本文在力位混合控制的基础上,对机构运动轨迹进行驱动力协调性优化。从而形成从机构运动始末位置的选取出发,到最优协调性轨迹的规划,再到力位混合的控制输入,一套完整的冗余驱动并联机构的驱动力协调性优化方法。
1 冗余驱动并联机构及其控制方法
该冗余驱动并联机构主要应用于建筑施工,可用于幕墙或板材的安装工作,其机构模型及部分构成如图1所示。机构自由度数为三,同时包含六个驱动关节,是一种新型的冗余驱动并联机构。

图1 冗余驱动并联机构模型
通过选取与机构自由度数目相同的伺服电机驱动关节采用位置驱动模式(即非冗余驱动关节),以实现机构的位置控制;剩余气缸驱动关节采用力驱动模式(即冗余驱动关节),以实现各驱动力以及机构内力的调节。相比于传统的位置驱动或者力矩驱动,力位混合驱动不但能够较好的控制机构的运动精度,而且能够有效的调节机构的各驱动关节力矩。对于冗余驱动并联机构而言,这种控制方法可以有效的提高机构的驱动力协调性。本文设计相应的力位混合控制方法如图2所示。

图2 力位混合驱动控制方法
该力位混合控制方法是在轨迹规划的基础上,通过逆运动学计算各位置驱动关节期望输入,通过动力学模型及驱动力优化分配计算各力驱动关节期望输入,然后分别由伺服电机和气缸实现对机构位置和驱动力的控制。同时由于驱动误差的存在,设计位置传感器和力传感器用以反馈机构末端的位置以及冗余驱动关节的力矩大小,实时调节各驱动输入。从而有效提升控制系统的动态特性,较好的改善各驱动间的协调性。但是,整个机构在力矩调节过程中,实际上是利用力驱动关节对位置驱动关节进行的力矩调节。这也就导致在这个调节过程中,由于动力学模型的不准确或存在调节误差,就极易影响机构整体的驱动力协调性。
1.1 逆运动学模型的建立
该机构可以简化为如图3所示的六杆机构,为了便于分析,在关节1处建立固定坐标系{S},在末端中心建立移动坐标系{N}。该机构末端在空间的运动可用位姿参数(x0,y0,γ0)描述,因此定义机构空间运动的广义坐标为:

图3 冗余驱动并联机构简图

其中,[x0y0]T为机构移动坐标系原点ON在固定坐标系{S}中的位置向量,γ0为移动坐标系{N}在固定坐标系{S}中的欧拉角。
假定各驱动关节的关节角为θi,由封闭矢量法,分别得到6个驱动关节的运动学逆解:
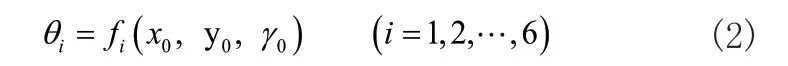
其中fi(.)为逆运动学模型。

其中JR为广义坐标下的冗余驱动关节部分的速度雅克比矩阵,JN为广义坐标下的冗余驱动关节部分的速度雅克比矩阵。继续对式(1)求二阶,三阶导可分别得到各驱动关节的加速度和急动度。

在此基础上便能够根据末端运动轨迹,解算出各位置驱动关节的位置输入值,实现力位混合驱动控制的位置控制部分。
1.2 机构动力学模型的建立与分析
机构动力学模型是对机构进行分析与控制的基础,本文利用虚功原理建立冗余驱动并联机构的动力学模型。为了简化运算,本文在忽略机构各关节摩擦力对机构的影响。
假定杆Li(i=1,2,3,4,h)的质量为mi,转动惯量为Ii,其运动速度为vi,在广义坐标q下的速度雅克比矩阵为Ji,则:
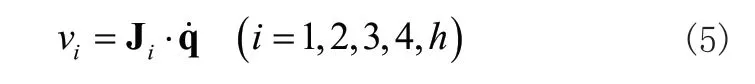
根据达朗贝尔原理,则虚加于各运动杆件上的广义惯性力为:

综上分析可知,各杆的重力所做的虚功为:

各杆的惯性力和惯性力矩所做的虚功为:

假定动平台负载对动平台施加的外力为F。可求得动平台重力,负载对机构动平台所施加的外力所做的虚功:

另,各关节驱动力矩所做的虚功为:

机构在运动过程中主要受重力、惯性力、驱动力以及外负载等的影响,借助虚功原理,建立机构的虚功平衡方程,即:
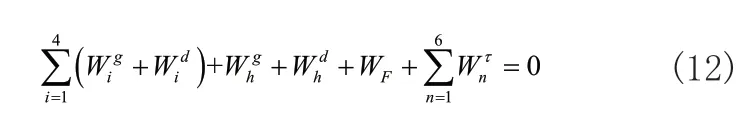
将式(3),式(8)~式(11)分别代入式(12)中,并将略去,可得:

若通过矩阵的广义逆理论,以驱动力为最小二范数解来进行优化分配,可得:
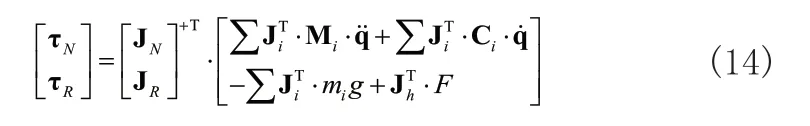
在此基础上,便能够根据机构运动轨迹以及外负载大小解算出各力矩驱动关节的力矩输入值,实现力位混合控制的力控制部分。
然后以τR作为独立变量,将式(12)进一步整理可得:

若机构负载外力及运动状态不变,由式(10)可得:

根据矩阵分析理论可知:||(JN)-T(JR)-T||反映了由冗余驱动力空间向非冗余驱动力空间映射时驱动力调整量广义长度的缩放比例,可表征冗余驱动对非冗余驱动的力矩调节能力[5],其大小与机构运动轨迹有关。机构在力位混合驱动模式下,过大的力矩调节能力将导致力矩调节误差的增大,不利于机构的驱动力协调控制。因此可以通过合理优化机构运动轨迹,避免力矩调节能力过大,从而进一步提升机构的驱动力协调性。
2 末端轨迹的参数化表达及优化求解
2.1 基于B样条曲线的末端轨迹参数化
一条具有n+1个控制点的k阶B样条曲线,其曲线的一般方程为:

式(17)中,di(i=0,1,…,n)为n+1个控制顶点,u=[u0,u1,…,un+k+1]为k次B样条轨迹曲线定义域节点矢量,Ni,k(u)(i=0,1,…,n)为k次规范B样条基函数。
在考虑轨迹精度与计算效率的情况下,本文选用具有11个控制点的五次B样条曲线将机构的末端轨迹表达为:

其中是第i个控制点的广义坐标:

由于在实际工作中,需要机构的末端能够从任意的初始位姿点到达目标位姿点,且始末位姿处的速度、加速度均为零,所以需要轨迹的前三个控制点坐标与初始位姿相等,最后三个控制点坐标与目标位姿坐标相等,即:


按照区间比例关系映射后,可得到第i个有序化的控制点坐标为:

此外,为保证曲线经过其设置的初始和终止位姿点,将其初始和终止节点向量重复k+1次,即u0=u1=…=uk=0,un+k=un+k+1=…=un+2k=1。在此基础上,根据累计弦长参数化方法对时间节点归一化,即:

其中,Δti=ti+1-ti。
在此基础上,根据de Boor-Cox递推公式计算其各阶导数曲线,可分别得到速度,加速度和急动度曲线如下:
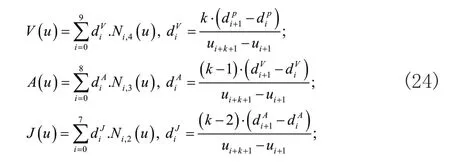
2.2 基于免疫算法的驱动力协调性优化求解
通过机构运动学与动力学分析,选取轨迹上的n各位姿点的||(JN)-T(JR)-T||平均值来评价机构沿该轨迹运动时的驱动力协调性。同时考虑机构各位置驱动关节角位移,角速度,角加速度的约束,可以建立如下轨迹优化模型。需要说明的是,考虑到机构采用力位混合驱动,末端执行器的轨迹仅与三个位置驱动模式关节有关,所以仅对三个位置驱动模式关节进行速度,加速度约束。

随后利用免疫算法进行优化求解,流程如图4所示。
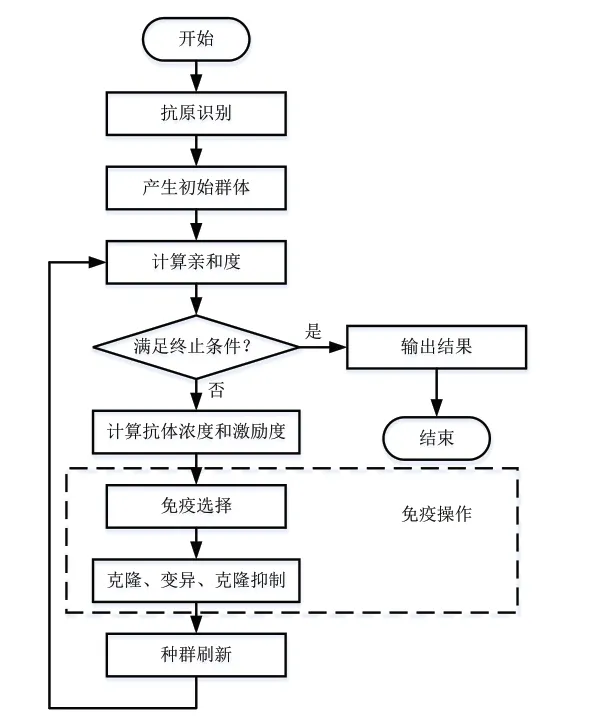
图4 免疫算法流程图
机构各部件的长度如表1所示。根据表2~表3对机构各关节位移、速度、加速度进行约束。

表1 冗余驱动并联机构的各关节角转动范围

表2 机构各部分尺寸

表3 位置驱动关节的速度和加速度约束
设定运动的初始位姿及末端位姿分别为Pi=[420 1220 0°]T,Pf=[950 1670 10°]T。同时为了保证机构的工作效率,设置机构末端的最大运动时间为tmax=10s。免疫算法参数设置为:初始化免疫个体维数为D=21,免疫种群个体数为NP=100,最大免疫代数为G=500,变异概率为Pm=0.7,激励度系数为alfa=1,belta=1,相似度阈值为detas=0.2,克隆个数为Ncl=10。经过计算得到以下协调性最优轨迹参数,以此得到机构末端位姿分量x,y,γ的运动轨迹如图5所示。然后结合逆运动学分析,得到各驱动关节运动轨迹如图6和图7所示。

图5 末端各位姿分量运动轨迹


图6 各关节角位移曲线

图7 位置驱动关节速度,加速度,急动度曲线
由图6、图7可以看出,该轨迹优化方法在满足机构物理约束条件的情况下,实现了机构的光滑运动。在实际工作中,可以在工作空间内设置任意初始和终止位姿,通过该轨迹优化方法实现机构运动始末加速度均为零的平稳启停。同时,优化后的轨迹避免了机构运动在过程中力驱动关节对位置驱动关节产生较大的调节能力,从而有效减小力调节误差,提高机构的驱动力协调性。在此基础上,通过动力学计算便可以得到各力驱动关节的力矩输入值,从而实现冗余驱动并联机构的力位混合控制。
3 结语
本文提出了一种冗余驱动并联机构的驱动力协调性优化控制方法。该控制方法可根据工作需要设置任意始末位置进行轨迹优化,并在此基础上进行力位混合控制,根据运动学模型计算位置驱动关节输入,根据动力学模型进行力矩优化分配计算力驱动关节输入,实现机构的驱动力协调性优化。同时,该控制策略具有很强的通用性,可为其他冗余驱动并联机构提供参考。
