傅里叶变换下Kramers-Kronig关系的理论推导*

苏红梅

(罗定职业技术学院教育系，广东 罗定 527200)

Kramers-Kronig关系(简称K-K关系)最早是由Kramers和Kronig利用原子气体模型推导出来的，他们给出了介电函数及复折射率的实部和虚部之间的色散关系，并将色散关系成功地应用于X射线的色散实验中.K-K关系被推导出来以后，学者经常将其应用于各种材料的光学研究中.如光学常数测量和计算过程中[1]，K-K关系因具有优于其他常规光学测量方法的特性，成为获取光学常数的一种基本方法，对各种各样的材料都适用.笔者拟利用傅里叶变换[2-4]，从物理实验事实的因果律出发，脱离具体的微观物理模型，从数学角度推导K-K关系的表达式，从纯粹的数学性中发现其蕴含的应用的普适性.

1 傅里叶变换简介

傅里叶变换是一种分析信号的方法，其过程是将一个时域非周期的连续信号，转换为一个频域非周期的连续信号.在不同的研究领域，傅里叶变换具有不同的形式.本研究中主要运用连续傅里叶变换，将时域空间和频域空间的函数进行相互转换.这里假定函数f(t)满足傅里叶变换的要求，那么函数f(t)的傅里叶变换为

其中F(ω)称为f(t)的像函数，f(t)称为F(ω)的原像函数.F(ω)的傅里叶逆变换为

(1)

2 K-K关系的推导

凡是由因果关系决定的光学响应函数，其实部和虚部之间都不是相互独立的，用来描述这些响应的每一对宏观的光学常数(如n和κ，ε′和ε″，r和θ)之间都存在一定的内在联系.基于一定的微观物理模型，通过一些物理关系，可以解出宏观光学常数的表达式，找到它们之间的内在联系；从基本的物理量性质及基本的物理条件考虑，利用数学计算方法也可以推导出它们之间的函数关系和内在联系，如在光学常数测量和计算中经常用的K-K关系.接下来，将从介电常数出发对K-K关系进行详细推导.

在电磁学中，用极化率和电场强度之间的关系来描述各项同性、非磁性的均匀介质的线性响应，线性响应关系式为

p(t)=ε0(εr-1)E(t),

其中ε0,εr分别是真空介电常数和介质的相对介电常数.利用傅里叶逆变换(1)式可得

(2)

考虑到极化矢量可能滞后，将(2)式改写为

其中

G(t′-t)称为响应函数，它描述了t′时刻的δ电场脉冲造成的t时刻的电极化，是εr(ω)-1的傅里叶积分.傅里叶逆变换可以表示为

(3)

因为因果律要求在加电场之前没有响应，所以(3)式中的G(T)在T<0时，有G(T)=0.于是，εr(ω)-1为一个在ω复平面上半空间是解析的函数，并在上半平面内对ω的微商是收敛的，当沿着图1所示积分路径积分时，积分结果为0.具体环路积分表达式为

(4)

(4)式中的积分区间为(-∞,ω-δ)和(ω+δ,+∞)，在δ→0的极限情况下，积分值就是沿实轴的柯西积分主值.根据留数定理和初等色散理论[5-6],εr(ω)-1的积分表达式为

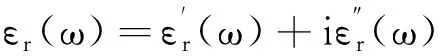
(5)

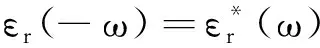
(6)

又因为

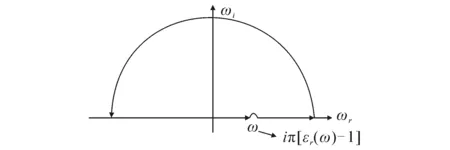
图1 积分路径Fig. 1 Integral Path

所以将(6)式代入方程组(5)可得K-K关系的另一种形式：

(7)

也即εr(ω)的实部和虚部之间的色散关系.

3 K-K关系的微分形式

在实际的物理应用中，为了突出某些特征或考虑到光学响应函数在高低频的收敛性质，会将K-K变换的积分形式转化为微分形式，这2种形式可以形成互补作用.对方程组(7)中实部函数表达式进行凑微分、分部积分，计算出实部、虚部的具体微分表达式如下：

可以看出，变换由两部分组成，即微分因子和对数形式的权重因子.对于权重因子而言，只有ω→ω′时才有明显贡献，如图2所示.

图2 ω=ω′附近贡献最大Fig. 2 Largest Contribution to the Near ω=ω′

至此，得到K-K关系的3种较常用的形式，即被积函数有界、线性响应关系和因果律，因为这些关系非常适用于输入输出线性关系的物理量，所以在物理学的很多分支领域都有重要的应用.K-K关系是无量纲的表达式，它可以不依赖于任何模型而存在，还能极大方便物理参数测量，如为了得到响应函数的相位需要相对复杂的技术和系统，而根据K-K关系只需要简单测量消光谱就可以计算出来.

4 K-K关系的其他表示形式

对于不同的物理背景，K-K关系还有其他的表示形式，如折射率和消光系数之间的n-κ关系：

(8)

因为

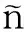
5 结语

K-K关系具有优美的数学形式和普遍的物理内涵，其表达式具备应用的普适性，虽然公式的导出不需要任何物理模型，但却是物理实在(Physical Reality)的高度数学概括.由于因果性条件的保证，K-K关系理论上能应用到任何物理实在中，如已知的反射和透射响应函数、复介电常数、复折射率、复电导率、电阻抗、复磁导率、复原子散射因子、绝热压缩系数、声折射率、单边带时域信号、空间K-K介质及各种非线性介质等[1,7-9]，可以相信，K-K关系的应用领域会越来越广.

当然，在应用中K-K 关系也有不足之处.如K-K积分一般都是在[0，+∞)之间，但由于实际能够测量的物理模型或已知的变量范围总是有限的，会给计算结果带来截断误差，因此需要借助各种积分范围的外推方法来减小误差.目前关于K-K关系的最新研究进展发现，在时域和空域也有K-K关系[7]，未来在这2个发展方向应该会有全新的概念和应用.