改进Rife-Vincent(Ι)窗的FFT介质损耗角测量*

张志威，彭 昊，谭宇豪，李明皓，汪旭明

(吉首大学信息科学与工程学院，湖南 吉首 416000)

介质损耗角是衡量电气设备绝缘性能的重要指标之一，介质损耗角的精确测量对于电力设备的安全、可靠运行起到重要作用[1].介质损耗角的数值小，传统硬件测量方法的测量精度较低，而软件法处理方式较灵活且精度高[2].在软件法中，快速傅里叶变换(Fast Fourier Transform，FFT)因具有便于嵌入式实现、抗干扰性强等特点，成为介质损耗角测量的常用方法.然而，通过电压互感器、电流互感器测量得到的电压、电流信号存在非同步采样，导致对信号FFT处理时会出现频谱泄漏，从而降低介质损耗角的测量精度.为了提高介质损耗角的FFT测量精度，研究者提出了加窗与插值相结合的FFT介质损耗角测量方法[3-6]，以及对信号FFT处理后的谱序列进行加权变换的方法[7].为了更好地监测电力设备的绝缘性能，从窗函数复杂度和测量精度角度综合考虑，笔者认为，仍需对基于FFT的介质损耗角测量方法作改进.

1 介质损耗角测量原理

绝缘材料可以用电阻和电容的并联模型来等效替代，对绝缘材料两端加电压，电介质等效电路见图1.图1(a)中C为介质等效电容，R为介质等效电阻，iR为流过电阻的电流，iC为流过电容的电流；图1(b)中u和i分别为绝缘材料的电压和电流向量，iR和iC正交，φ为u和i的相位差，介质损耗角δ为φ的补交[8].设电容两端电压和电流表达式分别为

u(t)=Au1sin(2πfu1t+φu1),

i(t)=Ai1sin(2πfi1t+φi1).

(1)

其中：Au1和Ai1分别为电压和电流的幅值；φu1和φi1分别为电压和电流的初相角；fu1和fi1分别为电压、电流的频率.介质损耗角δ的计算公式为

(2)

其中φ=|φu1-φi1|.

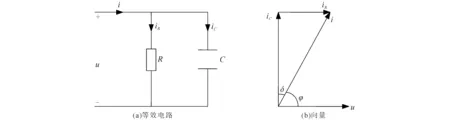
图1 电介质等效电路Fig. 1 Dielectric Equivalent Circuit

2 Rife-Vincent(Ι)自乘窗特性与介质损耗角计算

2.1 改进Rife-Vincent(Ι)窗的旁瓣性能

在FFT介质损耗角测量方法中，窗函数旁瓣性能的优劣决定了测量的精度.笔者设计了一种新的窗函数，新窗由五项Rife-Vincent(Ι)窗自乘得到，用RVSM表示.Rife-Vincent(Ι)窗用RV表示，表达式为

图2 窗函数的幅频特性Fig. 2 Amplitude-Frequency Characteristic of Window Function

其中：m为项数；am为系数；N为窗函数长度；n=0,1,…,N-1.这里a0=1，a1=1.6，a2=0.8，a3=0.228 57，a4=0.028 57.Rife-Vincent (Ι)自乘窗的表达式为

wRVSM(n)=wRV(n)wRV(n).

Hanning窗、Blackman窗、Rife-Vincent(Ι)自乘窗的幅频特性如图2所示.从图2可以看出，Rife-Vincent(Ι)自乘窗的第一旁瓣比Blackman窗、Hanning窗的低，且旁瓣衰减速度更快.

2.2 基于改进Rife-Vincent(Ι)窗的FFT介质损耗角测量原理

测量介质损耗角需要先计算出电压、电流信号的相位，再通过(2)式求得介质损耗角.为了更好地分析基于改进Rife-Vincent(Ι)窗的FFT介质损耗角测量原理，对(1)式中的电压信号进行离散化，得到

(3)

其中fs为采样频率.为了方便窗函数的截断，信号的长度与窗函数相同.对(3)式用Rife-Vincent(Ι)自乘窗截断后进行离散时间傅里叶变换，得到

(4)

(5)

由于信号的非同步采样，频域中实际频率很难对应频域谱线.设ku1=kud+αu，其中kud为频域最大幅值谱线序号，αu为频率偏移量，αu∈[-0.5,0.5].结合三谱线插值算法[4]，不难找出幅值最大的3根谱线为U(kud-1)，U(kud)，U(kud+1)，其中kud-1=kud-1，kud+1=kud+1.令

(6)

由(6)式可知βu和αu可构成函数关系式βu=g(αu)，利用多项式拟合可计算出αu=g-1(βu)的近似多项式.根据搜寻获得的三谱线幅值所含信息[4]，当N较大时，联合(5)和(6)式可得

(7)

(7)式可简化为

(8)

其中

通过多项式拟合也可计算得到O(αu)的近似多项式，代入到(8)式就可计算出幅值Au1.相位修正公式为

(9)

与电压信号的相位测量方法相同，电流信号同样可以利用(9)式计算出(1)式中电流信号的相位φi1，再利用(2)式计算得到介质损耗角δ.介质损耗角δ的计算流程如图3所示.

图3 计算介质损耗角的流程Fig. 3 Flow Chart of Dielectric Loss Angle Calculation

3 仿真实验

为了验证Rife-Vincent(Ι)自乘窗介质损耗角测量方法的有效性，将其与加Hanning窗方法、加Blackman窗方法进行对比实验.采用文献[6]中的仿真模型，一个由基波、3次谐波、5次谐波构成的复合信号，信号基波频率为49.5 Hz，介质损耗角的理论值为0.004 019 04 rad，采样点数为1 024，采样频率为1 280 Hz.仿真结果见表2.

表2 不同窗函数方法下的介质损耗角测量结果

由表2可知，Rife-Vincent(Ι)自乘窗方法介质损耗角的测量精度比加Hanning窗方法、加Blackman窗方法的高出接近9个数量级.

4 结语

设计了基于改进Rife-Vincent(Ι)窗的FFT介质损耗角测量方法，构造的Rife-Vincent(Ι)自乘窗旁瓣特性优于传统窗函数，在很大程度上可以抑制频谱泄漏的影响.仿真实验结果表明，Rife-Vincent(Ι)自乘窗方法比加Hanning窗方法、加Blackman窗方法的介质损耗角测量精度更高.为了进一步提高窗函数的旁瓣特性，可以对Rife-Vincent(Ι)自乘窗自卷积，加快旁瓣的衰减速率，从而更好地减少频谱泄漏的影响.