基于遗传算法优化LSSVM的初速预测

田珂，王荣江，郭丰

(中国人民解放军63861部队，吉林 白城 137001)

利用初速雷达测试弹丸炮口初速的靶场试验中，为了准确鉴定某型坦克炮的射击性能，需要两台初速雷达同时参试，每发弹丸提供2个初速数据。当遇到雷达死机、红外未启、火炮故障等异常情况时，就会缺失某些弹丸的初速数据，所以通过建模预测出缺失的初速数据就很必要。目前预测初速的方法有很多[1-4]，GM(1,1)灰色模型适用于数据本身呈指数变化规律的情形，所以预测初速的精度不高[5]，组合模型也只是在单项模型的基础上提升预测精度[3]，仍然难以达到初速雷达1‰的误差标准。因此，为了提升预测精度，选择把两台初速雷达的数据进行深度融合，一台雷达的相关数据作为输入向量，另一台雷达的初速数据作为输出向量，建立遗传算法优化LSSVM非线性模型进行预测。最小二乘支持向量机(LSSVM)适合作为小样本非线性数据序列的预测模型[5]，同时利用遗传算法对其进行参数优化，可以极大提高预测弹丸初速的精度。引入ARIMA模型、GM(1,1)模型、支持向量回归机和BP神经网络作为对比。实验结果表明，遗传算法优化LSSVM模型预测出的初速数据与实测值最为接近，且误差小于1‰，更适合作为弹丸初速的预测模型。

1 雷达数据融合的原理

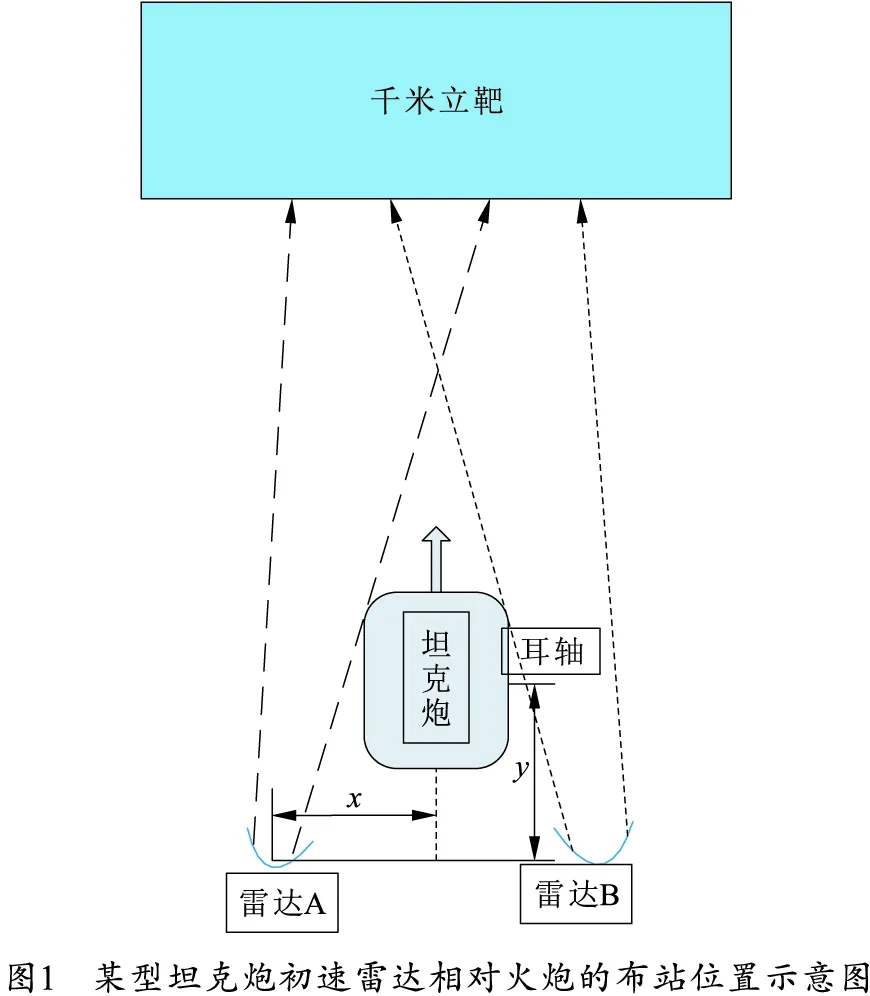
在测试坦克炮初速的具体试验中，两台初速雷达是对称布置在火炮的两侧，两台雷达相对火炮的布站参数是基本一致的，具体的布站位置如图1所示。影响雷达测试精度的因素通常为雷达的后正y和左正x。假设当雷达B的初速数据出现缺失时，选择把雷达A的左正、后正和初速数据作为预测模型的输入向量，雷达B的初速数据作为预测模型的输出向量，然后再把雷达B缺失的初速数据对应的雷达A的左正、后正和初速数据代入到建立好的模型，就可以预测出雷达B缺失的初速数据。

2 最小二乘支持向量机原理

最小二乘支持向量机(LSSVM)是在标准支持向量机(SVM)的目标函数中增加了误差平方和项，用等式约束条件代替不等式约束条件，求解过程变为解一组等式方程[6]。原理是指当给定一组样本数据{xi,yi}，i=1,2,…,n,xi∈Rn表示输入样本，yi∈R表示对应的输出样本，n表示样本的数量，通过训练样本数据，找出相对“平滑”的函数逼近样本集的输入、输出关系，当有一组新的输入时也能给出相对准确的输出[7]。最小二乘支持向量机的拟合问题区分为线性问题和非线性问题。针对线性问题而言，其回归函数为

f(x,α)=ωx+b,

(1)

式中，ω为权向量。

针对非线性问题，可以用核函数代替内积函数，即k(x,xi)=φ(x)φ(xi)，回归方程就变为[8]

(2)

3 遗传算法优化LSSVM原理

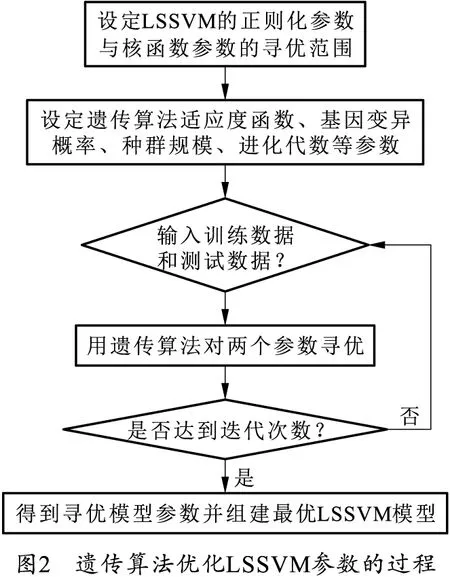
选择把雷达A的左正、后正和初速作为输入，雷达B的初速作为输出，利用两台雷达已测历史数据建立最小二乘支持向量机(LSSVM)模型，然后再把雷达A的输入带入到所建模型中，就可以预测出雷达B的初速。要准确预测出雷达B的初速，就必须建立优质的最小二乘支持向量机模型，关键就是要确定建立模型的最佳参数。遗传算法是一种借鉴生物界自然选择和自然遗传机制的随机搜索算法，能够在搜索过程中自动获取和积累有关搜索空间的知识，并自适应地控制搜索过程以求得最优解[9]。遗传算法将问题的求解表示为“染色体”，该算法从一群染色体串出发，根据适者生存的原则，从中选择出适应度高的染色体个体进行复制，通过交叉、变异两种基因操作产生新一代的、更适应环境的“染色体”种群，随着遗传算法一代一代的运行，那些适应度高的模型将在后代中呈现指数级增长，最终得到适应度最高的染色体，即优化问题的最优解[6]。根据最小二乘支持向量机的建模原理可知，正则化参数γ与核函数的参数σ是影响最小二乘支持向量机预测精度的主要因素，所以选择利用遗传算法搜寻出最小二乘支持向量机的两个最佳参数。遗传算法利用遗传算子对种群中的个体进行操作，通过不断交换染色体信息，使种群得以进化，最终使适应值好的个体得以保留，而适应值差的个体在进化过程中被逐渐淘汰[10]。利用遗传算法搜索LSSVM的正则化参数γ与核函数的参数σ的步骤如图2所示。

4 实验验证

实验选择利用RStudio软件环境进行数据分析、统计建模及数据可视化。为了验证遗传算法优化LSSVM模型预测弹丸初速的精度高于其余模型，选择利用初速雷达测试的某型坦克炮试验数据进行验证，具体的数据如表1所示。

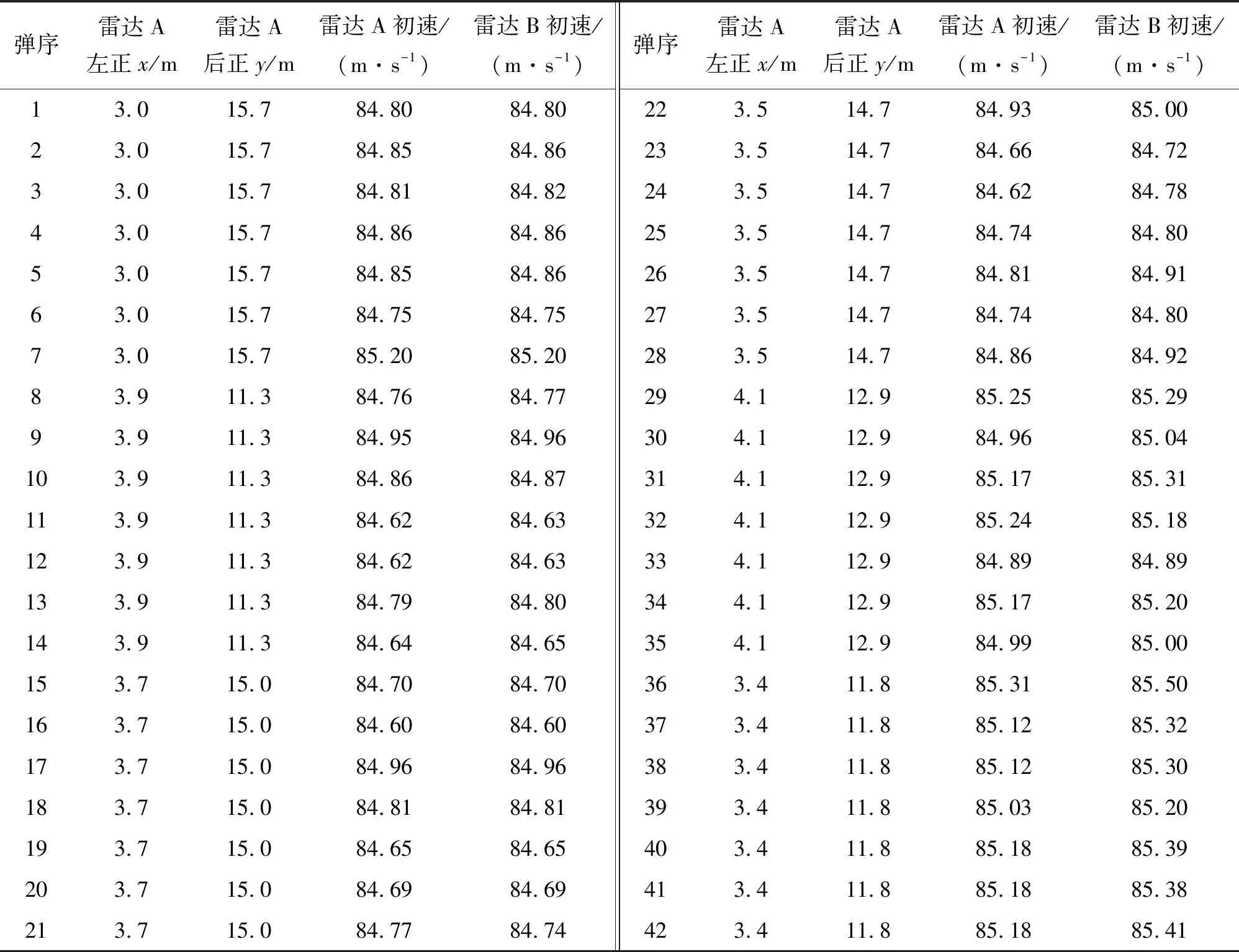
表1 初速雷达测试坦克炮初速实测值DATA1

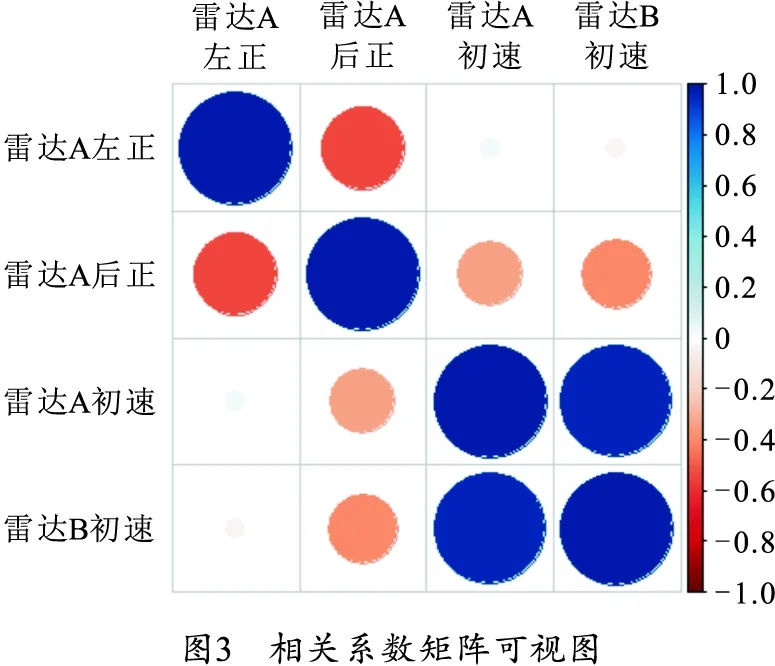
为了检验雷达A的左正、后正和初速与雷达B初速之间的关联性，是否有利于提升预测雷达B初速的准确性，把雷达A的左正、后正和初速作为自变量，把雷达B的初速作为因变量，计算自变量与因变量之间的相关系数如表2所示，绘制相关系数矩阵如图3所示。结合表2和图3可以得知，所有的相关系数均不为0，说明自变量和因变量之间存在因果关系，是存在相关性的[11]，所以把雷达A的左正、后正和初速作为自变量可以提升预测雷达B初速的准确性。

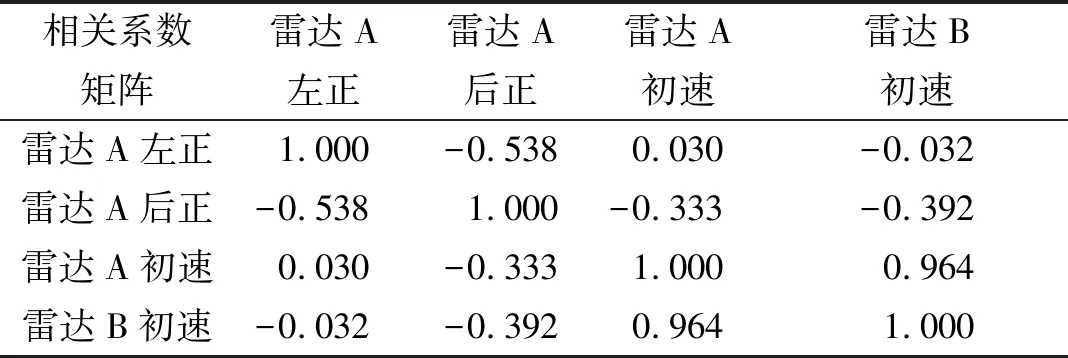
表2 相关系数矩阵

选择将表1中的第1～35行作为训练数据，将第36～42行作为测试数据，将第1～3列作为输入向量、第4列作为输出向量。利用遗传算法优化最小二乘支持向量机的参数，主要是优化RBF径向基核函数的参数和正则化参数，核函数的参数表示在更高维特征空间中数据点分布的离散程度，而正则化参数主要是在最小二乘支持向量机模型中的回归函数两项中起到平衡调节的作用[12]。针对遗传算法优化LSSVM模型而言，把训练数据第1～35行中的第1～25行再作为训练数据，第26～35行再作为测试数据，并把该测试数据的均方误差最小值作为适应度函数，核函数参数和正则化参数的寻优范围设置为0到1 100，种群规模设置为900，迭代次数设为200，基因变异的概率设为0.001，最后搜寻出的最优参数，核函数参数为9.198 092，正则化参数为1 098.164 304，把这两个参数重新代入到模型中就可以预测出雷达B第36～42发初速数据。把ARIMA模型[3]、GM(1,1)模型、支持向量回归机和BP神经网络模型作为对比模型，同样利用训练数据进行建模预测，就可以得到相应的预测值。支持向量回归机的核函数选择径向基核函数。BP神经网络选择3层网络结构，根据经验公式[13]确定隐含层的神经元个数为6。表1中雷达B第36～42发初速实测值与所有模型的预测值如表3所示。

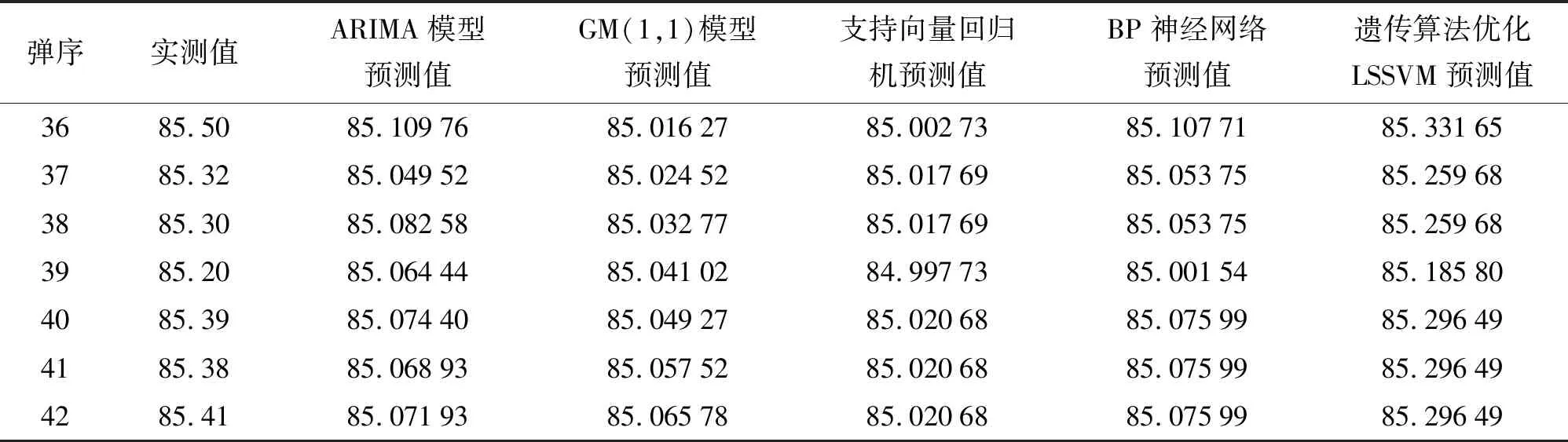
表3 初速雷达B(DATA1)第36～42发实测值与所有模型预测值 m·s-1

根据表3的具体数据可以准确地看出，遗传算法优化LSSVM预测值最接近实测值。经过计算得出：ARIMA模型预测值与实测值的平均相对误差为0.331%；GM(1,1)模型预测值与实测值的平均相对误差为0.370%；支持向量回归机预测值与实测值的平均相对误差为0.402%；BP神经网络预测值与实测值的平均相对误差为0.344%；遗传算法优化LSSVM预测值与实测值的平均相对误差为0.096%。所以遗传算法优化LSSVM预测弹丸初速的误差最小，预测精度最高。此外，遗传算法优化LSSVM的预测值与实测值的绝对误差，以及实测值乘以1‰的误差标准如表4所示。

从表4可以看出，除了第36、40、42发遗传算法优化LSSVM预测值与实测值的绝对误差大于实测值乘以1‰的误差标准以外，第37、38、39、41发的绝对误差均小于误差标准，所以遗传算法优化LSSVM预测弹丸初速整体的精度是满足要求的，单项预测精度也基本满足要求。

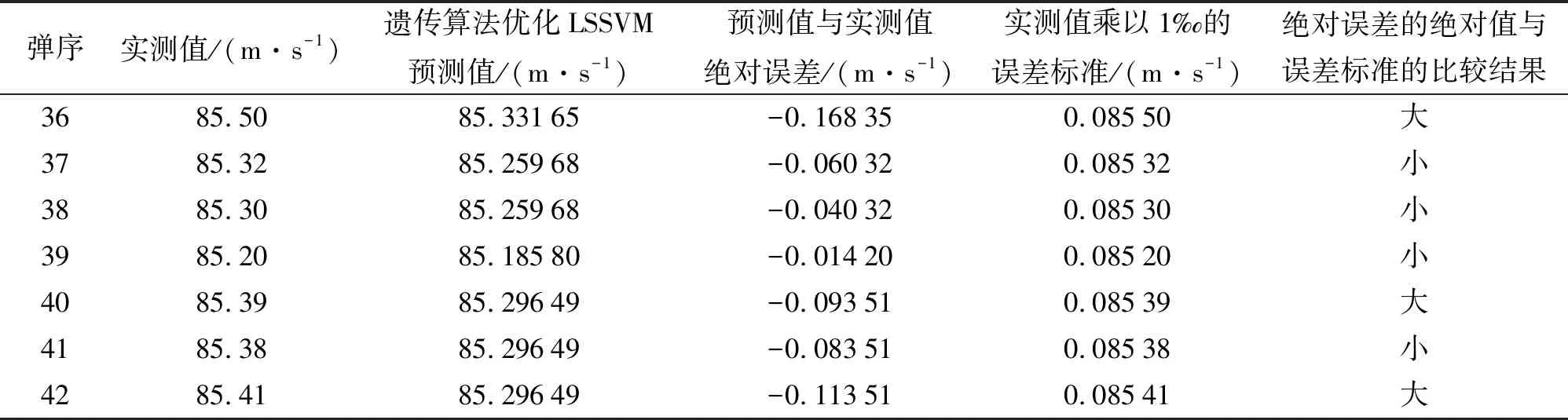
表4 遗传算法优化LSSVM预测值与实测值的绝对误差及误差标准

选择两台初速雷达测试的另一种坦克炮弹的初速数据(共43发)再次进行验证，把第1～35发初速数据作为训练数据，第36～43发初速数据作为测试数据，采用同样的建模预测方法得到雷达B第36～43发初速实测值与所有模型预测值，如表5所示。

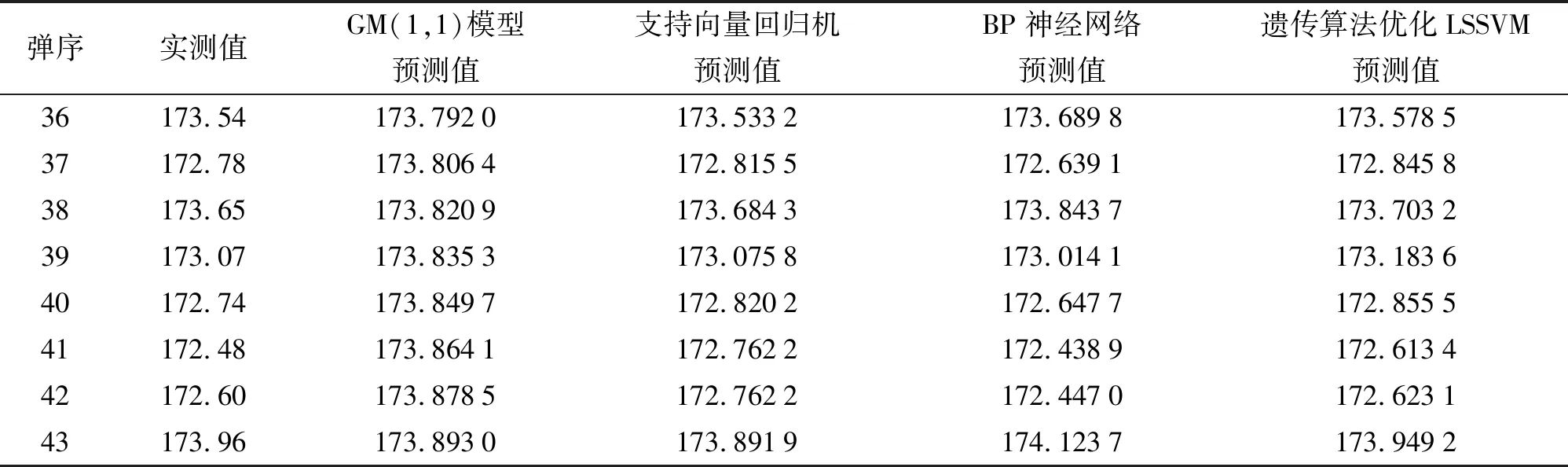
表5 雷达B(DATA2)第36～43发实测值与所有模型预测值 m·s-1

根据表5可以看出，除了GM(1,1)灰色模型的预测值与实测值相差较大以外，其余模型预测值都很接近实测值。经过详细计算得出：GM(1,1)灰色模型的预测值与实测值的平均相对误差为0.438%；支持向量回归机预测值与实测值的平均相对误差为0.049%；BP神经网络预测值与实测值的平均相对误差为0.071%；遗传算法优化LSSVM预测值与实测值的平均相对误差为0.040%，表明遗传算法优化LSSVM预测的初速数据误差最小，精度最高。此外，遗传算法优化LSSVM预测值与实测值的绝对误差均小于实测值乘以1‰的误差标准。

通过利用ARIMA模型、GM(1,1)模型、支持向量回归机、BP神经网络、遗传算法优化LSSVM对2组初速数据的建模预测结果可知，遗传算法优化LSSVM模型预测雷达B缺失的初速数据，不论是整体的预测精度还是单项预测精度都基本满足雷达测试弹丸初速的精度要求，预测出的数据是准确可信的，可以作为靶场试验中缺失初速数据的补充数据。

5 结束语

当雷达B的初速出现缺失时，选择把雷达A的数据作为输入、雷达B的初速作为输出，利用已测数据分别训练ARIMA模型、GM(1,1)模型、支持向量回归机、BP神经网络、遗传算法优化LSSVM，然后把雷达A的数据代入到所建模型，就能预测出雷达B缺失的初速。实验结果表明，遗传算法优化LSSVM预测雷达B初速的精度最高，预测误差满足初速雷达测试弹丸初速误差小于1‰的标准，可以作为弹丸初速的预测模型。