高等数学的课程思政教学设计——以“常数项级数”为例

汪小玉

(合肥师范学院 数学与统计学院 安徽 合肥 230601)

引言

高校课程思政建设，是落实立德树人根本任务的必然要求，也是全面提高人才培养质量的重要任务[1].而高等数学作为高校的一门基础课程，所占课时多，内容丰富，是实施课程思政的一门经典课程.本文以常数项级数相关概念的引入为例，挖掘其所蕴含的思政元素。

1 高等数学教学中实施课程思政的必要性

高等数学是一门充满了哲学和辩证法的课程.其中的概念、定理、性质包括例题都蕴含了丰富的哲理，将数学的理性思维、严谨推理、应用价值、文化内涵、美学元素更好地融入教学中，对学生三观的形成具有深远的影响.深刻理解课程思政的重大意义，深入挖掘高等数学课程内容及设计环节中所蕴含的思政元素，围绕育人目标，强化育人观念，构建多元化课程思政体系的教学实施方案，很有必要，迫在眉睫[2]。

2 高等数学课程思政教学设计的原则

教师需要坚定的政治立场，把提高学生的政治觉悟融入到课程中.在设计高等数学课程教学内容时，发挥自身及思政元素的导向性功能，积极弘扬名族精神和党的方针政策，保障学生在获得扎实的高等数学知识的同时，还能得到思想上的升华，感受到精神的洗礼，充分发挥教师的导向性作用。

教师在设计教学内容时应遵循自然性原则，将思政元素自然的融入教学过程中，不能让学生感觉内容的刻意生硬，要遵循自然性原则。

在情感性原则中，简单地把思政元素融入教学内容是不够的，教师注重对学生人文精神的熏陶.依据以学生为本的教学理念，为学生营造有真情实感体验的学习氛围，关注学生情感情绪的变化.通过沟通了解互动，增强学生情感需求，进而建立良好的师生关系，引导学生正确认知是非观念，使课程思政的教学效果更优质[2]。

3 常数项级数概念的课程思政教学设计

3.1 定义中的有限与无限的辩证统一

在高等数学“常数项级数的概念”这一内容的教学过程中，首先引入我国古代著名哲学家庄子在其著作《庄子·天下篇》中的名句“一尺之锤，日取其半，万世不竭.”[3]向学生解释这句话的基本含义是：一尺长的木棒，今天砍一半，明天砍一半的一半，每天这么砍一半，万世万代没有竭尽之时.木棒的长度是有限的，“日取其半”这件事是无限的，这包含了有限与无限辩证统一的思想，也体现了我国古代哲学家的智慧。

(1)

很自然地就有了无限个数求和的一个式子，从而进一步引发学生思考无限个实数之和什么时候存在。

紧接着引入常数项级数的定义，指出定义只是形式上的表达，还需要确切的数学解释；同时剖析常数项级数敛散性的概念，借助已知的“有限和”推广到“无限和”，并利用极限思想定义级数收敛和发散[4]。

3.2 例题中学以致用 增强信心

回到引例，公式(1)即可用级数收敛的定义验证.而仔细观察(1)式可知，构成(1)式的数列是一个等比数，所以自然地将其推广到一般的等比数列构成的级数的敛散性判断的例子。

例1 无穷级数

(2)

叫做等比级数(又称为几何级数)，其中a≠0，q叫做级数的公比.试讨论级数(2)的收敛性[5].

解 若q≠1，则部分和

当q=-1时，

sn=a-a+a-…-(-1)na,

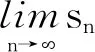
此例题结论应用性较强，而且等比数列求和，学生比较熟悉，解题过程容易理解，学生很容易接受新知识.为了巩固所学定义，可以再给出下面的例2,并且让学生先解答，老师再讲解。

解 级数的部分和

课堂上可以发现，例2 解题过程大部分学生会写，主要原因是此题前n项和的求解方法是“裂项相消”.给出此例题，一方面可以巩固常数项级数利用定义法判断收敛性，另一方面，可以让学生体会到利用旧知识能解决新问题的成就感，做到“学以致用”，无形中增强了学生学习高等数学的自信心[6]。

3.3 结论中的积少成多 量变到质变

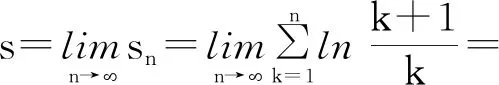
这一结果蕴含了丰富的育人之道.此时可以引导学生总结与结论相关的名句，比如“勿以善小而不为，勿以恶小而为之”，“不积跬步无以至千里，不积小流无以成江河”.同时想到习近平总书记所说的“每个人的生活都是一件件小事组成的，养小德才能成大德.”

让学生明白积少成多，由量变到质变的道理，在学习上，要每天积累，为将来人生的华丽蜕变打基础，在生活中，特别是当前疫情还未结束的情况下，做到“出门戴口罩，少聚集”等小事，就是为抗击疫情做了大贡献。

3.4 总结思考

①总结课程主要内容，布置作业；

②查阅资料：古希腊学者Zenot提出的“Achilles追赶乌龟”的悖论，从中体会有限与无限的关系[7]；

③思考问题：在学习和生活中，自己如何做，才能积少成多，提高自身的知识水平和解决问题的能力？不妨制定计划开始行动！

4 结语

本次常数项级数概念的教学设计，从古代经典实例出发，导出问题，引出概念，并应用于实际解决问题，帮助学生巩固知识，同时自然融入思政元素，达到教学与育人的双重功效.