稀土四硼化物表面性质的第一性原理研究

韩 星，王 健，何志军，邱东超

（辽宁科技大学 理学院，辽宁 鞍山 114051）

硼（B）原子具有多样化的结构和化学键，其缺电子特性能够形成强共价键或多中心键［1］。LaB6由于逸出功低、工作温度低及耐离子轰击等优点，成为热阴极材料领域的研究热点。研究表明［2］，对于电子发射材料，即使其电子功函数降低0.1 eV，也可能使器件性能显著改进。作为热阴极发射材料，除了较低的功函数外，还需要具有较高的熔化温度和为发射电子提供足够高的导电性。实验表明［3］，稀土四硼化物RB4族与六硼化物一样具有导电性和耐火性，可能是电子发射应用的前景材料。Deacon等［4］研究从La溶液中生长LaB4单晶的方法，并确定晶格参数、热膨胀系数和显微硬度及生长面，与LaB6的电子发射性能相当。Lazorenko等［5］研究单晶GdB6的发射时发现，对于任何含有可见GdB4包裹体的样品，发射都显著增加。这表明单晶GdB4具有较高的发射率。

电子发射是一种表面现象，作为理想的热阴极材料，重要特性是具有低功函数和高表面稳定性。对于LaB6的研究已经非常广泛，Uijttewaal等［6］基于密度泛函理论对LaB6的（001）、（011）、（111）、（112）和（012）表面的功函数和表面能进行理论计算。Schmidt等［3］研究金属六硼化物不同终端对功函数影响。相对来说，对于RB4表面性质的报道较少，更没有系统预测其功函数和表面能。

为进一步了解RB4的表面性质，更好地应用在电子发射领域，本文利用密度泛函理论（Density function theory，DFT）系统地研究RB4不同低米勒指数表面，即（001）、（110）、（100）的表面性质，探究表面能和功函数的内在联系，了解稀土四硼化物表面性质的变化趋势，为深入研究RB4理化学性质提供一种理论方法。

1 计算方法与模型

1.1 计算模型

RB4（R=La，Ce，Gd，Tb，Dy）属于四方晶系，空间群为P4/mbm［7］。图1为LaB4的单胞模型。为了详尽地描述其表面性质，本文选取（001）、（110）、（100）三个主要密排面。由于模型中最外层的原子排布和种类具有一定的随机性，以LaB4为例考虑不同终结面的情形，构建三个典型终结面块体模型：以La原子为终结面的（001）面，以B原子为终结面的（001）面，以La和B原子构成的混合终结面（110），如图2所示。其余模型与之类似。

1.2 研究方法

本文所有计算采用基于密度泛函理论的VASP（Vienna ab-initio simulation package）软件包中的PAW（Plane additive wave）方法［8］。电子交换关联能采用PBE（Perdew-Burke-Ernzerhof）广义梯度近似方法。采用周期性边界条件，片层之间的真空层厚度为1.5 nm，避免相邻表面的相互作用。K点网格根据表面模型的厚度选取，平面波的截断能是500 eV，真空层Z方向的K点基数为1。

1.3 电子功函数

功函数是自由电子脱离金属束缚所需要的最小能量。在0 K和绝对真空环境下可以表示为

式中：Evacuum为材料的真空能级；Efermi代表材料的费米能级。

不同材料的电子功函数不相同，即使是同一种材料的不同表面功函数值也千差万别。功函数反映材料的微观性质，尤其是对电子发射材料的功函数分析必不可少。基于第一性原理的功函数理论计算已经相对成熟，可以用来预测和分析材料的性质。

1.4 表面能

表面能反映材料的某个表面的稳定性。理论计算中，表面能是创造物质表面时，破坏分子间化学键所需消耗的能量。表面能越小，则表面的稳定性越好。化学计量比表面的表面能计算方法

式中：S是所选表面的面积；Eslab是优化后表面模型的总能量；Ebulk是材料单胞的能量；N是模型中总的原子个数。

对于非化学计量比的表面，需考虑表面模型中不同化学组分的影响。表面能计算需具体到每个原子的化学势，计算式为

式中：NB和NR是模型中B原子和稀土原子的个数是硼原子和稀土原子的化学势；PV和TS分别表示在一定状态下，表面能受压强和温度影响的值。在0 K时这两项可以忽略不计。经过结构弛豫后，在热力学平衡条件下，块材RB4和B及R的化学势关系

又因为RB4的化学势定义

由式（4）和式（5）得表面能的计算式

RB4中R和B原子的化学势应小于其块材的化学势。否则，所得片层模型由于其较高的化学势将会不稳定。因此，之间必须确保根据式（5）和式（6）得到RB4不同终端表面能对应于B原子的化学势范围为

2 计算结果和讨论

2.1 晶体结构优化

经过几何优化后，晶体结构完全弛豫，计算平衡晶格常数。表1列出RB4晶格常数的理论计算值与实验值。优化后得到的晶格常数a和c数值变化通常不明显，一般采用轴比a/c体现晶格常数变化大小。理论值与实验值吻合。

表1 RB4的晶格常数Tab.1 Lattice constants of RB4

2.2 四硼化物的电子功函数

2.2.1 对称模型的电子功函数 电子功函数具有各向异性，不同表面的功函数并不相同。以图2中（001）面B原子终结面及La原子终结面为例，采用上下表面对称的截取方式计算静电势能，结果如图3所示。真空能级与费米能级之差即为所求功函数，即φa=3.18 eV，φb=4.19 eV。在同一晶面（001）下，以La原子为终结面的功函数明显小于以B原子为终结面的表面功函数。这表明表面终结原子的种类直接影响材料的表面性质。

图4给出RB4（001）表面和（110）表面不同终结面的功函数计算结果。模型仍采用上下对称截取方式。结果表明，以R为终结面的表面功函数明显小于以B为终结面的功函数。此结果与Uijttewaal等［6］的结论一致。在各个表面功函数的计算结果中，（110）面以B和R混合终结面的功函数最小，其中LaB4的功函数只有2.487 eV，与主流热阴极发射材料LaB6的功函数（2.66～3.4 eV）［6］相当，甚至优于LaB6，这使得LaB4的应用成为可能。RB4功函数的理论值随着R原子序数的增大而增大，各个表面功函数变化的范围变小，尤其是从Gd到Dy RB4的功函数基本持平。

2.2.2 非对称模型的功函数 图5是（100）面的非对称模型，采取偶极矩矫正的方法计算模型上下表面的功函数，结果列于表2中。以LaB4的（100）面为例，计算其静电势能曲线，如图6所示。

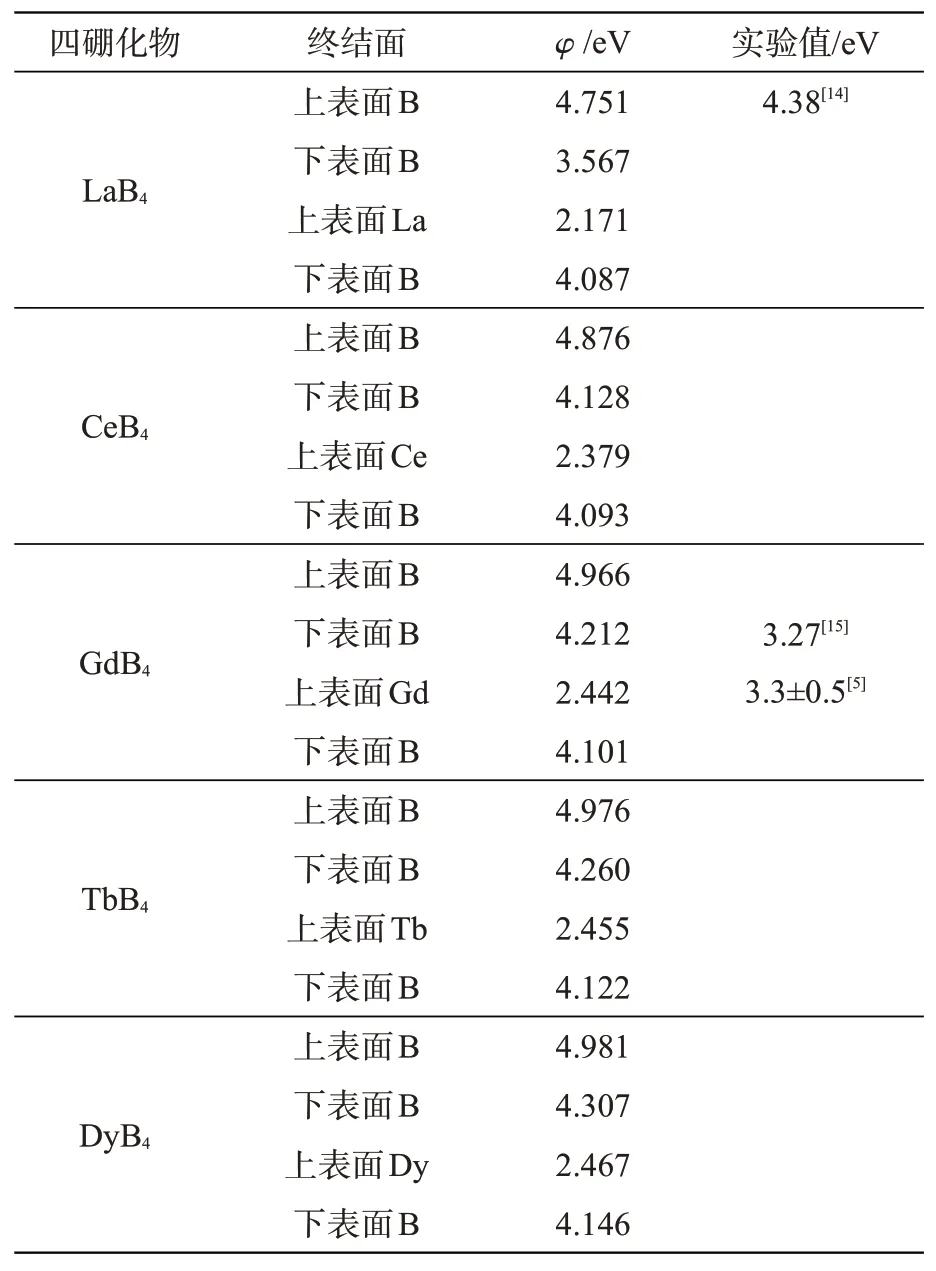
表2 RB4（100）面不同终结面的功函数Tab.2 Work functions of different RB4（100）end surfaces

在图6中，非对称表面的静电势在施加偶极修正后的真空区表现出一个“势跃”，左侧是以La为终结面的功函数，右侧是以B为终结面的功函数。这个“势跃”抵消了由周期性边界条件引起的偶极矩。表2中，同一晶面不同终结面的功函数有差异，这与模型的表面原子排布有关。总体而言，以R原子为终结面的功函数明显小于以B原子为终结面的表面功函数。计算结果与实验数据吻合。功函数大小存在以下关系：φ(DyB4)＞φ(TbB4)＞φ(GdB4)＞φ(CeB4)＞φ(LaB4)。在RB4模型中，以（100）面的LaB4的功函数最低，达到2.171 eV，性能最优异。

2.3 表面能

表面能γ是劈裂体相晶体所需的能量，其本质就是把切断过程所需的能量等效为新形成两个表面所需的能量。表面能直接反映材料表面的稳定性。

由于选取的片层模型是上下对称的，因此其化学组分是非化学计量比。根据式（7）绘制出LaB4的不同晶面不同终端对应于B原子化学势的关系曲线，如图7所示。在LaB4（110）表面B原子化学势低的范围内（-0.6～-1.4 eV），B终端的表面能比La终端的表面能高，当B原子化学势增大至0.6 eV以上时，La终端的表面能变大，而B终端的表面能越来越小。但是从总体来看，以La为终端的表面在-0.6～-1.4 eV的较大范围内表面能较高，因此结构不太稳定，即LaB4（110）面B终端的表面比La终端的表面具有更高的热力学稳定性。而在LaB4（001）表面，在化学势0～0.8 eV的较大范围内，以La为终端的表面能比B终端表面能高。在B原子化学势低的范围（-0.8～-1.4 eV）内，混合终端表面能相较于其他两种终端的表面能最低。以B为终端的表面能随化学势的增大而减小，表明B终端表面逐渐趋于稳定。

其他四种RB4的不同终端表面能与B化学势之间的关系曲线如图8所示。不同终端的表面能随B化学势的变化而不同。但五种RB4的表面能有相同的变化趋势。例如，（001）-B和（110）-B的表面能随B化学势的增大而减小，而R终端和混合终端变化趋势则相反。这表明随着B化学势的增加，B终端的表面趋于稳定。在整个B化学势的范围内，（001）表面能的变化幅度大于（110）表面。

非对称模型RB4（100）的表面能变化趋势如图9所示。表面能与功函数的计算结果趋势一致。随着原子序数的增加，表面能增加。B终端的表面能明显大于R终端的表面能，表明以稀土金属R为终端的表面最稳定。

3 结论

本文采用基于密度泛函理论的第一性原理方法计算RB4（R为稀土金属La，Ce，Gd，Tb，Dy）的表面能和功函数。RB4不同晶面功函数变化规律：φ(001)-B＞φ(001)-R＞φ(110)-R＞φ(110)-混合终结面。功函数的大小与原子序数也密切相关，φ(DyB4)＞φ(TbB4)＞φ(GdB4)＞φ(CeB4)＞φ(LaB4)。对于化学计量比和非化学计量比表面，R端的表面能和功函数都低于B端。五种RB4中，LaB4的功函数最低，可达到2.171 eV，是一种理想的电子发射材料。