基于声振耦合的曲面微穿孔板吸声特性研究及试验分析
2022-10-27张永锋李国防倪俊芳孔德瑜盛哲昊
张永锋, 李国防, 王 刚, 倪俊芳, 孔德瑜, 盛哲昊
(苏州大学 机电工程学院,江苏 苏州 215131)
微穿孔板模型被广泛应用于吸声降噪领域,其吸声理论最早由Ma等[1-5]提出并进行不断完善的。基于微穿孔板吸声理论,许多学者和研究人员针对如何提高微穿孔板吸声性能问题做了大量工作。Lee等[6]研究了带有声腔的柔性微穿孔板吸声,得出面板振动效应可以耗散更多能量,相应的吸收峰可以加宽穿孔板的吸声带宽;侯九霄等[7]在考虑弹性背腔振动下,研究了弹性微穿孔板与背腔的耦合情况;Bravo等[8]研究了薄板振动对微穿孔板吸声性能的影响,建立了微穿孔板于背腔耦合模型。为了进一步拓宽吸声带宽,解决单层微穿孔板吸声峰单一的问题,多层微穿孔板结构被提出[9]。Cedric等[10]建立单层和多层微穿孔板吸声结构,提出了一种全耦合模态方法来计算其吸收系数和传输损耗。
前述研究均为平面板,曲面微穿孔板是将平面微穿孔板设计为曲面结构,使之更适于在墙壁转角等场合。因此对曲面微穿孔板的吸声性能的研究具有一定的理论意义和工程应用前景。Jin等[11]用基于一阶剪切变形理论的改进的傅里叶法,研究了在任意边界条件下功能梯度材料双曲面壳体的振动。Ventsel等[12]提出了薄板和壳体的理论分析与应用。Szechenyi[13]提出了确定加筋板和弯曲板的固有频率的近似方法。Lee等[14]研究了空气腔支撑的柔性弯曲微穿孔板的吸声性能,建立了一个基于经典平板方程和声波方程耦合的理论模型,用于预测吸声量。
在实际应用中根据不同的需求,不同的墙壁转角处的环境对曲面微穿孔板进行设计,对比其他的吸声材料和吸声结构,曲面微穿孔板有着质量轻,工艺要求低,成本低,易于加工等优势。前述文章对考虑板的振动时微穿孔板吸声性能的影响进行了研究,本文针对简支边界和固支边界条件下,同时考虑板的振动时,探究了各种参数对曲面微穿孔板的影响规律。
1 理论模型
1.1 曲面微穿孔板吸声系数求解
曲面微穿孔板吸声结构如图1所示,曲面微穿孔板设置在墙壁上,曲面微穿孔板与墙壁组成的背腔结构构成曲面微穿孔板吸声装置。设墙壁为刚性壁面,微穿孔板采用弹性材料制成,微穿孔板到其背后的墙壁的距离D取平均值,P为板表面声压。
结合声电类比法,其等效电路图如图2所示。
图2中:ZD为背腔的声阻抗;Ro和Io分别为微孔的声阻抗Zhole的实部和虚部;Rp和Ip分别为曲面微穿孔板的声阻抗Zmn的实部和虚部。
板的模态阻抗和微孔的声阻抗可以看作并联结构,根据其等效电路图可以整个吸声系统的声阻抗Z,如式(1)所示
(1)
从而得出曲面微穿孔板的吸声系数
(2)
式中:Re(Z)为声阻抗Z的实部,表示为声阻;Im(Z)为声阻抗Z的虚部,表示为声抗。
图3为曲板结构示意图,其中R为曲板的曲率半径,u,v,w分别为板在x,y,z三个方向的振动位移,a为板的长度,b为曲面一边的弧长,α为曲面弧长对应的角度,φ为从y=0开始沿弧长b转过的角度。
根据Love理论[15],板在每个振动单元的势能为
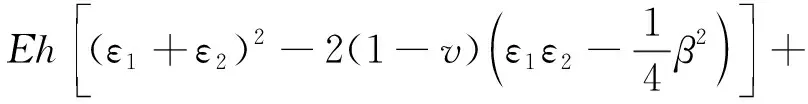
式中:E为板的杨氏模量,Pa;h为板厚,m;v为泊松比,其中ε1,ε2,K1,K2,β,τ表达式分别为
(4)
板在每个振动单元的动能为
(5)
式中,ρp为板的面积密度,然后根据Rayleigh法得到如下等式
[∬Udxdy]max-[∬Tdxdy]max=0
(6)
如果已知所有三个坐标方向的精确振型函数,则可求得模态固有频率的解,对于简支边界,三个方向的振型函数可设为
(7)
把式(3)、式(5)和式(7)代入式(6)中,即可得到系数A,B,C以及曲面板的固有频率为ωmn

对于固支边界可设三个方向的振型函数为
式中:γ=m+1/2;ε=n+1/2。
同样地,可得到三个方向上振型函数的系数A,B,C以及固支边界下曲面板的固有频率ωmn
(10)
式中:Pm=1-2/πγ;Pn=1-2/πε。
则板的声阻抗Zmn可根据模态叠加法[15]由式(11)求出
(11)
式中:ρp,ξmn,ωmn分别为板的面积密度、板的模态阻尼系数、板的第(m,n)阶固有频率,脚标m,n分别对应的是x方向和y方向上的波数。
背腔的声阻抗ZD,其值按式(12)计算
ZD=-jρ0c0ctg(ωD/c0)
(12)
式中:ρ0为空气密度(1.2 kg/m3);c0为声波在空气中的传播速度(340 m/s);ω为声压P的圆频率;j为虚数单位,j2=-1。
微孔声阻抗Zhole可由马氏理论[16]求出,其值按式(13)计算
(13)
其中,
(14)
相对声阻r为
(15)
相对声质量m为
(16)
声阻常数kr为
(17)
声质量常数km为
(18)
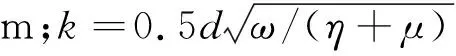
(19)
式中,e为孔间距,m。
1.2 考虑板振动时的吸声系数
如图4所示为在固支边界下考虑板的模态阻抗与忽略板的模态阻抗影响的吸声系数对比,板的参数为a=0.15 m,b=0.15 m,板厚h=2 mm,孔径d=0.8 mm,穿孔率σ为2%,曲率半径R=2 m,背腔深度D=0.2 m。
从图4中可以看出,在考虑板的模态阻抗的情况下,微穿孔板吸声系数在474 Hz处会出现一个峰值,这是由板的共振引起的(此时板的第一阶模态ω11=2π×473.95 rad/s,模态阻尼系数ξ11=0.02),并且由板的共振引起的吸声峰值比微孔引起的吸声峰值更高,结合两者可以有效的拓宽此吸声系统的吸声带宽。
1.3 各参数对曲面微穿孔板吸声性能的影响
1.3.1 穿孔率对曲板吸声性能的影响
取a=0.2 m,b=0.2 m,板厚h=2 mm,孔径d为0.6 mm,曲率半径R=2 m,背腔深度D为0.2 m,在简支边界和固支边界下,不同穿孔率的吸声系数和声阻抗分别如图5和图6所示。从图5和6可以看出,随着穿孔率的增大,无论是固支还是简支边界,声阻和声抗都呈减小的趋势,单纯考虑穿孔率对吸声系数的影响时,在本文取值范围内穿孔率越小,最大吸声系数越大,最大吸声系数所在位置(共振频率)向高频移动,吸声带宽增大,在此参数下固支边界吸声带宽增加更加明显。声阻出现的峰值位置和吸声系数出现峰值位置一致,且在此处声阻明显增大,而声抗在此处的变化幅度不如声阻,但整体随频率变化而增大的幅度比声阻较大,由此可见声阻对吸声的峰值有重要贡献。
1.3.2 孔径对曲板吸声性能的影响
保持穿孔率σ为3%,板厚h为2 mm,曲率半径R为2 m,背腔深度D为0.2 m,在简支边界和固支边界下不同孔径对应的吸声系数和声阻抗分别如图7和图8所示。从图7和图8可以看出,随着孔径增大,无论是固支还是简支边界其整体声阻都有所下降,而整体声抗则变化较小,整体声阻随着频率的变化会出现峰值(d=0.6 mm ∶简支313 Hz,固支433 Hz),而整体声抗则在整体上呈增加趋势。随着孔径增大,由于板的振动引起的吸声峰值位置不变(简支317 Hz处,固支440 Hz处),由于微孔引起的吸声峰值下降,而吸声系数峰值与声阻抗峰值位置略有差异,这是由于声抗的作用引起的。可以通过减小孔径的方式来增大吸声系数和拓宽吸声带宽。在使用中,灰尘等颗粒物的污染会堵塞微孔,影响吸声性能,因此必须保持微穿孔板表面清洁。
1.3.3 板厚对曲板吸声性能的影响
保持穿孔率σ为3%,孔径d=0.6 mm,曲率半径R=2 m,背腔深度D=0.2 m,在简支边界和固支边界下不同板厚下的吸声系数和声阻抗分别如图9和图10所示。从图9和图10可以看出,随着板厚的增加,板的整体声阻峰值变大且向高频移动,整体声抗变大。随着频率的变化,声阻除出现峰值外,整体变化较小,声抗呈增加的趋势,单纯考虑板厚对吸声系数的影响时,在本文取值范围内,板厚越大,由于板的共振引起的吸声峰值向高频移动,其吸声系数明显下降,而由于微孔引起的吸声峰值变化较小。另外,增加板的厚度,声阻的峰值变大,而吸声系数的峰值却并没有随之增大,因此在保持相应的吸声性能时,板厚不宜过大。
1.3.4 曲率半径对曲板吸声性能的影响
保持穿孔率σ为3%,孔径d=0.6 mm,板厚h为2 mm,背腔深度D为0.2 m,在简支边界和固支边界下不同曲率半径下的吸声系数和声阻抗分别如图11和图12所示。随着曲率半径的增大,无论是固支还是简支边界其声阻峰值逐渐变小,当曲率半径大于2 m时,声阻和声抗变化都较小,这是因为曲率半径足够大时,曲面板逐渐接近平面板,对于声阻抗的影响逐渐减弱。随着频率的变化,声阻的峰值向低频移动,吸声系数的变化趋势与声阻抗相吻合,但其吸声系数最大值随着曲率半径的变化较小,吸声频带变窄。
1.3.5 背腔深度对曲板吸声性能的影响
保持穿孔率σ为3%,孔径d=0.6 mm,板厚h为2 mm,曲率半径R为2 m,在简支边界和固支边界下不同曲率半径下的吸声系数分别如图13(a)和图13(b)所示。从图13可知,随着背腔深度的增加,由微孔引起的吸声峰值向低频移动。根据式(12)可以看出,背腔深度的变化不会对微穿孔板的声阻产生影响,声腔的作用主要是调节微穿孔板结构的共振频率。
1.3.6a与b的比值对曲板吸声性能的影响
取穿孔率σ为2%,孔径d=0.6 mm,板厚h为2 mm,曲率半径R为2 m,在简支边界和固支边界下不同a/b值的吸声系数,如图14所示。从图14可以看出,随着a/b的增加,由于板的振动造成的吸声峰值逐渐向高频移动(简支边界:284 Hz;317 Hz;354 Hz;431 Hz;固支边界:405 Hz;444 Hz;498 Hz;628 Hz);由于未改变整体穿孔率板厚以及孔径等参数,由于微孔引起的吸声峰值变化较小。
2 试验与分析
2.1 试验原理及装置
本次试验采用的是阻抗管法进行测量单曲面微穿孔板的吸声系数。本文试验测试系统流程如图15所示,阻抗管的一端为扬声器,另一端为被测材料,扬声器通过数据采集前端产生的白噪音信号经过功率放大器驱动产生声波,在靠近待测材料处放置两个传声器来测量两个位置的入射声压和反射声压,利用传递函数法求得垂直入射时的材料吸声系数和声阻抗。
本文设计阻抗管管径d1为100 mm的方形管,管长350 mm,采用亚克力材料制造。取两传声器之间的距离s为200 mm,根据标准ISO 10534-2:1988(E)可以得到阻抗管的测量频率的上下限为(fl为工作下限;fu为工作上限)
(20)
(21)
根据标准进行设计后,最终搭建试验平台如图16所示。阻抗管法测量材料吸声系数属于声强测量,通过两个传声器测得的声压信号间接求出声强,传声器相位失配误差难免会对测量有所影响,为此应采取适当措施修正相位失配误差。
本文采用的是预先测定标准因数的方式来进行传声器失配的矫正。校准后对后续测量都有效,对于样品的多次测量比较方便。
(22)
式中,m为传声器传递函数。为了后续测量,再将传感器按方式Ⅰ布置,测得传递函数H12为
H12=GaGm=|Ga||Gm|∠(φa+φm)
(23)
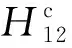
(24)
2.2 试验结果
取穿孔率σ=1.5%和σ=2.5%的曲面微穿孔板,如图19所示。
板的参数为:a=0.1 m,b=0.1 m,孔径d=0.7 mm,板厚h=1 mm,曲率半径R=0.15 m,试验测得的吸声系数曲线和理论计算结果如图20所示。由图20可知,随着频率的增加,穿孔率σ=1.5%时理论计算结果和试验结果均存在两个峰值(理论结果635 Hz,897 Hz;试验结果742 Hz,890 Hz),由于微孔引起的吸声峰值位置有些差异,由于板的共振引起的吸声峰值基本一致,而穿孔率σ=2.5%时理论计算结果和试验结果均存在一个峰值(理论结果878 Hz;试验结果875 Hz),这是因为由于微孔引起的峰值位置与板的共振频率非常接近导致由于微孔引起的峰值并未明显显示。由于试验模型是独立根据标准设计并加工,在密封性和板的安装边界条件上,不能与理论计算模型一模一样,但从结果看,整体变化趋势趋于一致,验证了在一定范围内随着穿孔率的不断增大,吸声由于微孔引起的吸声峰值下降,整体吸声带宽变小。
3 结 论
本文基于微穿孔板理论结合板的振动采用声电类比法获得了曲面微穿孔板的吸声系数,并进行了参数分析。设计了阻抗管测量装置,并采用阻抗管法对曲面微穿孔板进行了吸声系数测量,把理论计算结果与试验测量结果进行了对比,验证了理论分析的准确性。本文主要完成了以下几方面内容:
(1)建立曲面微穿孔板数学模型,求解出固有频率,并利用声电类比法,得到曲面微穿孔板的吸声系数;对于不同边界下,分析了各参数对曲面板吸声系数和声阻抗的影响规律,其中穿孔率和孔径对曲面板吸声性能影响最大。
(2)为了验证理论模型的准确性设计了阻抗管装置,测量了微穿孔板的吸声系数,对比分析了微穿孔板的理论值和试验值;对不同穿孔率下的吸声系数进行了测量,结果表明,随着穿孔率和孔径的增大,由微孔引起的吸收峰值下降,整体吸收带宽减小。
