金属橡胶/碟簧叠层复合结构阻尼特性及其非对称迟滞模型参数识别

吴乙万， 程 湖， 白鸿柏， 訾 宝， 汤 宇

(福州大学 机械工程及自动化学院 金属橡胶与振动噪声研究所，福州 350108)

碟形弹簧(以下简称碟簧)是由钢板冲压成形的碟状垫圈式弹簧，其具有体积小、储能大、组合使用方便等优良特性[1-2]。一方面，通过改变碟簧的数量、组合形式(串联、并联、复合)可获得不同的载荷特性；另一方面，碟簧片间存在锥面摩擦及边缘摩擦，在往复荷载作用下具有一定的耗能能力。碟簧已被广泛应用于国防、冶金、机床、建筑、生物医学等多个行业[3-5]。肖舒恒等[6]对碟簧螺栓连接结构受阶跃冲击载荷响应进行研究，结果表明，其结构能有效降低螺栓峰值应力，且能迅速衰减冲击产生的振动。都军民等[7]分析了碟簧减振系统的动态特性，建立单向约束条件下的动力学方程，并研究非线性阻尼特性对动态特性的影响。

为了提高碟簧及其组合件的阻尼性能，一些学者基于材料或结构做了大量研究工作，如在碟簧隔振缓冲装置中设置黏弹性阻尼层，构成碟簧复合隔振装置。王维等[8]利用碟簧隔震支座与黏弹性阻尼材料相结合，研究了加载预压量、位移幅值和加载频率对其力学性能的影响，结果表明，黏弹性阻尼材料能够有效提高复合结构的耗能能力。Jia等[9]研究了添加聚氨酯片(PU)前后碟形弹簧的力学性能,试验结果表明，PU能够在保持碟簧静刚度基本不变的同时，降低其动刚度，在相同冲击力作用下，复合结构存在一个最佳的阻尼比。

金属橡胶(entangled metallic wire materials,EMWM)是一种由各种牌号细金属丝经特定工艺制备的弹性阻尼多孔材料[10]。通过选择合适的丝材制备金属橡胶满足各种恶劣应用环境下设备的隔振缓冲需求。金属橡胶的耗能机理：在外部载荷作用下，金属橡胶发生变形，其内部相互接触的金属丝发生滑移摩擦，进而将振动能量转化成热能进行能量耗散。将金属橡胶应用在高温和大振幅下的转子支架[11]、管路[12]、高速铁路[13]，仍能够保持良好的阻尼性能。

虽然已有的研究表明将碟簧与阻尼材料进行结合形成复合缓冲结构可提高碟簧组的耗能水平，但复合结构所用的阻尼材料均为高分子材料，在一些恶劣的应用环境下(高/低温、腐蚀)高分子材料将加速老化、性能急剧下降甚至失效。这限制了碟簧缓冲结构的使用温度范围。

本文提出将金属橡胶与碟簧串联构成金属橡胶/碟簧复合叠层结构，以提高不同环境温度下碟簧缓冲结构的阻尼性能。采用正弦力激励法对金属橡胶/碟簧复合叠层结构进行系列化动态压缩试验，研究了叠层复合结构在不同激励条件和不同金属橡胶密度下的变化规律。结合试验结果与理论分析，基于迹法等效阻尼模型，考虑弹性恢复力和阻尼力随变形幅值、频率的变化规律，用参数分解识别法建立该叠层结构在一定载荷下的非对称迟滞模型。结果表明，参数识别精度能够满足工程应用的要求。本文研究对在额定载荷下非对称减振结构的应用设计有重要意义。

1 金属橡胶/碟簧复合叠层结构与试验方法

1.1 金属橡胶/碟簧复合叠层结构

本文提出的金属橡胶/碟簧叠层结构由两片碟簧与金属橡胶夹芯层共同组成，如图1所示。该结构通过金属橡胶内部螺旋线匝在接触点滑移摩擦以及其表层螺旋线匝与碟簧锥面的滑移摩擦来吸收冲击振动能量，通过金属橡胶与碟簧的弹性变形满足变形需求。

选用中国江苏省扬州市弹簧有限公司制造的碟簧(GB/T 1972—2005)，其材料为60Si2MnA，具体参数如表1所示。

表1 B系列碟簧参数Tab.1 Parameters of B-serial disc springs

采用文献[14]提出的四步法制备碟簧状金属橡胶，成型外径为140 mm，内径为72 mm，厚度为20 mm。如表2所示，不同密度的成型压力从20～47 kN内递增。将选用的碟簧与制备的金属橡胶夹芯层进行串联即可完成复合叠层结构样品的试制，如图1所示。

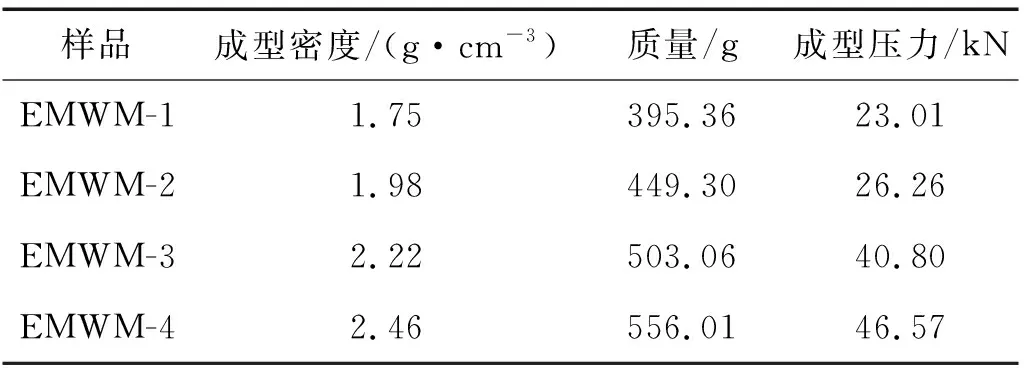
表2 金属橡胶夹芯层的制造参数Tab.2 Manufacturing parameters of EMWM layer

1.2 试验设备与方法

为探究不同激励条件和不同制备工艺参数对EMWM/DS动态阻尼性能的影响规律， 试验设备采用长春机械科学研究所SDS-200高低温动静万能试验机及测试工装如图2所示。其主要由水冷箱、液压站、控制面板、主机以及EDC控制器等组成。试验机最大工作载荷为200 kN，夹头最大行程±50 mm，加载频率范围为0.01～40 Hz。按照GB/T 15168—2013分别研究了不同结构、压缩量、频率、幅值、金属橡胶夹芯层密度对EMWM/DS的动态阻尼特性的影响。具体试验参数如表3所示。

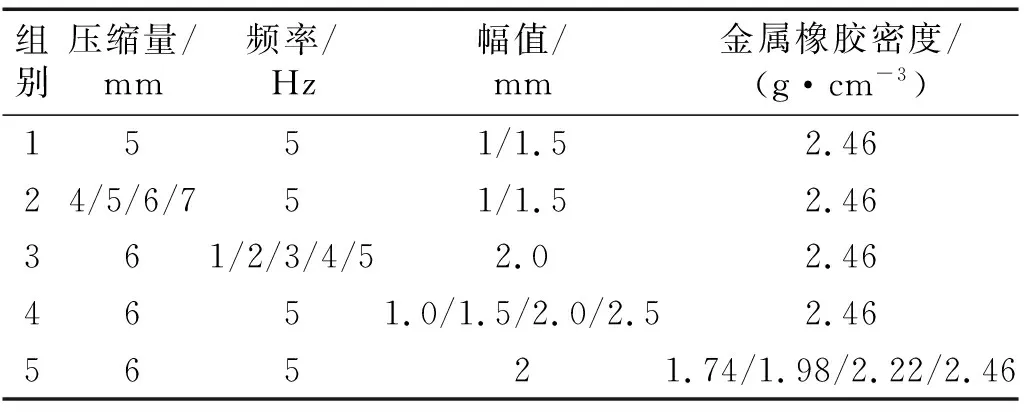
表3 单因素控制试验参数Tab.3 Single factor control test parameters

1.3 动态性能表征方法

采用正弦力激励法对金属橡胶/碟簧叠层结构(EMWM/DS)进行测试，将试验样件置于测试系统中以不同频率的正弦力激励，通过传感器采集恢复力与位移响应信号，通过数据分析计算一个周期内的耗能ΔW与最大弹性势能W，损耗因子η以及动态平均刚度k作为EMWM/DS的表征参量。如图3所示，恢复力包络的迟滞回线面积ΔW代表结构一个周期内绝对耗能，W则代表阻尼结构的最大弹性势能，损耗因子η表征复合结构阻尼性能。

动态试验机对复合阻尼结构的位移激励离散值可表示[15]为

(1)

式中:Y0为位移幅值；N=f0/f，f0为采样频率，f0=5 000 Hz，f为加载频率；α为初试相位。

复合阻尼结构在一个振动周期内损耗的能量ΔW，即迟滞回线的面积为

(2)

根据图3的数据处理流程，可求出F1(yj),F2(yk)，进而，最大弹性势能W可表示为

(3)

由式(2)、式(3)，可计算损耗因子

(4)

动态平均刚度可表示为

(5)

2 试验结果与分析

2.1 不同叠层结构的动态阻尼特性

根据表3中试验组别1的参数，可得到如图4所示的金属橡胶(EMWM-4)与复合叠层结构(EMWM/DS-4)的迟滞回线。多片碟簧叠合使用时主要通过碟簧片之间相互摩擦来耗能[16]，而金属橡胶在受载时，其内部金属丝发生滑移、挤压接触等方式的干摩擦。

由表4可知，复合叠层结构与金属橡胶的耗能和损耗因子相差不大，刚度有明显下降，这表明添加金属橡胶夹芯层可以有效增加碟簧阻尼结构的耗能特性。复合结构中的碟簧与金属橡胶夹芯层为串联关系，在变形幅值相同的情况下，碟簧产生部分变形，金属橡胶夹芯层则产生另一部分的变形，即金属橡胶夹芯层的变形量较金属橡胶(EMWM-2)的变形量小导致耗能ΔW和损耗因子η相对较小，而串联结构的总刚度k相对较低。

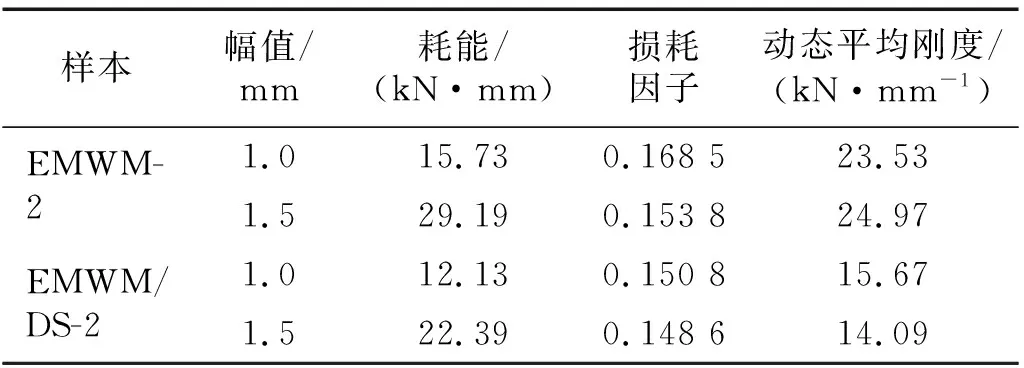
表4 金属橡胶与复合结构的动态阻尼特性Tab.4 Dynamic damping characteristics of EMWM and EMWM/DS

2.2 预紧量对复合叠层结构耗能特性影响

复合叠层结构具有明显的非线性阻尼特性，在不同承载作用下会发生不同的初始变形，即对应不同的预紧量。如图5所示，随着预紧量的增加，复合叠层结构的动态恢复力F逐渐上升。复合叠层结构中的金属橡胶夹芯层和碟簧都进一步受到压缩，金属橡胶内部金属丝之间的相互接触的螺旋卷得到更充分的摩擦，结合表5可看出，耗能ΔW、最大弹性势能W和动态平均刚度k均有增加的趋势；根据式(4)可知，当耗能ΔW的增速小于最大弹性势能W的增速时，损耗因子η随着预紧量增大而减小，反之则增大，因此损耗因子η呈波动性变化。

幅值/mm预紧量/mm耗能/(kN·mm)损耗因子动态平均刚度/(kN·mm-1)1.01.549.790.196 510.83512.130.150 815.67617.210.153 320.79721.940.161 824.54418.100.188 810.06522.390.148 614.09630.410.143 218.37737.240.145 721.17

2.3 频率对复合叠层结构耗能特性影响

图6可反映出复合叠层结构的迟滞回线受频率影响较小，结合表6可知，频率在1～5 Hz内变化对复合叠层的耗能ΔW和损耗因子η有着小幅度的变化。

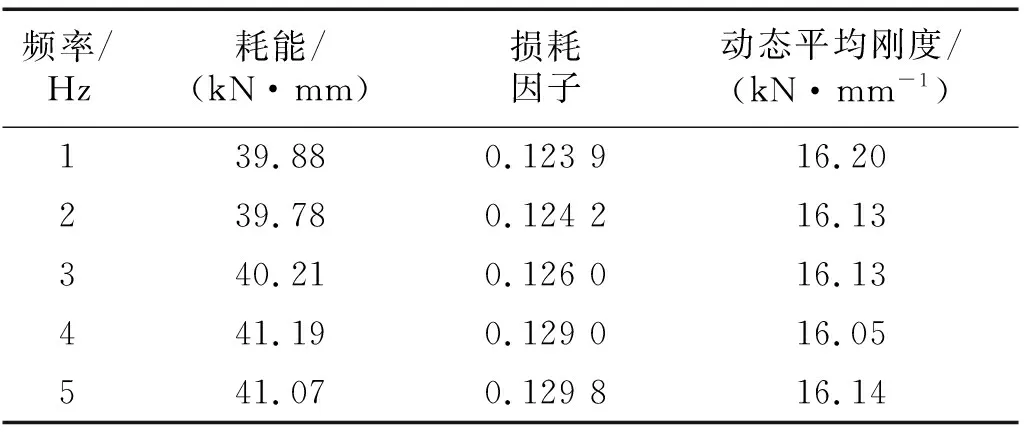
表6 不同频率下复合叠层结构的动态阻尼特性Tab.6 Dynamic damping characteristics of EMWM/DS under different frequencies

2.4 振幅对复合叠层结构耗能特性影响

如图7所示，随着振幅的增加，复合叠层结构的滞回面积不断增加，对应的耗能能力增加，这是由于振幅的增加，使金属橡胶内部金属丝在一个周期内经历滑动、挤压接触等形式的干摩擦增多导致的。由表7可看出，损耗因子和动态平均刚度随着振幅的增加而减小，振幅的增加导致复合叠层结构最大弹性势能W的增量大于金属橡胶耗能ΔW的增量，从而，复合叠层结构的损耗因子η逐渐下降。

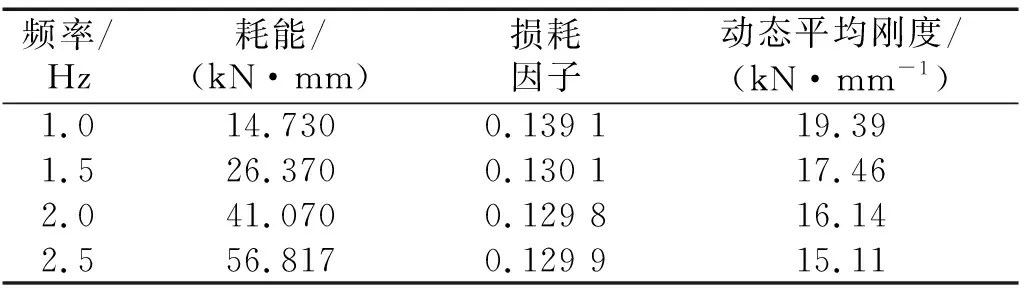
表7 不同振幅下复合叠层结构的动态阻尼特性Tab.7 Dynamic damping characteristics of EMWM/DS at different amplitudes

2.5 夹芯密度对复合叠层结构耗能特性影响

由图8可看出，随着金属橡胶夹芯层密度的增加，复合叠层结构的动态恢复力逐渐上升，其迟滞回线面积也明显增加。随着密度的增加，在相同位移幅值下，单位体积金属橡胶内部金属螺旋卷(看作小曲梁)接触点增加，小曲梁受到更多约束。从而，小曲梁AB等效长度越短，其刚度越大，导致总刚度(可等效为所有小曲梁刚度的叠加)增加，即动态平均刚度k增加。同时，金属线匝的接触点数量增多，滑动摩擦力增大(如图9所示，密度越大的金属橡胶对碟簧摩擦痕迹越明显)，使耗能ΔW、最大弹性势能W均增加。而耗能ΔW的增速小于最大弹性势能W的增速，损耗因子η随着密度增大而减小。

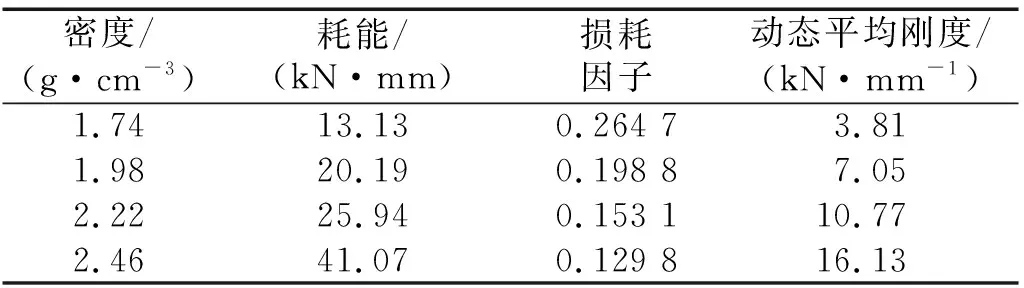
表8 不同夹芯层密度下复合叠层结构的动态阻尼特性Tab.8 Dynamic damping characteristics of EMWM/DS with different EMWM densities

3 非对称迟滞动力学模型及参数识别

3.1 非对称动力学模型

Ni等[17]提出了一种用于描述非对称迟滞曲线的数学模型，并给出了参数识别方法。吴善跃等[18]采用该方法建立数学模型时，发现计算过程中出现病态矩阵，提出了不含时间信息的非对称迟滞模型对其改进。以上方法均采用了Bouc-Wen迟滞模型，其通用性强，精度较高，但是各参数之间的关系很不直观，物理意义不明确。进而，周相荣等[19]引入混合阻尼因子简化了该模型。

根据图10所示，迟滞回线可以分为上、下半支，分别对应速度大于零和速度小于零的部分。采用幂函数对其迟滞回线进行多项式拟合，即上、下半支滞回线可表示为

(6)

(7)

将式(6)、式(7)中的幂级数多项式的奇、偶次项分开写，并统一写为

(8)

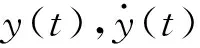
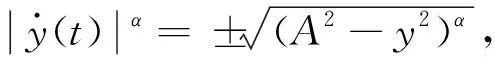
式中:k1,k3,k5分别为线性、三次、五次刚度系数;c为等效黏性阻尼系数;α为阻尼成分因子。

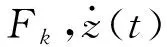
h(A)

(10a)

F1a(y(t))=k1(A)y(t)+k3(A)y3(t)+k5(A)y5(t)(10b)

F2a(y(t))=eb(A)y(t)

(10c)

(10d)

式中：b(A)为迟滞回线非对称参数;h(A)为迟滞回线中心偏移参数;A为变形幅值;f为变形频率。

为了避免计算过程中产生病态，本文采用吴善跃等研究中的参数分解识别方法进行参数识别。

3.2 参数识别过程

从第二章中的动态试验数据中提取某个工况下的位移与其对应的恢复力采样数据(yi,F(i),i=1,2,…,N)，通过两次坐标变换(如图11(a)、图11(b)所示)分别得到参数h,b随位移幅值变化的规律，而频率变化对其几乎没有影响。

(11)

(12)

根据式(13)中奇数项系数为待识别的刚度系数，即得到非线性弹性恢复力为

(14)

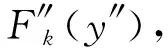
(15)

对式(15)进行参数识别即可得到等效黏性阻尼系数c及阻尼成分因子α。

迟滞回线中心偏移参数h(A)、非对称参数b(A)随变形振幅A的变化关系可表示为

h(A)=-0.127 6×A3+0.676 4×A2-1.186×A+

3.735

(16)

b(A)=0.438 1×A-0.241 4

(17)

线性刚度k1(A)、三次刚度k3(A)、五次刚度系数k5(A)随变形振幅A的变化关系可表示为

k1(A)=-0.269 8×A3+1.772×A2-4.112×A+

5.637

(18)

k3(A)=-0.362 6×A-2.755+0.042 75

(19)

k5(A)=1.355×A-4.822

(20)

等效黏性阻尼系数c(A,f)，阻尼成分因子α(A,f)为

c(A,f)=(-1.479×A3+7.832×A2-13.73×A+

8.893)×f-0.014 29

(21)

α(A,f)=-1.492+6.939A-0.129 4f-6.709A2+

0.790 1Af-0.112 6f2+2.876A3-0.414 1A2f-

6.893×10-2Af2+3.328×10-2f3-0.447A4+

8.083×10-2A3f-9.752×10-4A2f2+

8.862×10-3Af3-3.67×10-3f4

(22)

3.3 模型验证

将参数识别所得到的表达式(16)～式(22)代入式(10)中，即可得到EMWM-DS复合叠层结构的非对称动力学模型。为了验证所建非对称迟滞动力学模型及参数识别方法的有效性，应用非对称迟滞动力学模型预估不同工况(A,f)下的恢复力迟滞回线，金属橡胶/碟簧复合叠层结构EMWM/DS-1的试验实测数据与预估曲线进行对比如图12所示。

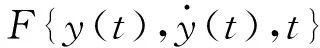
4 结 论

(1)采用正弦力激励法对金属橡胶/碟簧叠层复合结构(EMWM/DS)进行试验研究。以耗能、损耗因子和动态平均刚度等参量来表征叠层复合结构的阻尼能力。结果表明，添加金属橡胶夹芯层后，对叠层复合结构的阻尼能力有较大提升；复合结构在低频段对频率变化不敏感；随着预紧量、变形幅值以及金属橡胶夹芯层密度的增加，其耗能不断增加，而损耗因子则呈下降趋势。

(2)基于迹法等效阻尼模型，考虑弹性恢复力和阻尼力随变形幅值、频率的变化规律，用参数分解识别法建立该复合结构在一定载荷下的非对称迟滞模型。结果表明，预测的滞回曲线与实测曲线吻合，参数识别精度可以满足工程应用的要求。