实际车流荷载作用的混凝土梁桥可靠度评估

2022-10-27陈水生李锦华朱朝阳

振动与冲击 2022年20期

陈水生，赵辉，李锦华，朱朝阳

(华东交通大学土木建筑学院，南昌 330013)

随着跨区域间大宗货物运输业务的不断增加和汽车工业的飞速发展，公路运输因自身的优点而成为现代物流行业的主力军，城市道路和高速公路上的车辆越来越多且车辆规格越来越复杂。与此同时，我国桥梁建设突飞猛进，公路桥梁数量目前达到83.25万座[1]，其中中小跨径的混凝土梁桥因其结构简单、施工方便等优点，在公路桥梁中广泛应用且数量庞大。与大跨径桥梁相比，中小跨径的混凝土梁桥设计活恒载比值大，在服役期内对汽车荷载更敏感[2]，特别是车辆超重超限而导致的混凝土梁桥垮塌事故也时有发生[3]，桥梁结构在车辆荷载作用下的使用寿命和运营安全备受社会关注。为保证混凝土梁桥的结构安全，就很有必要摸清新建和在役混凝土梁桥在未来服役时间内的承载力性能变化规律。

因此，学者们对混凝土梁桥的承载力可靠度进行了大量的研究，如：Strauss等[4]研究了单片梁构件的可靠度问题；邓露等[5]分析了车辆轴限对钢筋混凝土简支梁桥可靠度和加固费用的影响；孙晓燕等[6]基于规范车辆荷载评估了钢筋锈蚀对在役钢筋混凝土简支T梁桥耐久性的影响；金浩等[7]将规范车辆荷载产生的桥梁荷载效应视为极值Ⅰ型分布，进而分析了钢筋混凝土简支梁桥加固后的承载能力变化趋势，对加固后的可靠度进行了计算；彭建新等[8]在分析氯盐环境下钢筋混凝土简支梁桥的随机失效概率时，车辆荷载效应为两辆重车并行过桥产生的荷载效应；杨慧等[9]基于规范车辆荷载考虑混凝土碳化和氯离子累积效应的影响，对混凝土梁桥后期服役阶段的承载力失效概率进行评估；吴瑾等[10]认为规范车辆荷载效应服从极值Ⅰ型分布，进而考虑钢筋锈蚀对钢筋混凝土梁桥抗弯承载力性能的影响；索清辉等[11]基于规范车辆荷载提出了计算在役钢筋混凝土梁桥时变可靠度的方法，分析可变荷载增加对桥梁承载能力的影响。

可以看出，上述研究成果较丰硕，在混凝土梁桥的设计、建造和管养中也很有参考价值，但这些研究是基于规范车道荷载，认为密集行车的车辆荷载相当于现行规范的公路-Ⅰ级，一般行车的车辆荷载相当于现行规范的公路-Ⅱ级。实际上，汽车荷载是一种社会性荷载，其与经济、政策、汽车工业之间联系紧密，实际运营汽车荷载受多种因素的影响呈现出高度的随机性，在自由通行的情况下还可能大于规范规定的车辆荷载。当然，也有学者在研究混凝土梁桥的承载力可靠度时考虑了实际车辆荷载的随机性，如：黄平明等[12]从实测车辆数据中分离出特重车荷载数据，进而研究重载交通下的空心板梁桥承载能力安全性，但其没有对桥梁在未来服役期的承载力安全性进行分析；袁伟璋等[13]采用广义pareto分布拟合车辆荷载效应的最大值分布，分析既有钢筋混凝土简支梁桥的承载力失效概率，但没有考虑桥梁抗力的退化且广义pareto分布模型的合理阈值选择很困难；罗媛等[14]考虑随机车辆荷载的冲击效应，分析钢筋混凝土梁桥的疲劳可靠度，但没有考虑桥梁抗力退化；袁阳光等[15-16]考虑桥梁抗力和车辆荷载的时变性，根据桥梁车致荷载效应的年最大值样本建立混凝土梁桥车致荷载效应极值的广义极值分布模型，但这种区间取最值的样本获取方法对桥梁车致荷载效应原始样本信息的利用率较差，浪费了很多有用的信息。鉴于此，为了克服已有研究的不足，本文根据实际运营车辆荷载数据，基于经典Rice公式的界限跨阈率理论建立随机车流荷载作用的桥梁车致荷载效应极值的概率分布模型，考虑桥梁抗力退化的时变特性，对在役混凝土梁桥在未来服役期内的承载力失效概率进行评估，为新建和在役混凝土梁桥的建造和管养提供科学的指导和事前决策依据，研究意义重大。

1 荷载效应概率分布模型

1.1 车辆荷载效应概率分布模型

1.1.1 随机车流的模拟

对于桥梁工程而言，随机车流的模拟能够更真实的再现作用于桥梁上的实际车辆荷载，为桥梁的承载力可靠度分析提供有力的支撑。任意时间的过桥车辆具有很强的随机性，其中车辆的车型、车质量、车辆间距和车辆行驶车道是考虑车辆随机性的四个主要参数。实测数据表明车辆的随机参数服从一定的概率分布，因此可以采用随机过程理论和数理统计方法来对过桥车流进行仿真模拟。本文通过对江西省高速公路管理单位在昌九高速公路的实测数据进行整理，根据下述车辆运行参数建立随机车流荷载模型。

(1)车型及车道

公路桥梁的运行车辆各异，车辆类型较多，各类型车辆具有较强的随机性，根据车辆类型现场调查结果并参考已有的研究[17]，可以将高速公路上行驶车辆分为六种代表性车型，各车型和车辆行驶车道的统计数据如表1所示，各车型出现的频率和车辆车道的选择可以采用均匀分布函数来生成[18]。

表1 车型及车道统计数据

(2)车质量

不同车辆的车质量变化较大，与地域位置及地域经济发展水平有较大关系。通常情况下，上桥车辆可以分为空载、一般载质量和重载三种情况，车质量的最小值是空载情况下车辆自身的质量，车质量的最大值与车辆的超载有关。根据实际交通监测数据，各车型的车质量统计结果呈现多峰分布的特点，可以采用高斯混合分布拟合各车型车质量[19]，拟合的高斯混合分布参数如表2所示。表2中，μi，σi分别为第i个高斯分布的均值和标准差。以C6车型为例，图1给出了其车质量的直方图和高斯混合分布的概率密度拟合结果，从图1可以看出，车质量具有明显的多峰分布特征。

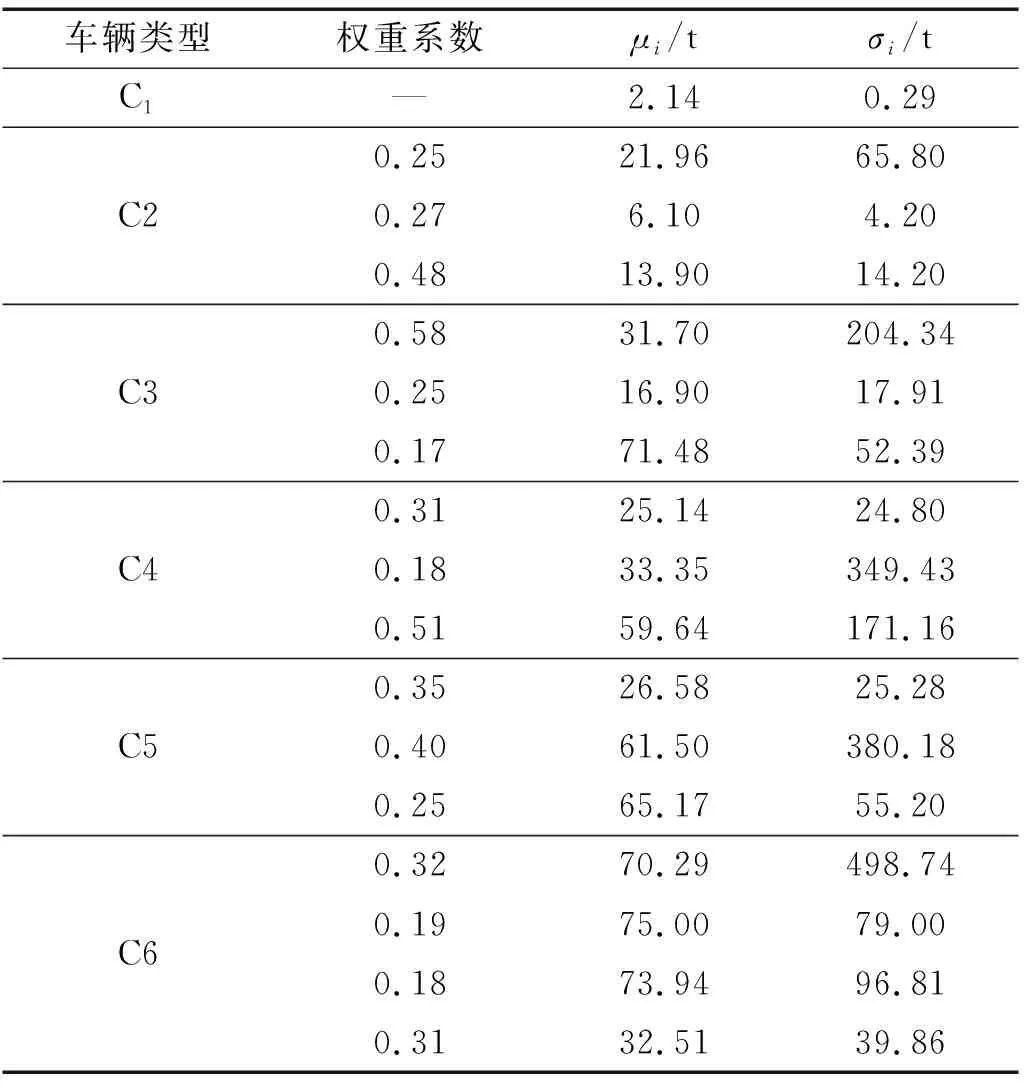
表2 车质量统计数据

(3)车距

桥上行驶车辆的间距体现了交通流的密度和车流的长度，不同的时间段，过桥车辆数量是不相同的。根据实际交通状况，可以将交通流划分为稀疏车流、一般车流和密集车流，不同车流的占比分别约为0.474，0.329，0.197，不同车流的日通行量分别约为2 988辆，2 400辆、1 020辆。稀疏和一般车流的车辆间距可以采用对数正态分布来生成车距样本，密集车流的车辆间距可以采用伽马分布生成车距样本[20]，其分布参数分别为(7.21，0.42)、(6.52，0.68)、(6.43，9.15)。根据不同车流的车辆间距样本拟合的概率密度曲线，如图2所示，从图2可以看出，随着车流密度的增大，车辆间距的均值减小，概率密度曲线的峰值越来越大，车距样本的离散性越来越小。

以一般车流为例，综合考虑车型、车道、车质量和车辆间距的随机性特征，借助MATLAB平台，采用Monte-Carlo随机抽样的方法生成某一时段的一般车流样本，如图3所示。图3中车道编号1、编号2分别为行车道和超车道。

1.1.2 经典Rice公式理论

已有的研究[21]表明，桥梁在某一车流荷载作用下的荷载效应通常可假定为平稳高斯随机过程。那么，就可以采用经典Rice公式[22]来拟合桥梁车致荷载效应与给定界限的交叉次数。设x为桥梁的车致荷载效应随机过程，单位时间内x的跨阈率v(x)可以表示为

(1)

将式(1)两边取对数，经整理可以得到

ln[v(x)]=a0+a1x+a2x2

(2)

(3)

(4)

式中，vopt，mopt，σopt分别为最优拟合的均值点跨阈率、均值和标准差。

实际上，公路桥梁过桥车流密度在不同的时间段是不同的，车流密度与人类的作息时间相关，大体呈现出白天过桥车流较密集，夜晚过桥车流较稀疏的特点。根据不同车流状态车辆荷载产生的荷载效应，采用跨阈率叠加原理对不同车流状态的车致荷载效应跨阈率模型进行叠加，可得实际车流的界限跨阈率为

vxym(x)=pxvx(x)+pyvy(x)+pmvm(x)

(5)

式中，vx(x)，vy(x)，vm(x)分别为稀疏、一般和密集车流的界限跨阈率；px，py，pm分别为不同车流的占比。

将式(5)代入式(2)，经拟合得到实际车流的最优待定参数，进而得到实际车流荷载作用的桥梁车致荷载效应极值的概率分布。

1.2 永久荷载效应概率分布模型

桥梁结构的永久荷载即是桥梁结构的自质量，永久荷载在客观上是确定的，包括桥跨的主梁质量、横隔梁质量、桥面铺装质量、人行道和栏杆质量等。虽然永久荷载在结构服役时间内的变化较小，但综合考虑各因素的影响，李扬海等[23]依然将其作为随机变量来处理，认为结构永久荷载服从正态分布，永久荷载的作用效应与永久荷载按线性比例关系处理，即永久荷载效应也服从正态分布，其概率密度函数及其分布参数如下

(6)

(7)

式中：κSG=1.014 8；δSG=0.043 1；SGk为永久荷载效应标准值；μSG，σSG分别为永久荷载效应的均值、标准差；g为永久荷载变量。

2 桥梁抗力退化概率分布模型

混凝土梁桥的抗力取决于混凝土和钢筋的强度，但由于桥梁的使用环境复杂，即使在一般大气环境，混凝土碳化、钢筋及预应力筋锈蚀、钢筋及预应力筋与混凝土黏结性能降低都会发生，因此而引起的抗力逐年退化实为一非平稳随机过程。以受压区高度在翼缘板内的T型梁为例，其正截面抗弯承载力可以表示为

(8)

式中：fsy(t)，As(t)分别为普通钢筋的强度和截面面积的时变值；fsp(t)，Ap(t)分别为预应力钢筋强度和截面面积的时变值；fcd(t)为混凝土抗压强度的时变值；b和h0分别为T型主梁的计算宽度和有效高度；ks(t)为钢筋与混凝土的协同工作系数。

从式(8)可以看出，影响抗力变化的各变量是随着时间变化的，相互之间的关系复杂，要精确确定混凝土退化强度、普通钢筋退化强度、预应力筋退化强度、钢筋与混凝土的协同工作系数是很困难的。因此，为了便于工程应用和简化计算，Li等[24]将时变抗力表示为

R(t)=g(t)R0

(9)

式中：R0为结构初始抗力，是一个随机变量；g(t)为抗力衰减函数，可以采用桥梁服役时间的二次多项式来表示[25]

g(t)=1-k1(t-T0)+k2(t-T0)2

(10)

式中：k1，k2为抗力退化速率参数；T0为抗力退化起始时间。不同退化模式的抗力退化速率参数如表3所示。

表3 抗力退化速率参数

那么，任意时刻抗力的随机性取决于初始抗力的随机性，时变抗力R(t)的均值μR(t)和标准差为σR(t)

(11)

式中，μR0，σR0分别为结构初始抗力的均值和标准差。

已有的研究表明，构件的抗力不拒绝对数正态分布，则抗力的概率密度函数为

(12)

式中，r为桥梁抗力变量。

3 实际车流荷载作用的混凝土梁桥可靠度评估方法

基于实际车流荷载，桥梁在未来服役期内的承载力性能分析主要分为四大部分：随机车流的模拟、建立车辆荷载效应极值的概率分布模型、建立桥梁抗力退化的概率分布模型、桥梁承载力性能评估，其主要计算步骤如下：

步骤1根据实测车流的车辆类型、车辆行驶车道、车辆质量、车辆行驶间距和车辆行驶状态的统计参数，采用Monte-Carlo随机抽样的方法生成满足实际交通状况的随机车流荷载模型。

步骤2将随机车流中各车辆的车轮荷载等效为集中力，考虑车辆过桥冲击力的影响，利用影响面加载的方法计算随机车流荷载产生的弯矩。基于经典Rice公式的界限跨阈率理论和跨阈率叠加原理，拟合经典Rice公式的最优参数，得到桥梁车致荷载效应极值的概率分布模型。

步骤3根据桥梁的实际运营环境，综合考虑桥梁自身抗力的退化过程，建立桥梁抗力的时变概率分布模型；并计算永久荷载产生的荷载效应。

步骤4采用JC法求解桥梁在未来不同服役期内的承载力失效概率。结构在时间点t的功能函数为

Z(t)=R(t)-SG-SQ(t)

(13)

式中：SG为永久荷载效应；SQ(t)为车辆荷载效应。

则，服役期T内的结构失效概率为

Pf(T)=P{R(t)-SG-SQ(t)<0,t∈(0,T)}

(14)

假定混凝土梁桥的破坏形态为：桥梁任意一片主梁承载力失效，就认为整个桥梁系统不再具备承载能力。因此，在计算整个桥梁体系的失效概率时，将各片主梁视为串联结构体系，整个桥梁体系的失效概率可以表示为

(15)

式中，Pfi为第i片主梁的失效概率。

综上所述，基于实际车流荷载作用的混凝土梁桥可靠度评估的流程图，如图4所示。

4 混凝土梁桥可靠度评估案例

以一座预应力混凝土简支T梁桥为工程背景，该桥位于2019年扩建后的江西省昌九高速公路永修段，桥梁跨径40 m，桥梁上部结构5片T梁组成，桥面铺装层采用4 cm厚改性沥青混凝土抗滑表层+6 cm厚中粒式改性沥青混凝土+三层FYT-1改性防水层+10 cm厚C50混凝土桥面铺装层，桥梁设计荷载为公路-Ⅰ级，设计车速100 km/h，桥梁横断面如图5所示，图5中各片梁分别编号。基于Midas/Civil软件，采用梁格法建立桥梁的有限元模型，T型主梁和横隔梁采用空间梁单元，相邻T型主梁之间采用虚拟梁单元连接，虚拟梁单元的容重为0，弹性模量与T型主梁相同，桥梁有限元模型如图6所示。

4.1 车辆荷载效应的概率分布模型

4.1.1 车辆荷载效应的求解

随机车流的车辆数量很多，如果所有车辆都采用整车模型，计算时间较长，为了简化计算，参考文献[26]的车辆轴重分配比例，将各车辆的总载质量按比例分配给每一个车轮，再将各车轮荷载简化为一个集中力。参考已有的研究[27]，为了考虑车辆过桥的冲击力影响，可以用冲击系数乘以车辆荷载来计算冲击力的大小。因此，本文在考虑过桥车辆对桥梁的冲击效应时，首先采用Midas/Civil软件计算该桥基频，其值为2.89 Hz，根据我国《公路桥涵设计通用规范》的冲击系数计算公式计算的冲击系数为0.172；然后将车轮简化集中力乘以1.172，根据随机车流荷载在桥上的作用位置，基于荷载效应影响面采用二维线性插值的方法计算过桥车辆的荷载效应。其中，影响面的计算方法为：在Midas/Civil软件里，将一个单位集中荷载(1 kN)在桥梁不同的纵断面沿着单元节点从桥梁一端移动到另一端，并计算其在所研究截面产生的荷载效应，进而组成影响面。图7给出了1 kN单位集中荷载在5片T型主梁中心线上移动时1#梁跨中弯矩的影响面。

根据实测车流的日通行量，以1#梁为例，其跨中弯矩的时程曲线如图8所示。从图8可以看出，不同车流的桥梁车致弯矩峰值随机性较强，任意一个峰值点的出现都说明有一辆重载货车过桥。

4.1.2 弯矩界限跨阈率的模拟

如果每年按250个有效日历天来计算，基于1#梁车致弯矩的时程模拟数据，用1 000天的桥梁车致弯矩样本数据来拟合经典Rice公式的最优参数。根据式(5)，图9给出了实际车流作用的弯矩界限跨阈率曲线拟合结果，从图9可以看出，经典Rice公式对桥梁车致弯矩年跨阈次数的拟合效果很好，最优拟合参数vopt，mopt，σopt分别为3 212，1 922.8 kN·m，526 kN·m。

同时，为了探究不同车流状态，即随机车流中车辆间距对本文40 m跨径简支梁桥弯矩界限跨阈率的影响，按照实测的车流占比，在此分两种情况进行讨论：情况一，稀疏、一般、密集车流具有相同的日车辆数量1 000辆；情况二，稀疏、一般、密集车流具有不同的日车辆数量，分别为实测车辆数量1 020辆、2 400辆、2 988辆。图10给出了不同车流作用的弯矩界限跨阈率曲线拟合结果，从图10可以看出：情况一不同车流作用的弯矩界限跨阈率及跨阈率曲线接近重合，桥梁车致弯矩的取值区间相同，说明随机车流中车辆间距对本文简支梁桥的车致弯矩界限跨阈率的影响很小；情况二密集车流作用的弯矩界限跨阈率最大，一般车流次之，稀疏车流最小，即车辆数量越多，则弯矩界限跨阈率就越大，说明弯矩界限跨阈率大小取决于过桥车辆数量。这与实际交通状况是吻合的，对于中小跨径简支梁桥而言，多车同时过桥的概率很小，2辆货车或多辆货车同时过桥的概率更小。据此也可以推断，桥梁跨径越小，车辆行驶间距对桥梁车致荷载效应的影响就会越小，即在研究中小跨径简支梁桥的车致荷载效应时，根据车辆间距将过桥车辆划分为稀疏、一般、密集的车流状态意义不大。

4.1.3 桥梁车致弯矩极值的概率分布

为了更切合实际情况，本文综合考虑不同车流荷载，采用跨阈率叠加原理得到的实际车流来建立车辆荷载效应极值的概率分布模型。以1#梁为例，将实际车流的最优跨阈率拟合参数代入式(4)可得其在不同服役期内的车致弯矩极值的概率密度函数

(16)

同理可得其他T型主梁的车致弯矩极值的概率密度函数，在此不再赘述。图11给出了1#梁在不同服役期内的跨中弯矩极值的概率密度演化图及其脊线，从图11可以看出：随着桥梁服役时间的增加，桥梁车致弯矩极值的均值增大，离散程度减小；在设计基准期100年内的跨中弯矩极值的均值和标准差分别为4 580 kN·m，393.3 kN·m。

4.2 桥梁抗力退化的概率分布模型

依据桥梁的设计图纸，按照一期恒载和二期恒载分别计算T型主梁跨中截面的弯矩标准值为7 148.7 kN·m，则根据式(7)可得永久荷载作用的主梁跨中弯矩的均值和标准差分别为7 254.5 kN·m，312.67 kN·m。采用我国《公路钢筋混凝土及预应力混凝土桥涵设计规范》的计算方法，本文T型主梁正截面抗弯承载力标准值为15 433.64 kN·m。考虑T型主梁抗力的逐年退化，以中等退化为例，图12给出了抗弯承载力的概率密度演化图及其脊线，从图12可以看出，随着桥梁服役时间的延长，T型主梁的抗弯承载力均值和离散程度逐渐较小。

4.3 桥梁承载力可靠度评估

该桥已服役2年，在此视为新建桥梁来分析；桥梁所处运营环境为一般大气环境，可以认为桥梁抗力的退化模式为低速退化模式。根据式(14)，图13给出了各片T型主梁在不同服役时间内的承载力可靠指标，从图13可以看出：①各片T型主梁的可靠指标随着桥梁服役期的增加而减小，直接承受车辆荷载作用的T型主梁，其承载力可靠指标小于非直接承受车辆荷载作用的T型主梁；②边梁1#梁的可靠指标最小，次边梁2#梁的可靠指标次之，因为行车道通行重载货车较多，承受较大的车辆荷载；③整个桥梁系统的可靠指标与1#梁接近，即系统的承载力失效概率取决于可靠指标最小的T型主梁；④桥梁系统在设计基准期100年内的承载力可靠指标为4.33；如果将桥梁的目标可靠指标设为β=4.7[28]，则在目前的实际交通荷载作用下，1#梁的安全储备有待提高；管养单位的监测数据表明，过桥车辆的最大载质量达到了186.7 t，为了保证桥梁的安全运营，有必要采取干预措施，将目前的自由通行变为计重收费通行或禁止超载。

当不考虑桥梁抗力的逐年退化时，图14给出了桥梁系统在不同服役期内的可靠指标，从图14可以看出：①桥梁抗力退化的可靠指标小于抗力不退化的可靠指标；在设计基准期100年内，桥梁抗力退化和不退化的承载力可靠指标分别为4.45，4.78，即桥梁承载力失效概率分别为4.31×10-6，8.84×10-7，桥梁抗力退化的承载力失效概率是抗力不退化的4.88倍；②如果将桥梁的目标可靠指标设为β=4.7，则在目前的实际交通荷载作用下，考虑桥梁抗力的低速退化，桥梁在服役到2065年时达到承载力临界状态，继续运营就需要采取维修或加固措施。

在实际车流荷载作用下，图15给出了桥梁系统在未来不同服役期内的承载力冗余度，从图15可以看出，随着桥梁服役时间的延长，桥梁抗弯承载力可靠性能冗余度逐渐下降，由初始时刻的0.41下降到第46年的0，服役到100年的可靠性能冗余度为-0.25。

为了探究桥梁抗力退化模式对桥梁承载力失效概率的影响，图16给出了桥梁系统的承载力失效概率，从图16可以看出：随着桥梁抗力退化速度的加快，桥梁在未来服役期内的承载力可靠指标迅速下降；在运营环境恶劣的情况下，混凝土梁桥应该提高抗弯承载力，特别是边梁的安全储备可以比其他主梁大。