泵站虹吸式出水流道驼峰排气过程气液两相流研究
2022-10-27刘霞黄可灿赵亮常正柏蒋劲
陈 奇,刘霞,黄可灿,赵亮,常正柏,蒋劲
(1.湖北省水利水电科学研究院,湖北武汉 430072;2.湖北省国际灌排研究培训中心,湖北武汉 430072;3.武汉大学动力与机械学院,湖北武汉 430072)
0 引言
泵站是指通过泵进行抽水、增压,再通过相关水工筑物进行输水、配水、排水的工程设施[1]。泵站在实际工程中应用较为广泛,在农业灌溉、输水调水、城市排涝等方面起着重要作用,为国家经济建设和人民的幸福生活做出了重要贡献。出水流道作为泵站的关键过流部件之一,其对泵站的效率、出水流态以及泵站的稳定运行影响较大。出水流道的形式主要有虹吸式、直管式、猫背式、屈膝式等[2]。对于虹吸式出水流道而言,其顶部装有真空破坏阀,在水泵停机时可用来破坏虹吸切断水流,运行可靠方便,且不会影响到防洪堤,工程造价较低,适用于出口水位变化不太大的泵站。
目前已经有诸多学者对虹吸式流道的相关问题进行了研究。朱红耕[3,4]采用了三维数值模拟方法分析了虹吸管内部流道的流态,发现在驼峰段和下降段水流速度变化较大时,容易发生脱流现象。谭淋露[5]采用三维数值模拟方法分析了虹吸式出水管内部水力特性,通过对比计算虹吸管不同的上升角、驼峰断面高宽比、下降角和出口断面高宽比对其水力特性的影响,确定了更优参数,降低了水力损失。模拟冯建刚[6]通过模型试验,研究了虹吸形成的3 个主要阶段,分别为水力驱气阶段、水力挟气阶段、稳定虹吸阶段。其中水力挟气阶段对形成稳定虹吸所需时间影响较大。汪尚红、李泽等[7]对虹吸式出水流道的轴流泵过渡过程进行了研究,发现开机过程出水闸门的开启时间不宜过长,以防止机组过载;关机过程出水闸门先快关后慢关,且对于不同泵站开闸和关闸相关时间都有最优值。王晓升、冯建刚等[8,9]采用RNG k-ɛ 湍流模型以及欧拉多相流模型对虹吸式出水流道虹吸形成过程进行了数值模拟计算,发现其他参数结构固定的情况下,对水力挟气阶段影响最大的是流速,流速越大所需时间越短。M.Cihan 等[10]在数值模拟时使用VOF模型,模拟出了排水过程中空气进入虹吸管的现象,在其物理模型试验中也观察到了与数值模拟类似的空气夹带现象,空气进入虹吸管时会降低排水效率并且引起振动。Babaeyan-Koopaei等[11]通过模型试验,分阶段对特定的虹吸溢流道的进气口设计和流道结构设计进行改善,在对实验模型只进行简单修改的情况下,发现在虹吸式流道特定高度的上方开一定大小和数量的水平方形槽孔,可以获得最佳的空气调节稳定性,并且提高了溢洪道的容量。Rahim等[12]采用RNG k-ɛ湍流模型和VOF模型计算出了虹吸式出水流道的流量系数,并与模型试验相对比,数据表明一致性较高,吻合较好,验证了数值模拟的可行性。
虹吸式出水流道形成稳定虹吸需要经历4 个阶段:启动阶段,水力驱气阶段、水力挟气阶段、稳定虹吸阶段[8],其中水力挟气阶段最为关键,水流需要将驼峰内的大气团带走,才能进入到稳定阶段。若将气团整体吹走,则该阶段经历的时间短,但需要的流速较大,对于大型的虹吸式出水流道,整体将气团带走所需要的流速更大;若设计流速较小,则挟气阶段的时间将增加,流速过小甚至不能进入稳定虹吸阶段。处于该阶段的时间过长,会导致驼峰处水力损失偏大,且水流状态不稳定,使泵的工况不稳定,这将引起机组产生振动、噪音等。若此时水泵工作在其特性曲线的马鞍区内,则将产生更强烈的振动和噪声,处于该工况时间过长甚至有可能造成事故。因此,研究流速大小以及出水流道的自身结构参数对虹吸形成阶段的影响,以及形成稳定虹吸所需时间,对于泵站安全高效稳定运行具有重大意义。
1 瞬态数值模拟方法
1.1 基本控制方程
流体流动遵循的三大基本定理为:能量守恒、质量守恒、动量守恒,这三大定理结合数学方法即可得到流体运动的基本控制方程。本文所研究的虹吸式出水流道中的虹吸形成过程的可压缩性不明显,可忽略能量方程,仅考虑连续性方程及动量方程。
(1)连续性方程如下:

式中:ρ为流体密度;u为流体运动速度。
(2)动量方程如下:

式中:fi为单位质量流体所受的质量力;σij为流体的应力张量。
1.2 VOF多相流模型及RNG k-ɛ湍流模型
1.2.1 VOF多相流模型
VOF 模型通过求解流域内的各相的体积分数及各相的动量方程来模拟两种及以上的流体,求解出的速度场等属性由各相共享,所有相在每个网格单元里的体积分数之和均为1。VOF 模型可应用于水中大气泡运动,含有自由液面的流动等,故可用于模拟虹吸式出水流道内的挟气过程。
在VOF 模型中通过求解各相的体积分数连续方程来追踪各相之间的界面,其方程如下所示:

式中:下标i表示模型中流体的相;ρ为密度;v为速度。
1.2.2 RNG k-ɛ湍流模型
线性涡黏湍流模型是目前在实际工程湍流问题中使用最为广泛的湍流模型,如k-ɛ、k-ω 模型等。而k-ɛ模型经过不断完善后,成为目前使用最广泛的模型,包括Standardk-ɛ、Realizablek-ɛ模型和RNGk-ɛ模型。
在之前对虹吸式出水流道的挟气过程研究中,已经比较了Standardk-ɛ、Realizablek-ɛ和RNGk-ɛ模型模拟结果与实验的相似程度,发现选用RNGk-ɛ模型的仿真结果与实验有较高的相似性[13],且RNGk-ɛ模型考虑到了湍流漩涡,对低雷诺数也适用,可信度和精度较高,故选用RNGk-ɛ模型。
RNGk-ɛ模型不可压缩流体的湍动能k方程及耗散率ε方程如下所示:
k方程:
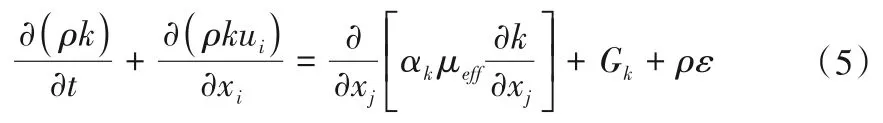
ε方程:

式中:μeff是有效湍流黏度,μeff=μ+μt;常数项取值:αk=αε=0.139,=1.42,C2ε=1.68。
1.3 几何模型及边界条件
本文涉及到的模型有3个,改变的参数为驼峰截面高宽比,分别为0.4和0.35,0.3,模型的驼峰截面尺寸均相等,面积与3 m直径的圆管相同。为了更快速地带走气泡,下降段需要保持较高的流速,故下降段没有采用扩散,快到底部时采用扩散管型以减小流速。
3 个模型总体较为相似,正视图如图1 所示,入口截面高度为H1,驼峰截面高度为H2,驼峰顶距离水面H0,出水管淹没在水面下的高度为H4,出口截面高度为H3,模型长度为L0,模型宽度为W0。模型具体尺寸如表1所示。
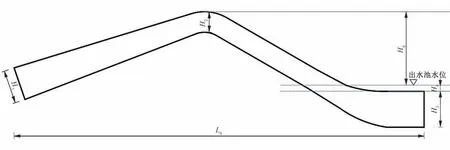
图1 虹吸式出水流道正模型正视图Fig.1 Front view of the front model of the siphon outlet channel
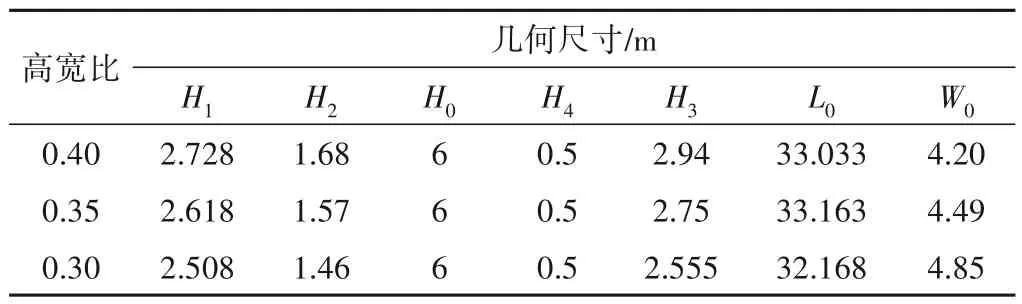
表1 模型几何尺寸数据表Tab.1 Model geometry data
3 个模型均采用速度入口和压力出口,入口流速按照工况不同则设置不同,由驼峰截面平均流速作为衡量标准,出口压力由淹没深度及出口高度共同确定,高宽比为0.4、0.35、0.3 的模型出口压力分别为19 300、18 400、17 420 Pa,重力方向设置为竖直向下。
1.4 网格划分
将高宽比为0.3,下降角为30度的模型分别按照0.03、0.04、0.05 m 的网格单元尺寸划分网格,并在相同边界条件与求解器设置下,计算至各项残差均低于10-4,设立如图2 所示的ABCD四个监测点检测流速。计算结果如表2所示。

图2 速度监测点分布图Fig.2 Distribution of velocity monitoring points
从表2中的数据可以看出,A、B、C三点流速几乎没有差别,D 点流速0.03 m 和0.04 m 单元尺寸的网格较为接近,0.05 m 单元尺寸的网格与前两者差异相对较大,故选用0.04 m 作为网格划分的主要尺寸。

表2 速度监测点结果表Tab.2 Velocity monitoring point results
采用网格单元尺寸为0.04 m 生成的网格如图3 图4 所示。图3 为高宽比0.4 模型的网格,图4 是高宽比0.3 模型仅仅缩短入口管道后的网格,缩短入口的目的在于减小网格数量,进而缩短模拟破碎带走的整个过程所需时间。高宽比为0.35 和0.3的模型网格与图3所示网格类似。

图3 高宽比为0.4的模型网格图Fig.3 Mesh diagram of the model with an aspect ratio of 0.4

图4 高宽比为0.3的模型缩短入口管段后的网格图Fig.4 Mesh diagram of the model with an aspect ratio of 0.3 after shortening the inlet pipe
1.5 求解设置
VOF 模型比较适合用来计算气团的运动,且在先前的工作中已经确定RNG k-ɛ 模型用来计算挟气过程比较适合,故选用上述两种模型来模拟气团带走的过程。使用瞬态求解,速度入口的速度大小根据不同工况设置,压力出口根据出口高度以及淹没深度共同确定,上文已经提及。管壁为无滑移边界,粗糙度为1 mm,粗糙系数为0.5,选用SIMPLE算法,计算时间步长为0.01 s,残差控制全部设置为10-4,各项残差达到10-4以下视为收敛。
2 数值模拟结果及分析
2.1 短时间内气团一次性排出计算
该部分计算了3 个不同驼峰高宽比的虹吸式出水流道,当驼峰顶部存在大气团时,一次性带走所需要的最小流速,其目的在于快速形成虹吸。气团初始状态如图5 所示,气团底部比驼峰底部略低。

图5 气团初始状态图Fig.5 Diagram of the initial state of the air masses
2.1.1 高宽比为0.4的模型一次性排出气团所需最小流速
高宽比为0.4 的虹吸式出水流道的计算结果如图6 和图7所示。设定驼峰截面流速为2.6 m/s,模拟至10 s 时的气液分布及速度云图如图6 所示。从图6(a)中可以看出,水流未能充满驼峰顶部,气泡将持续破碎并被带向出口,该流速下不能一次性排出气团。
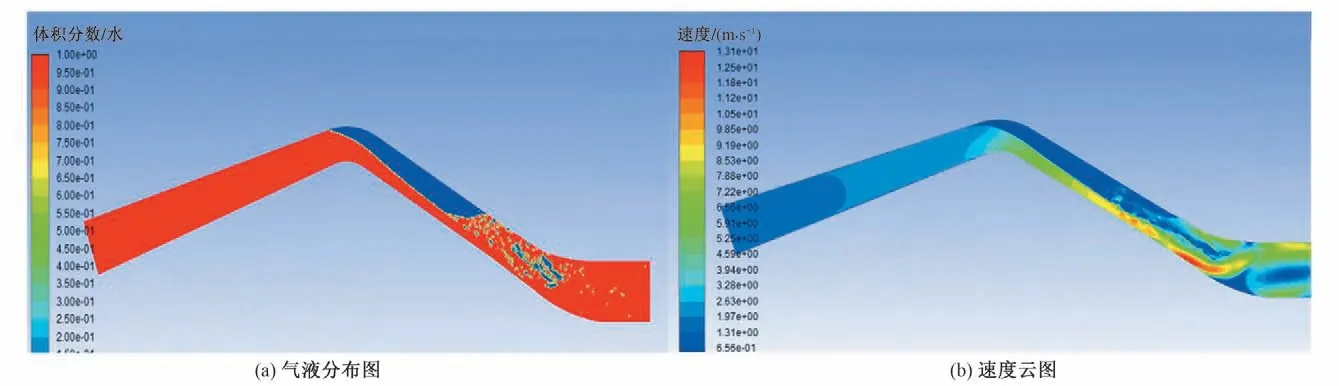
图6 驼峰截面平均流速为2.6 m/s时的结果图Fig.6 The result diagram when the average velocity of the hump section is 2.6 m/s
逐渐增大驼峰截面流速,重复计算,发现当流速增大至4.3 m/s,驼峰顶部可以直接充满水。如图7 所示,模拟至6 s时,水流可以充满驼峰顶部,后续带走气团会比较迅速,但此时驼峰截面流速为4.3 m/s,流速过大,实际工程较少采用。
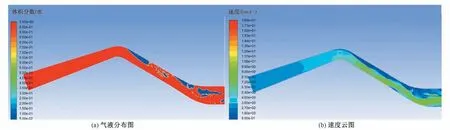
图7 驼峰截面平均流速为4.3 m/s时的结果图Fig.7 The result diagram when the average velocity of the hump section is 4.3 m/s
2.1.2 高宽比为0.35的模型一次性排出气团所需最小流速
为减小驼峰截面平均流速,将驼峰高宽比降低至0.35,计算结果如图8 和图9 所示。当驼峰截面平均流速为3.5 m/s时,模拟到6 s时发现水流未能充满驼峰顶部,如图8所示。当驼峰截面流速增大到4.1 m/s时,模拟至6 s时水流充满整个驼峰,如图9所示,后续气团排出会较为迅速。

图8 驼峰截面平均流速为3.5 m/s时的结果图Fig.8 The result graph when the average velocity of the hump section is 3.5 m/s
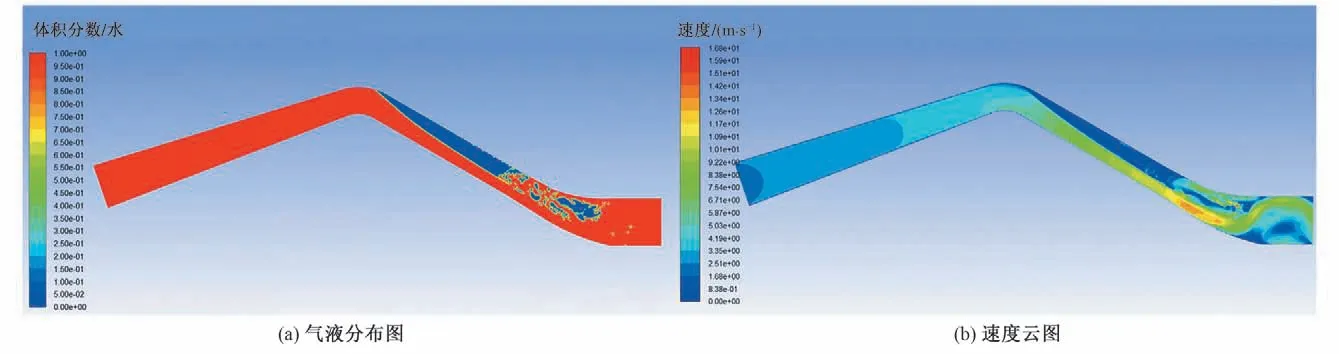
图9 驼峰截面平均流速为4.1 m/s时的结果图Fig.9 The result diagram when the average velocity of the hump section is 4.1 m/s
2.1.3 高宽比为0.3的模型一次性排出气团所需最小流速
为了进一步减小驼峰截面平均流速,减小驼峰高宽比至0.3,计算结果如图10 和图11 所示。图10 是驼峰截面流速为3.5 m/s,模拟至6 s时的气液分布及速度云图,从图10(a)中可以看出,水流未能充满驼峰顶部,需增大流速。

图10 驼峰截面平均流速为3.5 m/s时的结果图Fig.10 Result diagram when the average velocity of the hump section is 3.5 m/s
当截面流速增大至3.8 m/s时,模拟至6 s 时水流可以充满驼峰顶部,如图11(a)所示。
综上,高宽比为0.4、0.35、0.3 的模型一次性排出的流速分别为4.3、4.1、3.8 m/s,降低高宽比后,一次性排出气团所需要的临界流速有所减小,但此流速仍显偏大,所以大口径的虹吸式出水流道想要短时间一次性整体将气团从驼峰顶部排出需要较大的流速。
2.2 气团破碎带走计算
从上述结果来看,驼峰截面高宽比越小,一次性排出气团所需流速越小,故选用高宽比为0.3 的模型来进行气泡破碎带走全过程模拟,有利于进一步降低流速。本节模拟出了120 s和180 s 排气时间内将气团全部排出所对应的驼峰平均流速以及排气全过程。
2.2.1 排气时间为120 s的气团排出过程
当排气时间为120 s时,气团破碎排出过程及形成稳定虹吸时的速度云图分别如图12 和图13 所示。图12 所示的(a)~(f)的6 个状态分别为0.3、8、34、50、80、120 s 时的气液分布状态,图12(f)所示的状态为最终的虹吸形成状态,气泡完全排出,整个过程耗时120 s,此时驼峰截面平均流速为3.0 m/s。从图13 的速度云图可以看出,形成稳定虹吸后,驼峰截面在竖直方向有较大的速度梯度。

图12 驼峰截面平均流速为3.0 m/s时的排气过程Fig.12 The exhaust process when the average velocity of the hump section is 3.0 m/s

图13 驼峰截面平均流速为3.0 m/s时形成虹吸后的速度云图Fig.13 Velocity diagram after siphon formation when the average flow velocity of the hump section is 3.0 m/s
2.2.2 排气时间为180 s的气团排出过程
当排气时间为180 s时,气团破碎排气过程及形成稳定虹吸时的速度云图分别如图14 和图15 所示。图14 所示的(a)~(g)的6个状态分别为0.3、8、34、50、80、120、180 s时的气液分布状态,图14(g)所示的状态为最终的虹吸形成状态,气泡几乎完全排出,整个过程耗时180 s,此时驼峰截面平均流速为2.5 m/s。相较于120 s 的排气时间,驼峰截面流速从3.0 m/s 降低到了2.5 m/s,降低了16.67%。从图14(e)和图14(f)可以看出,排出驼峰顶部的少量气体所耗的时间较长,即驼峰顶部的气体相较于下降段内的气体更难排出,结合速度云图可以看出,由于存在垂直方向上的速度梯度,驼峰顶部流速较小,这是驼峰顶部气体更难排出的主要原因。

图14 驼峰截面平均流速为2.5 m/s时的排气过程Fig.14 The exhaust process when the average velocity of the hump section is 2.5 m/s

图15 驼峰截面平均流速为2.5 m/s时形成虹吸后的速度云图Fig.15 Velocity diagram after siphon formation when the average flow velocity of the hump section is 2.5 m/s
2.3 排气过程不同时间点湍流动能分布
对驼峰截面流速为2.5 m/s 的排气过程中t=10 s 和t=80 s 时刻进行湍流动能进行分析,其分布分别如图16、17所示。

图16 t=10 s时的气液分布及湍流动能分布Fig.16 Gas-liquid distribution and turbulent kinetic energy distribution at t=10 s
从上面的结果可以看出,t=10 s时,下降段中气液交界面附近的湍流动能较大,气团破碎迅速;而当t=80 s时,驼峰段中气液交界面附近的湍流动能大大减小,气团破碎速度变慢。这说明湍流动能的大小会影响气团的破碎速度。
3 结论

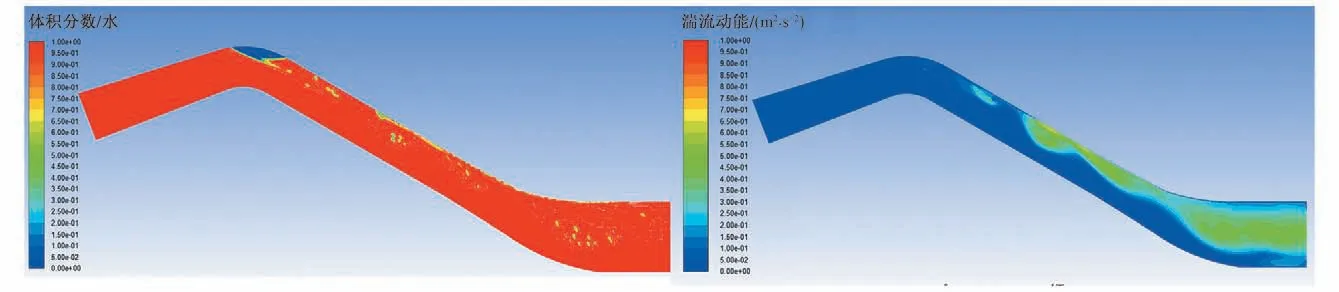
图17 t=80 s时的气液分布及湍流动能Fig.17 Gas-liquid distribution and turbulent kinetic energy distribution at t=80 s
基于CFD 研究了以两种方式带走大口径矩形断面驼峰顶部大气团,分别是一次性快速排出气团和一定时间内破碎排出气团,其中前一种方式计算了0.4、0.35、0.3 三种不同高宽比的虹吸管模型,而后一种方式采用0.3 高宽比的模型模拟了两种不同流速下气团运动、破碎带走、形成虹吸的整个过程,结论如下。
(1)降低高宽比可以降低一次性排出气团需要流速va。模型驼峰高宽比为0.4、0.35、0.3时,对应的va分别为4.3、4.1、3.8 m/s,0.3 高宽比的模型与0.4 高宽比的模型相比,va降低了11.6%。虽然有所降低,但流速仍然偏大,所以较大口径的虹吸式出水流道不建议采用一次性排出气团的方式。
(2)允许排气时间越长,对应的驼峰截面流速越小,驼峰顶部的气体相比于下降段中的更难排出。当排气时间tb为120 s时,对应的驼峰截面流速vb为3.0 m/s,当tb为180 s时,对应vb为2.5 m/s,流速降低了16.67%。由于驼峰顶部存在垂直方向上的速度梯度,顶部流速较小,且排气过程中驼峰段的湍流动能较小,使得驼峰顶部气体比下降段中的气体更难排出。
