输水管线启动填充过程含滞留气团瞬变流数值模拟

周 领，刘 静，黄 坤，刘德有

(河海大学水利水电学院，江苏 南京 210098)

输水管道作为水电站、火电站、城市供/排水、长距离供水、跨流域调水等重大工程中的重要组成部分[1-5]，一旦发生事故，不但会影响整个工程的正常稳定运行，而且可能造成极其严重的社会经济损失，甚至导致人员伤亡[1, 6-11]。输水系统所出现的破坏事故，很多与含滞留气团瞬变流有关[12]。然而，目前管道系统的设计标准并不考虑滞留气团的存在及其危害，尚无相应的计算标准，且对水气耦合作用机理和变化规律缺乏准确的认识[13-15]。

在输水管道系统的启动填充过程中，常会发生水流冲击滞留气团的复杂瞬变流，极易引起异常压力波动，影响系统安全运行甚至导致爆管事故，该现象引起了很多学者的广泛关注。Martin[1]首次建立了水流冲击滞留气团现象的刚性水体数学模型，但其模型忽略水气交界面的运动。Izquierdo[3]对Martin[1]的刚性数学模型进行改进，考虑了水气交界面位置动态变化，建立了充水排气的刚性数学模型，并指出水体间滞留气团的快速压缩会引起异常压力增大。Liou等[7]针对起伏管道系统初始上游阀完全放空的充水过程，建立了相应的刚性数学模型，但未考虑滞留气团的影响。刘德有等[12]建立了起伏变特性管道系统中水流冲击单个气团的刚性数学模型。虽然刚性数学模型具有简单、快捷的优点，但其应用具有一定的局限性，如滞留气团含量较小时，可能会得到错误结论。Zhou等[13, 16-21]研究了水流冲击滞留气团的瞬变压力及参数变化规律，发现水气耦合作用机理复杂，且可能引起10倍于入口压力的危险峰值压力。

综上所述，水流冲击滞留气团可能会引起异常压力波动。已有研究成果大部分集中于简单管路中含单个滞留气团的情况，对于起伏管道内水流冲击多段气团的瞬变流，相关成果少，水气作用规律尚不完全清楚。本文针对管道启动填充过程中含1段或2段滞留气团瞬变现象，考虑了水体弹性、气体可压缩性、水-气交界面的运动及多段气团间的相互作用，建立了相应的数学模型。通过与试验结果对比，验证了所建模型能有效地预测快速充水过程中含1段或2段滞留气团的压力变化，并进行算例分析研究。

1 试验装置

试验观测研究是在河海大学水电站实验室“管道系统中水气两相耦合瞬变流”试验平台进行。如图1所示，整个系统从上游至下游依次由蓄水池、不锈钢多级潜水泵、螺纹式球阀、气罐(压力罐)、电磁流量计、球阀、进气孔口、排水阀、完全敞开的末端组成。水泵与气罐之间通过不锈钢钢管连接，压力罐至下游由一段1 m长的不锈钢和多段起伏的有机玻璃透明管道组成。从气罐出口至管道末端为水流冲击滞留气团的试验研究管道，总长为10.97 m，有机玻璃管道内径4 cm，壁厚1 cm。

图1 含滞留气团管道系统启动填充的试验装置

试验中，将气罐出口和管道入口交界面定为x=0，水平管道中心线定为z=0。图1中给出了管道弯曲段最高点和最低点处的沿线长度x和高程位置z；P1,P2,…,P7为直管段编号；球阀距上游入口距离为2.236 m；共有8个压力传感器(pressure transducer, PT)，其安装位置分别如下：PT1(x=10.82 m,z=0.632 m)，PT2(x=9.15 m,z=0.075 m)，PT3(x=7.60 m,z=0.82 m)，PT4(x=6.68 m,z=0.24 m)，PT5(x=5.75 m,z=0.32 m)，PT6(x=4.33 m,z=0.96 m)，PT7(x=1.707 m,z=0 m)，PT8(x=1.337 m,z=0 m)。在弯曲管道最顶部和最底部分别安装3个进气孔、4个排水阀，安装位置见图1，仅用于调节初始状态下的气团段数和长度，在瞬变过程中均处于关闭状态。各压力传感器性能一致，测量范围为0～0.5 MPa。电磁流量计性能参数：公称通径为DN40，流量范围为0～25 m3/h。数据采集系统为美国国家仪(产品型号为PCI-6221，采样率为250 kS/s)。

本试验研究主要用于所建数学模型的验证。分别针对含1段、2段初始滞留气团情况，进行了4种工况试验，入口压力水头Hr均为8.15 m，初始冲击水体长度xf0均为 3.3 m。各工况下，阻断水体1上、下游位置xbu,1、xbd,1，阻断水体2上、下游位置xbu,2、xbd,2，及对应气团1和气团2初始长度La0,1、La0,2，阻断水体1和阻断水体2初始长度Lb0,1、Lb0,2，具体初始状态值见表1。为了便于计算分析，基于恒定流状态，试验测得管道入口至阀门的上游段电磁流量计、全开状态下的球阀、法兰等局部损失系数约为2.4～2.7；起伏管道部分平均阻力系数变化范围为0.016～0.024。高速摄像机的拍摄记录显示，试验中手动球阀的开启时间(从全关至全开)为0.07～0.09 s，实测水锤波速约为400 m/s。

表1 4种试验工况相关参数初始状态值 单位：m

2 数学模型

2.1 瞬变过程描述

结合试验观察结果，含多段滞留气团的输水管线启动填充过程可描述如下：初始时，上游阀门完全关闭，阀门上游段为高压段，与压力罐相连，阀门下游段管道系统中滞留n段气团和阻断水体(图1中n=2)；当上游阀门瞬间打开之后，管道系统开始充水排气，靠近上游的第1段滞留气团在冲击水体的作用下开始压缩，其压力逐渐增大，到一定值时，开始推动第1段阻断水体向下游运动。与此类似，其他部分滞留气团也受到压缩，压力增大推动阻断水体运动。管道系统末端完全敞开，在冲击水体的推动下，第n段阻断水体开始流出管道系统；当第n段阻断水体完全流出时，第n段气团开始排出管道系统；以同样的方式，最终管道内所有滞留气团将排出管道系统。

2.2 基本假定

针对起伏管道快速启动填充过程中含有多段滞留气团的瞬变流，数值模拟的基本假定包括：①管道内滞留气团为理想气体，满足气体热力学多变过程方程；②在稳态和瞬态情况下，管道内的水流阻力特性不变；③水气交界面始终与管道中心线垂直。

2.3 控制方程

在气团完全排出管道之前的任意时刻，模型包含冲击水体、阻断水体、滞留气团及水气交界面四大部分。

a.水体控制方程。考虑水体的可压缩性，其连续方程和动量方程为

(1)

(2)

式中：H为测压管水头，m；a为波速，m/s；g为重力加速度，m/s2；Q为水体流量，m3/s；f为管道摩阻；D为管道的直径，m；A为管道截面积，m2。

b.气团控制方程。封闭气团遵循理想气体状态方程，第i个滞留气团的控制方程如下：

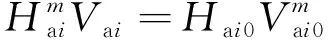
(3)

式中：Hai、Vai、Lai分别为阀门开启后t时刻第i个气团的瞬态绝对压力、体积和长度；Hai0、Vai0、Lai0分别为Hai、Vai、Lai在初始状态的值；m为理想气体多变指数。末端气团与外界相通，其气体为大气压力。

c.阻断水体两端水气交界面控制方程。描述气水交界面瞬变状态的控制方程即交界面两侧的连续方程和压力平衡方程为

(4)

Haw=Ha+Z(xaw)

(5)

式中：xaw,vaw,Haw,Z(xaw),Ha分别为水气交界面的位置、运动速度、绝对压力、位置高程及其相邻气团的压力。对于给定的管道系统，Z(xaw)是已知的；xaw0为xaw的初值。

数学模型由水体的连续和动量方程、上游入口控制方程、滞留气团控制方程及水气交界面控制方程组成，模型充分考虑了水体长度变化及所有水体的弹性。

2.4 模型求解

边界条件和初始条件：①管道填充过程中，下游出口始终为大气压力；②瞬变过程中，上游水库水位基本保持不变；③初始时，滞留气团压力为大气压力，初始流速为零；④水气交界面的压力和位置随时间是不断变化的，但任一瞬变时刻其值径向不变。

a.水体内部计算节点。对于水体内部固定网格长度的计算节点，方程如下:

C+:HP=HA+BQA-(B+R|QA|)QP

(6)

C-:HP=HB-BQB+(B+R|QB|)QP

(7)

式中：Δx为特征线网格管段长度；Δt为计算时间步长。

联立式(6)和式(7)可得水体内部计算网格节点上的Q和H：

(8)

(9)

其中CP=HA+BQACM=HB-BQB

RP=B+R|QA|RM=B+R|QB|

式中：CP、CM、RP、RM均为特征线求解过程中间变量。

b.上游进口边界。在整个瞬变过程中，上游水库水位保持不变，当考虑进口的局部水头损失时，管道上游进口边界条件为

(10)

式中：Hu为上游水库进口处压力；ξj为入口局部损失系数。水体正向流动时，ξj=0.5；负向流动时，ξj=1。联立式(7)和式(10)，采用牛顿迭代法即可求得上游边界的Q和H。

c.阀门处。将阀门出流方程与特征线方程联立，即可求解阀门处的Q和H。

d.水气交界面。水气交界面因两侧压差的存在，导致其位置是动态变化的，在考虑水体弹性的情况下，这样的动边界问题给常规的定网格的特征线法计算带来了困难。图2为该模型的计算求解网格，图中C、D点分别表示t、t+Δt时刻水气交界面的位置(t时刻各节点物理量均已知，t+Δt时刻各节点物理量均待求)。在整个计算过程中，水体网格的计算步长Δx是保持不变的，但对于邻近水气交界面的一小段水体ΔL(水气交界面至邻近水体计算节点的距离)，因随水气交界面而变化，可能不等于Δx，可见求解ΔL段水体两端节点是关键。

图2 固定时间间隔的x-t网格

下面以冲击水体下游侧水气交界面计算为例进行分析。首先，P点各参数值求取方法如下：

C+特征线，从A点至P点为

HP=CP-RPQP

(11)

C-特征线，从C点至P点为

联立式(6)(7)即可得HP和QP。

其次,D点值各参数的求取方法如下：由于D点是追踪水气交界面的动态点，无法用定网格的特征线法求解，此处需构造一辅助计算节点G(图2)，并结合气体控制方程进行求解。

C+特征线，从G点至D点为

(13)

水气交界面，从C点至D点为

(14)

由水气交界面处的压力平衡方程可得

HD=Haw=Ha+Z(xaw)

(15)

联合式(3)和式(15)可得

(16)

G点位置与P点相同,但发生时刻不同。如图2所示，HG、QG由已知点线性插值求得，根据D点位置的不同，G点取值不同：当 0<ΔL≤Δx时，HG、QG由点P和点E参数值线性插值求得；当 Δx<ΔL≤2Δx时，HG、QG由点E和点F参数值线性插值求得。第1段阻断水体的上游侧水气交界面的压力H1、流量Q1、位置x1的求解方法与上述冲击水体下游侧水气交界面计算类似。7个未知数(HD,QD,xD,Ha,H1,Q1,x1)可通过联立方程采用四阶龙哥库塔法求得。

最后考虑计算节点的删除和增加。为了便于求解，取0.5Δx≤ΔL<1.5Δx，气团压缩和膨胀，可能导致1.5Δx≤ΔL或ΔL<0.5Δx的情况，这时要对水体计算节点进行删除或增加处理，即保证0.5Δx≤ΔL<1.5Δx。对于新增计算节点可以由相邻节点的参数值线性插值求得。

图2中，第i段阻断水体的水气交界面计算节点Pui、Pdi(分别为上、下游侧)与上述冲击水体下游侧水气交界面节点计算类似。

3 模型验证

为了验证模型的正确性，将计算结果和试验结果进行比较。计算中，所需管道系统参数已在前文试验中进行了测量，但很难测定多变指数m的值。为了便于数值计算，一般令气团压缩和膨胀变化过程中多变指数保持不变。试验中，阀门快速开启，瞬变过程持续时间均在数秒之内，将滞留气团的压缩膨胀视为等熵变化[22]，取m=1.4。数值计算和试验对比结果验证了m=1.4的合理性。此外，试验观测到，阀门快速开启之后，充水排气过程中气团具有较好的完整性，即使在管道拐弯点，也未出现气团分裂现象。这说明模型中“水气交界面与管中心线垂直”的假定在系统快速启动下是合理的。

图3为系统含1段滞留气团情况下的数学模型计算与试验观测的压力变化曲线对比；图4为系统含2段滞留气团情况下的压力变化曲线对比。通过对比可知，模型计算结果与试验结果吻合度较高，对于该试验下的管道内压力变化、最大压力峰值及波动周期，本文所建立的数学模型均能进行有效的预测。本文模型亦具有一定的局限性：当充水过程极为缓慢时，尤其在管道高处拐点及其下游管段位置，可能会出现水气分层现象， “水气交界面与管中心线垂直”假定将可能引起一定的计算误差。因此，针对末端敞开的输水管道系统的快速充水排气过程，本文所建数学模型能够有效地预测其压力波动。

图3 含1段滞留气团时模型计算和试验结果比较

图4 含2段滞留气团时模型计算和试验结果比较

4 算例分析

下面以1段和2段气团为例，分析系统启动填充过程中系统最大压力的变化规律。为了方便分析参数对压力变化的影响，假定管道是水平的。管道系统基本参数如下：3种入口压力(Hr=10 m,30 m,50 m)，出口压力始终为大气压力，管道总长L=100 m，管道内径D=0.04 m，水锤波速a=400 m/s，3种管道摩阻(f=0.001,0.005,0.015)，冲击水体的初始长度Lf0=5 m。同时，假定在整个瞬变过程中m=1.4。

对于含1段气团的情况，主要研究不同管道摩阻(f=0.001,0.015)下，滞留气团和阻断水体长度变化对压力的影响。对于含2段气团的情况，主要研究不同气团2长度(La0,2=1 m,5 m)和阻断水体2长度(Lb0,2=10 m,50 m)下，上游阻断水体1长度变化对压力的影响。

4.1 含1段滞留气团情况

当仅含1段滞留气团时，气团最大压力发生在第一峰值，其后压力峰值逐渐衰减，如图3所示。气团最大压力主要取决于滞留气团和阻断水体的长度。如图5(a)所示，随着气团长度增大，气团最大压力先增大后减小，其最大值基本发生在初始气团长度较小的情况。如图5(b)所示，随着阻断水体长度增大，气团最大压力逐渐增大，尤其当阻断水体长度较短时，趋势较明显。此外，较小的管道摩阻将导致较高的压力峰值。

图5 含1段滞留气团时系统最大压力与相关参数的关系

4.2 含2段滞留气团情况

对于含2段滞留气团的情况，由于气团间阻断水体的前后运动，压力波动变得复杂。上游气团1的压力主要取决于阻断水体1的惯性、运动方向及冲量。

a.当阻断水体1较短时，阻断水体惯性很小，甚至达到可以忽略的程度，其两端气团的压缩、膨胀基本同步，最大压力值出现在第一峰值，其规律与单气团情况一致，如图6(a)所示。此时，随着阻断水体1长度增大，气团1最大压力将增大(图7)。

图6 含2段滞留气团时系统气团压力变化与阻断水体长度关系(Hr=50 m,La0,2=5 m,Lb0,2=10 m, f=0.005)

图7 含2段滞留气团时阻断水体对气团最大压力的影响(Hr=50 m,La0,1=5 m, f=0.005)

b.当阻断水体1很长时，其惯性决定了气团1的压力，其后气团2的影响可以忽略，其规律也与单气团情况一致，如图6(d)所示。此时，随着阻断水体1长度增大，气团1最大压力缓慢增大(图7)。

c.当阻断水体1处于中间尺寸时，在气团1第二次压缩过程中，阻断水体1可能向上游运动，与冲击水体同时压缩气团1，而引起较高的压力峰值，其值可能高于第一峰值压力，如图6(b)和图6(c)所示。此阶段中，随着气团间阻断水体长度增大，气团1最大压力先来自于第一峰值，后来自于第二峰值，再来自于第一峰值。因此，如图7所示，当阻断水体1长度增大时，上游气团1的最大压力呈先快速增大后减小再缓慢增大的趋势。

对于下游气团2来说，阻断水体1等同于冲击水体。由于阻断水体1上、下游的运动，气团2的压力变化曲线特点与气团1一致。但是，气团2最大压力变化规律与气团1不同之处在于：如图7所示，当阻断水体1很长时，随着阻断水体长度增大，气团2的最大压力逐渐减小。

对于含2段滞留气团的情况，较长阻断水体1、较小气团1将会引起气团1产生较高的压力；较长阻断水体2、较小气团2将促进气团2峰值压力的增大。因此，如图7所示，随着阻断水体1长度增大，系统最大压力交替来自于上游气团1和下游气团2。

5 结 语

本文充分考虑了水体弹性、气体可压缩性、水-气交界面的动态运动以及多气团间相互作用，推导建立了含多段滞留气团的输水管线快速启动填充过程的数学模型。同时，提出了局部插值法用于动态追踪水气交界面，实现了传统特征线法对于该类问题的求解。计算结果与试验结果对比验证了该模型能够准确地模拟输水管道系统含1段或2段滞留气团的快速启动填充过程中水气耦合的瞬变压力。对于仅含1段滞留气团的情况，气团最大压力发生在第一峰值，其后压力峰值逐渐衰减。随着气团长度增大，气团最大压力先增大后减小，其最大值基本发生在初始气团长度较小的情况；随着阻断水体长度增大，气团最大压力逐渐增大。对于含2段滞留气团的情况，由于气团间阻断水体的前后运动，气团最大压力可能出现在第二峰值。但对于很短或很长的气团间阻断水体，气团最大压力仍出现在第一峰值。较长阻断水体将有利于其上游滞留气团产生较高的压力峰值。对于含2段滞留气团的情况，系统最大压力可能来自于上游滞留气团，也可能来自于下游滞留气团。