坡度变化对竖缝式鱼道水力特性的影响研究
2022-10-27陈柏宇袁浩何小泷
陈柏宇,袁浩,何小泷
(1.重庆交通大学河海学院,重庆 400074;2.重庆交通大学西南水运工程科学研究所,重庆 400016)
0 引言
大坝等拦河工程的修建在发挥航运、发电、取水等巨大综合效益的同时,也会对生态环境造成一定的负面影响,如造成鱼类自然通道阻断[1],通常通过构建鱼道、升鱼机等人工通道予以缓解。竖缝式鱼道作为广泛使用的鱼道形式之一,适合习惯生活在表、中、底层的鱼类进行洄游,且能够在有限的距离内减小上下游水头差对鱼类上溯带来的影响。相关研究表明,竖缝式鱼道的隔板形式、池室长宽比、坡度等因素均会对鱼道池室内水流结构产生影响,进而影响过鱼效率[2]。
针对竖缝式鱼道,目前已开展了诸多实验研究和相应的数值模拟研究。Rajaratnam 等[3]系统研究了不同隔板形式对竖缝式鱼道的水力特性的影响,同时还发现无量纲流量与常规池室中心位置的相对水深呈正比关系,并据此提出了无量纲流量公式;Wu 等[4]通过对不同坡度的鱼道开展系列模型实验,发现当底坡为5%时,水流流速呈现二维分布,即相对于平面流速,垂向流速变化可以忽略不计,但当坡度增加,池室内开始呈现三维特性;Barton 与Keller[5]对竖缝式鱼道开展了三维数值模拟研究,将模拟结果中的水流流速分量和水深变化与相应物理模型试验数据进行量化对比,证明基于VOF 方法的RNGk-ε湍流模型可以准确获得竖缝式鱼道内的流场信息。Liu 等[6]发现在鱼道坡度为10%时,鱼道流场发生变化,射流直接冲击壁面,导致池室流态不适合鱼类洄游。An 等[7]对比了4.2%坡度下“L”型隔板与2.6%坡度下光滑型隔板竖缝式鱼道的水流流场,发现“L”型形成的“Ω”流态能够降低主流流速,减少鱼类能量消耗,有助于延长鱼类的上溯距离。Li等[8]开展了两种隔板形式下不同坡度的鱼道内流场分布的研究,其研究结论指出只要相邻池室水位差相等时,即使坡度完全不同,竖缝处的流速也几乎相等,并引入了涡量作为鱼道水力指标,通过涡量初步开展了鱼道适宜性评价。李苏等[9]发现适当增大竖缝宽度与池室宽度之比b/B可有效降低竖缝平均流速,此外,移除导板能减小末端竖缝的平均流速,但池室内主流会过于集中,不利于池室内动能耗散。
坡度作为鱼道设计的重要参数之一,直接影响鱼道内水力特性,同时还关系到建造成本和工程投资。面对拦河建筑物上下游水头差,通过增大坡度能够减少池室数量。不过,因此带来的池室内水力结构改变,尤其是主流流速等直接增大,可能降低过鱼效率,甚至导致鱼类无法洄游。目前,针对竖缝式鱼道坡度的研究主要集中在大跨度对比(5%、10%、15%、20%),同时,由于坡度增大产生的垂向流速变化会影响鱼类洄游,学者们更加关注5%以下流速呈二维分布的竖缝式鱼道。但是,仍不乏一些具有较高爆发泳速的鱼类,如鲑鱼[10]、鲟鱼[11]等,有能力通过较大坡度的鱼道。已有研究表明坡度大于10%会导致池室内产生不适合鱼类洄游的流态,因此研究中选取鱼道坡度均小于10%。
利用数值模拟系统分析不同坡度对池室内水力特性的影响,选取了两种小于5%的典型坡度1.50%、4.20%以及两种较大坡度6.67%、8.33%。重点分析了坡度变化对池室的流速分布和紊动能分布的影响。
1 数学模型
1.1 模型选择
针对鱼道池室内的复杂紊流,采用RNGk-ε湍流模型,该模型通过修正紊动黏度,在ε方程中考虑了时均应变率,能够较好地模拟流线弯曲程度较大或高应变率流动。控制方程如下:
连续方程:

动量方程:
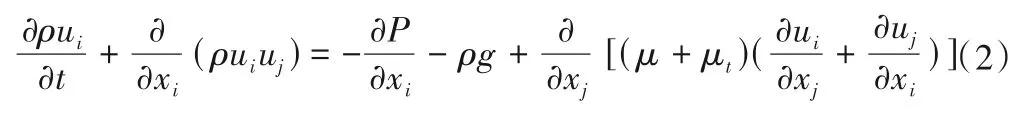
紊动能k方程:

耗散率ε方程:
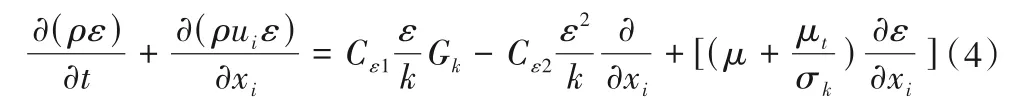
式中:u为x方向的速度分量;μ、μt为黏性系数和紊动涡黏系数;ρ为密度;P为时均压强;Gk为紊动能产生项,Gk=。方程中模型常数取值分别为Cμ=0.084 5,Cε1=1.42,Cε2=1.68。
多相流自由表面捕捉采用流体体积法(VOF)。VOF 法通过在流体域构造流体体积函数来追踪空间网格内的流体体积变化,并据此构造自由面形状。当第q相流体的容积分数αq=0时,表示控制体内无q相流体;αq=1 时控制体内充满q相流体;0<αq<1 控制体内充满部分q相流体;对所有流体相的容积分数总和为1。αw的控制微分方程为:

式中:t为时间;ui和xi分别为速度分量和坐标分量(i=1,2,3)。通过求解该连续方程来对水气界面进行跟踪。
1.2 计算区域与网格划分
计算区域包括鱼道进口、鱼道出口以及七个池室。每个池室长3.1 m,宽2.2 m,竖缝宽度0.35 m。选用了4种鱼道坡度,分别为1.50%、4.20%、6.67%、8.33%。数值模拟中鱼道进出口分别采用压力进口和压力出口,顶部设置为压力进口,参考压力为标准大气压。上下游运行水深设为恒定水深1.5 m。鱼道边壁设置为无滑移壁面。模型网格采用收敛性较好的六面体网格对计算区域进行划分,4 种坡度条件下鱼道设计的网格数量均为20 万左右,同时对竖缝区域进行了局部加密,以更好地反映竖缝流速变化,如图1所示。
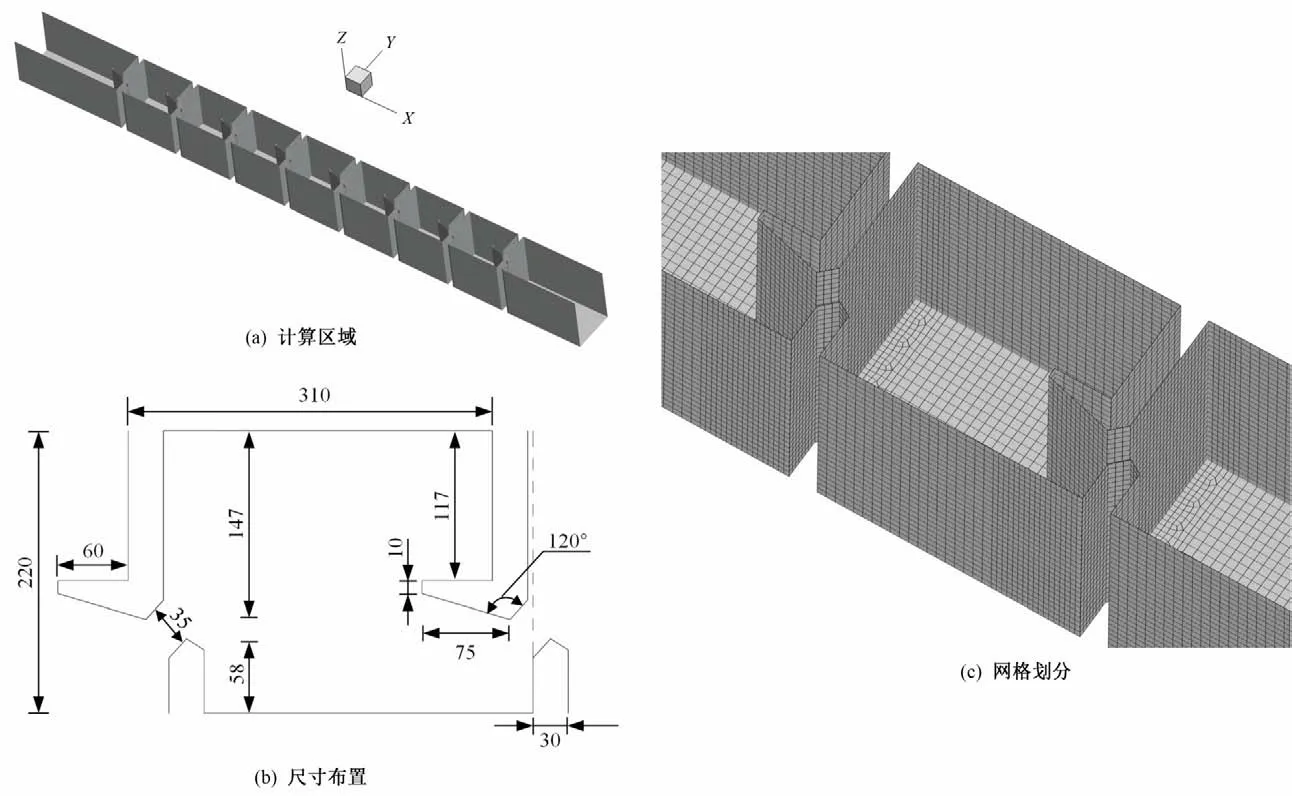
图1 计算域与网格划分(单位:cm)Fig.1 Computational domain and mesh description
2 模型验证
数值验证所选用实验数据通过坡度为1.5%的鱼道局部模型获得,该模型包含12 个常规池和1 个休息池,模型比尺为1∶5,拟利用休息池上游的7个池室的流场特性对数学模型进行验证,并开展相应的网格密度分析。该模型包括一个长度为10.26 m 的混凝土水槽和水循环供应系统,如图2所示。用于验证的流速采用三维多普勒流速仪ADV进行测量,鱼道模型池室测点分布如图3 所示。上游水位由水库中的平水槽控制,下游水位采用溢流板进行控制。为减少上下游边界条件引起的影响,选取第4池室作为典型池室开展验证。

图2 鱼道平面布置图Fig.2 Diagram of fishway model

图3 测点控制(单位:cm)Fig.3 Layout of measuring points
对数学模型进行网格独立性验证,选择3 种尺度网格进行试算,平均网格大小、节点数及网格数量如表1所示。典型池Ⅳ号断面测量流速与数值模拟结果对比如图4 所示。相对于M2和M3,M1 由于网格数量少,导致计算精度偏低,与实测数据偏差较大。而M2 与M3 的模拟结果相差不大且更接近实测数据,因此可以认为网格数量满足网格独立性要求,同时,考虑计算效率,采用平均网格大小为9 cm的M2作为网格密度。
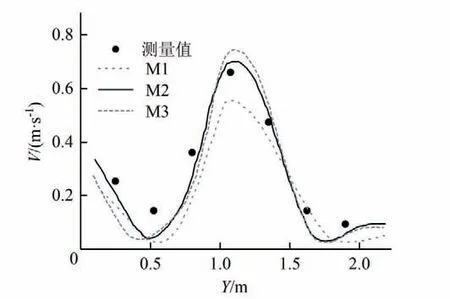
图4 不同网格尺度下断面Ⅳ流速分布与试验对比Fig.4 comparison of experimental velocity distribution in section IV and numerical results with different grid size

表1 网格独立性验证Tab.1 Verification of independence of grid size
典型池中各测点的流速模拟值与模型测量值对比如图5所示,误差范围取±0.1 m/s[7]。池室内3 个平面共156 个测量点超过70%的数据在误差范围内,且典型池前后竖缝计算值与测点最大误差仅4.1%(表2),因此可以认为模拟结果可靠性满足后续研究要求。
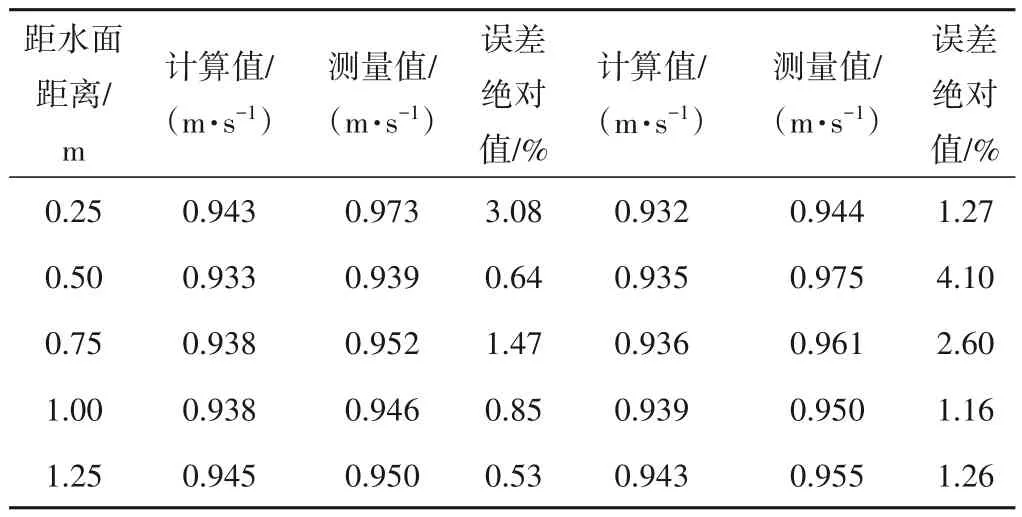
表2 竖缝流速计算值与测量值比较Tab.2 Comparison between numerical and experimental value of vertical slot velocity

图5 池室内模拟值与测量值比较Fig.5 Comparison between numerical and experimental value of velocity
3 结果与分析
为减少上下游边界条件引起的影响,选取位于中间的第四个池室作为典型池室进行分析。现有研究表明[4],随着鱼道底坡坡度增大,池室内流态将由二维向三维转变,即纵向速度的变化无法被忽略。为了更直观的比较因此受到的影响,同时使流态具有代表性,因此取0.33 倍水深的近底层平面hb以及0.67倍水深的近表层平面hs作为研究对象开展系统分析。
3.1 不同坡度对流态的影响
上一池室的水流经过竖缝压缩,以射流形式进入下一池室,通过水流扩散与对冲消耗水体能量,改善池室内水流条件。池室中存在两种流动方式,一种是经过竖缝后,流速仍远大于适合鱼类洄游过程中休憩流速[12]的主流区,另一种则是主流在受到下游隔板和池室边壁影响分离而形成的左右两侧回流区。鱼类通过主流区的较大流速辨别方向以便上溯,而回流区则需要为其在洄游过程中提供良好的休息环境。不同坡度下hs平面水流流场如图6 所示。在各个坡度下,左右两侧均形成不同大小的低速回流区,当坡度继续增大,回流区面积在主流影响下逐渐减小。坡度为1.5%时,回流区面积占整个池室面积较大,约为55%。随着坡度变化引起的流速增大,主流弯曲程度增加,并开始挤压回流区,左侧供鱼类休憩的低速回流区的面积显著减小,此时近表层的流态不利于鱼类洄游[13]。受边壁的约束,坡度在6.67%与8.33%时的主流左侧流态变化不大,但流速有所增加。右侧回流区则在池室上游挡板与射流入射角度的影响下变化不明显。
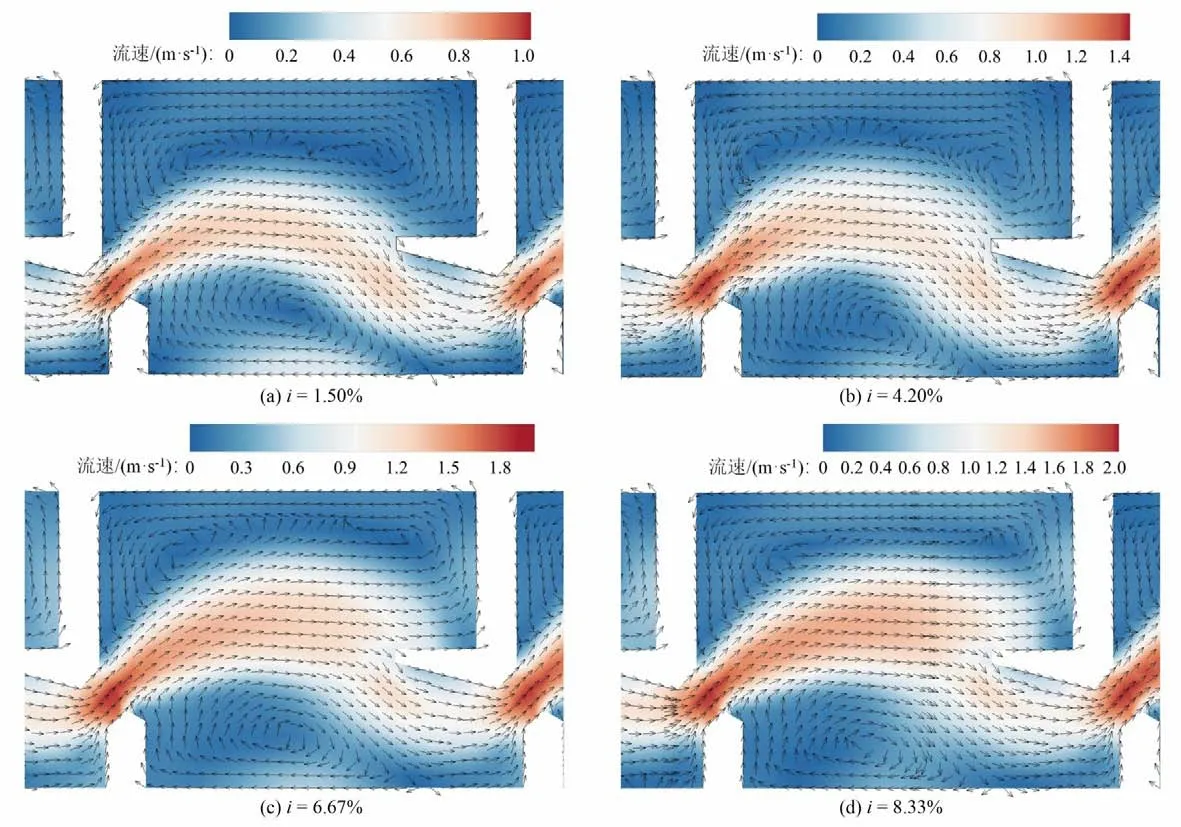
图6 4th池室内hs平面流速分布Fig.6 Flow velocity distribution of the hs plane in the 4th chamber
根据图7,坡度的增大对hb平面的流态影响并不明显。对比hs与hb两平面的流态,在1.5%与4.2%坡度下,hs与hb平面的流态相似。但对于6.67%坡度,两个平面流态之间存在显著差异,在hb平面中,主流在池室末端受钩状隔板的影响向右侧偏移,随后进入下一级池室,但是hs平面的流态却显示,几乎一半的主流进入了左侧的回流区,致使其左侧回流区面积减小了52.92%。而在8.33%的坡度中两平面流态差异与6.67%时相似。可以看到,在两个小于5%的坡度下,池室内流态呈现二维特性,但是之后的两种坡度中则出现了完全不同的现象,这与Wu等[4]的研究结果是一致的。
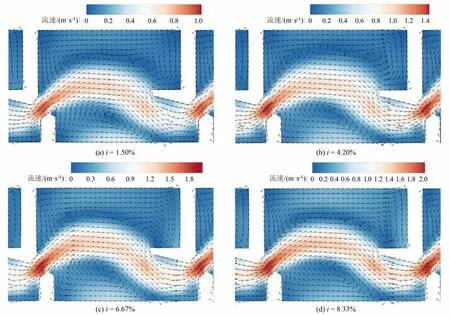
图7 4th池室内hb平面流速分布Fig.7 Flow velocity distribution of the hb plane in the 4th chamber
3.2 不同坡度对流速的影响
研究表明,作为影响鱼类洄游的关键因素之一,通过竖缝压缩后的高流速主流被鱼类感知,才能促使鱼类循着主流进入上游池室,同时,如果流速大于鱼类的爆发泳速,将导致鱼类难以洄游。模拟结果显示,池室内的最大流速出现在竖缝附近,并随着坡度增大而增大,在坡度为1.5%、4.2%、6.67%、8.33%坡度下,对应的竖缝附近最大流速分别为0.98、1.51、1.85、2.06 m/s。坡度的增大对池室内的流速变化的影响如图8 所示。主流区最小流速相差不大,主要是出现在主流区与回流区的交界处;而池室内最大流速在前3 个坡度中增加明显,分别为0.84、1.21、1.72 m/s,到8.33%时与6.77%坡度相比,其最大流速值仅增大8.1%,为1.86 m/s。主要是因为在此坡度条件下池室入口窄缝形成的射流流速增大,与受边壁约束的回流对冲更加激烈,因此能量耗散更多,导致8.33%坡度下的主流区最大流速增幅减小。
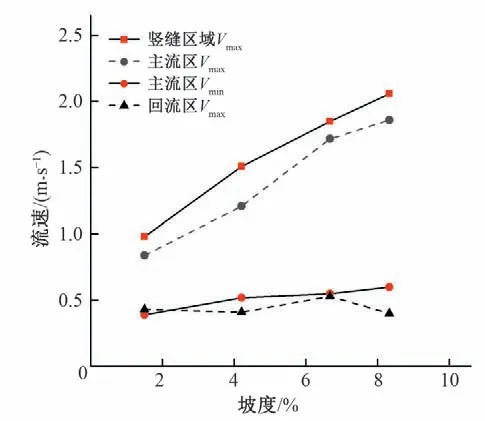
图8 池室流速变化Fig.8 Variation of flow velocity
由图6、7 可知,在1.5%和4.2%的坡度下,hs与hb平面的主流左侧均存在一定面积低速回流区,适合鱼类休憩,但是当坡度达到6.67%时,hs的一部分高流速在hb平面明显衰减,流态发生变化,最大流速由0.9 m/s 降低至0.2 m/s;由于隔板钩头对主流的约束而迫使其向右侧转向,部分主流因此进入右侧回流区,因此回流区最大流速主要出现在主流右侧靠近边壁的区域。随着坡度增加,主流区在池室内的面积逐渐增大,高流速主流带动回流促使池室内平均流速增加,意味着鱼类在洄游过程中将消耗更多的能量,且适合休憩的低速回流区也进一步减少,即使一些鱼类能够通过大坡度下的高流速竖缝,也可能无法找到合适的低流速区休憩,进而降低过鱼效率。
3.3 不同坡度对紊动能的影响
不同坡度下紊动能在鱼道典型池室内的分布如图9、10 所示。Marriner 等[12]认为,池室内大部分区域的紊动能应该保持在0.05 m2/s2,否则会影响鱼类洄游。结果显示,在鱼道结构的消能作用下,竖缝附近的高紊动能均得到有效衰减,即使在8.33%坡度时,紊动能也能在较短距离内减少至0.05 m2/s2以下。随着坡度增大,高紊动能的范围均有明显增加。当坡度为1.5%与4.2%时,hs与hb平面的紊动能分布类似,在竖缝附近出现最大值,并沿着水流衰减,之后在隔板钩头的前侧再次出现极大值。而6.67%和8.33%坡度下hs与hb两平面的紊动能分布均出现了明显差异,hs平面中的极大值出现在了距离隔板钩头更偏左的位置,其原因主要是由于受隔板钩头的分离,几乎一半的主流进入了左侧,因此紊动能的分布出现了偏移。同时,紊动能在池室内也因此更加分散,高紊动能区域较hb平面更少。

图9 4th池室内hs平面紊动能分布Fig.9 TKE distribution of the hs plane in the 4th chamber
表3 展示了4 种坡度条件下的各平面最大紊动能与平均紊动能。随着坡度的增加,紊动能的最大值与平均值均逐渐提升。相较于两个较小坡度,6.67%与8.33%的最大紊动能差值明显增加,hb平面的最大紊动能分别比hs增大9.2%和21.0%,受坡度变化的影响较大。池室内平均紊动能较为理想,最大值为0.035 1 m2/s2,出现在8.33%坡度下的hb平面。

表3 池室最大紊动能与平均紊动能Tab.3 The maximum TKE and average TKE
4 结论
利用数值模拟系统开展不同坡度对池室内水力特性影响的研究,重点对鱼道池室内流速和紊动能分布规律展开分析,得到结论如下。
(1)随着鱼道坡度增加,hs的回流区受射流挤压范围减小,由最初的55.11%下降到15.22%,左侧回流区的显著减小,对于鱼类在洄游过程中休憩十分不利。hb平面的流态则受坡度影响较小,变化不大。
(2)hs与hb平面在坡度为1.5%与4.2%时,流场受影响较小。但当坡度增大到6.67%,由于高速主流的汇入,相比于hb平面,hs平面的低速回流区面积明显减小,特别是左侧回流区减少了近20%,流速与流态的同时改变体现了较大坡度下的三维特性。

图10 4th池室内hb平面紊动能分布Fig.10 TKE distribution of the hb plane in the 4th chamber
(3)竖缝处最大流速随坡度增加,在8.33%时超过2 m/s;主流区与回流区的流速差逐渐增大;主流区最大流速从0.84 m/s增至1.78 m/s,而最小流速与回流区最大流速则受坡度影响较小。
(4)相较于两种较大坡度,1.5%与4.2%时的紊动能大小及其分布更适合鱼类洄游。hs平面中由于主流的分散,在较大坡度下不适合鱼类洄游(大于0.05 m2/s2)的高紊动能区域较hb更少。同时平均紊动能随坡度增大而增大,在坡度为8.33%时最大值为0.035 1 m2/s2。
