Ti2AlNb 合金的嵌入原子势*
2022-10-27刘杰刘艳侠
刘杰 刘艳侠
(辽宁大学物理学院,沈阳 110036)
分子动力学模拟是一种行之有效的计算机模拟方法;然而,由于缺少合适的多元合金原子间势,因而限制了分子动力学模拟的应用.多元合金原子间势的开发一直具有挑战性.本文在嵌入原子势模型的框架下,提出一种适用于三元有序合金的原子间势构建方法,并开发了适用于原子尺度力学行为模拟的Ti2AlNb 合金新型原子间势.该势能够很好地再现B2-Ti2AlNb 的弹性常数、未弛豫的空位形成能、置换原子形成能、换位原子形成能、表面能和三种有序构型(B2 相、D019 相、O 相)在不同体积下的内聚能.为了进一步检验势函数,计算了B2 相的E-V 曲线,结果与Rose 曲线符合得很好;利用分子动力学模拟研究了B2 相的熔化转变过程,结果大致反映了实验情况.本文的工作一方面为开发多元合金原子间势提供一种途径,另一方面为模拟计算Ti2AlNb 合金的工作者提供一种选择.
1 引言
目前开发原子间势主要有两类方法: 一类是近几年发展起来的机器学习法[1];另一类是传统的拟合原子间势参数的方法.
随着人工智能的快速发展,机器学习法开发原子间势应用而生,已经有许多成功应用的案例[2,3],Smith等[4]在2020 年用机器学习的方法构建了铝元素的原子间势,他们应用了多种神经网络来训练大量数据,比如由金属的不同结构的多种性质,最后得到了计算精度非常高的原子间势.机器学习法构建原子间势的优势在于减少了人为干预的成分,规避了传统方法建势的参数化问题,且可以达到与第一原理方法相媲美的精度[5].但是机器学习势的非物理形式阻碍了对模型参数的直接解释,并阻止了对参考数据集没有很好描述的构型空间区域的外推,同时机器学习势需要准备大量准确的训练数据集.
传统方法构建原子间势也同样具有一定的优势,首先构建的势函数形式简单,与分子动力学接口友好,需要准备的拟合数据数量远少于机器学习势,加之人工特有的跨学科优势,拟合过程中可根据物理理论进行人为干预,可以更加灵活地调整参数,且拟合过程中的每一步都具有清晰的物理意义.
Ti2AlNb 合金具有很多优异性能,如高强度、高比模量以及较高的抗氧化性等[6-9],使其成为航空航天发动机的首选材料之一.关于Ti2AlNb 合金的实验研究,可采用掺杂、多种强化机制及热处理等工艺来改善合金的使用性能[10].理论研究主要采用第一原理计算的方法.如Pathak 和Singh[11]用第一原理方法计算了三种有序构型(B2 相、D019相、O 相)结构的稳定性,并给出了各自的晶体结构、空间群、原子坐标等信息.
由于缺少合适的Ti2AlNb 合金原子间势,因而限制了使用分子动力学模拟的方法研究Ti2AlNb合金的性能.Ti2AlNb 基合金一般由α2,O,B2 中的两相或三相构成.β/B2 都是bcc 结构,β是无序相,B2 是有序相.Nb是β相的稳定元素,由于Ti2AlNb 基合金中Nb 含量比较高,所以β相稳定元素一直存在,且B2 相滑移系较多,是塑性相,因此,本文采用传统方法主要针对B2 相开发Ti2AlNb合金原子间势,期望能为分子动力学模拟工作者提供一种选择.
2 原子间势的构建
2.1 模型
本文选用嵌入原子 (embedded-atom method,EAM)势模型[12],在该模型下体系的总能为
其中α,β,γ,ϵ,σ,μ为拟合参数;rc为截断距离;h为截断函数形状的调整参数,截断函数形式为
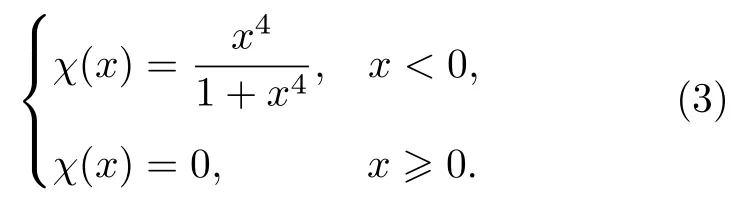
对于本文的三元合金原子间势的构建,需要拟合三种交叉对势,分别为ϕ(rTiAl),ϕ(rTiNb)和ϕ(rNbAl),包含18 个拟合参数,再加上sx和gx(下标x表示Ti,Al,Nb 的任意一种元素),共24 个拟合参数,截断距离选用相同的值为rc.
在拟合合金的原子间势时,应用了关于以下规范变换的不变性[14,15]:
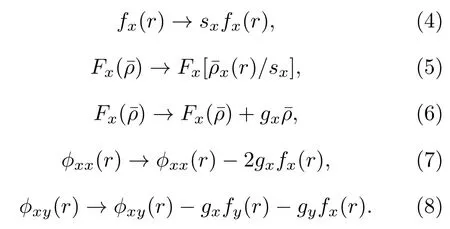
x和y代表Ti,Al,Nb 三种元素中的任意一种,上述变换中sx和gx是任意常数,对于三元有序构型比如B2-Ti2AlNb 合金,不是严格意义满足能量对其公式变换的不变性(本质上这种变换关系对于合金需要满足高度有序的对称性,规范变换会改变势函数的形状).对于A-B-C 体系,可以使变换后的多体势满足[14],这样多体势函数就可以在平衡状态下对应原子的电子密度处取得极值(通常情况下为极小值)[16],本文在B2 相的环境中使其满足的值由归一化条件确定,此外本文尽量使和的值接近1.
2.2 拟合数据库
关于Ti2AlNb 合金性能的实验值非常有限,因此本文主要使用第一原理计算的数据来参数化原子间势.使用基于密度泛函理论的VASP 软件(Viennaab-initiosimulation package),交换关联泛函选择Perdew-Wang 91 形式,平面波截断能为500 eV,总能收敛标准为10—5,原子弛豫最大步数为100,采用共轭梯度算法(CG 算法)优化原子的位置,k点选取因晶体结构的差异和计算物理量的不同而略有不同.本文用于拟合的数据库包括:B2 相的晶格常数如表1 所列;三种纯金属Ti,Al,Nb 的内聚能,如表2 所列;B2 相的弹性常数如表4 所列;B2 相的未弛豫的单空位形成能和双空位形成能如表5 所列;B2 相的置换原子形成能和换位原子形成能如表6 所列;B2 相的内聚能如表8 所列.
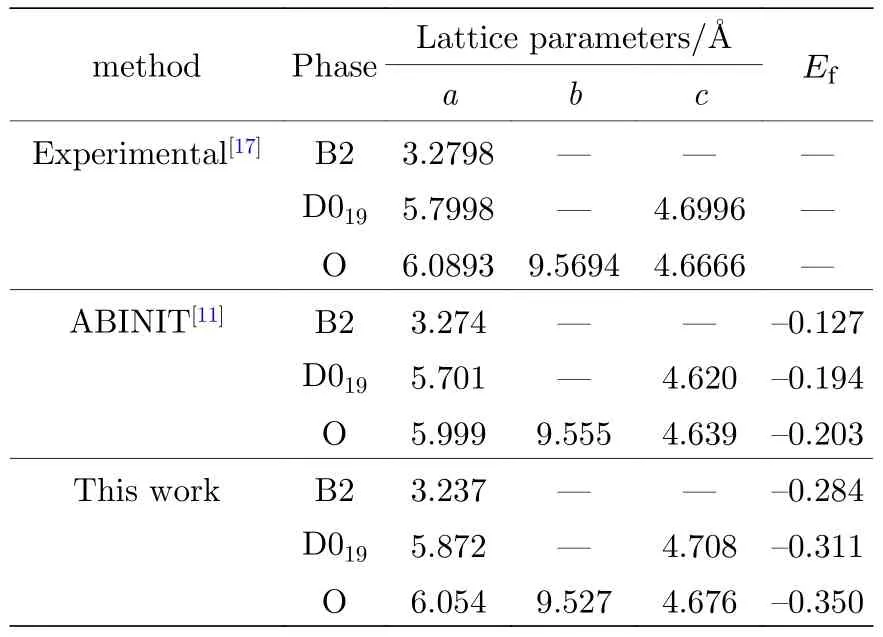
表1 B2-Ti2AlNb 的晶格常数和生成焓(单位: eV)Table 1.Lattice constants and formation enthalpy for B2-Ti2AlNb (in eV).
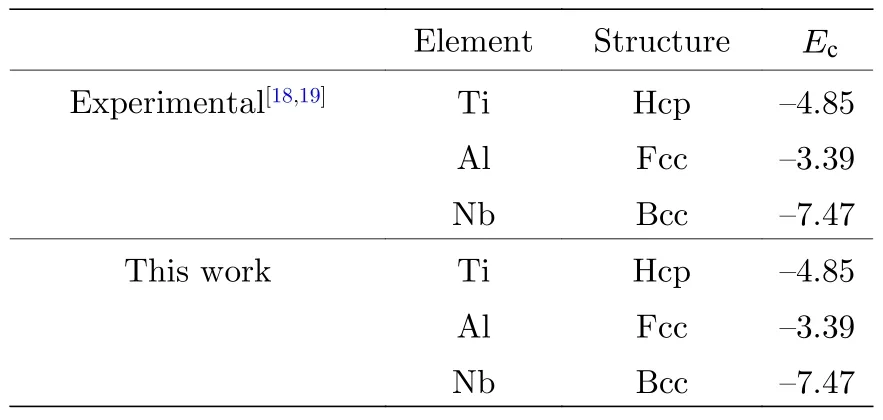
表2 单质Ti,Al,Nb 的内聚能(单位: eV)Table 2.Cohesive energies for Ti,Al and Nb (in eV).
表1 中同时列出了实验值和文献[11]的计算结果,可以看出,本文的计算结果与实验值和文献[11]的结果都非常接近.
2.3 原子间势函数参数化
为了对原子间势函数进行参数化,以及检验原子间势的质量,需要使用原子间势表示各个物理量.本文考虑了长程相互作用,原子间势的截断距离设置在第六和第七近邻之间,且需要给出Ti,Al,Nb 三种元素之间的对势及电子云之间的相互作用,因此解析表达式比较复杂.为此本文主要通过程序设计来建立物理量与原子间势的关系.设计思想是,先建立原子构型模块,包含原子空间坐标、原子类型和原子编号等信息,然后在此基础上,根据相应的理论进行各种物理量的计算.这里只介绍本文使用的弹性常数和空位形成能的计算公式.
根据弹性理论,可以得到平衡状态下弹性常数与原子间势之间的关系为[20]
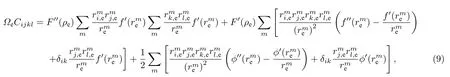

根据(1)式,可以得到平衡状态下空位形成能与原子间势的关系式为[21]
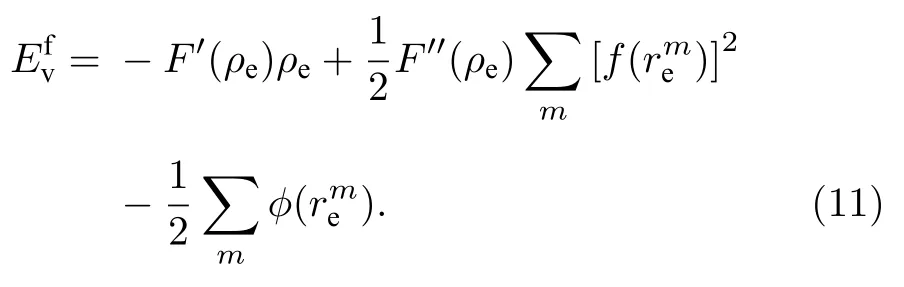
在确立了物理量与原子间势的关系和拟合数据库之后,利用能量最小化的方法,同时考虑了物理量的权重,拟合了原子间势函数的参数,如表3 所列.
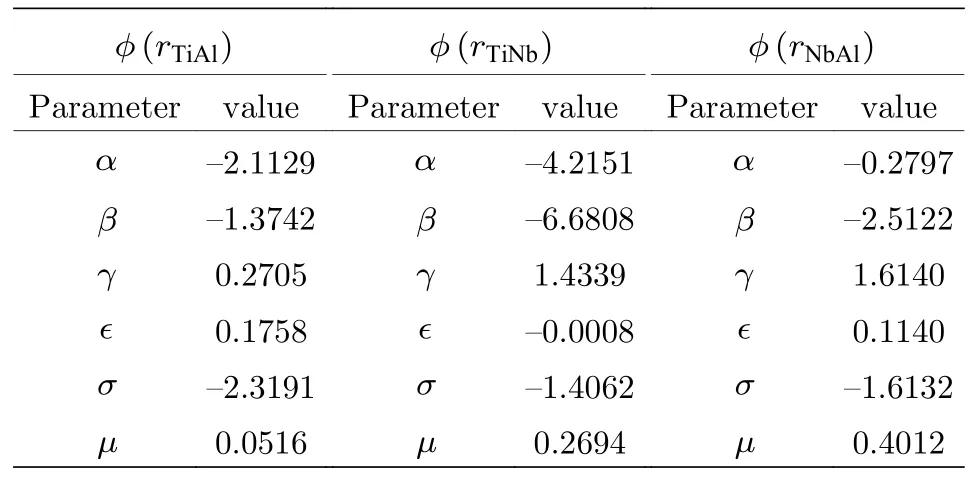
表3 Ti2AlNb 合金EAM 势的拟合参数Table 3.Fitting parameters of EAM potential for Ti2AlNb alloys.
在拟合之前,已将B2 相构型中的Ti 原子的背景电子密度归一化,由此将限制sTi,sAl,sNb三者之间的关系,为了确保电子密度函数曲线在x轴上方,在拟合过程中已限制三者的符号均为正.对于Ti 原子,在电子密度归一点处嵌入能函数达到最低点,而对于Al 和Nb 原子而言,在拟合过程中尽力使其接近1.其中参数sTi,sAl,sNb的值分别为0.3333,0.4646,4.1557,参 数gTi,gAl,gNb的值分别为—7.3047×10—7,—0.0640,—0.6733,由此可以得到EAM 型原子间势的各函数如图1 所示.
3 结果与讨论
作为对原子间势的测试及应用,利用开发的Ti2AlNb 合金的EAM 势研究了B2-Ti2AlNb 的弹性常数、点缺陷、表面能、熔点性能,以及Ti2AlNb合金三种有序相的E-V关系.
3.1 弹性常数
B2-Ti2AlNb 晶胞的空间点阵属于正方晶系,其晶格常数满足a=b≠c,α=β=γ=90°,弹性常数[22]满足C11=C22,C55=C66,C13=C23,计算比较了B2 相的6 个弹性常数(C11,C33,C44,C55,C12,C13),利用本文开发的EAM 势和第一原理的计算结果如表4 所列.
由表4 可以看出,本文开发的EAM 势的计算结果与第一原理(DFT)计算结果基本一致.
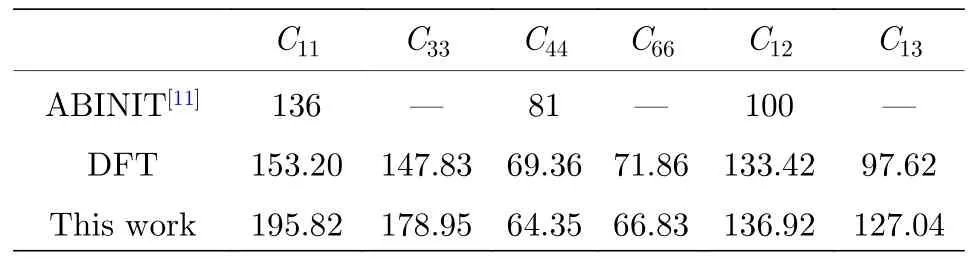
表4 B2-Ti2AlNb 的弹性常数(单位: GPa)Table 4.Elastic constants for B2-Ti2AlNb (in GPa).
3.2 空位形成能
单空位及双空位形成能[23]的计算方法分别为:
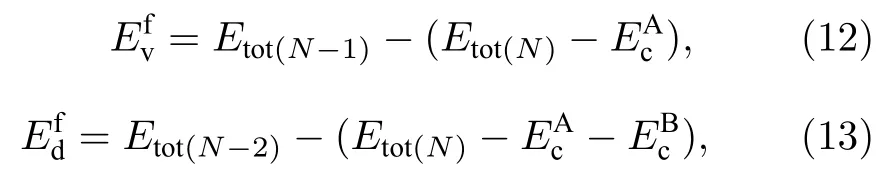
其中,Etot(N)表示理想超胞总能,Etot(N-1)表示去掉一个原子的超胞总能,Etot(N-2)表示去掉两个原子的超胞总能,和分别表示去掉的单质原子A 和原子B 的内聚能.本文所有关于空位形成能的计算结果均列于表5 中,表5 中第二列表示去掉的原子类型,后面的数字表示第几近邻,例如AlNb-1 表示去掉超胞中最近邻的Al 和Nb 两个原子.
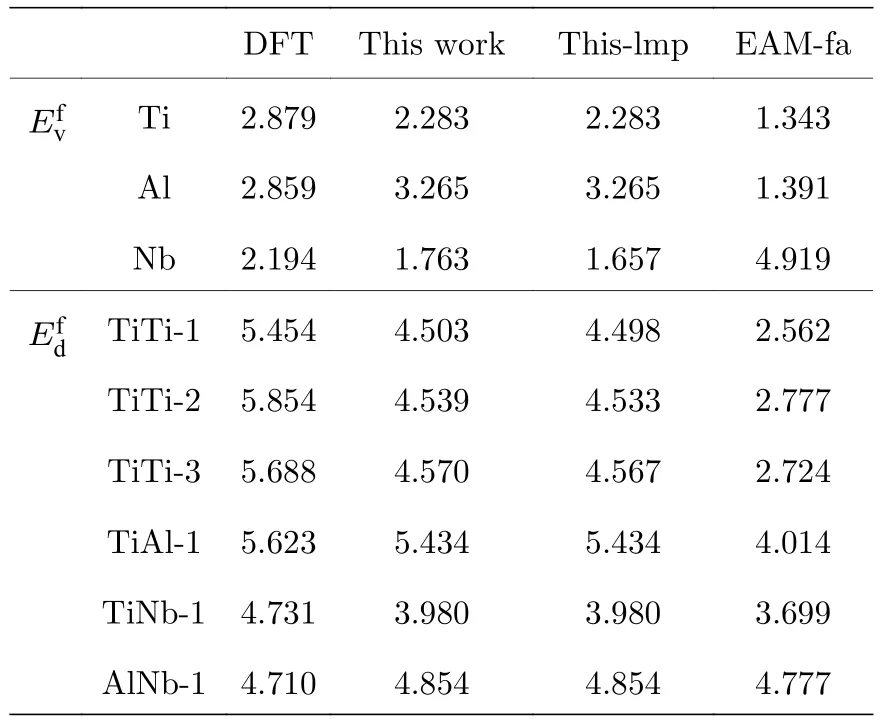
表5 B2-Ti2AlNb 单空位形成能和双空位形成能(单位: eV)Table 5.Mono-vacancy formation energies and divacancy formation energies for B2-Ti2AlNb (in eV).
表5 中标注“This work”这一列的值是利用本文开发的EAM 势编程计算得到的,标注“Thislmp”的这一列表示利用本文开发的EAM 势,使用Lammps 软件进行模拟计算的结果.标注“EAM-fa”这一列表示本文利用Farkas[24]开发的EAM 势的计算结果,计算工具使用的依然是Lammps 软件.由图2 所示的空位形成能的对比图可以看出,本文开发的EAM 势,用两种方法的计算结果几乎完全一致,相比于用Farkas[24]的势整体上更接近第一原理计算结果.
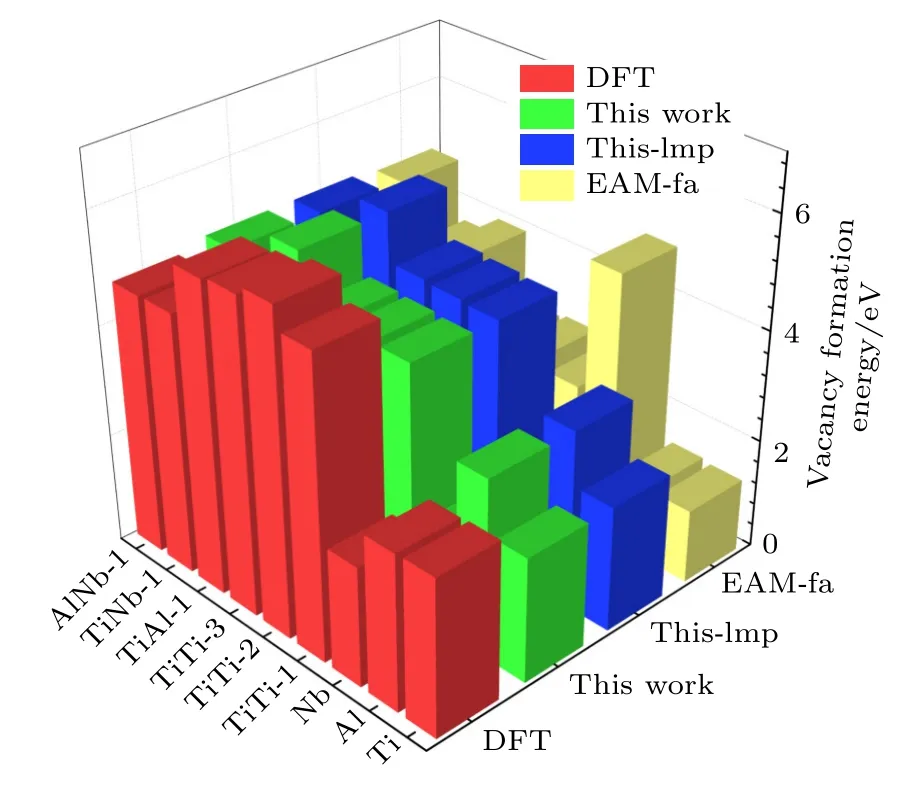
图2 B2-Ti2AlNb 单空位形成能与双空位形成能Fig.2.Mono-vacancy formation energies and di-vacancy formation energies for B2-Ti2AlNb.
3.3 置换和换位原子形成能
利用本文开发的EAM 势计算了B2 相的置换原子形成能,同时计算了截断距离范围内交换原子位置的形成能,即换位原子形成能.在图3 中已经清晰地表示出原子换位及其表征情况,其中红色、绿色、蓝色的原子分别表示Ti,Al,Nb.置换原子形成能为
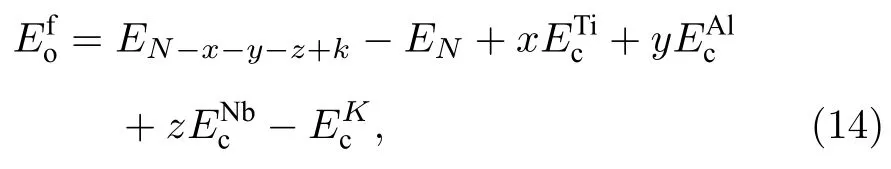

图3 B2-Ti2AlNb 原子位置换位示意图Fig.3.Atom position transposition diagram for B2-Ti2AlNb.
EN-x-y-z+k表示有缺陷的超胞总能,EN表示理想超胞的总能,表示单质Ti,Al,Nb,K原子的内聚能,K表示用于置换的原子的类型.x,y,z的值可以是0 或±1,分别表示被置换原子Ti,Al,Nb 的数目,k表示用于置换的原子的数目.例如满足x=z=0,y=1,K=Ti 的组合表示在Al 原子的点阵上置换一个Ti 原子,用(T iAl)表征,其他置换原子的形成能也采用这种表征方式.对于换位原子的形成能可表示为
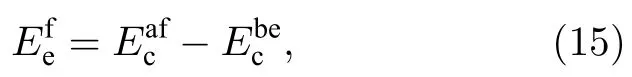
式中表示换位后超胞的总能,表示理想超胞的总能.
从表6 可以看出,本文开发的EAM 势计算的多种置换原子和换位原子的形成能更接近第一原理计算结果,从图4 和图5 可以更清晰地看到这一结果,与第一原理相比,各种形成能的误差最大也没有超过0.233 eV,表明该EAM 势能很好地描述Ti2AlNb 合金的点缺陷性质.
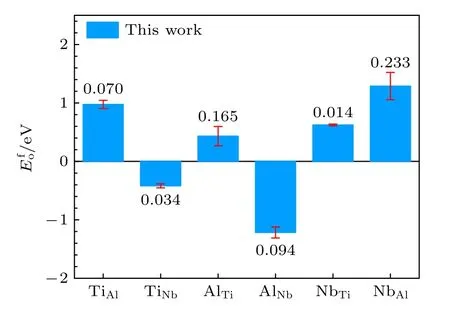
图4 B2-Ti2AlNb 置换原子形成能的误差Fig.4.Deviations of substitutional atom formation energies for B2-Ti2AlNb.
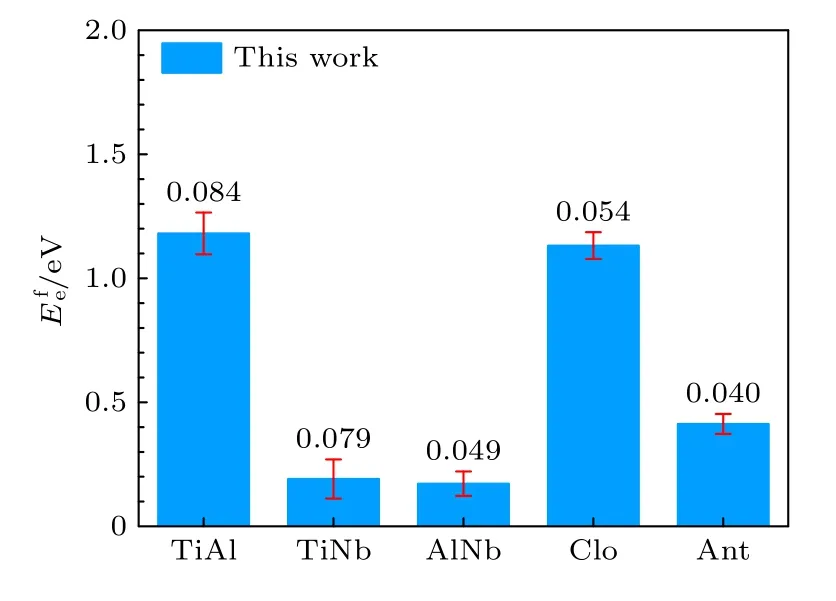
图5 B2-Ti2AlNb 换位原子形成能的误差Fig.5.Deviations of transposition atom formation energies for B2-Ti2AlNb.
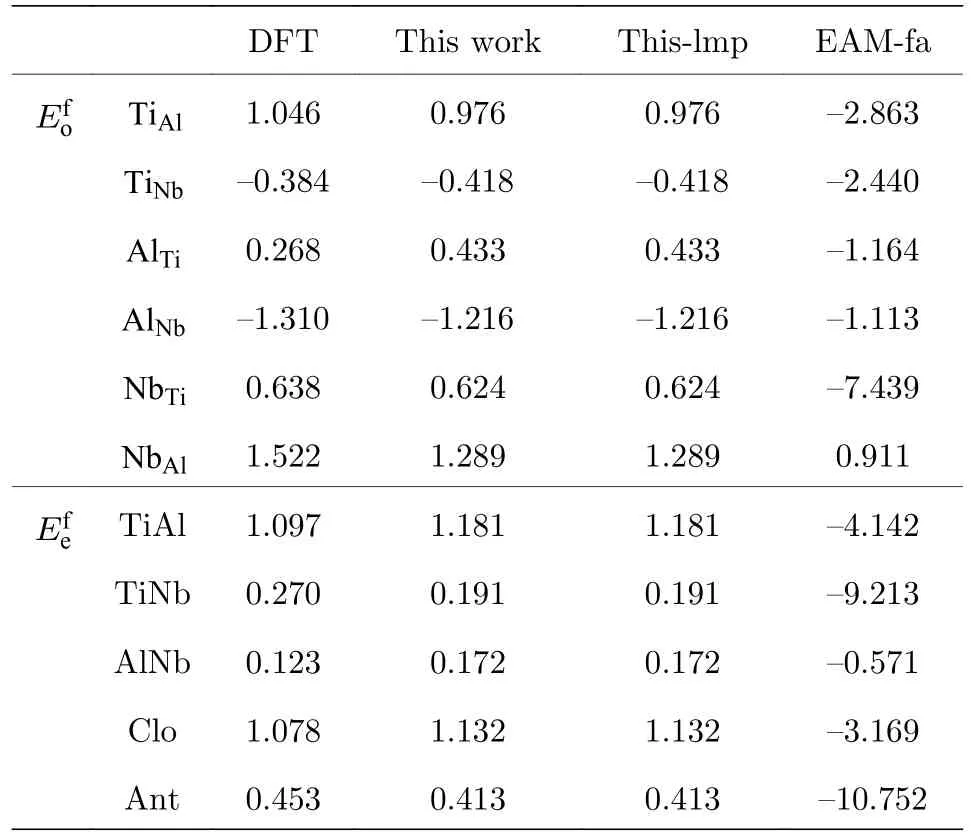
表6 B2-Ti2AlNb 置换原子和换位原子形成能(单位: eV)Table 6.Substitutional atom and transposition atom formation energies for B2-Ti2AlNb (in eV).
3.4 表面能
平衡态下,理想晶胞中的原子受周围原子作用的合力为零,处于能量最低的状态,但位于表面上的原子所受的周围原子的合力不为零,因而能量较高,减去没有表面时体系的能量再除以该表面的面积,即为该表面的表面能,表面能的计算公式为
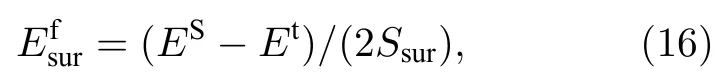
式中为表面能;ES表示具有表面时体系的总能;Et表示没有表面时体系的总能;Ssur为体系中形成表面的面积.本文计算了B2 相中(100)面和(110)面的表面能,形成表面的体系在平行于表面的方向上利用了周期性边界条件,在垂直于表面的方向上设置了扩胞和真空层,具体的计算结果如表7 所示,表7 中标记一撇“'”的表面表示对该表面进行了能量最小化.从表7 中可以发现本文开发的EAM 势关于(100)和(110)两表面能的计算结果与第一原理计算结果趋势一致,都表明(110)面的表面能更小.
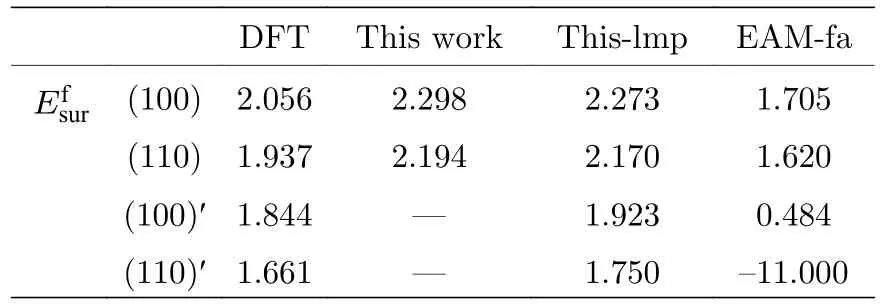
表7 B2-Ti2AlNb 的表面能(单位: eV)Table 7.Surface energies for B2-Ti2AlNb (in eV).
3.5 E-V 曲线
为了检验原子间势偏离平衡态时的表现,利用本文开发的EAM 势推导了Ti2AlNb 合金三种有序相的E-V关系.考虑到合金中Ti,Al,Nb 三种原子的周围环境不同,因此计算了分别以Ti,Al,Nb 三种原子为参考原子的E-V关系,合金中以Ti 原子为参考原子的E-V关系为
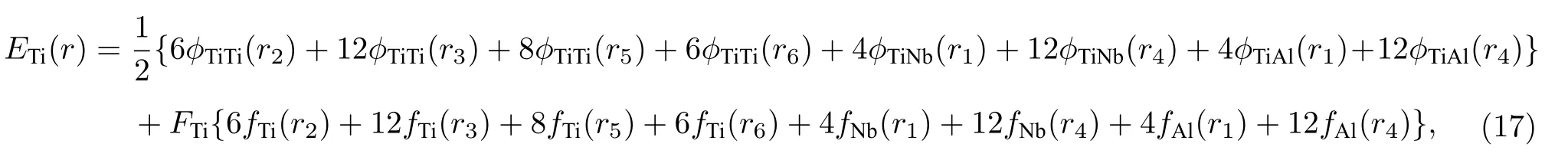
式中,r1表示B2 相合金中最近邻距离,r2表示次近邻距离,以此类推,rn表示第n近邻距离.电子密度函数fTi(rn) 表示为第n近邻的Ti 原子贡献的电子密度,前面的数字表示该原子的数目.
同理,可以得到分别以合金中Al 原子和Nb 原子为参考原子的E-V关系为
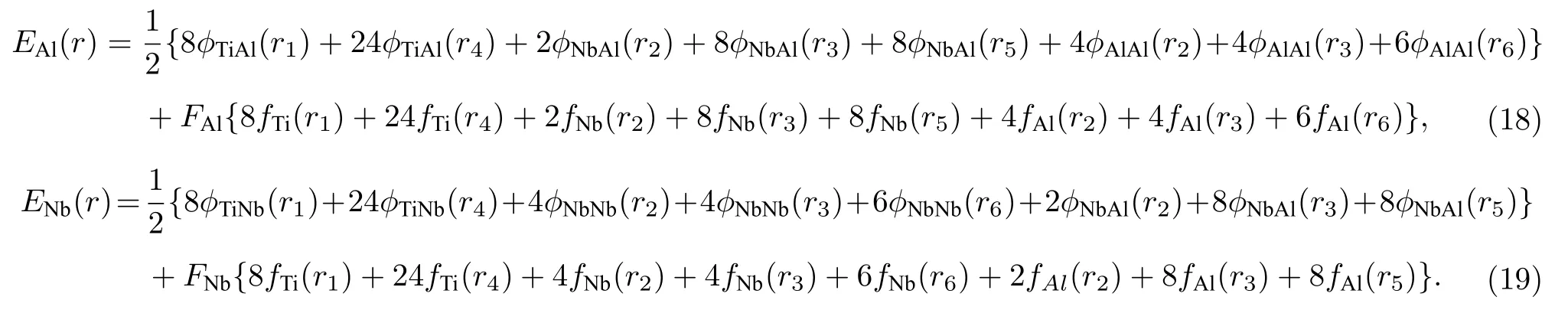
对上述三种E-V关系进行加权平均,便可得到Ti2AlNb 合金中平均每个原子的E-V关系,如(20)式所示:
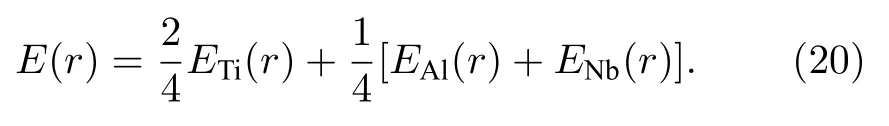
本文计算的B2相E-V关系曲线如图6 所示,同时为了比较,根据Rose 的经验公式[25]计算了E-V关系,同时画在图6 中.
由图6 可以看出,在距离小于约3.3 Å的范围内拟合曲线与Rose 曲线吻合非常好,同时表明曲线在体系处于平衡状态时的曲率相近,弹性模量一致.超过这个范围两曲线虽然略有差距,但整体变化平稳,没有出现过多的振荡.
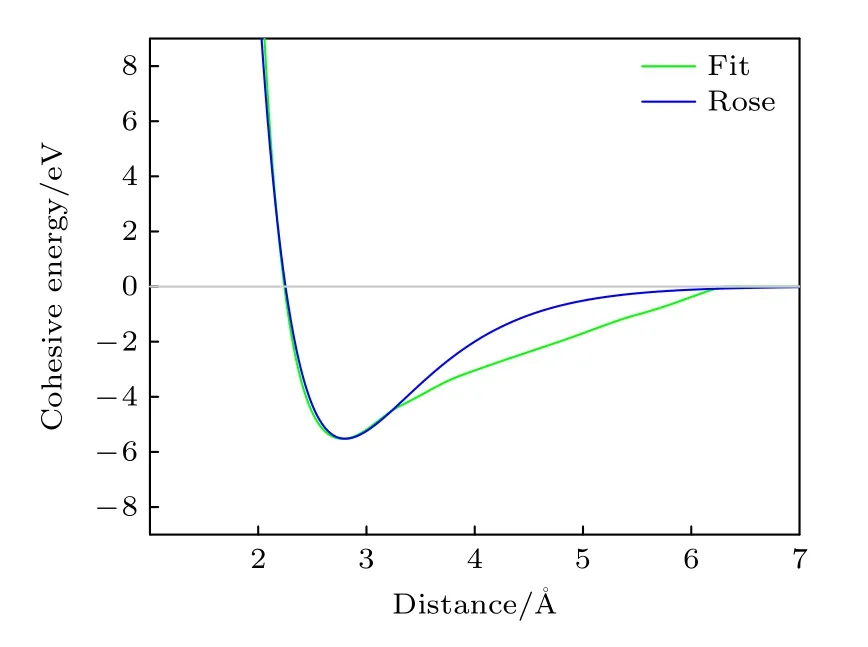
图6 B2-Ti2AlNb的E-V 曲线与Rose 曲线Fig.6.E-V curve and Rose curve for B2-Ti2AlNb.
为了验证本文开发的EAM 势对于Ti2AlNb合金不同相的描述能力,使用第一原理方法计算了平衡状态下B2 相、D019相、O 相在不同体积下的内聚能,计算结果见表8,三种有序相的E-V曲线如图7 所示.从图7 可以发现: 对于B2 相,该EAM 势的计算结果非常接近第一原理的计算结果,Farkas[24]的结果在体积膨胀超过20% 时变化非常缓慢,不太适合这个范围;对于D019相,本文的EAM 势的计算结果相比Farkas[24]的计算结果更接近第一原理计算结果;对于O 相,本文的结果不仅与第一原理的结果的趋势完全一致,偏差也非常小,Farkas[24]的结果与第一原理的计算偏差也不大,而且曲线的左侧,即当晶体被压缩时,Farkas的结果与第一原理的结果趋势也完全一致,但是曲线右侧的变化趋势与第一原理计算结果不太一致,也就是当晶体膨胀时,Farkas 的结果比第一原理的结果变化缓慢.
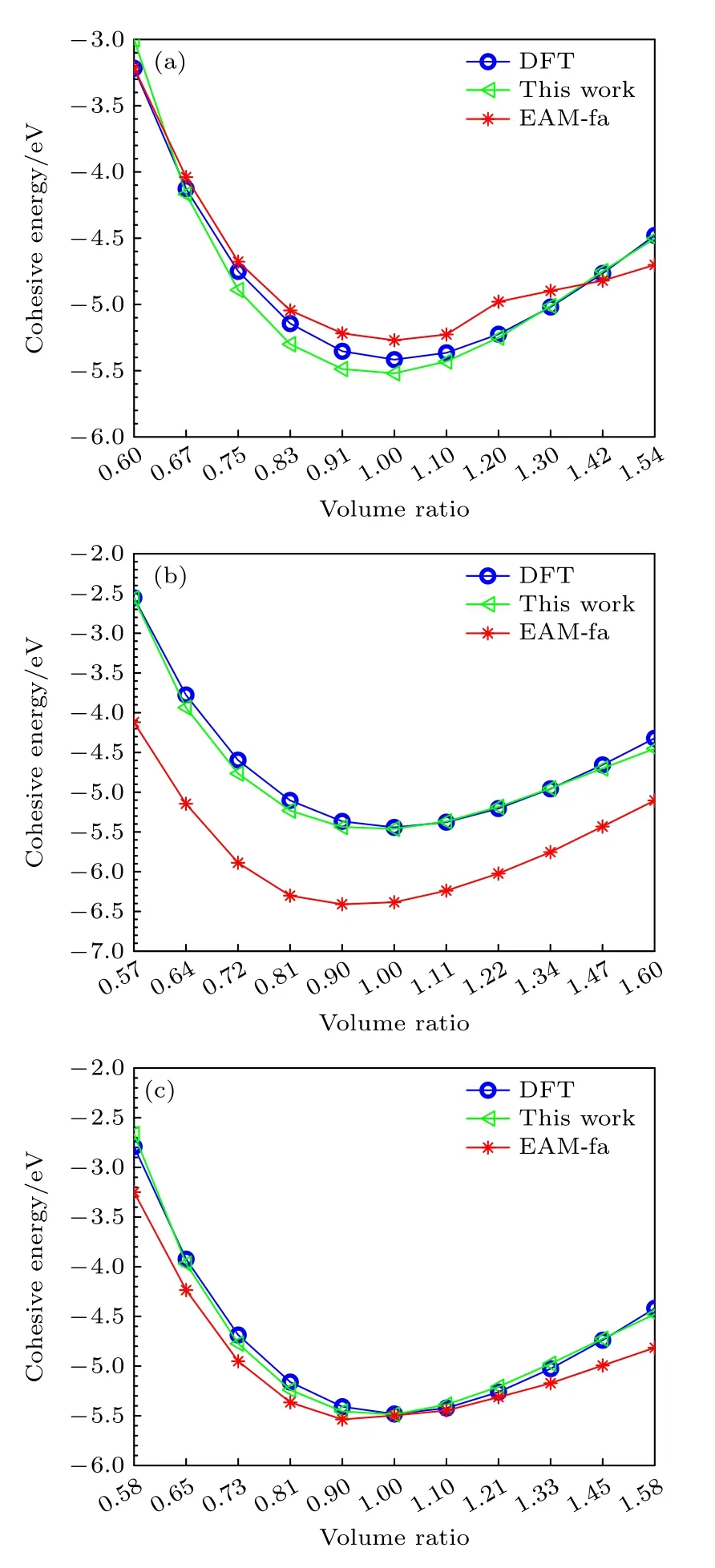
图7 Ti2AlNb 合金的E-V曲线 (a) B2 相;(b) D019 相;(c) O相Fig.7.E-V curve of Ti2AlNb alloys: (a) B2 phase;(b) D019 phase;(c) O phase.
3.6 熔点
利用本文开发的EAM 势通过分子动力学模拟研究了B2 相的熔化转变过程,模拟盒子的大小为3456 个原子的超胞,在初始B2 相构型下保持初始温度,并在NVT 系综下进行弛豫,升温的过程在NPT 系综下进行,期间原子体积在0 至1400 K 附近的温度范围内呈线性增加,如图8 所示.图8中可以看出B2-Ti2AlNb 合金在1400 K附近发生一级相变,单位体积发生突变,正如图9 所示,体系在此温度附近前后从有序构型转变为无序状态.图9 中红色、绿色、蓝色的原子分别表示Ti,Al,Nb.
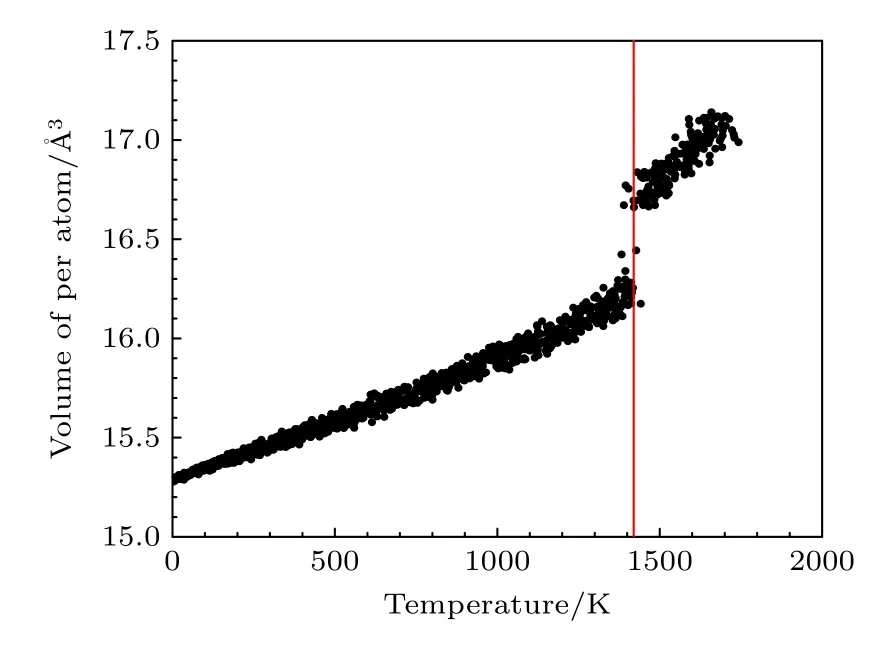
图8 B2 相的每个原子的体积随温度的变化Fig.8.Volume variation of each atom for B2 phase as functions of temperature.
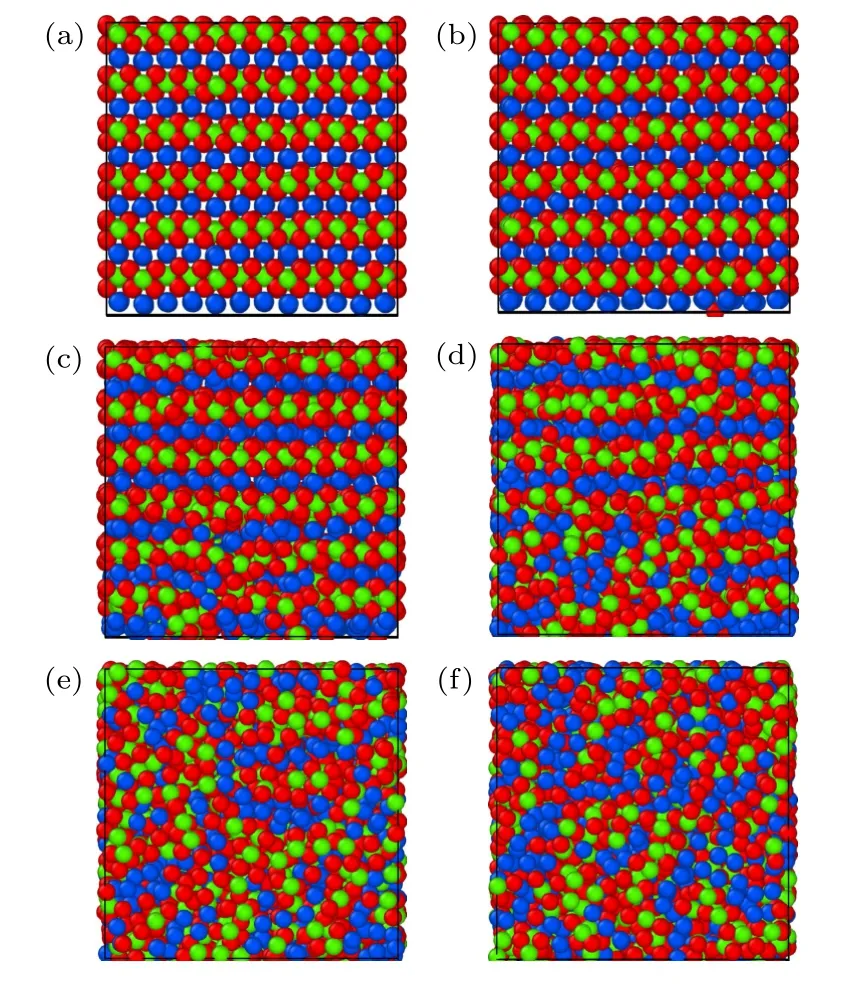
图9 B2 相随温度变化的截面快照 (a) 296 K;(b) 754 K;(c) 1428 K;(d) 1390 K;(e) 1449 K;(f) 1728 KFig.9.Cross-section snapshots for B2 phase as functions of temperature: (a) 296 K;(b) 754 K;(c) 1428 K;(d) 1390 K;(e) 1449 K;(f) 1728 K.
从Ti-Al 平衡相图[26]中看出,Ti3Al 合金的熔点大于1900 K,向Ti3Al 基合金中掺杂Nb 可以提升合金的综合性能,而Ti-22 Al-26 Nb 合金B2 相的熔点大约为1873 K[27],以此为参考,利用本文开发的EAM 势计算的Ti2AlNb 合金的熔点比此温度低了约25%.由于本文主要针对Ti2AlNb 合金的力学性能开发EAM 势,拟合数据库中未包含与温度相关的数据.一般来说,同一种势函数形式很难同时描述低温和高温的性能,考虑有两种改进方案,一是在拟合数据库中加入相变等与温度相关的数据,在保证不影响对力学性能描述的基础上,改善势函数描述高温性能的能力;另一种是针对高温性能开发新的原子间势,只用于预测高温性能.
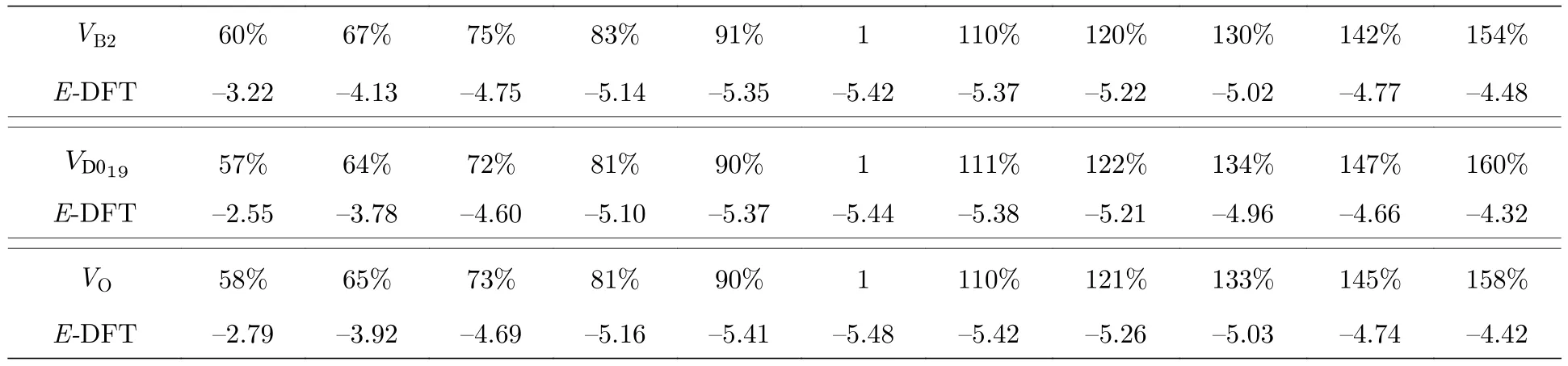
表8 Ti2AlNb 合金的内聚能(单位: eV)Table 8.Cohesive energies for Ti2AlNb alloys (in eV).
4 结论
本文使用传统方法开发了Ti2AlNb 合金的EAM 势.主要采用静态计算和分子动力学模拟两种手段考察了本文开发的EAM 势的质量.
1) 静态计算表明,该EAM 势很好地再现了B2相Ti2AlNb 合金的弹性常数、内聚能和多种缺陷形成能,能很好地描述Ti2AlNb 合金B2 相、D019相、O 相的E-V系.其中B2 相的E-V关系在近距离约3.3 Å以内与Rose 曲线符合的非常好.
2) 利用Lammps 软件模拟计算了B2-Ti2AlNb合金的各种空位形成能,计算结果均与第一原理计算结果符合得很好.置换原子形成能和换位原子形成能计算结果与第一原理结果相比,其大部分缺陷形成能的误差均在0.100 eV 以下,对于Al 原子置换Ti 原子的置换原子形成能,误差在0.165 eV 之内,Nb 原子置换Al 原子的置换原子形成能,误差在0.233 eV 以内.利用Lammps 软件模拟计算了B2 相Ti2AlNb 的表面能,计算结果表明B2 相的(110)面比(100)面更稳定,表面能更低,与第一原理的计算结果一致.
3) 利用Lammps 软件模拟研究了Ti2AlNb 合金B2 相的熔化转变过程,熔点的模拟结果大约为1400 K,低于实验结果.主要由于开发势函数的拟合库中未包含与温度、相变相关的物理量.
本文开发的Ti2AlNb 合金的EAM 势在描述B2 相的弹性性能,点缺陷性能、表面能及E-V关系性能方面的能力较好,预测可用于与这些性能相关的力学性质方面的研究.
