含水率对高地应力炭质板岩隧道围岩稳定性的影响研究

2022-10-26胡涛涛葛峻恺刘可萌

水资源与水工程学报 2022年5期

胡涛涛，葛峻恺，刘可萌

(长安大学公路学院，陕西西安 710064)

1 研究背景

在高速铁路、高速公路和城市地铁的建设中，受地形和地质状况多样性和不确定性的影响，隧道工程常常是整个工程项目的代表性和控制性工程，尤其是在偏远的西部地区和岩溶地区，因其地势起伏大、地质地貌复杂，各类岩土体存在不同发育程度的结构面、裂隙面甚至是软硬互层，使得岩体表现出较大的力学差异，增加了隧道工程的施工难度[1-4]。高地应力软弱围岩强度较低，尤其是在地下水较为丰富的地带，在水的软化作用下，围岩承载能力和自稳能力大大降低，导致该地段在施工过程中易出现塌方、大变形、支护结构扭曲侵限等问题[5-9]，因此研究富水软弱围岩隧道的受力特性显得尤为重要。

针对软弱围岩隧道在富水条件下的受力特性，国内外有关研究人员进行了较为广泛深入的研究。宋勇军等[10]对兰渝铁路木寨岭隧道炭质板岩进行了干燥与饱水状态下的蠕变实验，结果表明水对岩石瞬时变形的影响主要表现在瞬时塑性应变方面；在蠕变变形方面，水对岩石黏弹性影响显著。左清军等[11]针对油坊坪隧道跨越断层段遭受的塌方问题，总结隧道宏观变形演化历史，分析了跨越断层富水软岩隧道塌方的影响因素及围岩失稳破坏模式。刘聪等[12]以港沟隧道穿越断裂破碎带区域为依托工程，研究了富水地层超大断面隧道施工情况下围岩力学响应特征。刘涛等[13]对围岩在静水及地下水情况下的稳定性及变形控制对策进行数值模拟分析，并通过现场试验、监测及分析，论证特定预加固方案对变形控制的有效性。针对隧道软岩层中含有弱夹层问题，Liu等[14]和Zhang等[15]通过基于围岩位移场的微缩模型试验，分析了软岩层中具有潜在弱夹层的荷载传递和岩体变形特征；Peng等[16]结合现场监测数据，利用围岩位移场的微缩模型判断围岩的稳定性；Song等[17]通过数值模拟分析验证了上述方法的合理性和可行性；Qi等[18]基于实证、分析和数值方法，开发了软弱围岩支座设计系统的软弱围岩支护设计方法，用于软弱围岩支护需求估算和设计支护系统。郝婷等[19]依托马家寨隧道工程通过有限元软件MIDAS GTS NX建立有无超前支护的隧道出口端模型，分析总结了富水软岩卸荷软化和水软化的机理和工程特点。Ding等[20]考虑浸水时间的影响，提出了开挖卸荷弱化条件下岩石损伤本构模型，并将该模型应用于新建立的有限元模拟方法。目前，国内外学者虽然对富水软岩隧道的受力特性进行了广泛的研究并取得了较多的成果，但是对于高地应力富水炭质板岩类围岩方面研究不多，尤其是对于炭质板岩与其他岩体的软硬互层围岩研究甚少，因此有必要进一步研究。

渭武高速木寨岭公路隧道穿越炭质板岩破碎带，且破碎带处于高地应力地层段，隧道围岩遇水即融，地质极为脆弱。在隧道施工过程中，同时出现了喷射混凝土结构开裂掉块、钢架扭曲等现象，导致反复拆换拱架，工程进度停滞不前，因此，木寨岭公路隧道成为整个渭武高速公路的控制性工程。本文以木寨岭公路隧道为实际工程背景运用有限差分法软件FLAC3D分别建立了不同含水率下双侧壁导坑法和三台阶七步开挖法的数值模拟模型；分析讨论了两种施工方法下，围岩压力、竖向和水平位移、塑性区随着围岩含水率增加的分布规律和发展情况，研究成果可为不同含水率下的高地应力区炭质板岩段的支护、衬砌的设计及施工提供参考。

2 工程概况

木寨岭公路隧道位于甘肃省漳县、岷县交界地带，设计时速为80 km/h，左洞长15 226 m，右洞长15 168 m，隧道最大埋深为629.1 m，距2016年全线贯通的兰渝铁路木寨岭隧道约1 km。

隧道围岩以富水软弱炭质板岩为主，隧道受构造应力影响十分显著，深埋条件下的高地应力围岩大变形问题显著。隧道选址地海拔2 500～3 100 m不等，地势较高，地形起伏变化大，山体较为陡峭，且山沟、山谷多呈现“V”字型深切，因此其山体坡度较高，多大于50°。隧址地山脊段多呈现裸露岩石，且受气候影响裸露岩体出现较严重的风化现象，节理裂隙发育。根据勘察设计资料，隧道影响范围内共发育有11条断层，且受板块构造挤压作用围岩以断层压碎岩为主，岩体节理裂隙极为发育且具有一定程度的连通性，其断层破碎带如图1所示。受断层现象的影响，断层附近岩体多呈现碎裂结构和松散结构，岩体破碎，节理发育，给地下水的渗流提供了通道，因此隧道选址区地下储水量和施工涌水量较大，严重影响隧道的稳定性。渭武高速木寨岭公路隧道支护结构设计如图2所示。

图1 木寨岭公路隧道围岩状况

3 模型建立

3.1 模型尺寸和边界条件的确定

本文是以渭武高速木寨岭公路隧道工程为依托，故模型尺寸采用该隧道的设计尺寸。根据参考资料，数值模型水平方向的长度可取为隧洞跨径的3～8倍，同时对于深埋高地应力隧道，垂直方向上的长度同样可取为3～8倍隧洞跨径[21]。因此，本文数值模型沿开挖方向(模型中的Y方向)取100 m，垂直方向(模型中的Z方向)取80 m，水平方向(模型中的X方向)取100 m。为了减少单元的数量，隧道开挖界限内部单元边长以0.5 m为基准，隧道附近岩土体单元边长以1.0 m为基准，距离隧道较远的岩土体单元边长以3.0 m为基准，作用在岩层上部的重力作用等效于同样效果的均布荷载作用。选用限制位移法固定边界，对水平和前后方向边界设置位移约束，对垂直方向只在下边界设置位移约束而上边界不设置约束。另外，在数值模型的上边界设置相当于590 m埋深的均布荷载(11.8 MPa)。建立的数值模型如图3所示。

3.2 围岩及软硬互层下的力学参数的确定

本文数值模拟的岩层为炭质板岩与砂质板岩软硬互层，且具有一定的倾角(60°)，不仅需要考虑炭质板岩和砂质板岩的力学参数，还需给出软硬互层结构面的力学参数。砂质板岩作为硬岩，遇水软化作用不显著，故力学参数根据现场勘察设计资料结合有关规范确定；对炭质板岩需要考虑不同含水率下不同的岩样参数，故采用参考文献[10]中所进行的炭质板岩浸水试验中的参数，即分别取用泡水0、5、15、25 d下的参数；炭质板岩与砂质板岩之间结构面的参数，根据参考文献结合勘察设计资料确定。假定炭质板岩和砂质板岩遵循理想弹塑性本构关系和摩尔库伦屈服准则。岩土体的各项力学参数列于表1、2。

3.3 支护结构采取的计算假定和参数选取

对于数值模拟中的支护结构，喷射混凝土采用壳单元(shell单元)进行模拟，中空注浆锚杆采用锚索单元(cable单元)进行模拟，二次衬砌采用实体单元进行模拟。其中喷射混凝土厚度为25 cm，中空注浆锚杆直径为80 mm，二次衬砌厚度为50 cm，超前注浆小导管长9 m、倾角为10°，同时考虑到高压浆液注入后产生的扩散作用，设定浆液加固圈厚度为0.8 m。具体参数如表3所示。

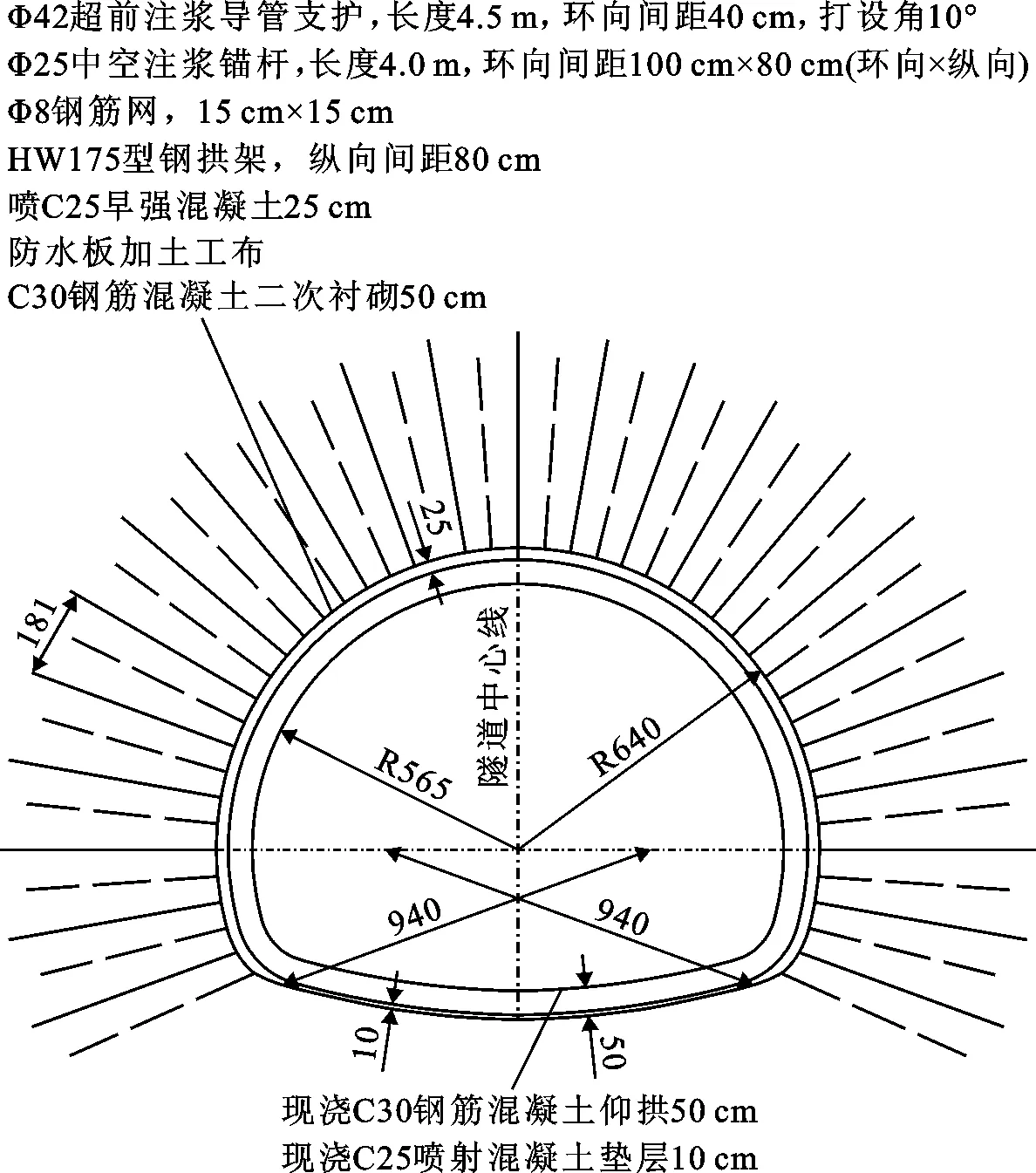
图2 木寨岭公路隧道支护设计图(单位：cm)

图3 建立的数值模型示意图

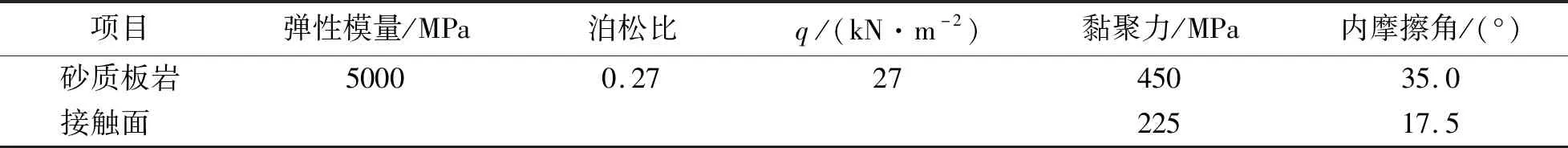
表1 木寨岭公路隧道岩土体力学参数

表2 木寨岭公路隧道不同含水率下的炭质板岩力学参数

3.4 监测点设置方案

由于在数值模拟中，建立模型所设置的边界范围有限，边界范围的约束会对数值模拟的监测结果产生较大的不利影响，故应在隧道开挖进洞一段距离后设置监测点进行监测。根据弹性力学圣维南原理，为减少开挖扰动和边界效应带来的监测误差，各监测点设置在距离隧道开挖掌子面16 m处，即Y=16 m处。

当采用三台阶七步开挖法进行数值分析时，分别在拱顶、上台阶左拱腰、上台阶右拱腰、上台阶左拱脚、上台阶右拱脚、中台阶左拱脚、中台阶右拱脚、仰拱中央共设置10个监测点(1#～10#监测点)。当采用双侧壁导坑法进行数值分析时，分别在拱顶、左边墙、右边墙、左拱腰、右拱腰、仰拱中央共设置6个监测点(1#～6#监测点)，两种开挖方法的监测点位置见图4。

表3 木寨岭公路隧道支护结构力学参数表

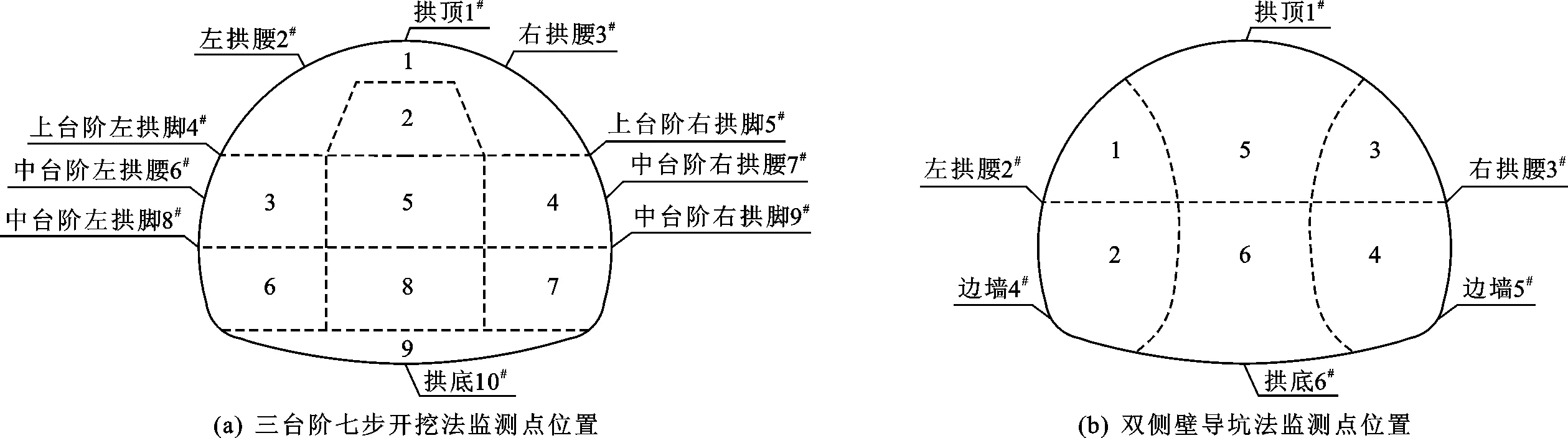
图4 隧道两种开挖方法的监测点位置示意图

4 结果与分析

为了简化计算，本文在进行数值模拟时不考虑爆破振动的响应，数值模型中隧道开挖长度为80 m，共平均分为50步，每步1.6 m。通过绘制隧道断面图，网格划分等FLAC3D规范操作顺序得到三台阶七步开挖和双侧壁导坑施工法的数值模型和支护结构图。三台阶七步开挖法和双侧壁导坑法的施工顺序数值模型如图5所示。

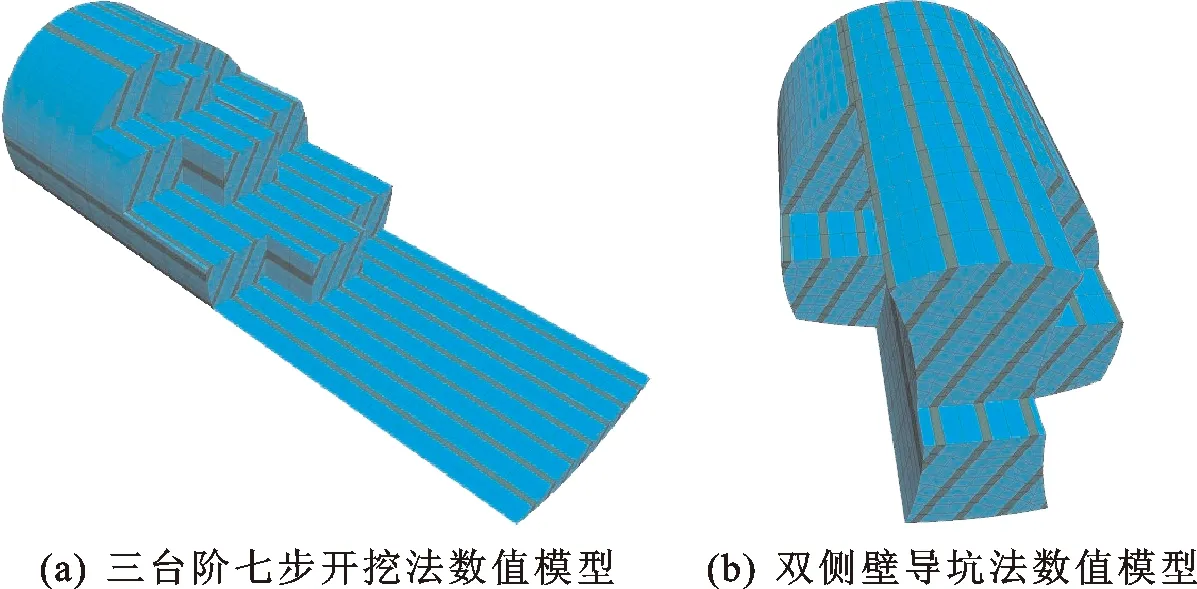
图5 隧道两种开挖方法的施工顺序数值模型示意图

通过数值模拟，得到了高地应力炭质板岩隧道在不同含水率下，三台阶七步开挖法和双侧壁导坑法不同的施工阶段对隧道围岩稳定性影响的计算结果，包括围岩位移、围岩应力、塑性区、支护结构受力等。

4.1 围岩位移场分析

图6、7给出了围岩不同泡水时间下隧道两种开挖方法的最大水平收敛和沉降变化曲线。从图6、7中可以看出，随着含水率的不断增大，围岩开挖后产生的水平收敛逐渐增大，三台阶七步开挖法开挖下，干燥未泡水时其水平收敛11.97 cm，泡水25 d后其水平收敛为58.30 cm；双侧壁导坑法开挖下，干燥未泡水时其水平收敛仅有4.16 cm，泡水25 d后其水平收敛达到15.70 cm。随着泡水时间的不断增大，围岩开挖后产生的沉降也越来越大，以拱顶沉降为例，三台阶七步开挖法开挖下，干燥未泡水时其拱顶沉降为17.78 cm，而泡水25 d后达到69.40 cm；双侧壁导坑法开挖下，干燥未泡水时其拱顶沉降为16.10 cm，而泡水25 d后达到30.10 cm。结果表明，隧道围岩含水率越高，其围岩强度越小，围岩的水平收敛和竖向位移越大。根据相关实测资料[22]，木寨岭公路隧道F2断层破碎带处拱顶沉降和水平收敛均在数十厘米以上。在K0918处，换拱前拱顶沉降高达120 cm，水平收敛也高达108 cm，换拱后，围岩变形得以控制在30 cm以内。以上实测资料可证明本数值模拟的准确性，并验证三台阶七步开挖法和双侧壁导坑法对控制围岩变形有良好的效果。

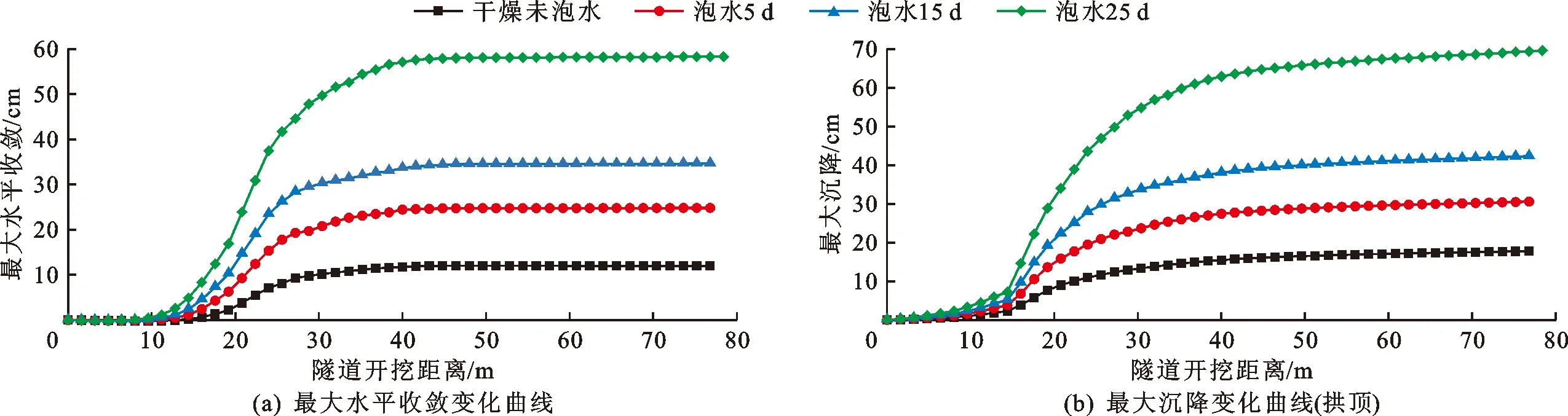
图6 围岩不同泡水时间下三台阶七步开挖法施工隧道最大水平收敛和沉降变化曲线

图7 围岩不同泡水时间下双侧壁导坑法施工隧道最大水平收敛和沉降变化曲线

4.2 围岩应力场分析

图8、9给出了围岩不同泡水时间下隧道两种开挖方法的最大应力云图。由图8、9中应力云图的变化可知，在不同的泡水时间下，随着开挖距离的增大，围岩最大应力有如下规律：(1)采用这两种开挖方法进行隧道开挖，围岩的最大应力均发生在隧道的左、右边墙处。当含水率为1.24%时(泡水25 d)，随着开挖距离的不断增加，在仰拱处也出现了较大应力。木寨岭公路隧道炭质板岩段实际施工中所出现的变形破坏类型有边墙挤压内鼓、钢拱架扭曲、隧底隆起、局部塌方等[23]，与本文数值模拟所得围岩应力场规律相符；(2)在相同含水率条件下，随着开挖的进行，两种开挖方法下的围岩最大应力都在不断增加，说明在隧道开挖过程中，该炭质板岩段围岩受扰动程度不断增大；(3)随着含水率的增加，隧道周边的最大应力都在不断减小，且最大应力出现在边墙处；(4)相比三台阶七步开挖法，采用双侧壁导坑法施工时其最大应力更大。

4.3 围岩塑性区分析

塑性区在一定程度上代表了围岩受扰动程度的大小，研究塑性区变化有助于分析含水率对炭质板岩隧道稳定性的影响。图10、11给出了围岩不同泡水时间下隧道两种开挖方法的塑性区云图。由图10、11可知：(1)由于隧道设计结构和炭质板岩、砂质板岩受具有一定倾角的软硬互层所带来的偏压影响，因而截面的塑性区形状并非呈现标准的圆形，塑性区仅在沿层理面方向和垂直于层理面方向分布较为广泛；(2)随着炭质板岩含水率的不断增大，围岩吸水软化程度加深，强度不断减弱，进而使由隧道开挖引起的塑性区范围不断增大；(3)随着炭质板岩含水率的不断增大，塑性区在除了层理面法向和切向的分布趋于广泛，即随着含水率的增加塑性区分布受具有一定倾角的软硬互层围岩的影响逐渐减小；(4)与三台阶七步开挖法相比，双侧壁导坑法施工下的塑性区分布受软硬互层影响更小，说明导坑内的支护对偏压效应有一定的抑制作用。

5 隧道施工方法比较

对于高地应力富水炭质板岩段，施工方法的选择对围岩的稳定性极为重要，甚至会影响施工人员的生命安全。因此，基于上述数值模拟计算的结果，对比三台阶七步开挖法施工和双侧壁导坑法施工的隧道围岩沉降、围岩水平收敛、围岩最大应力、塑性区范围，可以初步评价该两种开挖方法下围岩的稳定性，为施工方法的选择提供参考。

三台阶七步开挖法和双侧壁导坑法施工隧道在不同开挖距离下的最大沉降、仰拱回弹、水平收敛的对比如图12所示。由图12中可以得出，采用双侧壁导坑法施工时，隧道的最大沉降、仰拱回弹、水平收敛均小于三台阶七步开挖施工法。因此从控制变形的角度来看，双侧壁导坑法施工更为安全。

对比表4、5中的受力参数值可知：采用双侧壁导坑法施工时，隧道周边围岩的最大应力略大于三台阶七步开挖法，说明采用双侧壁导坑法施工时对围岩的支护作用较强，而对其应力释放不足。但由于双侧壁导坑法施工开挖闭合成环所需时间较长、防水层施作较晚且防水层整体性较差(因为钢架无法顺序连接导致初期支护连接不够紧密)，故在富水隧道中防水性较差，在实际工程中常采用两种施工方法交替使用。