地震动和结构参数双重随机的重力坝抗滑稳定可靠度分析

2022-10-26李世强宋志强姚倩茹刘云贺

水资源与水工程学报 2022年5期

李世强,宋志强,姚倩茹,刘琛,刘云贺

(1.西安理工大学省部共建西北旱区生态水利国家重点实验室,陕西西安 710048；2.中铁第一勘察设计院集团有限公司，陕西西安 710043)

1 研究背景

混凝土重力坝的失稳破坏多是沿建基面或复杂地基的深层滑移面发生滑动，地震作用下的重力坝抗滑稳定是大坝安全控制的重要因素之一，因此，重力坝动力抗滑稳定可靠度分析研究具有重要的理论意义和工程应用价值。

目前，关于重力坝抗滑稳定可靠度的研究大多集中在静力荷载和复杂地基工况[1-4]以及可靠度算法优化[5-7]等方面，针对地震作用下考虑结构参数随机的重力坝抗滑稳定可靠度研究并不多见。孙平等[8]结合极限分析方法，提出了一种静力工况下更加合理的考虑岩体抗剪强度各向异性特征的重力坝抗滑稳定分析方法。黄灵芝等[9]采用传统的刚体极限平衡法和JC法，考虑滑动面抗剪断摩擦系数和黏聚力系数的随机性，分析了某重力坝的抗滑稳定可靠度。朱晓斌等[10]提出一种基于猫群算法的加权动态响应面可靠度分析方法，克服了蒙特卡洛法需要大量计算的缺点，在保证较高的准确度前提下，有效地提高了结构可靠度的计算效率。甘珩佚等[11]在考虑材料敏感性的基础上，运用动态位移反分析技术和响应面法建立了重力坝抗滑稳定极限状态方程，结合大坝实时变形监测数据，提出了重力坝抗滑稳定可靠度动态评估模型，实现了复杂运行条件和多种随机参数下重力坝抗滑稳定安全的动态定量评估。何蕴龙等[12]基于首次超越破坏理论，在JC法和泊松过程法基础上，将随机变量转换成随机过程进行计算，研究了重力坝同时受随机动力荷载和随机静力荷载情况下的抗滑稳定。陈颖等[13]基于首次超越破坏理论，提出了同时考虑结构参数和动荷载随机性的动力可靠度分析方法。

在我国西南强震区建有很多重力坝工程，对这些重力坝的抗滑稳定可靠度进行分析时，有必要考虑地震动力作用。同时由于实际施工过程中材料分布的不均匀，结构参数的随机性也是必须考虑的因素。然而，目前考虑地震荷载和结构参数双重随机的重力坝抗滑稳定可靠度分析研究进展缓慢，难点在于考虑结构参数随机的可靠度分析是以随机变量为基础，而地震动输入的动力可靠度分析是以随机振动理论为基础，二者很难进行耦合求解。

本文建立了考虑地震动和结构参数双重随机性的重力坝建基面抗滑稳定极限状态方程，将随机地震动输入产生的坝体水平和竖向惯性力随机过程的最大值作为随机变量，尝试根据随机过程参数获得此随机变量的均值和方差，进而将地震荷载和结构参数双重随机性问题统一到随机变量模式下，采用JC法获得重力坝建基面抗滑稳定可靠度，并进一步考虑地震发生的概率，分析了重力坝抗滑稳定的失效概率，最后分析了各结构随机参数对可靠度和失效概率的敏感性。

2 重力坝抗滑稳定极限状态方程

静力工况下，结构可靠度分析常用的功能函数为：

Z=L-Y

(1)

式中：L为安全界限值；Y为结构响应值；结构功能函数Z>0的概率即为结构可靠度。

将上述功能函数运用到结构动力计算中，输入随机地震动，结构的响应值是不断变化的，因此结构功能函数也是变化的，称为功能随机过程[14]：

Z=L-Y(t)

(2)

假定地震动为高斯平稳随机过程，则考虑结构参数随机后的重力坝建基面抗滑稳定极限状态方程可写为：

(3)

式中：Z=g(X1,X2,…,Xn)为不考虑地震动作用时的抗滑稳定极限状态方程；X1,X2,…,Xn为反映结构参数变化的随机变量；FH(t)、FV(t)分别为坝体在高斯平稳随机地震动作用下的水平和竖向地震惯性力，均为高斯平稳随机过程且均值均为0；f′为坝基滑动面抗剪断摩擦系数。当Z>0时结构安全，Z<0时结构失效。

上述极限状态方程中既含有结构参数随机变量，也含有地震动水平和竖向惯性力随机过程，无法直接进行可靠度的求解。文献[12]采取将随机变量转换为随机过程的思路，先采用JC法求解g(X1,X2,…,Xn)=0的可靠度，然后用均值和可靠度指标将其表示为随机过程，再将多个随机过程转换为一个已知均值和方差的总随机过程，进而按照首次超越破坏准则，采用Coleman给出的结构动力可靠概率的计算公式进行可靠度求解。

该方法中的g(X1,X2,…,Xn)=0的随机变量与静力荷载有关，与地震动惯性力随机过程无关，且该研究中的结构参数是确定性常量。当考虑结构参数为随机变量时，即g(X1,X2,…,Xn)=0的随机变量为与结构参数有关的随机变量，其中的密度、弹性模量、泊松比等随机变量均会对地震动惯性力随机过程产生影响，即结构参数随机变量与地震动惯性力随机过程相关，因此文献[12]中的方法不一定适用。

3 基于地震动和结构参数双重随机的动力可靠度分析方法

本文尝试采用将随机过程转换为随机变量的思路求解上述极限状态方程的可靠度。由于按方程式(3)求出的结构可靠度是随着时间发生变化的，将方程式(3)中的随机过程进行功能极小值变换，即：

(t∈[0,T]

(4)

式中：FH max(t)和FV max(t)分别为随机过程FH(t)和FV(t)在时间区域[0,T]内的极大值。

依据结构动力分析可靠度常采用的首次超越破坏准则，即结构极限状态函数首次出现小于零的情况，则认为抗滑稳定失效。此时，按方程式(4)求出的可靠度是结构在时间区域[0,T]内的最小可靠概率，即为[0,T]内的抗滑稳定可靠度。根据随机振动原理，对于线性结构可以将随机过程FH(t)和FV(t)的最大值FH max(t)和FV max(t)表示为随机变量，其均值和方差可以用随机过程参数求得：

maxFH(t)=pHσFH

(5)

maxFV(t)=pVσFV

(6)

式中：σFH和σFV分别随机过程FH(t)和FV(t)的标准差(均值为0时的均方根值)，N；pH和pV为随机变量。

公式(5)、(6)中两个随机变量pH和pV的均值(μ)和方差(σ)可根据Davenport公式[15]求得：

(7)

(8)

(9)

(10)

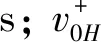
将公式(5)、(6)代入公式(4)，得到重力坝抗滑稳定极限状态方程为：

(11)

式中：σFH和σFV为随结构参数(弹性模量、泊松比、密度等)变化的随机变量。

采用不含交叉项的二次多项式对随机变量σFV和σFH进行拟合[17]。假设有n个随机变量，结构在输入地震动和结构参数双重随机下的响应均方根值可以表示为：

σFV=fV(x1,x2,…,xn)

(12)

σFH=fH(x1,x2,…,xn)

(13)

式中：aV、aH、bVi、bHi、cVi、cHi均为待定系数。共有4n+2个系数，需要4n+2个样本点对系数值进行计算。样本点的选取应尽量在(μx-fσx,μx+fσx)内选取，f的取值一般在1～3之间。有限元模型取样本点的参数进行随机地震动分析得到对应的响应值，即可求得待定系数。

将公式(12)、(13)代入方程式(11)，则抗滑稳定极限状态方程转化为：

(14)

最终，重力坝沿建基面的动力抗滑稳定极限状态方程转化为由结构参数随机变量组成的显式函数，可直接采用JC法进行随机地震动作用下抗滑稳定可靠度的求解。

4 考虑双重随机性的重力抗滑稳定可靠度分析算例

4.1 计算模型

本文以弄另水电站[18]非溢流坝7#坝段的较危险断面坝0+247.00 m为例进行分析，算例重力坝坝体和地基有限元模型如图1所示。坝体上、下游水位分别为962.00、941.00 m；该坝段建基面高程为936.50 m，坝顶高程为964.50 m，坝顶宽度为8.00 m。库水对大坝的作用通过附加质量矩阵计算[19]，防渗帷幕处的渗透压力折减系数取0.35，工程坝址处的设计地震烈度为Ⅷ度，设计平坦基岩地表水平加速度峰值为0.2g。

4.2 结构参数随机分布

结构可靠度计算时，随机参数的选择对坝体结构抗滑稳定有较大影响。本文选择坝体与基岩滑动面的抗剪断摩擦系数f′、抗剪断黏聚力系数c′、坝体密度ρ、坝体的弹性模量E1、坝体泊松比μ1、地基的弹性模量E2、地基泊松比μ2共7个随机参数，各参数的均值、变异系数及分布状态统计如表1所示。

图1 算例重力坝坝体-地基有限元模型

表1 坝体与基岩结构参数随机变量统计

考虑以上随机变量，重力坝沿建基面的抗滑稳定极限状态方程为：

Z(x1,x2,x3,x4,x5,x6,x7)=g(x1,x2，x3)-pHσFH-

(15)

其中：

g(x1,x2,x3)=f′ (G-U)+c′A-P

=x1(x3Vg-U)+x2A-P

(16)

式中：G为坝体自重，N；U为建基面上的扬压力，N；V为坝体单宽体积，m3；g为重力加速度，m/s2；A为坝体建基面单宽面积，m2；P为作用在坝体上的水平合力，N。

4.3 地震动的随机

工程场地设计地震烈度为Ⅷ度，平坦基岩地表水平加速度峰值为0.2g。假定地震动加速度时程是均值为0的高斯平稳随机过程，地震动加速度输入采用金井清过滤白噪声模型[20]：

(17)

式中：特征频率ωg=5.2π rad/s，特征阻尼比ξg=0.60。

地面加速度过程的功率谱密度函数为：

S(ω)= │H(ω)│2S0

(18)

式中：S0为功率谱强度，计算得水平向地震动加速度谱强度SgH=0.0133 m2/s3，竖直向地震动加速度谱强度SgV=0.0059 m2/s3。

计算出的地震动加速度水平向和竖直向功率谱密度(SH、SV)随频率(f)的变化曲线见图2。

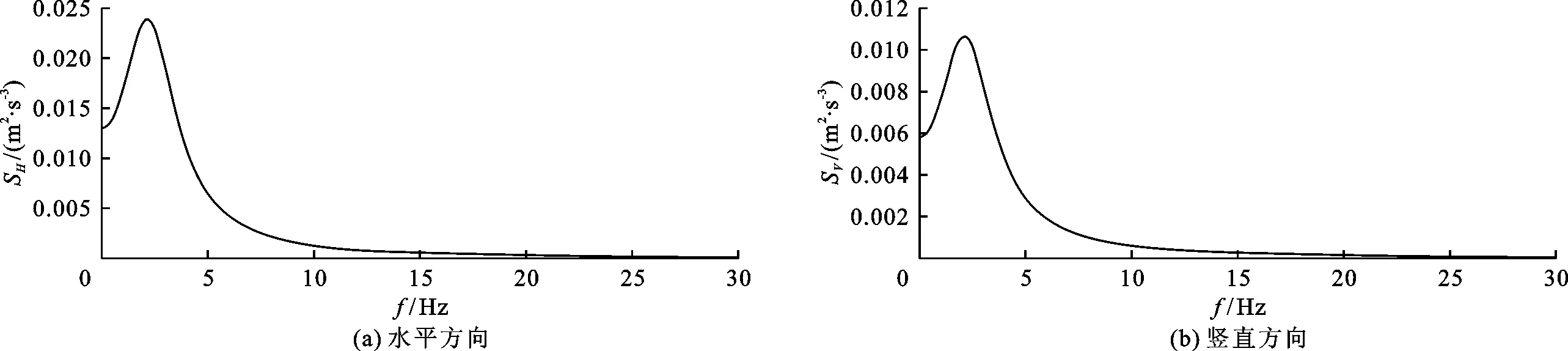
图2 水平向和竖直向的地震动加速度功率谱密度随频率变化曲线

4.4 计算结果及分析

通过不含交叉项二次多项式对均方根响应值进行拟合时，选择坝体的密度ρ、弹性模量E1、泊松比μ1以及地基的弹性模量E2、泊松比μ2作为参数随机变量，对模型参数赋值进行有限元计算，得出一系列地震响应结果，代入公式(12)、(13)求解待定系数。采用编制的JC法计算程序计算可靠度，其失效概率pf通过公式pf=Φ(-β)计算，其中Φ为标准正态分布函数。计算得到该混凝土重力坝沿建基面抗滑稳定可靠指标为β=4.23，失效概率pf=0.001 17%。

在计算重力坝地震失效概率时，由于地震动具有随机发生的特性，同时也应计算坝址场地地震发生的概率。未来t年内发生I度地震的概率分布函数可近似地表示为[21]：

(19)

式中：ω为地震烈度，其上限值为12；ε为众值烈度；I为坝址处地震烈度；K为形状参数。

坝址处相应的地震烈度的发生概率P(I)用下式表示：

P(I)=Ft(I+1)-Ft(I)=1-Ft(I)

(20)

计算得出Ⅷ度地震烈度的发生概率P(I)为12.09%。最终考虑该烈度大小的地震发生概率后的混凝土重力坝抗滑稳定失效概率Pf可以通过下式计算：

Pf=P(I)·pf

(21)

在水利工程中，结构的承载能力标准通过结构允许可靠指标进行控制，结构的允许可靠指标是以年计失效概率计算推导的。假设结构设计基准年Nd与结构的使用年限T相同，即Nd=T，则结构的年计失效概率Py为：

(22)

根据规范《水利水电工程结构可靠性设计统一标准》(GB 50199—2013)[22]规定，1级主要建筑物的设计寿命为100 a，则该坝设计基准期内的年计失效概率Py计算结果如表2所示。

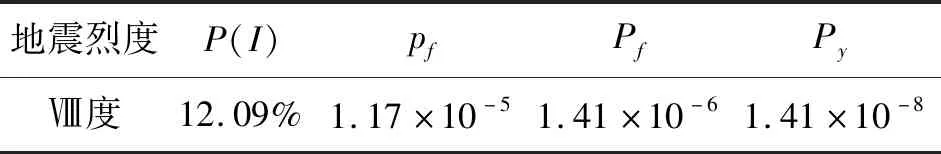
表2 混凝土重力坝地震抗滑稳定失效概率

重力坝抗滑稳定的可靠性应以可靠指标表示，在考虑地震发生概率的基础上以年计失效概率计算重力坝建基面的抗滑稳定可靠度指标，根据公式β=Φ-1(1-Py)进行计算。规范[22]中规定，结构可靠度应不小于目标可靠指标，本工程实例计算得到的重力坝建基面抗滑稳定可靠度指标β=5.55，满足规范中对水工建筑物设计安全的要求。

4.5 结构参数随机对可靠度影响分析

为了解结构参数随机对重力坝抗滑稳定可靠度的影响，同时开展了结构参数为常量(除f′、c′外)情况下的可靠度计算，常量的具体数值取为原随机分布的均值，并与结构参数随机情况下的可靠度分析结果进行对比，如表3所示。由表3可见，坝体参数随机使得重力坝抗滑稳定可靠度指标降低，失效概率和年计失效概率增大；坝体参数确定的工况下结构可靠度指标β=5.20，其结果偏大，会造成失效概率的较大低估。

表3 重力坝抗滑稳定可靠度计算对比分析结果

为进一步了解各单一结构参数变化对可靠度的影响程度，采用正交试验法，开展了各随机变量对可靠度的敏感性分析，将f′、c′、ρ、E1、μ1、E2、μ2这7个参数均作为影响因素，不考虑各参数之间的交互作用。分别取各参数均值的±5%、±15%作为4个试验水平[23]。根据正交试验结果，采用极差法获得各随机变量敏感性。各随机变量对可靠度的敏感性程度Rj如图3所示。由图3可知，对重力坝沿建基面的抗滑稳定可靠度最为敏感的结构参数为坝体密度ρ，其次是地基泊松比μ2，滑动面的抗剪断黏聚力系数c′和抗剪断摩擦系数f′较为敏感，其他参数影响相对较弱。

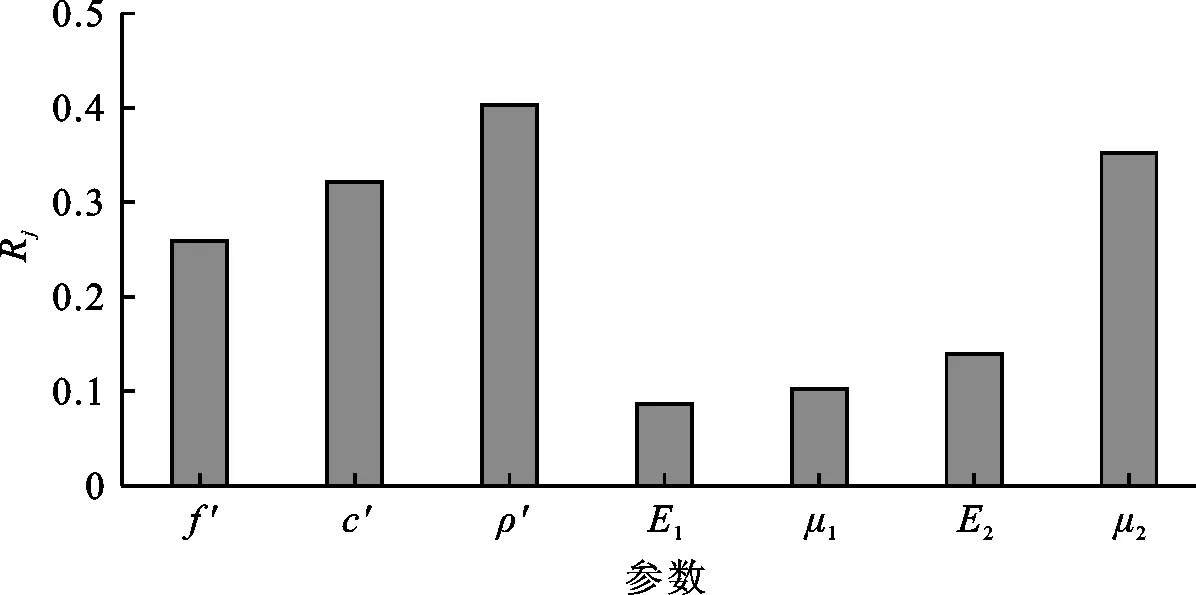
图3 各参数对重力坝抗滑稳定可靠度敏感性分析结果

5 讨论

本文对比计算了考虑地震发生概率的地震参数和结构参数双重随机以及不考虑结构参数随机下重力坝建基面抗滑稳定可靠度，计算结果显示参数双重随机下的可靠度指标β=5.55，不考虑结构参数随机的可靠度指标β=6.33，考虑参数双重随机的重力坝抗滑稳定可靠概率降低，失效概率增大。造成这种现象主要是因为考虑的随机参数越多，越接近实际情况，其抗滑稳定可靠度越接近真实可靠度。通过正交试验法对结构随机参数进行可靠度敏感性分析的计算结果显示，坝体密度对结构可靠度最为敏感，极差值为0.403，其次为地基泊松比、滑动面的抗剪断黏聚力系数和抗剪断摩擦系数，极差值分别为0.351、0.321和0.259，这与相关的研究结果[24]规律相同。造成这种现象的主要原因是由于坝体密度的变异系数略大，以及坝体密度与静力和动力计算过程均有关，故其对综合可靠度的影响最大。在地震频发区，应更关注结构的动力可靠度，进行动力可靠度分析时考虑地震参数和结构参数的随机性更加符合实际。本文在考虑地震参数的随机时采用了高斯平稳地震动输入模型，后续将采用非平稳地震动模型来模拟地震动随机性，构建更加符合实际的结构动力可靠度分析方法。