基于多目标不确定性机会约束规划的矿区水资源配置研究

张 真，张光明,2，张盼月

(1.中国人民大学 环境学院，北京 100872；2.河北工业大学 能源与环境工程学院，天津 300401；3.北京林业大学 环境科学与工程学院，北京 100083)

1 研究背景

我国西北干旱地区分布着丰富的矿产资源，“十二五”期间，我国建设的14个大型煤炭基地中有11个位于干旱地区[1]。水资源缺亏和采煤带来的生态破坏双重制约着干旱地区“绿色矿山”理念的实践。如矿坑排水加剧了区域水资源的短缺[2]、采煤塌陷区的生态恢复和景观重建增大了用水缺口[3]等问题，矿区生态恢复与水资源补给之间的矛盾日益突出[4]。矿区水资源不足严重影响着生态环境和经济社会的发展，科学分配及合理利用矿区有限的水资源，提高水资源综合利用效率，是减轻矿区缺水所造成的负面影响的方案之一，对保障矿区可持续发展以及生态健康具有重大意义。目前，已有研究提出了矿区水资源优化配置的多目标规划模型，并证明科学分配水资源可以缓解矿区水资源供需矛盾[5-6]。

水资源优化配置(water resources optimal allocation，WROA)的研究始于20世纪50年代，一系列数学方法[7]已被应用于研究之中，例如线性规划、动态规划、目标规划和多目标规划[8]等。随着矿区生态恢复需求的上升，基于生态优先的多目标配置模型逐渐被重视[9]，这类模型中所讨论的生态效益目标关注点为重点污染物COD或氨氮的排放量[10-11]。然而，矿产资源开发损毁了土壤结构，导致矿区碳固存能力下降甚至丧失[12]。通过加大矿区生态恢复用水，可以从植被光合作用及土壤碳汇两方面促进碳减排[13]，从而带来不容忽视的生态效益。因此，本文构建基于碳排放量的生态效益目标，并与传统的以污染物排放量为目标的模型进行对比。

在水资源配置过程中，由于矿井水产量存在波动，因而供水效益、成本效益和用户需水量等参数具有不确定性，难以精确获取。为解决上述问题，不确定性优化技术已逐渐应用于水资源优化配置中[14]。已有学者提出了不确定性模糊机会约束规划(inexact fuzzy chance-constrained programming，IFCCP)的理论框架[15]，当多参数不确定性和随机干扰同时存在时，建立了带有区间数和模糊数的扩展MSP(multistage stochastic programming)模型[16]。目前，不确定性模型已在城市水系统分配、灌区农业水系统管理[17]等方面得到了很好的应用。因煤矿开采和矿井排水严重影响煤矿区的水资源供给，所以煤矿区水资源利用及管理与城市、灌区等其他场景相比进一步增加了资源配置过程的不确定性。考虑到矿区水资源配置过程中不确定性因素的影响，为获取最优方案，结果可能不满足约束条件。而机会约束规划通过建立约束的可能性不小于某些置信水平，可应用于矿区水资源配置方案的决策中。

在水资源配置模型的求解中，其求解方法按照原理的不同分为传统数学算法和智能优化算法两大类。常见的传统算法有加权法、约束法和线性规划法[18-19]等，此类算法本质上是将多目标函数通过数学运算转化为单目标函数，再对单目标函数进行优化求解获取多目标函数的最优方案。传统算法受到初始值和主观因素的双重影响[20]，容易出现局部最优而忽视全局最优的情况。智能优化算法包括遗传算法、粒子群算法等。以遗传算法为代表的智能优化算法具有可生成多个点并进行多方向搜索的特征，非常适合求解搜索空间非常复杂的多目标优化问题[21]。因此，本文构建了适用于矿区水资源配置的不确定性机会约束规划多目标模型(multi-objective uncertain chance-constrained programming-genetic algorithm,MUCC-GA)，利用第二代非支配排序遗传算法(elitist non-dominated sorting genetic algorithm,NSGA-Ⅱ)求解该模型。

2 不确定模型的一般形式

不确定性机会约束规划(uncertain chance-constrained programming，UCC)是一种将不确定理论和机会约束规划相结合的优化方法。该规划方法通过使用区间数的方式有效地解决了实际情况中的不确定环境，另外在模型中还通过设定置信度的方式放宽了约束条件的限制，即根据实际情况和决策者对风险的承受能力，遵守约束的可能性高于预定的置信度即可。UCC的一般形式如下：

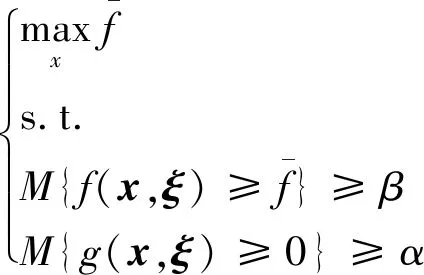
(1)

作为单目标的扩展，多目标形式机会约束规划(MUCC)的构造如下：

(2)

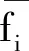
3 基于遗传算法的多目标不确定性机会约束规划模型(MUCC-GA)

矿区的供水系统包括地表水、地下水、矿井水和再生水，用水系统包括工业用水、生活用水和生态用水。从多水源到多用户的供水系统简化结构如图1所示。供水系统优化的目的是通过机会约束规划模型选择最佳配水方案，即水源i向用户j的供水量xij值(i=1，2，…，I；j=1，2，…，J)，MUCC-GA模型的多目标决策变量如表1所示。

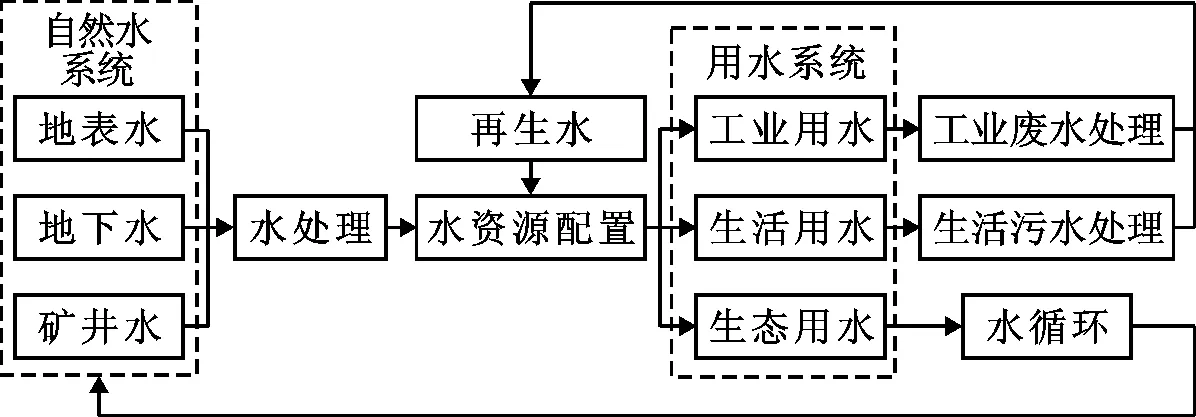
图1 矿区多水源到多用户的供水系统结构简图

3.1 目标函数

不确定性多目标模型将矿区内生活、生产、生态需水部门的配水量作为决策变量，兼顾经济发展和生态恢复目标，建立矿区水资源不确定性模糊机会多目标优化模型。其中，除有确定性参数的碳净排放目标外，其他目标均因含有不确定性因素而写为机会约束规划形式。

表1 MUCC-GA模型的多目标决策变量

(1)生态效益目标。在识别碳“源”与碳“汇”的基础上，建立碳净排放目标函数，其中包括生活用水产生的碳排放量、工业供水过程产生的碳排放量、再生水回用减少的碳排放量和生态系统用水带来的碳吸收量，其表达式如下：

(3)

式中：xij为从i水源向j用水部门的供水量，m3；Tij为碳排放系数，kg/m3，碳排放过程其值为正，碳吸收过程其值为负。

用于对比的传统生态效益目标是通过减少主要污染物(一般选用COD指标)的排放总量，实现生态目标的最大化，其目标函数表达式如下：

(4)

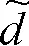
为了最大限度地最小化污染物排放总量，寻找目标函数f1在β1置信度下的最小值，将目标函数转换为机会约束规划形式：

(5)

(2)经济效益。经济效益为供水的净利润总额，即供水的收益和成本之间的总差额。净利润函数可以表示为：

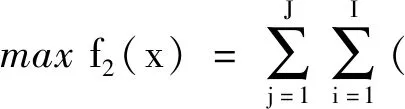
(6)

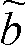
为最大限度地提高供水带来的经济效益，寻找目标函数f2在β2置信度下的最大值：

(7)

为了简化计算，目标函数应统一为求最小值的形式：

(8)

(3)社会效益。社会效益体现在提高矿区各个用水部门的需水满足度，降低水资源短缺带来的生活质量下降、生态恢复进度减缓等负面影响。因此，社会效益目标通过总缺水量最小化实现：

(9)

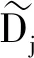
为了使总缺水量最小化，寻找目标函数f3在β3置信度下的最大值：

(10)

3.2 机会约束条件

约束条件是矿区水资源配置过程不能忽视的一部分，机会约束条件可以获得不同严格程度下的配水方案和最优目标。

(1)可供水量约束。水源供水量不得超过供应能力，即：

(11)

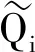
(2)需水量约束。水源供水量不得低于用户最低需水量，即：

(12)

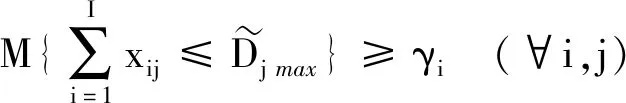
(13)

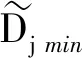
(3)非负约束

xij≥0 (∀i,j)

(14)

3.3 模型化简及求解

本文分别采用等价转换和加权最小偏差法的方法来求解不确定性机会约束多目标模型。

(1) 机会约束规划的等价转化

对于不确定模型，其求解应遵守以下定理[22]：

设g(x，ξ1，ξ2，…，ξn)为约束函数，其中ξ1，ξ2，…，ξn是独立的，且具有不确定性分布Φ1，Φ2，…，Φn。若g(x，ξ)随着ξ1，ξ2，…，ξt的增加而增加，随着ξt+1，ξt+2，…，ξn的增加而减小，则：

M{g(x,ξ)≤0}≥α

(15)

等价于：

g(x,φ1-1(α),…,φt-1(α),φt+1-1(1-α),…,

φn-1(1-α))≤0

(16)

因此，用于矿区水资源配置的MUCC-GA模型可等价转化为以下形式：

(17)

(2)基于遗传算法的模型求解方法。本文使用遗传算法(genetic algorithm，GA)对该多目标优化模型进行求解。遗传算法属于进化算法的一种，独立于最优化问题的经典算法之外。

在遗传算法中，对一定数量的候选解(个体)进行编码得到染色体，通过构建适应度函数对个体进行选择，筛选较弱的解，并对染色体进行突变产生下一代个体。重复若干代选择、突变后得到最优个体，这种算法的特点包括并行性高、鲁棒性强、容易达到全局最优等。标准遗传算法的流程如图2所示。在多目标优化中使用遗传算法，可以得到一组Pareto最优解，再根据实际情况及决策者偏好，从备选方案中选择。

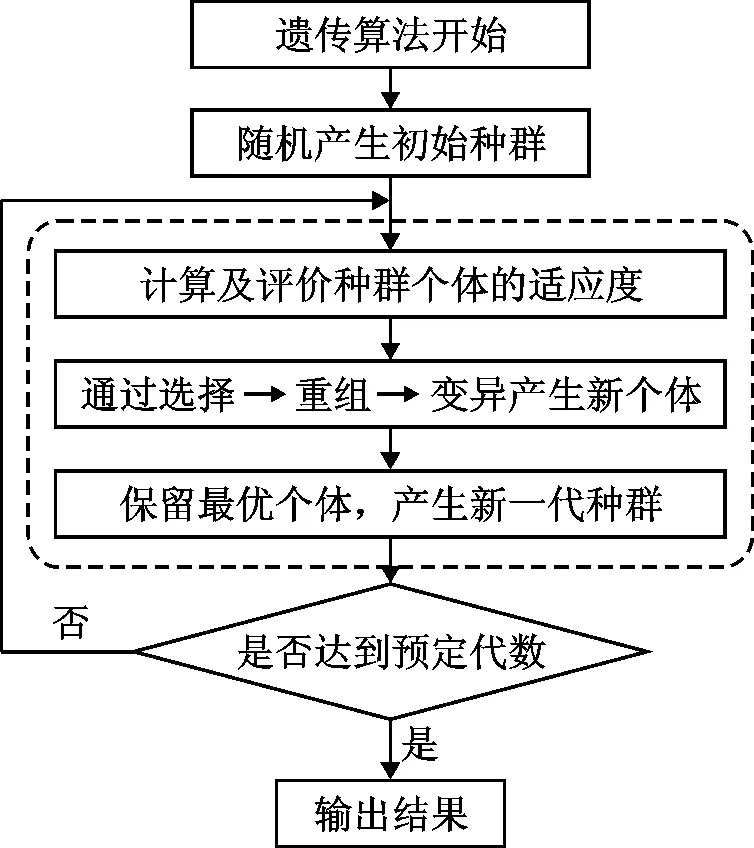
图2 标准遗传算法求解流程图

4 实例研究

羊场湾煤矿位于宁夏回族自治区灵武市宁东能源化工基地灵武矿区，是神华宁夏煤业集团有限责任公司所属的大型骨干企业之一。该煤矿隶属于被国务院确定为全国13个大型煤炭基地之一的宁东煤田。根据《羊场湾煤矿及选矿厂工程水资源论证报告》，宁东煤田基地处于温带干旱气候区，具有干燥、雨量少而集中、蒸发量大、日照时间长、冬春季风沙多、无霜期短等特点。矿区生态环境系统抗干扰能力弱，资源型缺水和水质型缺水问题并存。目前，羊场湾矿区企业正大力推进由资源消耗型向环境友好型发展，矿区整体供水结构和理念须进行改变，主要包括两个方面：(1)羊场湾煤矿目前所需的地下水资源由大泉水源地供给。然而，随着地下水被长期开采以及水资源的衰减，应大力节约地下水资源才能保障矿区的可持续发展；(2)矿井水作为非常规水资源，需要开辟其新的使用途径，从而解决矿区生态用水问题。基于生态理念的水资源多目标优化配置，应坚持“优先保障生活需水和生态环境用水、满足工业基本用水需求”的配置原则，实现可持续发展。

4.1 羊场湾矿区水量供需平衡分析

经过对矿区自然地理概况的调查研究表明，井田范围内可利用的地表水资源仅有西天河，该河流从井田东北角流过，径流空间分布具有总量少、年内分配不均、年际变化大的特点。矿区可供给水源包括当地地下水、外调地下水、外调地表水、矿井水和再生水。在资源供给方面，矿井水作为具有矿区特色的水资源，将其合理循环利用尤为重要。

矿井水可回用资源量可通过富水系数及煤炭产量估算得出[23]；生活污水量根据羊场湾矿区统计数据得出；羊场湾矿区生态需水量以植被生态恢复过程耗水量为主，植被生态需水量的计算是根据羊场湾地区1968-2018年的气象数据，采用FAO-56 P-M公式计算逐月参考作物需水量[24]，再用系数法得到各阶段的实际需水量，最后累加得到植被总生态需水量。由此得出羊场湾矿区水资源优化配置供需平衡表，如表2所示。

表2 羊场湾矿区水资源优化配置供需平衡分析表 104 m3

4.2 参数获取

(1)确定性参数。供水系数ai反映了水源i相对于其他水源供水的优先程度；用水公平系数wj反映了用户j优先得到供水的次序。矿区水资源配置应优先最大限度利用再生水和矿井疏干水，其次利用地表水，减缓利用地下水，由此确定供水次序为再生水→矿井水→地表水→地下水。矿区遵循优先保证生活和生态需水的配置原则，确定用水次序为生活用水→生态用水→工业用水。利用以下公式计算，确定供水系数ai和用水公平系数wj。

(18)

(19)

式中：ni、ni max分别为供水水源i的供水次序和供水水源总数；mj、mj max分别为用户j的用水次序和用户总数。

通过计算得出再生水、矿井水、地表水、地下水的供水系数ai依次为0.4、0.3、0.2、0.1；生活、生态、工业的用水公平系数wj依次为0.50、0.33、0.17。另外，生活、生态、工业用水的排污系数依次为0.8、0.1、0.7。

根据《省级温室气体清单编制指南》，宁夏回族自治区单位耗电量的碳排放量(CO2)为0.977 kg/(kW·h)，按照羊场湾矿区单位供水年的耗电量和单位矿井水处理的年耗电量计算，工业水供水过程产生的碳排放量(CO2)为0.24 kg/m3、矿井水处理过程产生的碳排放量(CO2)为0.032 kg/m3。生活用水产生的碳排放量(CO2)取7.7 kg/m3，再生水回用的碳排放量(CO2)取-0.193 1 kg/m3，生态系统用水产生的碳排放量(CO2)取-2.2 kg/m3[25]。MUCC-GA模型中碳排放(CO2)系数的取值如表3所示。

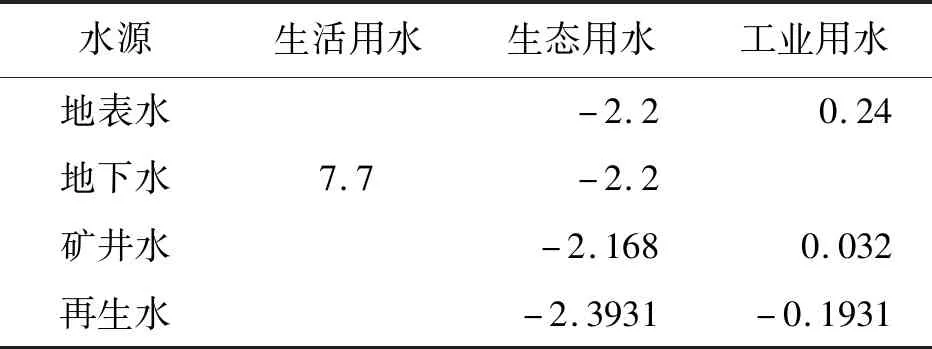
表3 MUCC-GA模型碳排放(CO2)系数取值 kg/m3

(2)不确定性参数。有关效益参数和费用参数的文献资料[26-28]表明，选取临近地区的供水效益系数[29]可以使模型更具典型性和代表性。结合不确定性基础理论，确定羊场湾矿区水资源优化配置模型在供用水过程中的不确定性参数效益系数和费用系数取值范围如表4所示。另外，生活用水、生态用水和工业用水过程的污染物排放量取值范围分别为[215,230]、[25,30]和[90,100] (mg/L)。

(3)需水量上下限。需水量上限定义为用水部门的最大需水量，下限则应综合考虑研究区的实际情况，以保障生活和生态用水为核心理念进行分类讨论。为满足居民生活的正常需求，保障居民用水供应量，生活需水保证率取100%；为推动矿区生态环境建设，改善植被重建环境，优先保证生态需水供应量，因此取其保证率为100%；为最大限度地满足生活和生态用水，取工业需水保证率为90%。最大的供水量不应大于需水量的110%，以节约用水并降低供水成本。

(4)遗传算法相关参数。本文实例研究采用第二代非支配排序遗传算法NSGA-Ⅱ，即在每一代进化过程中，对候选解进行非支配排序分层，并引入拥挤度计算和精英策略筛选个体。具体计算中设定初始个体数为50，进化代数为1×105。

表4 MUCC-GA模型不确定性参数取值 元/m3

4.3 MUCC-GA模型水资源配置结果与讨论

通过对模型进行函数分析，根据4.2节所述的参数选取，设置置信水平αi=0.85(i=1,2,3,4)、β1=β2=β3=0.8、γi=0.85(i=1,2,3,4)。通过遗传算法进行求解得到Pareto解集，以碳净排放量为目标与以污染物排放量为目标的Pareto解集对比见图3。

由图3可以看出，以碳净排放量为生态效益目标得出的年经济效益范围在162.3×104～163.7×104元之间，以污染物排放量为生态效益目标得出的年经济效益范围在153.2×104～180.4×104元之间，两者差值较小。而差异较大的为年缺水量，以碳净排放量为生态效益目标的年缺水量在-49.7×104～-43.5×104m3之间，代表在满足需水量的前提下还有富余的供水量，而以污染物排放量为生态效益目标的年缺水量在-49.6×104～35.8×104m3之间，其波动范围较大，且存在不满足需水要求的可能性。由此可得，将碳净排放量作为生态效益目标具有很强的实用性，且具有获得更优水资源配置方案的潜力。

在Pareto解集中，选取经济效益最高的为最优方案，从而得到该矿区水资源优化配置结果，如表5所示。该配置方案可同时带来以下效益：年经济效益为163.7×104元；年碳净吸收量(CO2)为534.5 t；年供水富余量为49.7×104m3。

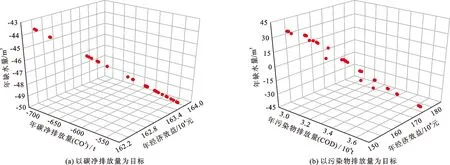
图3 不同生态目标函数的Pareto解集对比

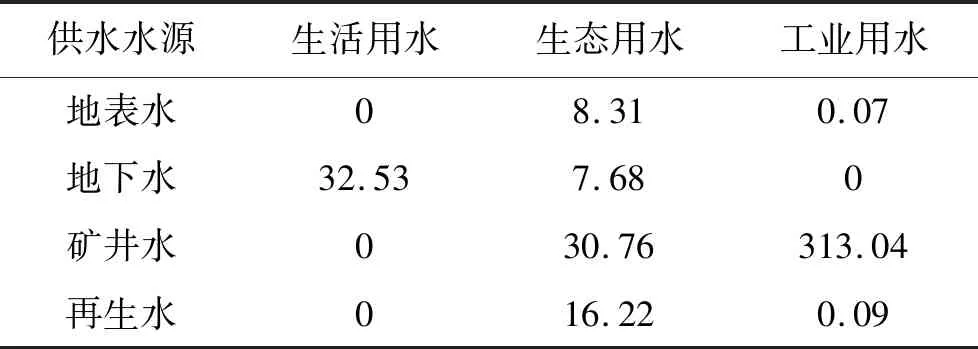
表5 基于MUCC-GA模型的羊场湾矿区水资源优化配置结果 104 m3/a

对羊场湾矿区水资源优化配置结果的分析讨论如下：

(1)工业用水是需水量最大的部门(表5)，工业部门的需水量占到了所有用水部门总需水量的约80%，着重控制工业用水量，推行节水政策，是减少总需水量最有效的途径。因此优化矿区工业产业结构，提高矿区工业用水效率，降低单位产量工业用水量是提高水资源利用效率的重中之重。

(2)生态用水以处理后的矿井水为主，可以避免占用地表水和地下水资源。充足的矿井水量可以填补干旱地区矿区修复面水资源的缺口，因此提高矿井水处理技术，解决矿井水回用的技术难题，是保证矿区生态恢复的基础。

(3)从工业用水的来源来看，增加矿井水的回用水量可以间接节约地表水资源，这不仅可以满足大量的工业用水需求，也符合水资源循环及再生利用的理念。对矿井水以及再生水的处理虽不能直接得到优质的水资源，但可以作为其他部门(如煤炭的洗选、灌溉用水等)的替代用水，从而间接地达到节水目的。

4.4 不同水资源规划模型的优化结果对比与分析

为了对比不同水资源规划模型的优缺点，分别从生态、经济、社会效益3个维度建立3个单目标优化配置模型，即以CO2净排放量最小化为主要目标的水资源优化配置模型(single objective-carbon emmission,SO-CE)、以经济效益最大化为主要目标的水资源优化配置模型(single objective-economic benefit,SO-EB)和以缺水量最小化为主要目标的水资源优化配置模型(single objective-water shortage,SO -WS)。将3个传统的单目标模型与遗传算法求解的多目标不确定性模型(MUCC-GA)的优化结果进行对比，结果如表6所示。

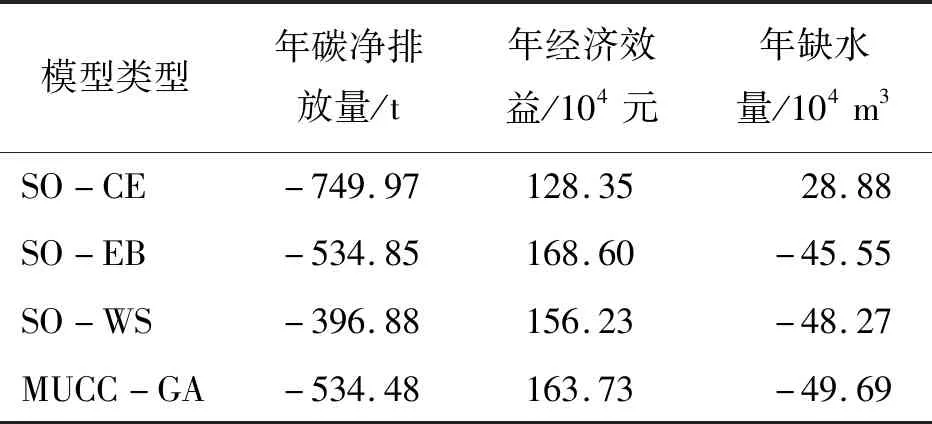
表6 4种水资源规划模型优化结果对比

由表6可以看出，SO-CE模型主要从碳净排放量最小的角度出发，所以其优化结果的碳净排放量为最少，但其年经济效益是4种配置模型中最低的，且存在区域供水不足的情况；SO-EB模型以经济效益为目标，其优化结果得到了最高的经济效益，但其区域供水富余量小于SO-WS和MUCC-GA模型；SO-WS模型主要从最大限度满足各区域需水量的角度出发，所得出的年缺水量与SO-CE和SO-EB模型相比为最少，但其碳净排放量是4种模型中最高的；MUCC-GA模型综合考虑了环境、经济与供水等因素，所得结果在保证较高水平经济效益的同时，区域供水富余量最高，还保有较低的碳净排放量。总体而言，SO-CE模型的优化方案体现了集中助力碳减排，加强碳吸收的要求；SO-EB模型的优化方案适用于对经济发展具有高需求的情景；SO-WS模型的优化方案适用于首要保证区域充足供水的情景，而当同时兼顾经济效益、碳排放与供水稳定因素时，MUCC-GA模型的优化结果是一种更为切实的方案。

5 结 论

利用遗传算法求解的多目标机会约束规划(MUCC-GA)模型能够反映复杂环境下的多目标性。本文将其应用于急需生态恢复的矿区水资源优化配置领域，在模型构造和求解中，客观反映了现实问题，较其他简单模型具有显著优势。本文所得结果满足了各用水单位的需求及供水约束，确保了经济效益和生态效益的综合最优，同时也探索了碳减排效益目标在矿区水资源配置中的适用性，可以作为制定羊场湾矿区水资源配置规划的科学决策依据，也可以为矿井水处理回用及矿区循环节水工作提供参考。

(1)通过羊场湾矿区水资源优化配置的案例研究表明，MUCC-GA模型在矿区水资源优化配置问题上有良好的适用性，利用遗传算法求解，可获取多个最佳配置结果，具有很强的灵活性。

(2)MUCC-GA模型得出的羊场湾矿区水资源优化配置方案中，工业用水量满足率达到100%，且存有富余供水量，因此该方案还可满足随着工业产值增加而带来的工业需水量的增长。对矿井水的处理和利用是保证充足工业用水的基础。

(3)碳排放目标体现了矿区碳减排的巨大潜力和生态意义，MUCC-GA模型相比于以污染物排放量为目标的模型，在保证经济效益不受损失的前提下，获得了更高的供水满足率，充分显示了将碳排放目标加入水资源优化配置的可行性。

(4)所得出的水资源优化配置方案充分体现出优先保障生活需水和生态环境用水、满足矿区工业平稳发展基本用水需求的配置原则，既可以改善矿区生态环境，又能够保证经济稳定发展，可为羊场湾矿区及其他相似地区的水资源管理提供借鉴。