乡镇编制总量实证研究——以重庆市为例

●重庆市委编办

乡镇是我国行政管理体系中最基层的行政单元。乡镇编制资源配置事关党的执政基础和基层政权建设。科学合理确定乡镇编制总量是统筹使用各类编制资源的重要前提。为探寻乡镇编制总量配置规律，合理确定乡镇编制规模，重庆市委编办以重庆市乡镇为样本开展实证研究。

一、重庆市乡镇实证研究的代表性

重庆市现辖38个区县、786个乡镇，其中建制镇625个，建制乡161个。一方面，重庆市具有中等省的规模，城乡差异大，是典型的“大城市、大农村、大山区、大库区”，统筹城乡发展任务重；另一方面，“直辖”之初主要沿袭原四川省辖市的格局，行政编制由原四川省所辖万州、涪陵、黔江和“老重庆市”行政编制数简单相加，“总盘子”偏小。“直辖”后，一直严控机构编制，乡镇编制总体比较精干。因此，以重庆市为例开展乡镇编制总量实证研究，对于全国其他地区精干高效配置乡镇编制资源和严格控制编外人员数量具有参考借鉴意义。

二、确定研究对象

乡镇编制总量管理的宗旨是合理确定乡镇人员编制规模。在当前实际工作中，乡镇存在以签订聘用（劳动）合同或劳务派遣协议形式聘用的从事技术性、辅助性、服务性等工作的编外人员。这类人员由国家财政负担经费。除涉及领导职务和保密、财务少数岗位外，乡镇编内人员与编外人员在工作岗位安排上并无明显区别，甚至在社会保障事务经办、综合行政执法辅助等领域，编外人员已成为重要力量。鉴于“编内不足编外补”的情况在乡镇普遍存在，“编内+编外”反映的是乡镇真实工作力量需求。将编内编外“一盘棋”统筹考虑，更符合基层工作实际，本文研究的乡镇编制总量是指乡镇综合办事机构和事业站所人员编制以及编外人员的总员额，即乡镇整体工作力量数。

需要说明的是，上级部门设在乡镇的派驻（出）机构，以及乡镇辖区内的中小学校和乡镇卫生院等单位的工作相对独立，且有单独的编制管理体系，其人员编制未纳入研究范围。

合理配备编制和聘用编外人员是为了保障乡镇机构正常履职。工作成效好、人员编制及工作力量配置精干高效的乡镇，编制资源和人力资源使用效益相对更高。本文以全市工作成效好、人员编制及工作力量配置精干高效的乡镇作为样本。

三、研究路径

（一）样本选取

乡镇年度综合目标考核结果能够一定程度反映乡镇工作成效，选取重庆市近3年工作成效好（2018—2020年度综合目标考核至少获得1次优秀）且人员编制及工作力量配置精干高效的乡镇作为样本。共收集360个乡镇样本，占全市乡镇总数的45.8%。

（二）收集影响因素

通过相关研究，影响乡镇编制总量的因素有：人口因素，涉及指标主要有常住人口、户籍人口、城镇人口、农业人口、少数民族人口、老龄人口等；城镇化发展因素，涉及指标主要有常住（户籍）人口城镇化率等；面积因素，涉及指标主要有地域面积、建成区面积、农业用地面积等；管理单元因素，涉及指标主要有村社区个数等；经济发展因素，涉及指标主要有GDP及人均GDP、市场主体数量、居民人均可支配收入等；财政保障因素，涉及指标主要有财政收入、一般公共预算收入等；社会自治水平因素，涉及指标主要有社会组织个数、城乡社区综合服务设施覆盖率等。此外，还有政治因素、文化因素、宗教因素、信息化水平、人员素质等其他影响因素。

实证研究坚持定性与定量分析相结合，充分征求相关专家意见，反复讨论筛选，最终确定收集的影响因素指标为：常住人口（X1）、城镇化率（X2）、地域面积（X3）、一般公共预算拨款收入（X4）、市场主体个数（X5）、村社区个数（X6）、社会组织个数（X7）。

（三）模型构建

以乡镇整体工作力量数（编制总数+编外人数）为研究对象，以常住人口（X1）、城镇化率（X2）、地域面积（X3）、一般公共预算拨款收入（X4）、市场主体个数（X5）、村社区个数（X6）、社会组织个数（X7）为影响因素构建模型。

乡镇整体工作力量数的理论公式可以简要表述如下：

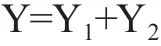
其中：Y——乡镇整体工作力量的测算结论数

Y1——测算理论数

Y2——调整数

理论公式表明，乡镇整体工作力量的“测算结论数Y”由“测算理论数Y1”和“调整数Y2”两部分构成。“测算理论数Y1”是指基于所收集乡镇样本的现实情况，利用模型推导出的理论数。考虑到乡镇整体工作力量数是编制总数与编外人数之和，较一般经济指标而言，其影响因素更为复杂，理论上无法穷尽所有影响因素，测算理论数与实际情况可能会存在一定偏差。因此，为了从技术上修正偏差，同时兼顾现实状况和工作实际，需要引入“调整数Y2”对“测算理论数Y1”进行适当修正，确保最终的“测算结论数Y”更为科学合理。

1.“测算理论数Y1”的模型构建

复杂的社会经济现象之间存在诸多联系，涉及多个变量之间的数量关系。如果变量之间存在密切而又不确定的数量关系，在大量统计资料基础上又可以判断这类变量之间的数量变化具有某种规律性，则这种变量之间的非确定性关系一般用回归分析的数学方法来处理。本研究中“测算理论数Y1”与影响因素X1～X7的关系属于这种情况，故采用多元线性回归方法构建模型。具体步骤如下：

（1）对样本进行异常值检验

基于模型稳健性考虑，本次研究使用spss软件，从是否有离群点、强影响点、高杠杆值的影响进行异常值检验，剔除42个异常样本后，形成318个乡镇组成的新样本。

（2）基于新样本，进行相关性分析

使用spss软件进行皮尔逊相关性分析，逐一分析X1～X7与当前乡镇整体工作力量数实际值（Y实际）的相关关系。相关性分析结果如表1所示。

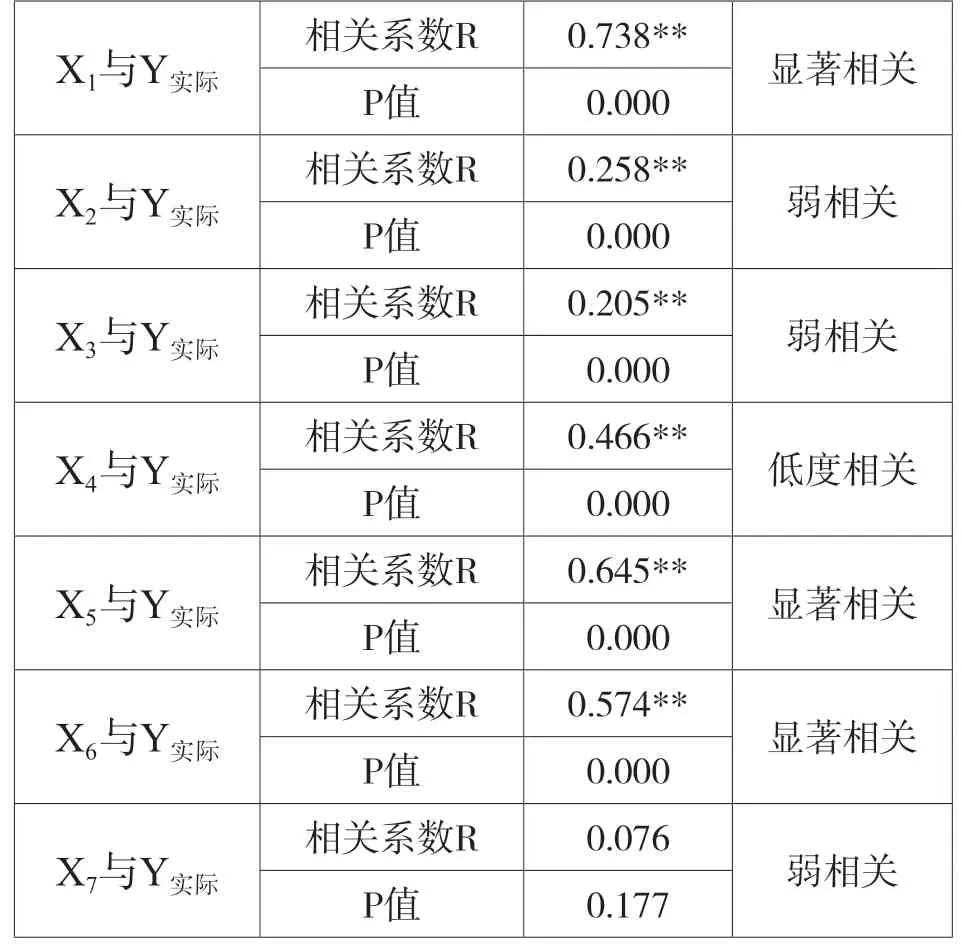
表1 基于318个样本，X1～X7与Y实际的相关性分析结果

需要说明的是，相关关系不等同于因果关系。相关性分析可以作为参考，而机构编制工作作为复杂的社会性管理工作，还需要联系实际具体分析，从而确定构建模型的因素指标。为此，本研究对相关指标作进一步分析。

常住人口（X1）相关系数最高，达到0.738，为显著相关。人口是一个国家、一个行政区域的基本构成要素，从古至今，人口因素皆是确定行政区划、配置官员或财政供养人员数量最基本的因素。常住人口能较为准确反映一个区域人口的真实数量，本研究采用该指标。

城镇化率（X2）相关系数仅为0.258，为弱相关。城镇化水平决定了地方政府管理事务的复杂程度，通常情况下城镇化率越高，社会分工就越细，对政府管理的要求也更高，政府工作力量也需加强。但相关性分析结果为弱相关，结合数据分布情况分析原因可能是，城镇化率需达到一定水平后才对乡镇整体工作力量数产生明显影响，本研究不采用该指标。

地域面积（X3）相关系数仅为0.205，为弱相关。地域面积历来是机构编制部门核定乡镇编制的重要指标。一般而言，地域面积与行政区域工作力量成正比，但此次相关性分析结果为弱相关，结合数据分布情况分析原因可能是，地域面积对工作力量的影响受到人口聚集程度和经济发展水平的客观影响。从地域面积指标的重要性考虑，经反复斟酌，本研究采用该指标。

一般公共预算拨款收入（X4）相关系数为0.466，为低度相关。政府机构运转、人员配备需要一定的财力作保障，且财政收入越高，越能承受人员规模的扩张，往往对编外人员聘用产生直接影响，与相关性分析结果一致。但从数据变化的角度看，近年来受疫情、经济大环境等影响，部分样本乡镇一般公共预算拨款收入每年变化差异较大，但乡镇整体工作力量数并未发生相应变化；从精干高效配置资源的角度出发，不能鼓励财政收入高就增加工作人员数量的做法，本研究不采用该指标。

市场主体个数（X5）相关系数为0.645，为显著相关。一个地区市场主体数量越多，反映该地区经济越发达，社会分工和协作越复杂，对管理服务力量的需求越高，与相关性分析结果一致。但考虑到此次收集的市场主体个数为企业个数与个体工商户户数简单相加，数量本身难以反映企业或个体工商户的规模、运营情况，本研究不采用该指标。

村社区个数（X6）相关系数为0.574，为显著相关。一个地区行政区划纵向的层级数和横向的单位数越多，都会使上下级或同级间关系越复杂，管理头绪增多、沟通成本增加，对工作力量的需求越高。村社区是乡镇最直接的管理单元，是影响乡镇工作力量配备的重要因素，本研究采用该指标。

社会组织个数（X7）P值不显著，为弱相关。社会组织数量一定程度反映一个区域的社会自治水平，一个地区社会自治水平越高，政府管理服务工作量就越少；反之，如果社会组织发展不成熟，一些公共服务职能无法从政府转移出去，势必需要政府加大人力资源投入。相关性分析结果为弱相关，结合数据分布情况分析原因可能是，多数样本乡镇的社会组织发展尚不成熟，对乡镇公共服务事项的承接功能还不明显，本研究不采用该指标。

综上，本次研究采用常住人口（X1）、地域面积（X3）、村社区个数（X6）3个指标构建模型。

（3）乡镇分类

确定分类方式。限于重庆市乡镇层面的数据可得性，本次研究难以用农业乡镇、工业乡镇等传统乡镇分类方式进行分类，而是从数据本身出发，选用聚类分析方法这一常用的客观分类法进行类别划分。

确定分类指标。采用常住人口（X1）指标作为唯一分类依据。主要基于以下考虑：一是指标选取的唯一性需要。基于乡镇样本数据分布的客观差异性，如人多面积大工作力量多、人多面积大工作力量少、人多面积小工作力量少等多种组合情况同时存在，如果选用多个指标进行分类，会导致每一类别有交叉，不适宜带入新样本合理分类。考虑简便操作，选用唯一指标有利于样本“对号入座”。二是人口指标的重要性论证。从机构编制管理实践看，人口一直是衡量乡镇工作量、确定编制规模最重要的考虑指标。从现实来看，将X1～X7与Y实际进行皮尔逊相关性分析，结果显示X1与Y实际的相关性最高。从国际国内应用看，日本定员管理的“定员模型”和“定员回归指标”都将人口作为核心指标；2014年国务院印发《关于调整城市规模划分标准的通知》也以常住人口为唯一统计口径划分城市类别。

分类结果与调整。使用spss软件，采用常住人口（X1）指标将318个样本进行聚类分析，结果显示，将样本分为四类相对合理。区间分布如下：

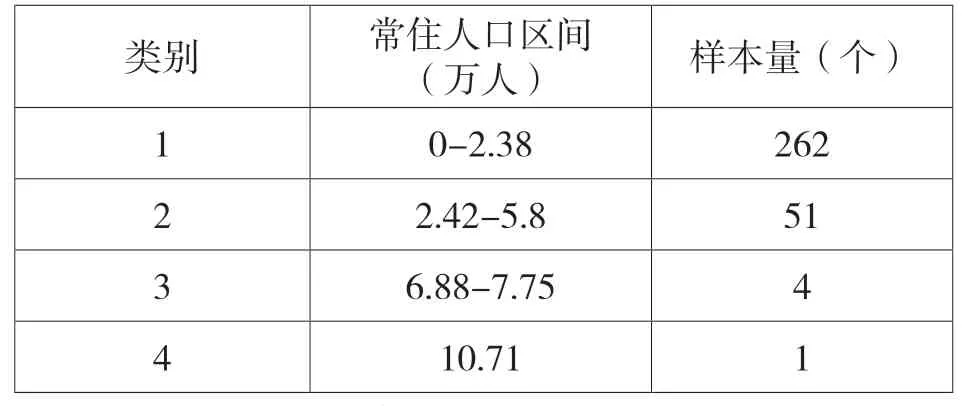
表2 按人口分四类

2014年国务院《关于调整城市规模划分标准的通知》规定：城区常住人口50万以下的城市为小城市，其中20万以上50万以下的城市为Ⅰ型小城市，20万以下的城市为Ⅱ型小城市；城区常住人口50万以上100万以下的城市为中等城市；城区常住人口100万以上500万以下的城市为大城市。考虑到城市规模划分标准主要对应地市级区域，与乡镇一级存在数量级的差别。将城市规模划分标准区间除以10倍量级，与重庆样本乡镇聚类分析的区间基本吻合，因此考虑结合该标准调整分类。调整后的分类区间及对应的样本数量如表3所示。

（4）初步构建模型

已明确因变量为乡镇整体工作力量数实际值（Y实际），采用的自变量为常住人口（X1）、地域面积（X3）、村社区个数（X6）。根据聚类分析结果，引入3个分类虚拟变量X8、X9、X10。

X8——当人口在0-2万时，X8=1，否则X8=0；

X9——当人口在2-5万时，X9=1，否则X9=0；

X10——当人口在5-10万时，X10=1，否则X10=0；

当人口在10万以上时，X8、X9、X10均为0。

将X1、X3、X6及虚拟变量X8、X9、X10与Y实际进行回归分析，结果如表4所示：

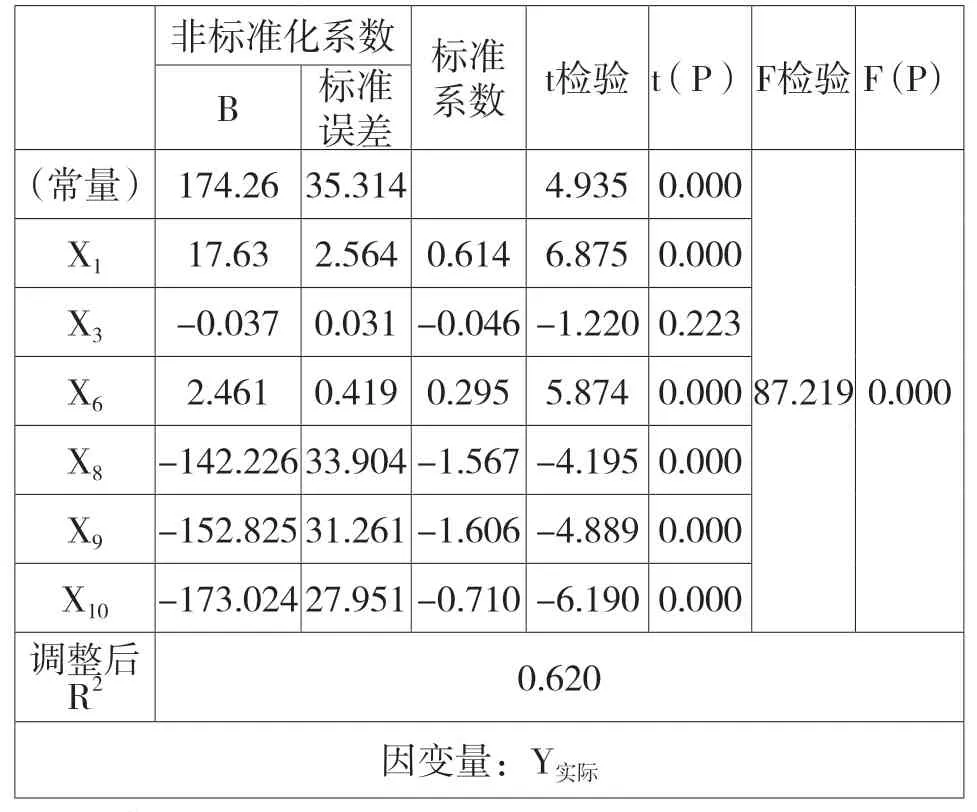
表4 按人口分四类回归分析结果

模型如下：

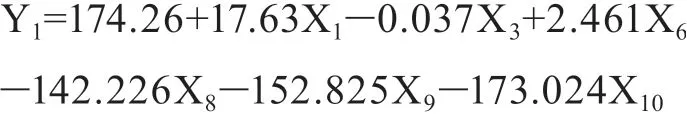
由表4可知，本模型中自变量对因变量的重要性排序依次为：X9、X8、X10、X1、X6、X3。分类虚拟变量对于模型的重要程度排在前列，说明分类效果较好。除X3的t检验显著性（P值）=0.223＞0.05不显著外，其余自变量的t检验显著性（P值）=0.000，具有显著意义。调整后R2=0.620，模型拟合效果较好。整体而言，该模型在统计学意义上成立，但地域面积（X3）在模型公式中呈现负相关关系，与乡镇编制总量管理实际情况不符，故对模型作进一步优化。

（5）对模型进行优化与调整

首先，尝试通过调整分类方式优化模型。在前述按人口分四类基础上，基于第四类10万以上仅1个乡镇样本，故将第三类与第四类合为一类。分三类后，引入X8、X9两个虚拟变量。将X1、X3、X6及虚拟变量X8、X9与Y实际进行回归分析，模型如下：

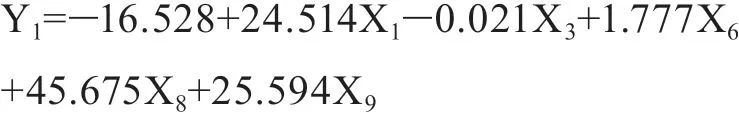
研究发现，地域面积（X3）仍为负相关，且常量的t检验P值不显著，故尝试剔除常量优化模型。

其次，尝试选用Eviews软件剔除常量优化模型。但研究发现，无论按人口分四类还是分三类，将X1、X3、X6及对应的分类虚拟变量与Y实际进行回归分析，地域面积（X3）始终为负相关。

最后，考虑到面积指标的现实重要性，经广泛征求意见和反复论证，本研究决定采用在机构编制管理实践中曾被多次采用的人口密度（Xa=X1/X3）替代地域面积（X3）进行研究。

人口密度（Xa）与Y实际的相关性分析结果如表5所示，相关系数R=0.430，相较于X3的相关性有所提升。

表5 基于318个样本，Xa与Y实际的相关性分析结果

用spss软件构建模型如下：

尝试1：按人口分四类，引入X8、X9、X10三个虚拟变量。将X1、Xa、X6及虚拟变量X8、X9、X10与Y实际进行回归分析，模型如下：

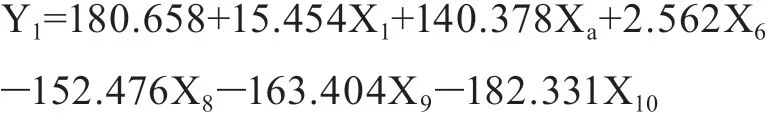
调整后R2=0.622

尝试2：按人口分三类，引入X8、X9两个虚拟变量。将X1、Xa、X6及虚拟变量X8、X9与Y实际进行回归分析，模型如下：

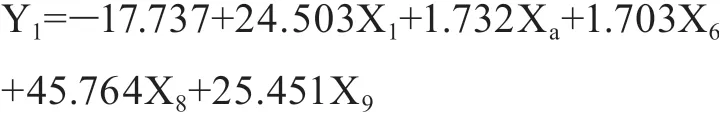
调整后R2=0.574

本研究使用Eviews软件进行同样操作，模型结果与spss软件结果一致。

上述两种分类方法得出的模型均符合实际情况。从调整后R2的比较而言，最优的模型是按人口分四类，即：

整体公式：

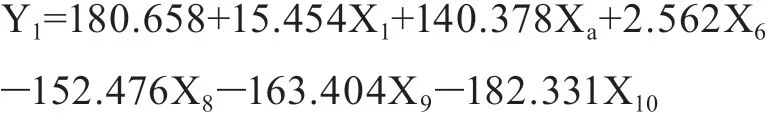
分类公式：

①当人口在0-2万时，X8=1，X9=0，X10=0，公式为：

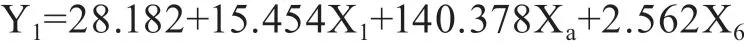
②当人口在2-5万时，X8=0，X9=1，X10=0，公式为：

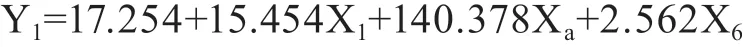
③当人口在5-10万时，X8=0，X9=0，X10=1，公式为：

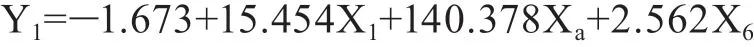
④当人口在10万以上时，X8=0，X9=0，X10=0，公式为：

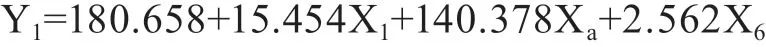
2.“调整数Y2”的确定

引入“调整数Y2”是为了修正“测算理论数Y1”与乡镇整体工作力量数实际值（Y实际）之间的偏差，得到更为科学合理的“测算结论数Y”。

将Y实际与“测算理论数Y1”的差值用Y*表示：

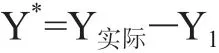
将Y实际与“测算理论数Y1”的偏差率用Y#表示：

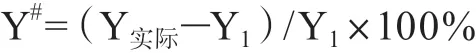
为提高“测算结论数Y”的适用性，应使得“调整数Y2”尽可能小，覆盖的乡镇样本尽可能多。本研究主要比较3种测算方法，择优确定调整数。

方法1：用多元线性回归方程的“标准误差e”作为调整数的取值依据。Y*的值在“标准误差e”正负区间范围内的乡镇样本数为该调整数能够覆盖的样本量。标准误差e可视为是该类机构编制规模的合理区间，凡在此区间内的编制即为基本合理。

方法2：用“3σ(西格玛)准则”中的“1σ”区间作为调整数的取值依据。Y*的“1σ”区间即调整数，其“1σ”区间范围内的乡镇样本数为该调整数能够覆盖的样本量。

“3σ准则”为：数值分布在（μ-σ,μ+σ)中的概率为68.26%；

数值分布在（μ-2σ,μ+2σ)中的概率为95.44%；

数值分布在（μ-3σ,μ+3σ)中的概率为99.74%。

其中：μ——一组检测数据的均值；

σ——一组检测数据的标准差。

方法3：基于机构编制管理实践，以乡镇样本覆盖率60%作为调整数的确定依据，在覆盖率60%的区间范围内Y#的最大取值即调整数。

综上，方法1、方法2所确定的调整数均为常数，调整区间是一个定值。常数之间可以根据“确定的常数尽可能小，覆盖的乡镇样本尽可能多”的原则进行比较。而方法3基于偏差率Y#来确定调整数，所得调整数为一个比例，调整区间随“测算理论数Y1”的变化而变化。比例与常数无法直接比较，需基于调整数所确定的区间之间的差距来比较，原则是“区间差距尽可能小，覆盖的乡镇样本尽可能多”。

（1）比较方法1与方法2

方法1：根据s p s s软件可知，该模型标准误差e=23.514，故调整数Y2=±23.514。Y*的范围在±23.514以内的有254个乡镇，占比79.87%。

方法2：经测算，Y*的“1σ”区间（μ-σ,μ+σ）为（-23.254，23.254）。故调整数Y2=±23.254。Y*的范围在±23.254以内的有253个乡镇，占比79.56%。

用方法1与方法2分别确定的常数项及其对乡镇的覆盖率相差无几，鉴于“3σ准则”在实证分析中的应用相对“标准误差e”更为广泛，故选择方法2。

（2）比较方法2与方法3

第一步，用方法2调整得出新的整体公式及分类公式。

方法2：对整体公式而言，理论上，样本数据分布在“1σ”区间的概率为68.26%，而本研究318个乡镇样本中，“1σ”区间实际已覆盖79.56%的样本。为进一步优化调整数，基于工作实际且方便与方法3比较，以覆盖60%左右的乡镇样本为目标，测算结果表明，“0.64σ”即可达到目标。

当取值区间为“0.64σ”时，调整数Y2=±14.88。Y*的范围在±14.8 8以内的有19 3个乡镇，占比60.69%。

方法2调整后整体公式如下：

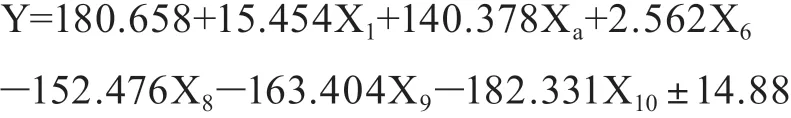
方法2：对分类公式而言，同理，以覆盖60%左右的乡镇样本为目标，测算结果如下：

①当人口在0-2万时，取值区间为“0.7σ”，调整数Y2=±13.08。Y*的范围在±13.08以内的有153个乡镇，占比62.45%。

②当人口在2-5万时，取值区间为“0.65σ”，调整数Y2=±22.93。Y*的范围在±22.93以内的有40个乡镇，占比62.5%。

③当人口在5-10万时，取值区间为“1σ”，调整数Y2=±28.98。Y*的范围在±28.98以内的有5个乡镇，占比62.5%。

需要说明的是：当人口在10万以上时仅1个乡镇样本，故以最接近的5-10万分类公式的调整数Y2=±28.98作为主要参考。

第二步，用方法3调整得出新的整体公式及分类公式。

方法3：对整体公式而言，以覆盖60%左右的乡镇样本为目标，当Y#=±20%时，能够覆盖188个乡镇，占比59.12%。

方法3调整后整体公式如下：

方法3：对分类公式而言，同理，以覆盖60%左右的乡镇样本为目标，测算结果表明：

①当人口在0-2万时，Y#=±19%，能够覆盖146个乡镇，占比59.59%。

②当人口在2-5万时，Y#=±22%，能够覆盖39个乡镇，占比60.94%。

③当人口在5-10万时，Y#=±24%，能够覆盖5个乡镇，占比62.5%。

需要说明的是：当人口在10万以上时仅1个乡镇样本，故以最接近的5-10万分类公式的调整数Y2=±24%作为主要参考。

第三步，方法2与方法3的适用性比较。

基于方法2和方法3调整得到新的整体公式及分类公式，分别随机代入0-2万、2-5万、5-10万各2个乡镇样本 进行“测算结论数Y”的区间测算。结果如表6所示。

表6 6个乡镇样本“测算结论数Y”的区间测算结果

?

从表6可知，方法2所得调整数是一个常数，区间差距是固定值，整体公式取整后区间差距始终是30。分类公式中，0-2万的公式取整后区间差距是26；2-5万的公式取整后区间差距是46；5-10万的公式取整后区间差距是58。方法3所得调整数是一个比例范围，测算区间随着Y1取值的变化而变化。当预测值Y1较小时，方法3所得区间差距比方法2更小，否则更大，甚至达到近80的情况，实际运用中可操作性不强，因此方法2更优。

（3）基于方法2，比较整体公式与分类公式调整数的适用性

整体公式在覆盖率约为60%的水平时，调整数Y2=±14.88。实际覆盖193个乡镇，占比60.69%。

分类公式在覆盖率约为60%的水平时：

0-2万调整数Y2=±13.08，实际覆盖153个乡镇，占比62.45%；

2-5万调整数Y2=±22.93，实际覆盖40个乡镇，占比62.5%；

5-10万调整数Y2=±28.98，实际覆盖5个乡镇，占比62.5%；

10万以上调整数Y2=±28.98，实际覆盖1个乡镇，占比100%。

综合而言，分类公式共可覆盖199个乡镇，占比62.58%。

虽然分类公式分别确定调整数后，相较整体公式能够多覆盖6个乡镇样本，覆盖率提升1.89%，但与此同时2-5万、5-10万的调整数却有较大比例的扩大，如5-10万的调整数为±28.98，是整体公式调整数±14.88的近2倍。从严控编内编外工作力量以及模型更为简便运用角度考虑，宜选用整体公式调整数确定最终模型。为进一步方便模型运用，本研究将调整数由±14.88四舍五入调整为±15。

四、小结

科学合理确定乡镇编制总量是机构编制管理的一道难题，本研究是基于重庆市乡镇实际进行的探索，研究过程中邀请了重庆市统计局专家、机构编制研究专家、部分区县编办同志、乡镇有关负责同志深度参与，确保既有专业理论支撑，又紧密贴合基层实际。基于乡镇编制总量管理的复杂性，研究工作坚持定量与定性分析相结合，注重“从实践中来、到实践中去”，根据重庆乡镇的特点科学选取影响因素指标构建模型。为体现模型适用性和可操作性，引入“调整数”进行修正，将乡镇编制总量测算值由一个点拓展为一个区间，在实际管理中灵活运用。具体来讲，乡镇现有编制总量在模型测算区间范围内或低于区间下限的，鼓励其继续保持精干高效的运行状态。乡镇现有编制总量超过模型测算区间上限的，应加强编制总量控制，指导乡镇加大内部挖潜力度，提高人员编制使用效益；同时，可结合实际，创造条件，对这类乡镇人员编制作适当精简。总而言之，各地乡镇情况差异较大，影响乡镇编制总量的因素不尽相同，本研究为乡镇编制总量提供研究参考，各地可结合本地区实际研究乡镇编制总量配置规律，为统筹使用乡镇各类编制资源、优化编制资源配置探索更多有效的路径和方法。