A Fully Distributed Hybrid Control Framework For Non-Differentiable Multi-Agent Optimization
2022-10-26XiaJiangXianlinZengJianSunSeniorJieChenandYueWei
Xia Jiang, Xianlin Zeng,, Jian Sun, Senior, Jie Chen,, and Yue Wei
Abstract—This paper develops a fully distributed hybrid control framework for distributed constrained optimization problems. The individual cost functions are non-differentiable and convex. Based on hybrid dynamical systems, we present a distributed state-dependent hybrid design to improve the transient performance of distributed primal-dual first-order optimization methods. The proposed framework consists of a distributed constrained continuous-time mapping in the form of a differential inclusion and a distributed discrete-time mapping triggered by the satisfaction of local jump set. With the semistability theory of hybrid dynamical systems, the paper proves that the hybrid control algorithm converges to one optimal solution instead of oscillating among different solutions. Numerical simulations illustrate better transient performance of the proposed hybrid algorithm compared with the results of the existing continuous-time algorithms.
I. INTRODUCTION
THE research of efficient algorithms to solve large-scale multi-agent optimization problems has attracted considerable interest [1]–[5], because of the rising of various distributed tasks, such as resource allocation in networks [6], [7],target tracking of sensor networks [8], [9], and control of UAV and autonomous vehicle [10], [11]. To achieve an optimial solution of the global problem, each agent in the network optimizes a local cost function subject to some constraints and communicates local variables with other agents by the connected topology [12]–[15]. In the literature, a large number of distributed discrete-time average-based algorithms appear to solve multi-agent optimization problems under various conditions and obtain fast convergence rate [13], [14],[16]. Recently, growing attention has been paid to the design of distributed continuous-time algorithms [6], [12], [17], [18],partly due to the wide applications of multi-agent optimization in continuous-time physics systems.
There have been some works studying continuous-time algorithms for large-scale non-differentiable optimization problems with local or coupled constraints. Non-differentiable optimization has wide applications in machine learning and economics. For instance, it is well-known that some nondifferentiable regular functions are often used in supervised learning to prevent overfitting. With the help of Lagrangian duality theory, numerous subgradient-based continuous-time primal-dual algorithms have been developed [19]–[21].Because of the non-differentiability of objective functions,existing distributed optimization algorithms are mostly firstorder methods, which often show degenerated convergence performance when the communication topology of multiagent network is sparse. To overcome this shortcoming,hybrid dynamical methods, which are composed of both continuous-time differential inclusions and discrete-time updating under certain conditions, may be a feasible choice to improve the dynamic performance of the existing first-order methods for distributed non-differentiable optimization problems.
For consensus problems in multi-agent systems, various hybrid dynamical systems have been studied [22]–[27], which own better convergence performance than continuous-time systems. However, for optimization problems, these distributed hybrid systems designed for consensus problems are not applicable because of the involvement of cost functions. Two recent hybrid works [28], [29] guarantee that local states converge to one global optimal solution with asymptotic convergence performance. Whereas, both of the algorithms in [28],[29] are not fully distributed because of supervisory resetting,which makes it difficult to be applied over large-scale multiagent networks with limited or expensive communication.Hence, it is necessary to design a fully distributed hybrid algorithm for multi-agent optimization problems.
Because of the mentioned wide applications and possible better convergence performance than continuous-time algorithms, this paper proposes a hybrid control framework for large-scale non-differentiable constrained distributed optimization problems over multi-agent networks. The contributions are summarized as follows.
1) This paper provides a fully distributed hybrid framework for solving the general large-scale constrained optimization problem, whose objective functions may be non-differentiable and non-strongly-convex. By introducing conflictavoidance rule in the jump mapping, each agent in the network updates local variables by local information and transmitted information from neighbors. To our best knowledge,this is the first work studying fully distributed state-dependent hybrid methods for non-differentiable optimization problems.
2) We provide complete and rigorous convergence proofs for the proposed distributed hybrid method with the invariance principle for hybrid dynamical systems. Because the objective function is non-strongly convex and non-differentiable, there may be a continuum of solutions to the optimization problem. With semistability theory, our proposed algorithm guarantees that the variables of different agents converge to one same optimal solution. This work has extended the existing hybrid works [22], [26], [30], [31] on consensus problems to distributed optimization problems. Compared with recent works for distributed optimization [28], [29], the proposed fully distributed framework does not need a supervisory resetting and reduces the network communication burden.
The framework of this paper is summarized as follows. The mathematical notations and the introduction of hybrid dynamical systems are introduced in Section II. The optimization problem description and the proposed distributed hybrid algorithm are given in Section III. The convergence property of the proposed hybrid method is proved theoretically in Section IV. Some numerical simulations are provided in Section V and the conclusion is made in Section VI.
II. PRELIMINARIES
A. Mathematical Notations

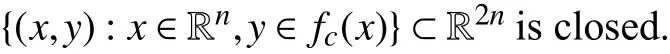
B. Graph Theory

C. Convex Analysis

D. Hybrid Dynamical System

To make the system (1) well defined, we introduce the following basic assumptions.
Assumption 1:
Basic assumptions of hybrid dynamical systems:

Remark 1:The invariance principle transcends stability analysis by characterizing the nature of the sets to which a bounded solution to a dynamical system converges. The basic invariance principle for dynamical systems has been extended to systems with non-unique solutions [35], in particular, differential inclusions. Lemma 2 involves a (Lyapunov-like)function that is nonincreasing along all trajectories that remain in a given set and further extends the basic invariance principle for hybrid dynamical systems, which is helpful for the following convergence analysis.
III. PROBLEM FORMULATION AND HyBRID ALGORITHM DESIGN
A. Problem Formulation

B. Distributed Hybrid Primal-Dual Algorithm Design



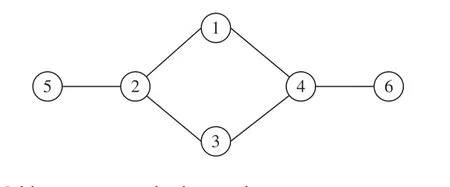
Fig. 1. Multi-agent communication topology.

Remark 5:The proposed algorithm (6), which is based on the primal-dual optimization framework, can be considered as an extension of the works [26], [28] and [36]. If there is no hybrid mechanism, the proposed algorithm is the same as the one in [36], which is a distributed continuous-time primaldual method. If the objective function and the first equality constraint of optimization problem (3) are absent, the proposed algorithm is the same as the work in [26], where variable estimates of different agents only achieve consensus.Compared with [28], this work further extends the optimization problems to non-differentiable optimization and improves the decentralized hybrid impulsive algorithm with supervisory resetting in [28] to a fully distributed hybrid design.
What’s more, although this paper focuses on problems over undirected graphs, it can be extended to multi-agent optimization over directed graphs. Some adjustments are needed to the continuous-time mapping, such as the works over directed graphs [37], [38]. The discrete-time mapping and conflictavoidance jump mapping can still be applied over directed graphs. The proof sketch is similar.
IV. CONVERGENCE RESULT




Remark 5:In brief, the line of proof for the convergence of the proposed algorithm can be summarized as following. At first, in Proposition 1, the variable states are proved to converge to one weakly invariant set and the equilibria of (11) are Lyapunov stable. In Proposition 2, it is further proved that variable states in the invariant set are equilibria of (11).Finally, with the help of semistability theory, any variable trajectory is proved to converge to one equilibrium point, which also means that any variable state converges to one optimal solution of problem (3).
V. SIMULATIONS
We consider a numerical simulation solving the distributed optimization problem (3) over an undirected connected network with 5 agents, which is demonstrated in Fig. 2. To make comparisons, we give another classical distributed continuoustime algorithm [40]–[42] to solve constrained problem (3) and the updating of each node is governed by

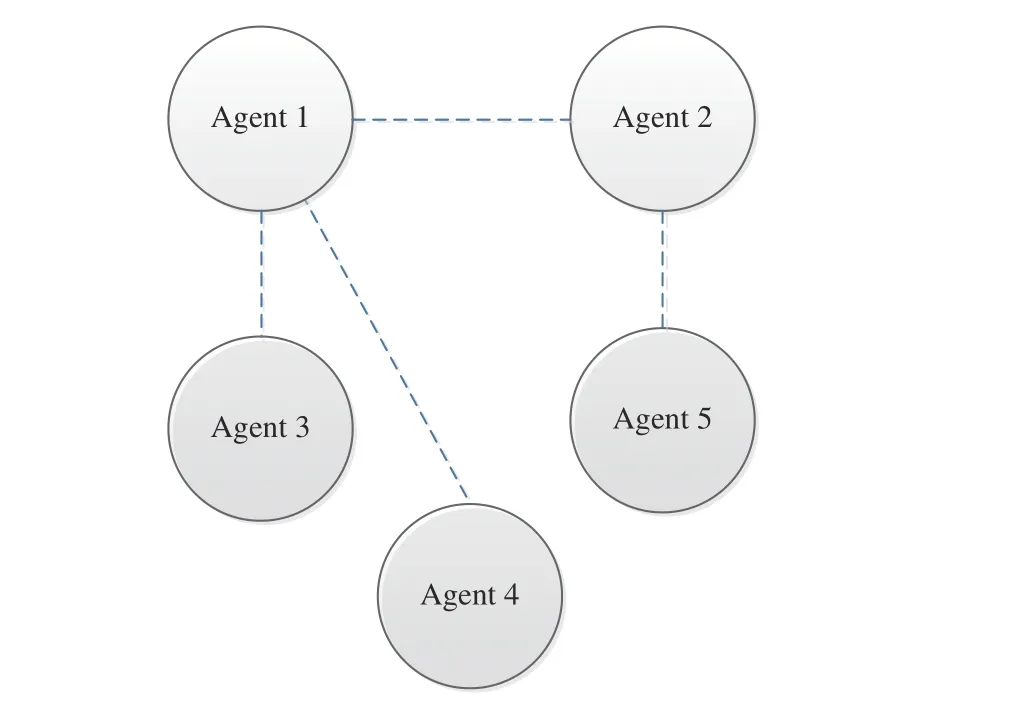
Fig. 2. Multi-agent network topology diagram.

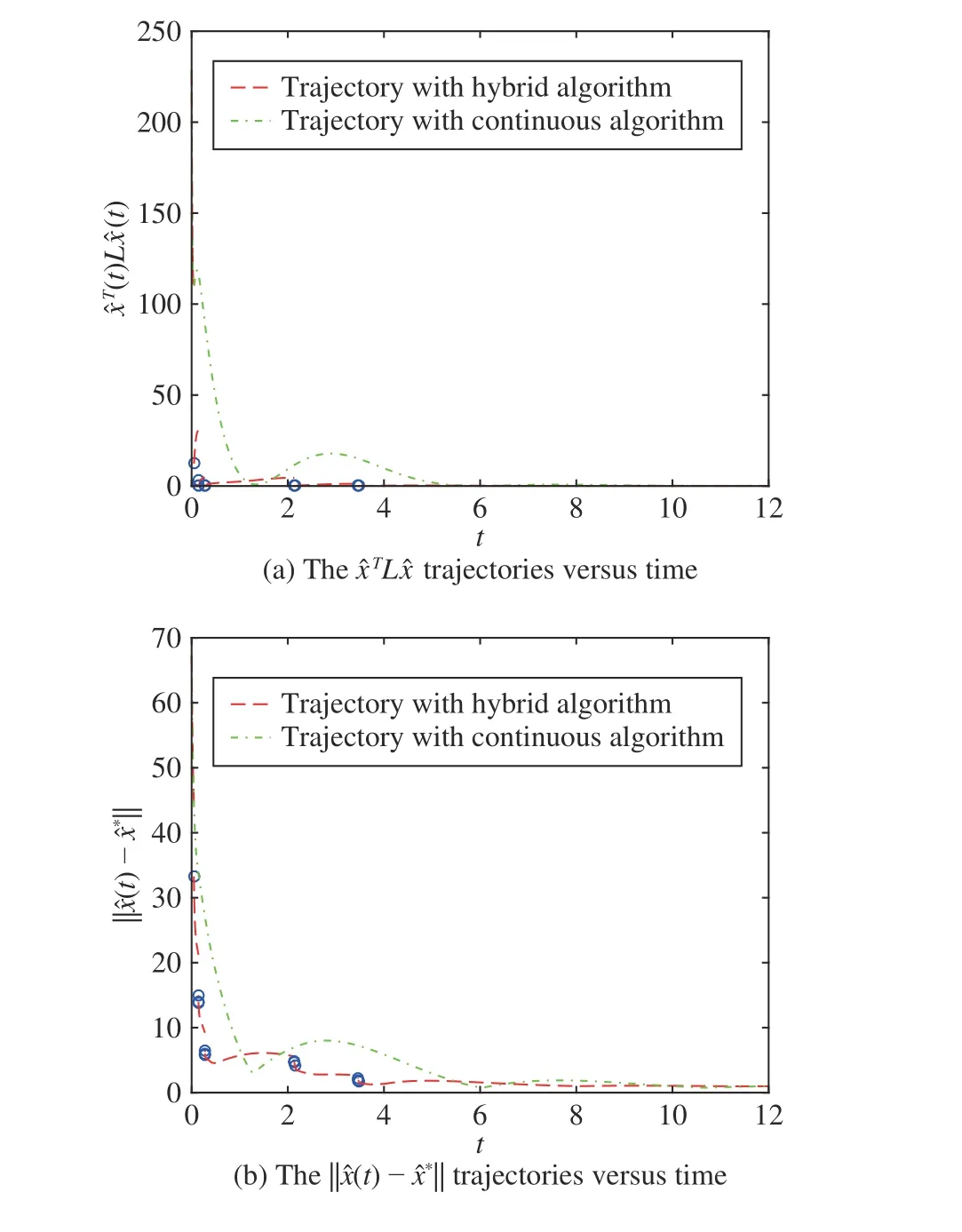
Fig. 3. Convergence results with algorithms (6) and (21).
VI. CONCLUSION
Inspired by the theory of hybrid systems, we have developed one fully distributed hybrid framework to improve the convergence performance of primal-dual continuous-time methods for large-scale multi-agent optimization problems.To obtain guaranteed convergence performance, we have designed state-dependent resetting and conflict-avoidance rule for the non-differentiable optimization problem, differently from most existing time-dependent works. With the semistability theory of hybrid dynamical systems, we have proved that variable states achieve a consensus and eventually converge to one optimal solution. Numerical simulations have shown that the proposed distributed state-dependent hybrid framework provides one feasible choice to improve the dynamic performance of distributed continuoustime algorithms. One important future direction is to develop one rigorous theoretical analysis to measure the improvement of the transient performance of distributed hybrid algorithms.
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Distributed Cooperative Learning for Discrete-Time Strict-Feedback Multi Agent Systems Over Directed Graphs
- An Adaptive Padding Correlation Filter With Group Feature Fusion for Robust Visual Tracking
- Interaction-Aware Cut-In Trajectory Prediction and Risk Assessment in Mixed Traffic
- Designing Discrete Predictor-Based Controllers for Networked Control Systems with Time-varying Delays: Application to A Visual Servo Inverted Pendulum System
- A New Noise-Tolerant Dual-Neural-Network Scheme for Robust Kinematic Control of Robotic Arms With Unknown Models
- Integrating Conjugate Gradients Into Evolutionary Algorithms for Large-Scale Continuous Multi-Objective Optimization
