Designing Discrete Predictor-Based Controllers for Networked Control Systems with Time-varying Delays: Application to A Visual Servo Inverted Pendulum System

Yang Deng, Vincent Léchappé, Changda Zhang, Emmanuel Moulay, Dajun Du,Franck Plestan,, and Qing-Long Han,

Abstract—A discrete predictor-based control method is developed for a class of linear time-invariant networked control systems with a sensor-to-controller time-varying delay and a controller-to-actuator uncertain constant delay, which can be potentially applied to vision-based control systems. The control scheme is composed of a state prediction and a discrete predictor-based controller. The state prediction is used to compensate for the effect of the sensor-to-controller delay, and the system can be stabilized by the discrete predictor-based controller. Moreover, it is shown that the control scheme is also robust with respect to slight message rejections. Finally, the main theoretical results are illustrated by simulation results and experimental results based on a networked visual servo inverted pendulum system.

I. INTRODUCTION

A. Motivations

VISION-BASED sensors are widely used in various con

trol applications (e.g., self-driving cars [1], [2], robots[3], UAVs [4], and inverted pendulums [5]–[7]) due to their low cost (compared with LIDAR [2, pp.176]) and the rapid progress of image-processing-based sensing techniques (e.g.,indoor navigation [8], collision avoidance [9]). In such a control system, state information can be resolved from the sampled images captured by a camera [3, pp.132] by using an image-processing algorithm. After resolution, the state information is available for the controller design, and it is transmitted to the controller through a wired or wireless sensor-to-controller communication channel that is subject to a small uncertain time-varying transmission delay of several milliseconds[10, pp.147]. After receiving state information, the controller updates the control signal and sends it to the actuator with the help of the controller-to-actuator channel. Finally, the updated control input is applied to the controlled plant. Based on the previous statements, the whole control process of such a system is subject to the following time-delays:

● the exposure time of the camera (constant);

● the computational delay introduced by the image-processing algorithm (long, time-varying);

● the transmission latency induced from the sensor-to-controller communication channel (small, time-varying);

● the computation time of the control algorithm (small, constant);

● the transmission latency induced from the controller-toactuator communication channel (small, time-varying);

● the physical dead time of the actuator (constant).

Note that the time-delays introduced by data communication are time-varying because of network congestion, the communication protocol, and the real-time intensity of the communication network. The computational time of the imageprocessing algorithm is also time-varying since it is usually affected by the number of feature points in each frame, the number of image edges in each frame, and the real-time illumination intensity.

Based on the discussions above, the vision-based control system can be modeled as a networked control system (NCS)[11] with sensor-to-controller time-varying delay and the controller-to-actuator uncertain constant delay1The controller-to-actuator delay is the sum of a constant delay (dead time of the actuator) and a small time-varying delay (controller-to-actuator data transmission latency). Therefore, it can be equivalently modeled as an uncertain constant delay.. Thus, due to its high potential for application (e.g., an indoor mobile robot, or a UAV in weak GPS environment [4]), it is important to develop new control strategies to stabilize the system.

B. Interests of the Discrete-Time Method

Some discussions are given in this subsection in order to explain the reason why the discrete-time control method is adopted. The main challenges for the vision-based control systems mentioned in Section I-A are given in the sequel:

Problem 1: The image-processing algorithm needs a long computational time (compared with the transmission delays).As a result, a long sensor-to-controller time-varying delay is introduced [6], [12];

Problem 2: The vision-based control system can only run at a low sampling rate. Indeed, the sampling rate of such a system depends on the frame rate of the camera and the computational time of the image-processing algorithm. On the one hand, if the frame rate is high, then the quality of the captured images will be lower (i.e., low-contrast [5, pp.8138]), and it may introduce more measurement errors. On the other hand, a high sampling rate will make unprocessed images accumulate if no distributed computation is applied [13, pp.554], and this problem will make the control task more complicated.

After discussing the main issues of the vision-based control systems modeled as an NCS, three main control solution to NCSs [14], [15] are recalled:

● Discrete-time method [16]–[18]: This method turns the original NCS into a discrete-time extended system, where the control law is designed for the extended system in the discrete-time domain;

● Impulsive system method [19]: Using this method, an NCS is considered as a hybrid system (i.e., continuous-time system with state jumps), and the discontinuous Lyapunov functional is used for the stability analysis;

● Time-delay method [20]–[23]: This method treats the effects of sampling & ZOH (zero-order hold) as a time-varying delay, where a Lyapunov-Krasovskii stability analysis is provided.

To solve Problem 1, predictor-based controllers designed by using the discrete-time method [18] and the time-delay method [24] are able to deal with long time-delays, whereas the impulsive system method is not effective.

Next, the arguments given in [15, pp.61] explain that the discrete-time method is less conservative in the maximum allowable transmission interval (MATI) for linear time-invariant (LTI) networked control systems, which indicates that this method can stabilize the LTI networked control systems with a lower sampling rate. Thus, it can better meet the requirement of Problem 2.

In conclusion, the discrete-time method can solve Problems 1 and 2 together, and is suitable for LTI vision-based control systems. Therefore, the main objective of this paper is to develop a discrete predictor-based control technique for a class of LTI networked control systems, and then implement the control algorithm on a real vision-based control system.

C. Contributions and Organizations

This paper proposes a control solution to stabilize NCSs with sensor-to-controller time-varying delay and controller-toactuator uncertain constant delay, which can be applied to vision-based control systems. The controller design is based on the discrete-time extended system representation [16]–[18],[25] in order to deal with long time-delays and a long sampling period. The message rejection (packet disordering) is also considered. The main theoretical contribution of this paper is threefold:

● Compared with [18], where the network-induced delay is a constant, this paper considers that the network-induced delay is time-varying;

● In [25], discrete predictor-based control of the sampleddata system with a single uncertain constant input-delay is developed, but the explicit upper bound on the allowable delay uncertainty is not given; this bound is calculated in detail by this paper;

● The effects of the time-varying delays are analyzed in[17], [26], but they did not consider the effect of message rejection (packet disordering) caused by the time-varying delays, whereas the proposed method deals with the message rejection phenomenon in the sensor-to-controller channel.

Furthermore, the proposed control scheme is implemented on the networked inverted pendulum visual servo system(NIPVSS) introduced in [6], [7], the experimental results are given in Section VII.

In conclusion, this paper provides a control scheme for vision-based control systems (which can be modeled as a class of LTI networked control systems with time-varying delays),and the proposed method has the following main features:

● The state prediction technique is used to compensate for the effects of sensor-to-controller time-varying delay, and also deals with slight message rejection.

● The discrete predictor-based controller is designed to stabilize the LTI plant that is subject to controller-to-actuator uncertain constant delay. The benefit of this control algorithm is lower conservativeness in the sense of MATI, as stated in Section I-B.

● The experimental validation of the proposed control technique on the NIPVSS test bench illustrates that the proposed method is able and suitable to cope with the real visual servo control problem. Moreover, based on the experimental results presented in Section VII-C, it is observed that the proposed method can provide better control performance than the nonpredictive control method.

The rest of the paper is organized as follows. The problem statement is given in Section II in order to explain modeling and some necessary assumptions. The extended system representation, the state prediction technique, and the discrete predictor-based controller are introduced in Section III. The main theoretical results for the unperturbed plant are presented in Section IV. Then the theoretical results are extended to the case with external disturbances in Section V, and they are illustrated by simulation results of Section VI and experimental results provided in Section VII. Finally, a conclusion is presented in Section VIII.

II. PROBLEM STATEMENT

A. Notations

In this paper, the following notations are used. The symbols N and N+represent the sets of non-negative integers and strictly positive integers. The set of all real matrices withmrows andncolumns reads as Rm×n. The identity matrix of sizem×mwrites asIm. The superscript “T” denotes the matrix transposition. The symbol ‖·‖ gives the Euclidean norm of a vector and the 2-norm of a matrix, respectively. Finally, the maximum and minimum eigenvalues of a symmetric matrix read as λmax(·) and λmin(·).

B. System Modeling

In this subsection, the modeling of the LTI networked control system for the LTI vision-based control system (as described in Section I-A) is introduced. Consider the following LTI plant:

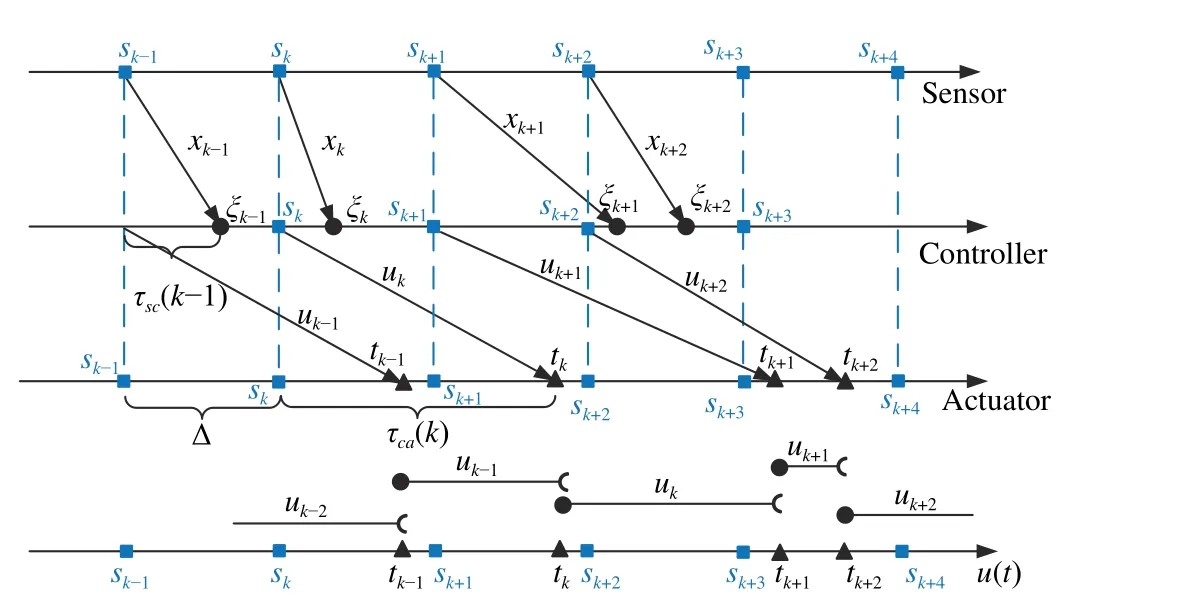
Fig. 1. Timing diagram of the control scheme with time-driven sensor,time-driven controller and event-driven actuator.

Remark 2:The Zeno phenomenon never occurs since the updates of the state measurement and the control law are periodic.

In [22], it is assumed that the older control inputs and the older state measurements cannot arrive at the destination later than a newer one. In other words, the sequences {tk}k∈Nand{ξk}k∈Nare strictly increasing:

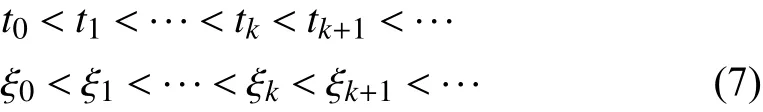
in order to avoid message rejection (packet disordering). In this paper, only a weaker assumption is required as below.

Assumption 2:The sequence {tk}k∈Nis supposed to be strictly increasing.

Assumption 2 can also be ensured by (4), (5), and (6) due to the fact that τca(k-1)＜τca(k)+Δ is always ensured by these inequalities. This assumption shows that the proposed method deals with slight message rejection in the sensor-to-controller channel.

III. ExTENDED SySTEM REPRESENTATION AND DISCRETE PREDICTOR-BASED CONTROLLER

In this section, the extended system representation and the discrete predictor-based controller are introduced. Section IIIA presents the control scheme with a controller-to-actuator constant delay. Section III-B considers the case when the controller-to-actuator delay is uncertain constant.

A. Controller-to-Actuator Constant Delay Case

The controllability of (9) and the controllability of (10) are equivalent since (9) and (10) are two different descriptions of the same system, see [18, Remark 5]. Therefore, the controllability of the extended system (10) can be guaranteed if Assumption 1 is satisfied. It is the possible to find a statefeedback control law

The state prediction technique (13) is able to deal with slight message rejection [16, pp.1576] (packet disordering [32,pp.1775]) in the sensor-to-controller network. In the communication channel, if an older data packet arrives at its destination after a newer packet, then this older one is discarded in order to ensure that the newest data is processed. This phenomenon is presented in Fig. 2, where the measurementsx(sk)andx(sk+1) are neglected due to message rejection since they arrive at the controller after the measurementx(sk+2).

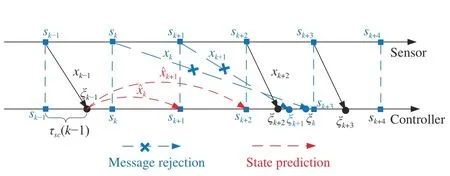
Fig. 2. Timing diagram of the sensor-to-controller channel with message rejections.

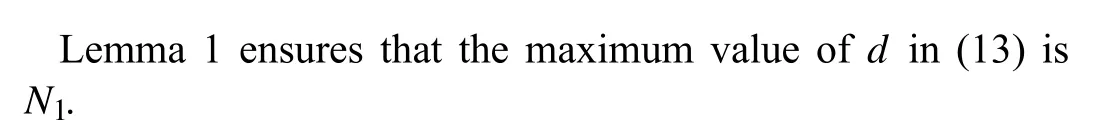
B. Controller-to-Actuator Uncertain Delay Case

In this subsection, we develop the technique given in Section III-A, and take into account the delay uncertainty in the controller-to-actuator channel. Consider (5) and (6). The controller-to-actuator delay satisfies

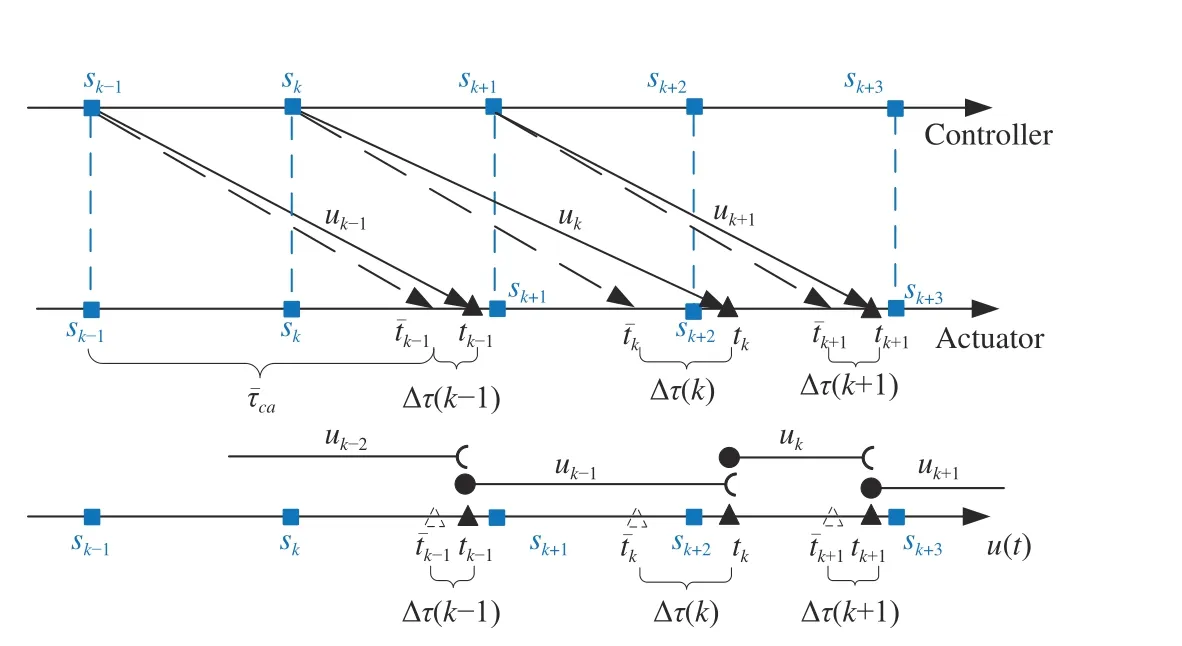
Fig. 3. Timing diagram of the controller-to-actuator channel with uncertain delays.

Taking the difference between (39) and (38), one can calculate the 2-step estimation error as follows:

IV. MAIN THEORETICAL RESULTS

The main theoretical results of this work are presented in this section. Before stating the main convergence result of this work, one uses the results given in Lemmas 1–3 to find the upper bound on the estimation error (41).

Lemma 4:Consider the extended states

Theorem 1 provides a discrete-time control scheme for a class of NCSs with sensor-to-controller time-varying delay,and the robustness to delay uncertainty is also analyzed.

V. RESULTS WITH ExTERNAL DISTURBANCE

In Corollary 1, the input-to-state stability of the discretetime extended system is obtained, which implies that the proposed method can deal with the case when the system plant is perturbed by a uniformly bounded external disturbance.

①课程内容按照学科知识点的逻辑顺序组织。为了促进学生主动思维能力的发展，教师设定每个知识单元学习目标和完成标准，指引学生跟随任务完成学习。如在教学三相异步电动机的正反转控制时，教师事先提出预习思考题：异步电动机的转动原理是什么？如何实现异步电动机的正转和反转？使学生带着学习目标学习并思考。

VI. SIMULATION RESULTS

In this section, some simulation results are provided to demonstrate the benefits of the proposed control method based on the discrete-time approach, i.e., it is able to stabilize the NCS under a low sampling rate, as described in Section I-B.Moreover, the message rejection is also considered in the simulation, and it is compensated by the proposed state prediction technique (13).

Consider the continuous-time unperturbed plant

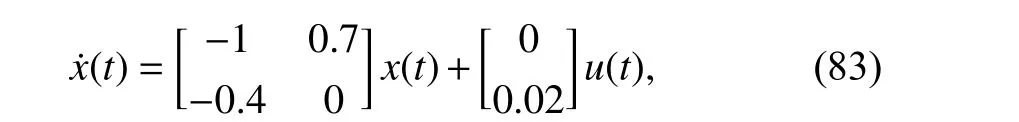
and the continuous-time perturbed plant Namely, under the 1-step state prediction and the 2-step state prediction, the complete control laws are computed as follows:

The simulation results presented in this section verify the following contributions of Theorem 1 and Corollary 1:

● The state prediction technique (13) is able to deal with slight sensor-to-controller message rejections;

● Due to the properties of the discrete-time approach [16],[18], the proposed method provides endurance even with a long sampling period;

● The control technique is able to cope with a uniformly bounded external disturbance, and the ISS stability/ convergence is illustrated by the simulation results.

Furthermore, the calculation of the maximum allowable delay uncertainty μ*in Theorem 1 is conservative, and the choice of the feedback matrix K can be more flexible in practice.

VII. ExPERIMENTAL VALIDATION ON NIPVSS

In this section, the main theoretical results of Theorem 1 are implemented on the NIPVSS test bench [6], [7] in order to test the effectiveness and the performance of the proposed control method on a real vision-based control system.

A. Configuration of the NIPVSS Test Bench

In this subsection, the NIPVSS test bench [6], [7] is introduced. The test bench is firstly composed of an inverted pendulum displayed in Fig. 5. The movement of the inverted pendulum is captured by anAca640-120gmmonochrome industrial camera (see Fig. 6), after which the state informationx(sk)is obtained by the image-processing algorithm (based onMicrosoft Visual Studio 2010andOpenCV 2.4.11) on each frame. In this experimental set-up, the cart position is obtained by applying the translation between the pixel coordinate system and the world coordinate system since the camera and the moving plane are fixed. The pendulum angle is measured in the pixel coordinate system by using the edge detection technique based on the Hough Transformation [37]. Once the controller (i.e., a host computer) receives the vision-based state measurements through the communication channel, it runs the control algorithm and then sends the control signal to aGT-400-SV-PCImovement control card. Finally, aMSDA023A1Aservo driver receives the control signal and drives the cart to move on the rail.

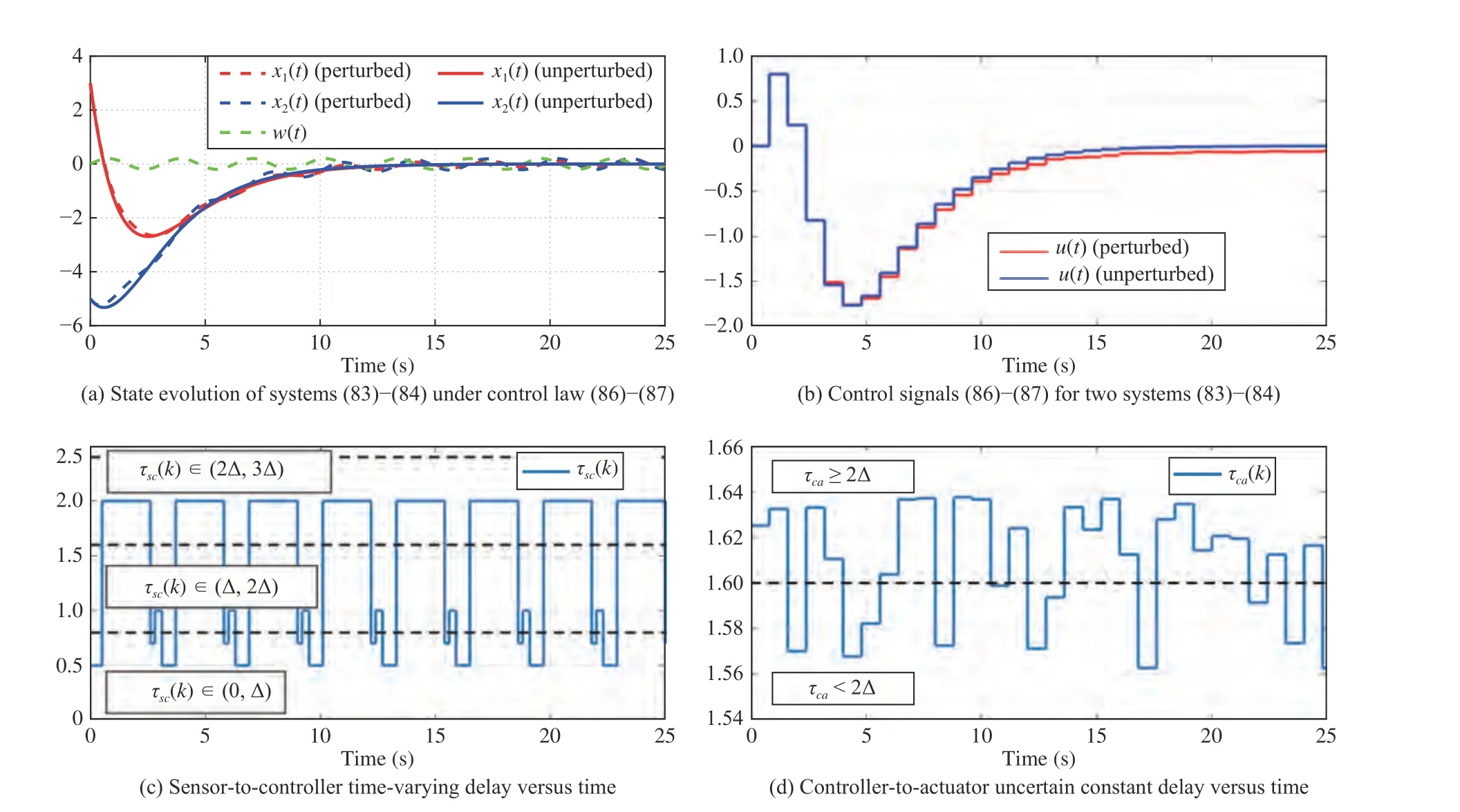
Fig. 4. State evolution, control signal, and network-induced delays versus time for the unperturbed/perturbed systems (83)–(84).

B. Controller Design for NIPVSS Based on Theorem 1

The controller design is based on the linearized inverted pendulum plant around the straight-up position

Fig. 5. The experimental set-up of the NIPVSS.

Fig. 6. Control diagram of the NIPVSS.

TABLE I MODEL PARAMETERS OF THE INVERTED PENDULUM (REPRINT FROM [7, TABLE 1])

Note that the max frame rate of the industrial camera is 120 Hz, i.e., the industrial camera can maximumly take120 photos per second, but the image-processing algorithm cannot follow up with this sampling rate. Indeed, by considering the image-processing timeD(t), the image-processing algorithm cannot process more than 1 /0.015=66.67 frames per second.In the experiment, the sampling period is set to Δ=0.02 s in order to ensure that each frame is captured after the state information resolution of the previous frame, and a similar discussion is given in [13, pp.554].

C. Experimental Results

The experimental results4The videos of the two experiments are available at https://drive.google.com/drive/folders/1WEp7VUt5JTcUlbQf6cAt4z4ZHKKJzGjN?usp = sharing.are presented in Fig. 7. Firstly,Fig. 7(b) shows that the two methods can achieve good control performance on the pendulum angle θ(t): it is maintained in a neighborhood around zero (namely, the curves are almost bounded over [ -0.04 rad,0.04 rad]). Secondly, the experimental results displayed in Fig. 7(a) show that the cart position α(t) cannot return perfectly to the original position (α (t)=0)due to the measurement error introduced by the image-processing algorithm [7, Remarks 3–4] and the imperfect linearized modeling of (90). However, the experimental results still confirm that the proposed method provides better control performance on the cart position than the LQR controller.

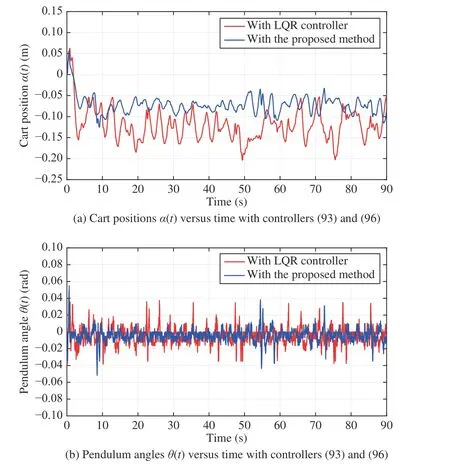
Fig. 7. Experimental results with the LQR controller (96) and the proposed controller (93)–(95).

Next, as done in [7, Section V-B], the following indexes are used for the analysis of the results presented in Fig. 7:

● MCP: mean of cart position;

● SCP: standard deviation of cart position;

● MPA: mean of pendulum angle;

● SPA: standard deviation of pendulum angle.

The normalized (with respect to LQR controller (96)) performance indexes of the two controllers (93) and (96) are provided in Fig. 8: smaller the value is, better the result is. Apparently, the results obtained by the proposed controller (93) are better than the ones obtained by the LQR method (96).

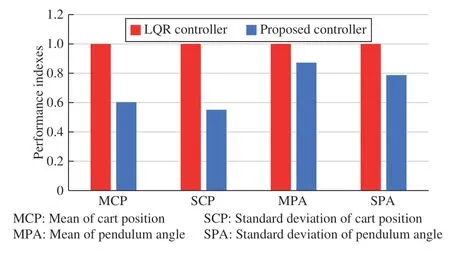
Fig. 8. Normalized (with respect to LQR controller) performance indexes of the experimental results.

The experimental results displayed by Figs. 7–8 illustrate that the proposed method is successfully implemented on the real remote visual servo control system. Moreover, the proposed method provides better experimental control performance than the non-predictive control solution (96). Furthermore, the proposed method has good control performances on such a fast motion control system, which shows that the proposed method has wide application prospects in control engineering.

VIII. CONCLUSIONS

A discrete-time control solution (state prediction and discrete predictor-based controller) is designed to stabilize a class of LTI networked control systems, and this method is applied to a networked visual servo inverted pendulum system. The state prediction technique is used to deal with the sensor-tocontroller time-varying delay, and the uncertain constant controller-to-actuator delay is compensated for using the predictor-based controller. Moreover, the message rejection phenomenon is also considered in this work. The theoretical results are illustrated by the simulation and experimental results. In the future, the following research activities will be investigated:

● Theoretical part: the output-feedback control technique will be developed, some additional network-induced imperfections (e.g., quantization [18], [40], cyber-attack [41], [42])will be considered, and the stochastic Lyapunov approaches will be applied in order to systematically deal with stochastic packet-dropout and message rejection at the same time.Besides, more analysis will be given in order to relax the assumption Δτ(k)∈(0,Δ], and the controller-to-actuator message rejection will be studied as well.

● Experimental part: in order to improve the control performance of the cart position, the robustH∞control technique will be used to calculate the feedback gain K in a more systematic way.