A New Noise-Tolerant Dual-Neural-Network Scheme for Robust Kinematic Control of Robotic Arms With Unknown Models

Ning Tan,, Peng Yu, Zhiyan Zhong, and Fenglei Ni

Abstract—Taking advantage of their inherent dexterity, robotic arms are competent in completing many tasks efficiently. As a result of the modeling complexity and kinematic uncertainty of robotic arms, model-free control paradigm has been proposed and investigated extensively. However, robust model-free control of robotic arms in the presence of noise interference remains a problem worth studying. In this paper, we first propose a new kind of zeroing neural network (ZNN), i.e., integration-enhanced noise-tolerant ZNN (IENT-ZNN) with integration-enhanced noisetolerant capability. Then, a unified dual IENT-ZNN scheme based on the proposed IENT-ZNN is presented for the kinematic control problem of both rigid-link and continuum robotic arms,which improves the performance of robotic arms with the disturbance of noise, without knowing the structural parameters of the robotic arms. The finite-time convergence and robustness of the proposed control scheme are proven by theoretical analysis.Finally, simulation studies and experimental demonstrations verify that the proposed control scheme is feasible in the kinematic control of different robotic arms and can achieve better results in terms of accuracy and robustness.

I. INTRODUCTION

DUE to their outstanding capability to work continuously and efficiently, robotic arms are expected to replace humans to accomplish arduous and repetitive assignments and have attracted the interest of many researchers. Despite significant progress in the research of robotic arm control [1]–[8],conventional methods rely heavily on the precise kinematic or dynamic models of robotic arms [9]–[13], which restricts the applications of these methods on robotic arms with unknown models and the transfer of these methods among different robotic arms. Although there are a lot of calibration technologies that can avoid uncertainties [14], calibration is usually performed before the robot begins work. Uncertain factors that only appear during the working process of the robot can also lead to the degradation of model-based control system performance. Therefore, these restrictions have necessitated the emergence of model-free control schemes for robotic arms.

With this in mind, many model-free control algorithms for robotic arms have been developed [15]–[18]. For example,Leeet al. [19] achieved the control of a soft robot manipulator based on nonparametric online learning which facilitates effective endoscopic navigation. To make robot manipulators work in unstructured environments, Thuruthelet al. [20] proposed a closed loop kinematic controller based on a machine learning approach. Liet al. [21] presented a model-free control method based on an adaptive Kalman filter for robot manipulators to solve the trajectory tracking problem. In spite of the advances in the model-free control of robotic arms, previous studies suffer from the limitations of low accuracy and poor robustness. As a result, researchers are dedicated to achieving better performance for the control of robotic arms with unknown models.

The research of neural networks and artificial intelligence has made great progress in recent years [22]. There are many applications of neural networks in robotics as a result of the convenience of hardware implementation and self-learning capability [23]–[26]. For instance, recurrent neural networks(RNN) were employed to solve the perturbed time-varying linear system in [27], which suggests to us that RNN may be also useful in the control of the robotic systems. Lyu and Cheah [28] proposed a neural-network-based offline learning algorithm and an online learning controller to achieve the task-space tracking of robot manipulators with unknown kinematics and dynamics. Compared with the feed-forward neural networks employed in the above method, a novel recurrent neural network, termed as zeroing neural network (ZNN) [29],could be a better choice for the control of robotic arms since it is designed for time-varying problems and does not require the pre-training process. For example, Chen and Zhang [30]developed a Jacobian-matrix-adaption method to solve the tracking control problem of the PUMA 560 robot manipulator based on ZNN and achieved excellent results. An acceleration-level data-driven repetitive motion planning scheme for the kinematic control of robots with unknown structure was proposed in [31]. It is worth noting that the aforementioned schemes are conducted in ideal conditions or only consider random noise. However, there always exist different types of noise and external disturbances in the real world. As a result,this motivates us to develop a better noise-tolerant model-free scheme based on ZNN to solve the kinematic control problem of robotic arms. Moreover, achieving finite-time convergence is also important to the application of the control scheme[32]–[34].

In view of the advantages of ZNN, various modified versions of ZNN have been proposed and investigated to improve convergence and robustness [35]–[37]. Specifically, Guo and Zhang [9] presented the application of ZNN activated by the Li-function to kinematic control of redundant robots. Xiaoet al. [38] employed two nonlinear activated ZNNs with finite-time convergence for solving time-varying linear matrix equations. To cope with noise, there are also a lot of modified ZNN models with noise-tolerant capabilities that have been developed [39]–[42]. For instance, Tanet al. [43] proposed a varying-parameter ZNN model with finite-time convergence and noise suppression capabilities for time-varying matrix Moore-Penrose inversion and applied the model to robot control. Xiaoet al. [44] studied a new ZNN with noise-tolerant capability using a versatile activation function (VAF) to solve time-dependent matrix inversion. Nevertheless, existing ZNNbased works focus on improving the performance of modelbased control of robotic arms. To the best of the authors’knowledge, the work on noise-tolerant ZNN models for the control of robotic arms with unknown models is still missing.

In this paper, we propose a integration-enhanced noise-tolerant ZNN (IENT-ZNN) model and a dual IENT-ZNN scheme for the kinematic control of robotic arms with unknown models. The originality of this work lies in the following aspects. Firstly, existing noise-tolerant ZNNs can only deal with specific noises while the proposed IENT-ZNN can handle more types of noises. Besides, existing noise-tolerant ZNNs are only applied to the model-based control of rigidlink robotic arms, which relies on the robot model. The proposed dual IENT-ZNN scheme is dedicated to achieving the noise-tolerant control of robotic arms with an unknown robot model. More importantly, different from existing control methods that are only designed for rigid-link robotic arms or continuum robotic arms, we propose a unified control method that is applicable to both rigid-link and continuum robotic arms. In addition, to the best of the authors’ knowledge, noise disturbance is not considered in most existing control methods for continuum robots while this paper makes a breakthrough toward the robust control of continuum robots. The main contributions of this paper are listed as follows.

1) A new IENT-ZNN model is designed by exploiting nonlinear activation functions and integration operation, which is critical to ensure the convergence and robustness of the proposed control system.

2) For the first time, a unified dual IENT-ZNN control scheme is proposed for the model-free tracking control of both the rigid-link robotic arm and the continuum robotic arm, by integrating two IENT-ZNNs. One of the two IENT-ZNNs is employed to generate the actuation signal for robotic arms and the other is used to estimate the Jacobian matrix of robotic arms.

3) The proposed scheme can achieve tracking control of robotic arms by relying on the user-defined input and the feedback information, without knowing the kinematics of the robotic arms. The finite-time convergence and noise-tolerant capability of the proposed control scheme are rigorously proven by theoretical analysis.

4) A cable-driven continuum robotic arm is fabricated to validate the proposed control scheme. This is the first time that noise-tolerant ZNN is applied to the control of a continuum robot prototype. Extensive simulations and experiments based on the rigid-link robotic arm and the continuum robotic arm are performed to show the feasibility and advantages of the proposed control scheme.

The remainder of this paper is organized as follows. In Section II, the IENT-ZNN scheme is proposed to improve the robustness of ZNN models. In Section III, a dual ZNNs scheme based on the proposed IENT-ZNN model is presented for the control of robotic arms with unknown models. The finite-time convergence and robustness of the proposed scheme are analyzed in Section IV. In Section V, verification based on continuum robotic arms is performed to verify the feasibility, convergence and robustness of the proposed control system. In Section VI, verification based on rigid-link robotic arms is carried out to validate the proposed control system. Finally, some conclusions are drawn in Section VII.For convenience, some import notations used in this paper are summarized in Table I.

TABLE I THE DESCRIPTION OF SOME IMPORTANT NOTATIONS

II. IENT-ZNN MODEL

In this section, the IENT-ZNN model is proposed for the robust control of robotic arms. The detailed design process is as follows.

For a dynamic system withz(t) denoting the actual state of the system andz*(t) denoting the desired state, according to the design method of ZNN [29], an indefinite error function is first defined as follows:

Then, the following formula is chosen as the time derivative of the error function to force the error globally and exponentially to converge to zero:

where β ＞0 is the design parameter of the ZNN model (2) to adjust the convergence rate of the neural network and θ(·) is the activation function. Finally, substituting the error function into (2) and solving the differential equation will lead to the solution to the problem to be solved.

For the original ZNN, a linear activation function (LAF)θ(x)=xis employed. To improve the performance of ZNN,various nonlinear activation functions have been proposed and investigated since different activation functions for ZNN will lead to different stability and convergence. For example, the combined activation function (CAF-ZNN) [45] and integration-enhanced linear activation function (IE-ZNN) [46] are exploited to improve the robustness of ZNN under the disturbance of noise. A versatile activation function (VAF-ZNN) is proposed to achieve finite-time convergence and to decrease the impact of noise in [38]. However, the solution error of CAF-ZNN and VAF-ZNN cannot converge to zero when disturbed by constant noise while the IE-ZNN performs poorly in the presence of random noise. To overcome these drawbacks,the following integration-enhanced noise-tolerant activation function is proposed for the ZNN model (IENT-ZNN):

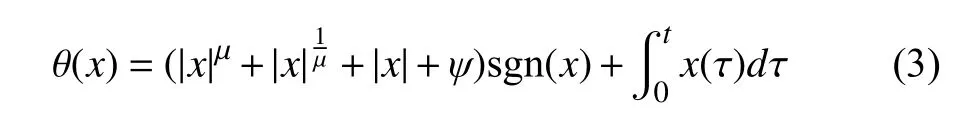
wherexis a time-varying variable, μ ∈(0,1) is a design parameter, |·| d enotes the absolute value of a scalar,ψ＞0 is a constant parameter, and sgn(·) is the sign function. The comparisons and formulations of these commonly used ZNN models are summarized in Table II. The proposed IENT-ZNN model plays an important role in ensuring the finite-time convergence and noise-suppressing capability of the control algorithm. It can deal with more kinds of noises than the existing ZNN models.

TABLE II COMPARISONS AND FORMULATIONS OF DIFFERENT ZNN MODELS

III. DUAL IENT-ZNN FOR TRACKING CONTROL

In this section, we describe the development of a unified control algorithm for both the rigid-link robotic arm and the continuum robotic arm without knowing the structure or parameters of the robotic arms.

A. Kinematics

Typically, the following equation is used to characterize the kinematics of robotic arms:

B. IENT-ZNN-Based Control Scheme

Tracking control, aimed at finding required actuator signals to control the end-effector of robotic arms to move along the desired path in the task space, is one of the most basic and important problems in robotics.

With the above knowledge, we next employ the proposed IENT-ZNN to solve the tracking control problem. First of all,to monitor the tracking process, a vector-valued indefinite error function is defined as follows:

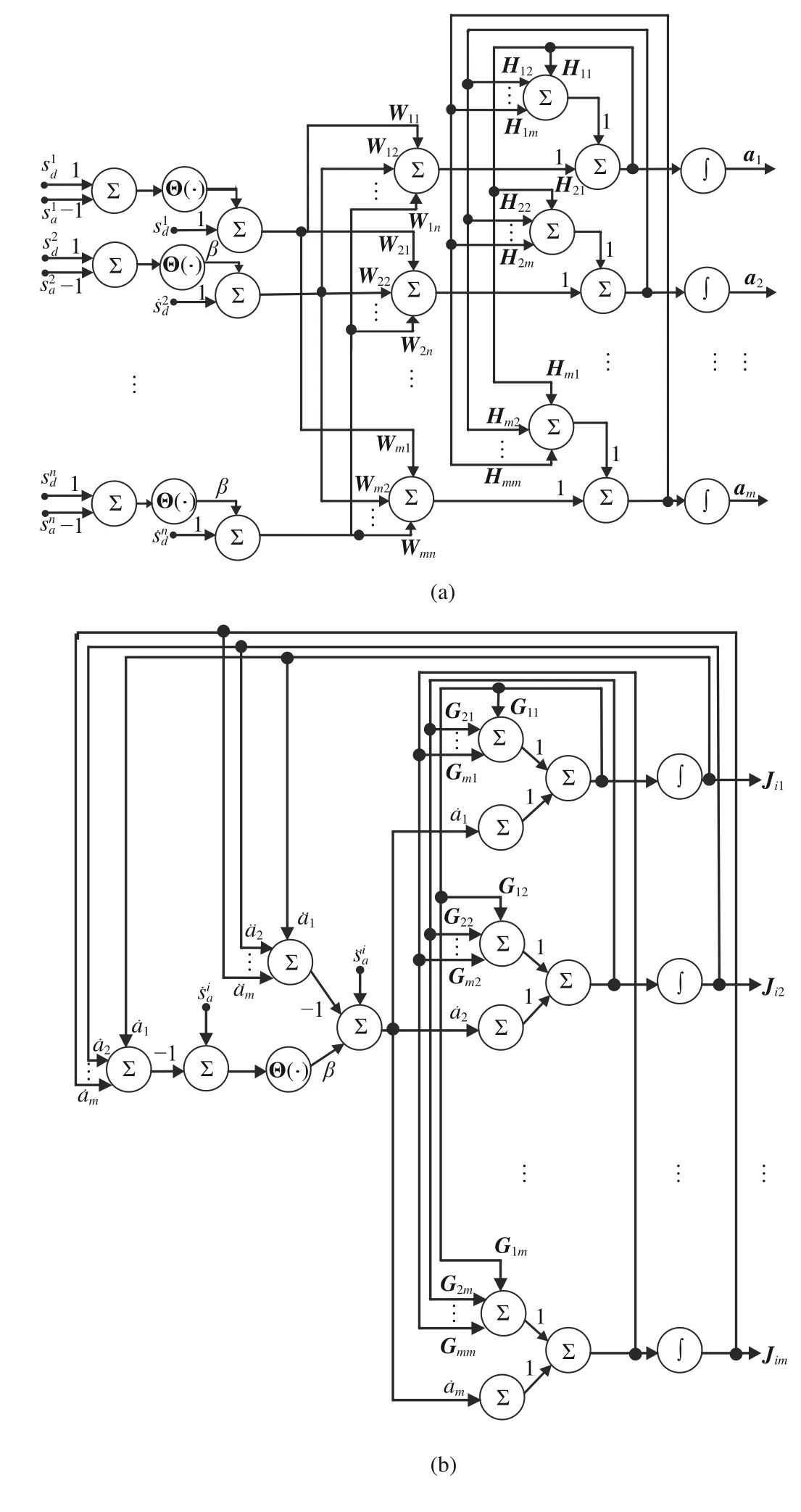
Fig. 1. Neural network structure diagram. (a) IENT-ZNN1; (b) IENTZNN2.

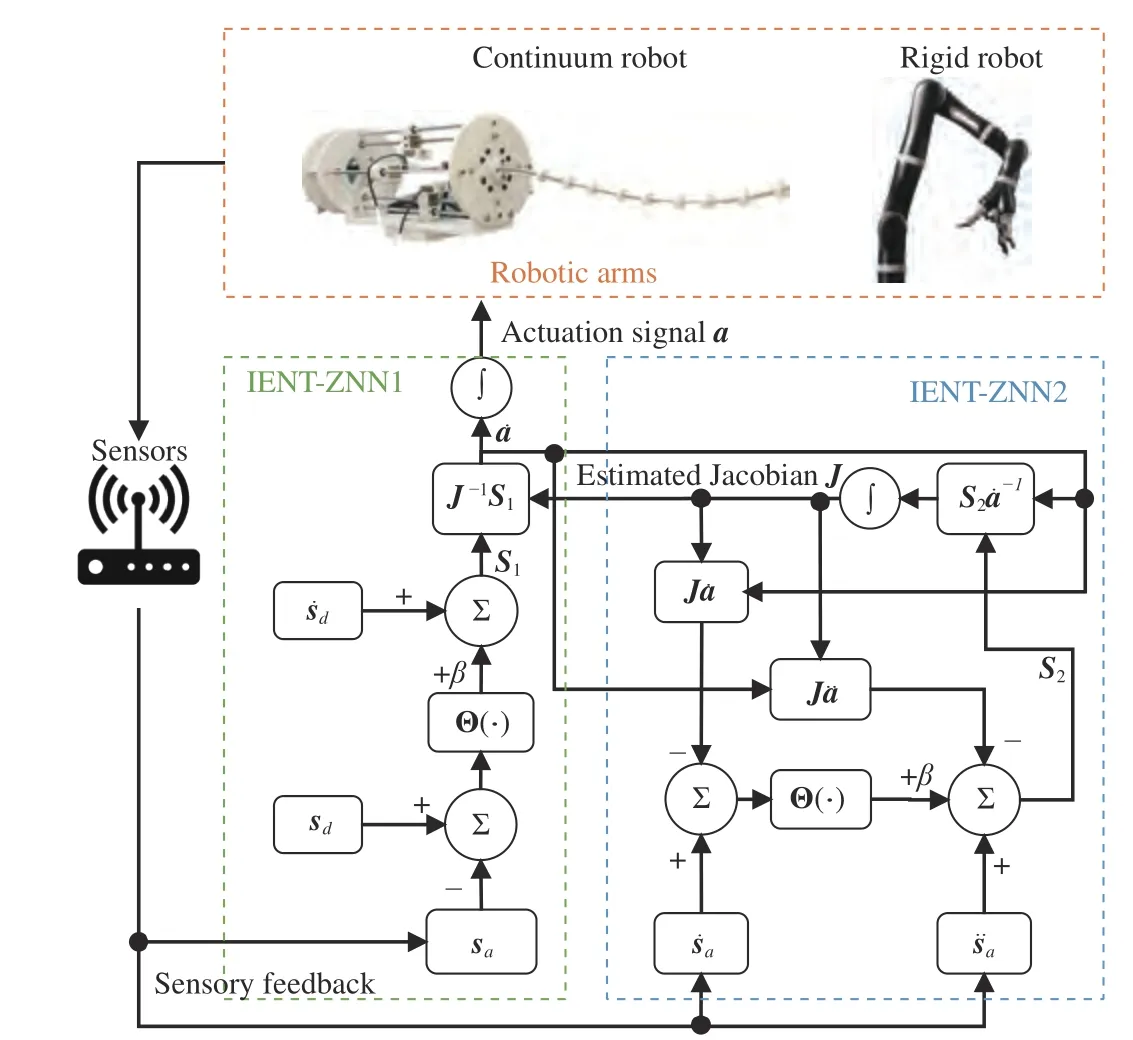
Fig. 2. Architecture of the control system for robotic arms based on dual IENT-ZNN.

Remark 2:The algorithm innovations of this paper can be summarized as the following facts. To begin, model-free control is a new trend for motion control of robotic arms, and our dual IENT-ZNN control algorithm is proposed to solve the noise-tolerant control for robotic arms in the condition that the kinematic model is not known. This is the first of its kind in the sense that previous noise-tolerant algorithms are all for model-based control, whereas our algorithm is model-free.Besides, ZNN-based control technologies applied to continuum robots are still in the primary stage (only two relevant works have been reported as we know, and neither of them has conducted experimental verification), and our algorithm is the one adopting totally new methodology and shows superior performance. Finally, to the best of the authors’ knowledge, this is the first unified control algorithm that is designed for and validated on both the rigid-link robotic arm and the continuum robotic arm.

IV. THEORETICAL ANALySIS

In this section, the convergence and robustness of the proposed tracking control method will be analyzed systematically under different conditions.

A. Noise-Free

In this part, we will analyze the finite-time convergence of the proposed control system in the absence of noise by the following theorem.

B. Noise-Polluted

When disturbed by noise, the IENT-ZNN1 model (7) is rewritten as

V. VERIFICATION BASED ON CONTINUUM ROBOTIC ARMS

In this section, simulations and experiments based on continuum robotic arms are performed to verify the feasibility and robustness of the proposed IENT-ZNN model and control system for solving the tracking control problem.

A. Simulations Based on the Continuum Robot

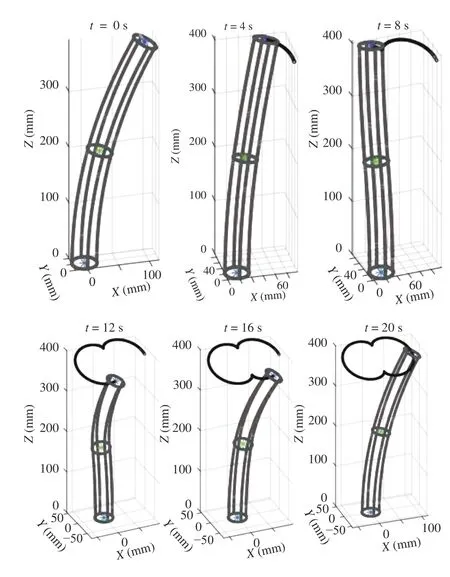
Fig. 3. Trajectory tracking process of the continuum robotic arm for tracking the double arc cycloid path.

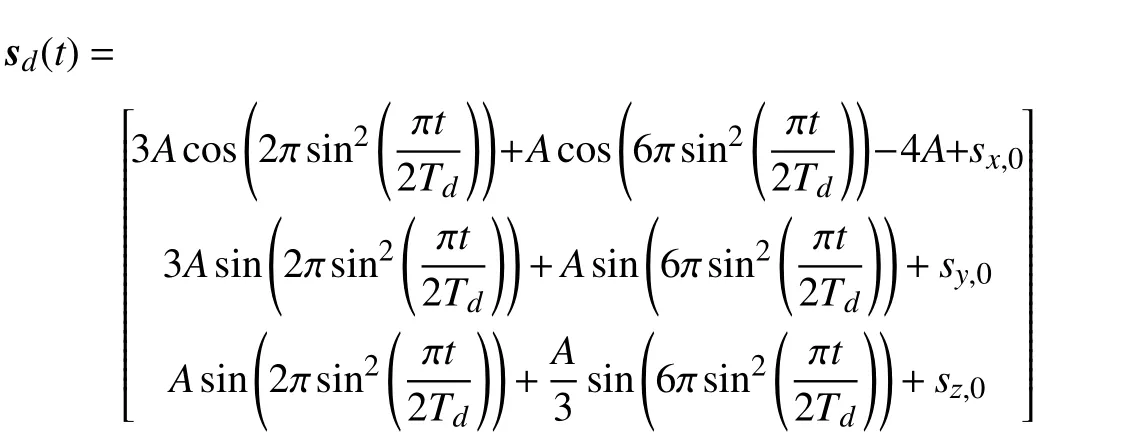
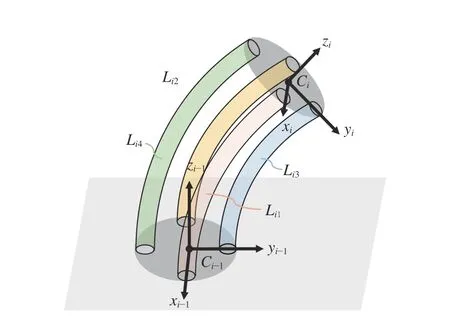
Fig. 4. The structure of the i-th segment of the continuum robotic arm.

whereA=20 mm is a constant to scale the desired path and[sx,0;sy,0;sz,0]is the absolute position of the desired path in the task space, i.e., the initial position of the end-effector. Firstly,we do not consider noise to verify if it is feasible to control the continuum robotic arm with the proposed control system.Fig. 3 illustrates some configurations of the continuum robotic arm at different time instants during the path tracking process.To demonstrate the convergence of the system, there are initial errors between the end-effector and the desired path. As can be seen in Fig. 5(a), the errors corresponding to different axes decrease rapidly and the root mean squared error(RMSE) is 0.1224 mm, where the RMSE is defined as

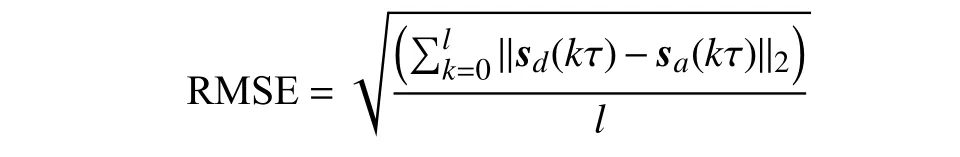
with τ=0.1 s being the sampling interval andl=Td/τ.Besides, based on the theoretical analysis, the convergence time should satisfytmax＜0.27 s. From Fig. 5(a), one can find that the tracking errors almost converge to zero att=0.1 s,which verifies the finite-time convergence of the proposed control system. In addition, the changes of configuration parameters during the task execution are illustrated in Fig. 5(b).

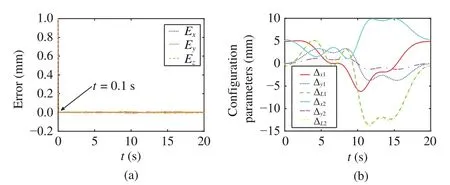
Fig. 5. Trajectory tracking results of the double arc cycloid path without noise when using the proposed control system. (a) Position errors of the endeffector corresponding to different coordinate axes; (b) The changes of configuration parameters.

2) Path Tracking:In this part, we steer the end-effector of the continuum robotic arm to move along a double arc cycloid path in the three-dimensional task space defined as follows:

3) Robustness and Comparisons:Despite the satisfactory performance of the proposed control system in the noise-free case, we are more concerned about the robustness of the control system based on the proposed IENT-ZNN compared with other ZNN schemes referred in Table II. The two norm of tracking errors, i.e., ‖e(t)‖2, is adopted to evaluate the performance of different models. Comparisons on tracking errors(i.e., ‖e(t)‖2) when employing different ZNN models under the disturbance of different type of noises are depicted in Fig. 6.Firstly, as shown in Fig. 6(a), the proposed control system can achieve superior convergence and sufficient small errors when employing these ZNN models except for LAF-ZNN and IEZNN in the noise-free case. When the control system is disturbed by constant noise (η (t)=5) as depicted in Fig. 6(b), the VAF-ZNN and the proposed IENT-ZNN have noise suppression capability since the errors almost converge to zero att=0.21s. When the IE-ZNN model is employed, one can find that the noise can also be suppressed to some extent. However, LAF-ZNN and CAF-ZNN both behave badly since the errors do not show a tendency to converge. When the control system is disturbed by linear time-varying noise η(t)=5t/Td,we can obtain similar results as illustrated in Fig. 6(c). Finally,the random noise is also considered in our simulations as shown in Fig. 6(d). We can easily find that the proposed IENT-ZNN model also achieves the best performance compared with other ZNN models. In this case, it is worth noting that the IE-ZNN model has bad performance, which means this model is not suitable for the case with random noise. In general, when employing the conventional LAF-ZNN and CAF-ZNN, the proposed control system has no noise suppression capability. The IE-ZNN has a certain effect on constant noise suppression and linear time-varying noise suppression but it is not suitable for the case with random noise. However,we can find that the tracking errors almost converge to zero in finite time under the disturbance of different noises when the proposed IENT-ZNN is adopted, which substantiates the robustness and efficacy of the proposed IENT-ZNN model and the proposed control system. It is also worth noting that the VAF-ZNN performs similarly to the proposed IENT-ZNN.To demonstrate the merits of the proposed IENT-ZNN, we increase the amplitude of noise (η (t)=10) and find that the tracking error also does not show a tendency to converge when the VAF-ZNN model is adopted, as depicted in Fig. 7.Comparatively, the tracking error still converges to zero gradually when the proposed IENT-ZNN is adopted in virtue of the integration operation in the model. The impact of parameter setting (i.e., the value ofβ) on the system is also worth studying. Theoretically, the value ofβmainly influences the convergence time of the control system, which is displayed in Table III. Obviously, the convergence time decreases as the parameterβincreases when the control system is disturbed by different noises. In order to further reveal the superiority of the proposed control system based on IENT-ZNN, we take the Kalman-filter-based (KF) and quadratic-programming-based(QP) model-free control methods as comparisons [15], [21].The numerical results in terms of RMSE of these methods are summarized in Table IV. Despite the acceptable errors of the KF method and the QP method in the noise-free case, one can easily find that the errors increase significantly when disturbed by noise. However, additive noise has a slight influence on the proposed IENT-ZNN-based method which illustrates the robustness and merits of the proposed control system for robot manipulators.

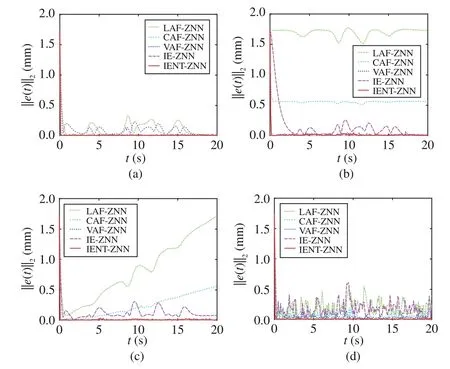
Fig. 6. Comparisons on two norms of tracking errors (i.e., ‖ e(t)‖2) based on the continuum robotic arm when employing different ZNN models under the disturbance of different type of noises. (a) Noise-free; (b) Disturbed by constant noise η (t)=5; (c) Disturbed by linear time-varying noise η (t)=5t/Td; (d)Disturbed by bounded random noise.

B. Experiments Based on the Continuum Robotic Arm

In this part, experiments based on a cable-driven continuum robot are performed to verify the effectiveness and noise-tolerant capability of the proposed IENT-ZNN-based control system. The experimental platform is shown in Fig. 8. The continuum robot is driven by four cables dragged by motors and there is also an extra motor at the base to control the translation of the robot. We use the Micron Tracker H3-60 visual camera to measure the actual position of the robot with the help of a marker attached to the end-effector.

Remark 4:Note that the proposed control system also demands other sensory feedback, namely the velocity and acceleration of the end-effector, to adapt the Jacobian matrix.The issue is that the velocity and acceleration may be difficultto be measured in practice. Inspired by [47] and [48], we define two low-pass filters to estimate the velocity and acceleration of the end-effector. The downside of this practice is that it may degrade the accuracy of the estimated Jacobian matrix. Fortunately, according to [49], the Jacobian matrix can be treated as a constant in a local region, which means slight error in the Jacobian matrix will not significantly influence the performance of the control system.

TABLE IV COMPARISONS ON RMSE SyNTHESIzED By DIFFERENT CONTROL SySTEM UNDER THE DISTURBANCE OF DIFFERENT NOISE. THE UNIT OF THE DATA IS MILLIMETER (MM)

Fig. 8. The platform of the continuum robot and related facilities.

Fig. 9. Some snapshots of the continuum robot for tracking the star path.(a) t =Td/4; (b) t =Td/2; (c) t =3Td/4; (d) t =Td.

1) Settings:The continuum robot is required to track a star path in the task space with the task duration being 150 s. The robot is actuated by five motors which meansm=5 and the initial state of these motors is deemed asa(0)=[0;0;0;0;0]rad. The parameters of the proposed activation function are set to be μ=0.6 andψ=2. The control system and the motor controller are deployed by Simulink in MATLAB2020a,which enables us to control the robot in real-time with the time sampling gap being 0.1 s.

2) Results:Some snapshots of the continuum robot tracking the star path in the absence of noise are depicted in Fig. 9,with the actual trajectory displayed in the pictures. The specific experiment results are illustrated in Fig. 10. One can find that the actual trajectory of the end-effector almost coincides with the desired path and the RMSE of the tracking error is 1.12 mm. These experimental results imply that the proposed IENT-ZNN-based control system is feasible for the control of the continuum robot. It is worth noting that the tracking error cannot converge to zero exactly in experiments as a result of the imperfect controllability of the motors and the measurement error (0.2 mm for a static object) of the visual sensor.Furthermore, we also want to validate the noise-tolerant capability of the proposed control system and compare with existing model-free zeroing-dynamics-based (MFZD) method [50].The experiment results are summarized in Fig. 11 where the two norms of tracking errors (‖e(t)‖2) in different cases are illustrated. Firstly, one can find that, with the same parameter setting, the proposed IENT-ZNN-based control system can achieve lower tracking error than the MFZD method in the noise-free case, which reveals the accuracy of the proposed method. Besides, comparative experiments are performed in the presence of linear noise. One can find that the MFZD method has poor noise-tolerant capabilities since the tracking error increases significantly when disturbed by noise. In comparison, the noise has negligible influence on the proposed IENT-ZNN-based method, which reveals the superior noisetolerant capabilities of the proposed method. In summary,these experimental results have verified the effectiveness,accuracy and robustness of the proposed IENT-ZNN-based method for the control of the continuum robotic arm.

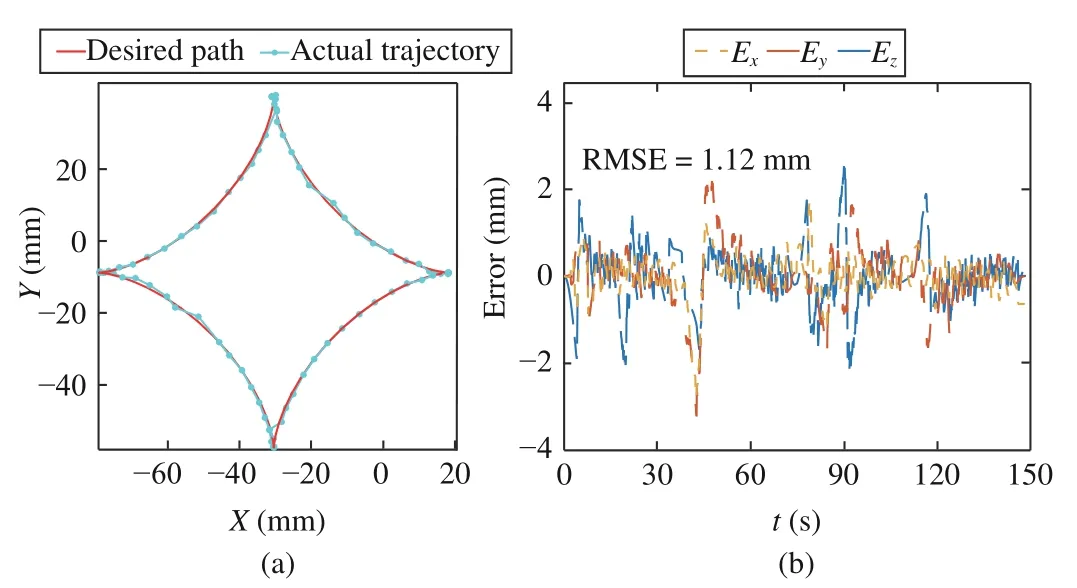
Fig. 10. Experiment results of the continuum robot for tracking the star path. (a) Profiles of the desired path and the actual trajectory of the robot; (b)Profiles of tracking errors corresponding to different axes.

Fig. 11. Comparisons on two norms of tracking errors (i.e., ‖e(t)‖2) based on the continuum robot when employing different methods under the disturbance of different type of noises.

VI. VERIFICATION BASED ON RIGID ROBOTIC ARMS

Fig. 12. The Jaco2 robotic arm and the host computer.

Fig. 13. Simulation results based on the Jaco2 manipulator when following an inner five ring pattern. (a) Tracking process of the Jaco2 robotic arm for tracking the inner five ring path; (b) Desired path and actual end-effector path; (c) The changes of joint angles.

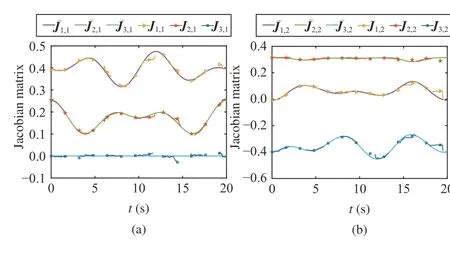
Fig. 14. Comparisons between the estimated Jacobian matrix J(t) and the actual Jacobian matrix J¯(t). (a) The first columns of the Jacobian matrices; (b) The second columns of the Jacobian matrices.

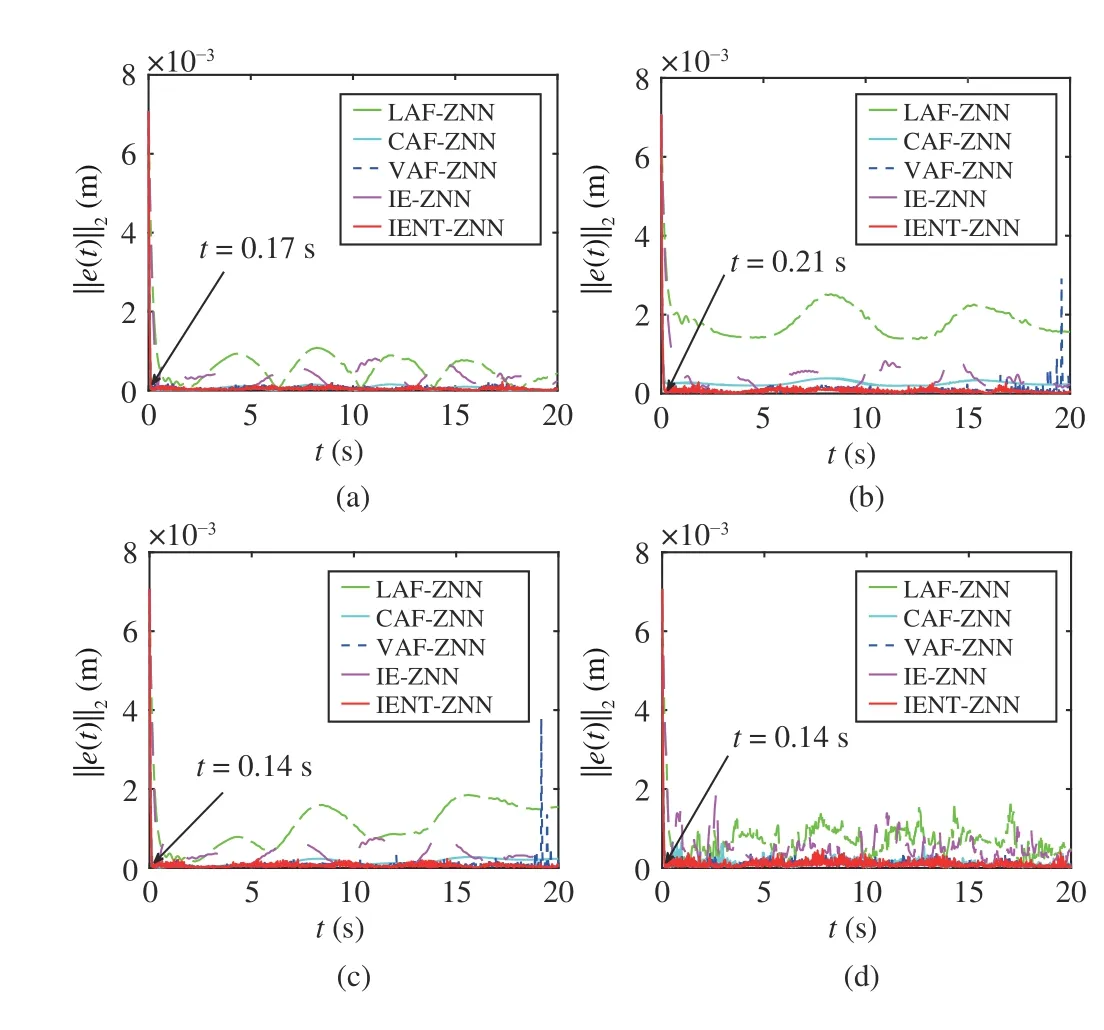
Fig. 15. Comparisons on two norms of tracking errors (i.e., ‖ e(t)‖2) based on the Jaco2 robotic arm when employing different ZNN models under the disturbance of different type of noises. (a) Noise-free; (b) Disturbed by constant noise η(t)=5×10-3; (c) Disturbed by linear time-varying noise η(t)=5t/Td×10-3; (d) Disturbed by bounded random noise.

Fig. 16. Some snapshots of the Jaco2 manipulator for drawing a pattern with the aid of the proposed IENT-ZNN in the absence of noise.

posed method also has the best performance, which verifies the superiority of the proposed IENT-ZNN scheme.

Fig. 17. Some snapshots of the Jaco2 manipulator for drawing a pentagram with aid of the proposed IENT-ZNN disturbed by linear time-varying noise η(t)=5t/Td×10-2.

Fig. 18. Some configurations of the Jaco2 manipulator for drawing a pentagram with aid of the IENT-ZNN disturbed by linear time-varying noise η(t)=5t/Td×10-2.

Remark 5:In this work, what we investigate is the proposed IENT-ZNN model and its application on the model-free tracking control of robotic arms without considering any constraint. However, there always exist actuation limits or obstacles in industrial applications. Therefore, determining how to construct a more comprehensive and practical control system is a problem worth studying in the future. For example, one can solve the inverse kinematics problem with quadratic programming, which takes secondary tasks into consideration,and estimate the Jacobian matrix with the IENT-ZNN model.

Fig. 19. Some snapshots of the Jaco2 manipulator for drawing a pentagram with aid of the VAF-ZNN disturbed by linear time-varying noiseη(t)=5t/Td×10-2.

Fig. 20. Some snapshots of the Jaco2 manipulator for drawing a pentagram in experiments with aid of the combined function activated RNN disturbed by linear time-varying noise η (t)=5t/Td×10-2.

VII. CONCLUSIONS

In this paper, firstly, an IENT-ZNN scheme is proposed to improve the convergence and robustness of ZNN models.Based on the proposed IENT-ZNN model, a noise-tolerant dual zeroing neural networks scheme is presented for the tracking control of robotic arms. Being comprised of two IENT-ZNN models, the proposed control system can solve the inverse kinematics problem without knowing the model information of robotic arms, which makes it easier to apply the proposed control system to different robotic arms. Theoretical analysis has revealed that the proposed control system has superior convergence and robustness. It is proven that the tracking error synthesized by the proposed control system can converge to zero in finite time even under the disturbance of bounded noise. Finally, extensive simulations and experiments based on continuum robots and rigid-link robotic arms have been performed to validate the proposed control method.The results have revealed the feasibility of the proposed control scheme. Compared to existing methods, the proposed scheme has achieved better accuracy and noise-tolerant capabilities.

It should be noted that this work investigates the kinematic position control of robotic arms without considering the force at the end-effector, which limits the application of the proposed method to tasks that do not require consideration of force, such as welding and painting. Therefore, developing a position/force hybrid control system for robotic arms will be part of our future work, which allows the robotic arm to better interact with its environment and perform more complex tasks.