趋近饱和定律在纳米永磁材料磁性研究中的应用

吕庆荣，黄靖雯，冯双久

(1. 安徽大学 物理与光电工程学院，2. 安徽大学 物质科学与信息技术研究院，3. 安徽大学 材料科学与工程学院，安徽 合肥 230601)

作为尖晶石铁氧体中的永磁材料，钴铁氧体除了具有较高矫顽力和饱和磁化强度，还具有高机械强度和良好的稳定性.钴铁氧体纳米颗粒在高密度磁记录、生物医药及磁性液体等许多领域有广泛的应用[1-3].饱和磁化强度Ms是磁性材料在外加磁场中被磁化时所能够达到的最大磁化强度，矫顽力Hc表征材料抵抗外部反向磁场或其它退磁效应的能力，它们都是衡量永磁材料磁性能的重要参数.磁晶各向异性是影响纳米永磁材料矫顽力的重要因素，研究磁晶各向异性对于探索矫顽力增强机理非常必要.

在强磁场区域，磁化已趋于饱和状态，此时多晶体的磁化曲线可以通过趋近饱和定律来描述.趋近饱和定律在实际应用中，可以用来精确测量材料的饱和磁化强度Ms和测量多晶材料的磁晶各向异性常数K1[4].本文用趋近饱和定律计算了纳米钴铁氧体样品在不同温度下的饱和磁化强度Ms和磁晶各向异性常数K1，并用磁晶各向异性常数随温度变化解释了材料在低温时的大矫顽力现象.

1 用趋近饱和定律分析饱和磁化强度随温度变化

用溶剂热法制备了颗粒尺寸约30 nm的CoFe2O4，用超导量子干涉仪振动样品磁强计(Quantum Design SQUID-VSM)测量了样品的磁化曲线和磁滞回线，磁化曲线与磁滞曲线是在零场降温后由一个程序同时测得的.图1为低温5 K 和室温300 K时的磁化曲线.可见，5 K时样品更难达到饱和磁化，用趋近饱和定律可以精确测定饱和磁化强度.

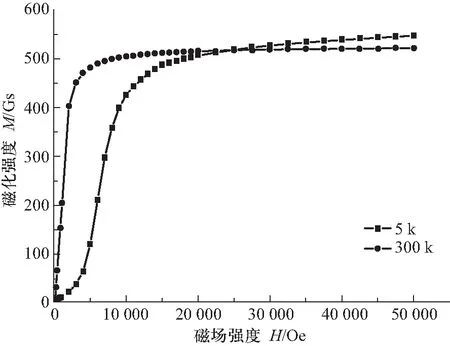
图1 样品在5 K和300 K时的磁化曲线

在强磁场区域，磁化已趋于饱和状态，此时多晶体的磁化曲线可以通过趋近饱和定律来描述，即

(1)

式中a为磁硬度系数，b为与磁化矢量转动过程有关的常数，χP为顺磁磁化率，χPH项为在极高磁场及高温下顺磁磁化过程对磁化强度的贡献，在此可以忽略.所以，上式可写为

(2)

在强磁场区域，H-2项可以忽略，则有

因为在强磁场区域，磁化强度趋于饱和，M≈Ms，所以

(3)

如图2所示，在强磁场区域，M/H～M有很好的线性关系，直线是Origin软件线性拟合结果.由图2(a)可知，低温5 K下的实验数据线性拟合的相关系数的平方R2=0.999，该直线在M轴的截距即为饱和磁化强度，Ms=5.76×102Gs.由图2(b)可知，室温300 K下的实验数据线性拟合的相关系数的平方R2=0.998，该直线在M轴的截距为Ms=5.28×102Gs.随着测量温度升高，饱和磁化强度Ms呈下降趋势.

磁性材料可以看作是单畴颗粒的集合体，在每一个单畴颗粒内，由于相邻电子之间有很强的交换作用，在没有外磁场时，自旋磁矩能“自发地”整齐排列起来，而且磁矩取向在由磁晶各向异性所决定的易磁化方向上，但是由于各颗粒的易磁化方向不同，磁矩的取向也就不同.当铁磁性材料处于外磁场中时，那些自发磁化方向和外磁场方向成小角度的磁畴，其体积随着外加磁场的增大而扩大，并使磁畴的磁化方向进一步转向外磁场方向.另一些自发磁化方向和外磁场方向成大角度的磁畴其体积则逐渐缩小，当外磁场进一步增大时，所有磁畴都沿外磁场排列好，介质的磁化就达到饱和.

随着温度升高，热扰动能增加，自旋取向的随机性增大，能够严格按照外磁场方向排列的自旋相应减少，使得饱和磁化强度降低[6].趋近饱和定律计算结果与理论分析结论一致.

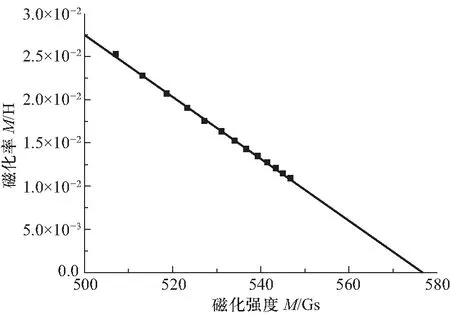
5 K

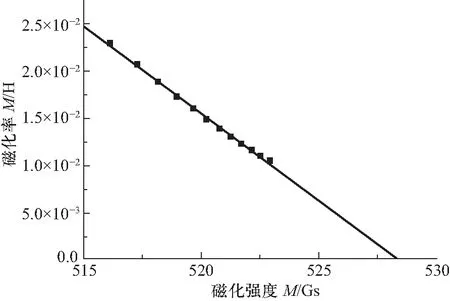
300 K图2 强磁场区M/H随M变化情况(方块为实验数据点，直线为线性拟合结果)

2 用趋近饱和定律分析矫顽力随温度变化

图3为样品在5 K 和300 K时的磁滞回线，左上角插图为磁滞回线在较小的磁场强度和磁化强度范围内的放大图.磁滞回线与H轴负向交点对应的磁场强度值即为矫顽力Hc，温度为5 K时，Hc=5.22×103Oe；300 K时，Hc=6.47×102Oe.低温时，材料具有很大矫顽力，随温度升高，矫顽力下降很快.

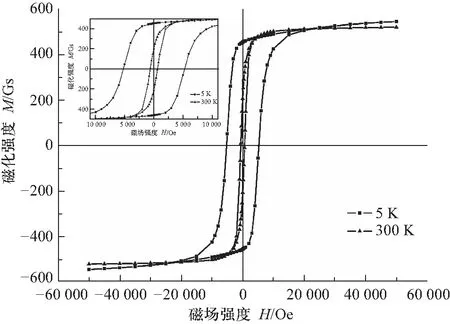
图3 样品在5 K 和300 K时的磁滞回线

系统被冷却到低温，热扰动能低，所以每个颗粒磁矩均分布在各自的易磁化方向.在施加一个很小的外磁场时，颗粒磁矩由于自旋“冻结”，并不能有效地向外磁场方向偏转，磁晶各向异性大，所以矫顽力很大.随着体系温度逐渐升高，热扰动能增加，被冻结的自旋磁距逐渐被外磁场影响，跨过能垒，向外场方向偏转，即自旋“解冻”，磁晶各向异性快速下降，室温时矫顽力迅速降低.所以，矫顽力随温度增加而快速下降的主要原因是磁晶各向异性随温度变化[7,8].

为了评估磁晶各向异性随温度变化情况，需要测定不同温度下的磁晶各向异性常数.趋近饱和定律中的系数b是来源于磁晶各向异性对较强磁场下畴转磁化的阻滞作用.根据磁性物质内的各种相互作用的能量，从理论上可以推导出系数b与磁晶各向异性常数K1的关系.对于立方晶系的多晶体，可以导出[5]

(4)

因此，已知系数b和饱和磁化强度Ms可以求得磁晶各向异性常数K1.将式(2)对H进行微分后，可得

在较强的磁场下，2b>>aH，则有

(5)

即，微分磁化率dM/dH与H-3的函数关系近似为过原点的直线，该直线的斜率为2bMs，已知Ms即可确定b值[4].

图4为较强磁场下微分磁化率dM/dH随H-3变化情况，直线为Origin软件线性拟合结果.由图4(a)可知，5 K时线性拟合相关系数平方R2=0.996，斜率2bMs=2.51×1010Oe3，将Ms=5.76×102Gs代入，得到b=2.18×107Oe3/Gs，再将b和Ms代入式(4)可求得K1=9.74×106erg/cm3.

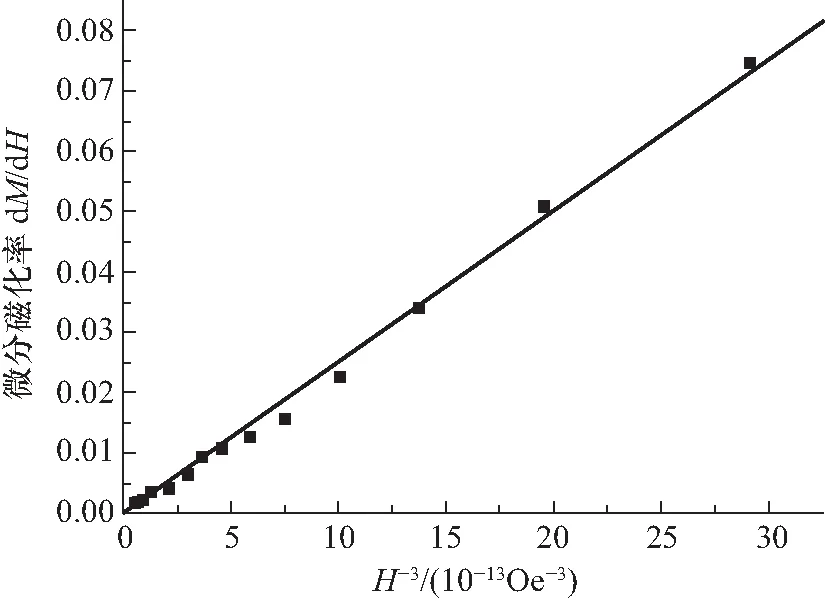
5 K

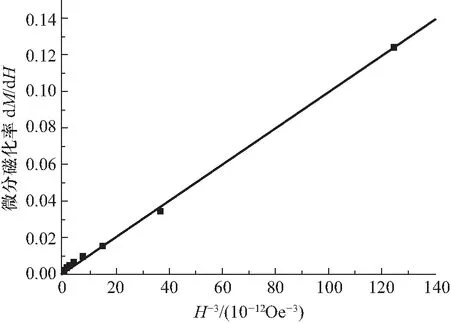
300 K图4 较强磁场下dM/dH随H-3变化情况(方块为实验数据点，直线为线性拟合结果)

由图4(b)可知，300 K时线性拟合相关系数平方R2=0.999，斜率2bMs=9.87×108Oe3，将Ms=5.28×102Gs代入，得到b=9.34×105Oe3/Gs,再将b和Ms代入式(4)可求得K1=1.85×106erg/cm3.

可见，低温5 K时，材料具有很大的磁晶各向异性常数，随温度上升，磁晶各向异性常数快速下降，与矫顽力随温度变化趋势一致.进一步证明磁晶各向异性是影响矫顽力的主要因素，提高磁晶各向异性是增大纳米永磁材料矫顽力的主要途径.

3 结论

用趋近饱和定律计算了纳米钴铁氧体样品在温度为5 K和300 K时的饱和磁化强度和磁晶各向异性常数.随着温度升高，热扰动能增加，使得饱和磁化强度降低，趋近饱和定律计算结果与理论分析结论一致.磁晶各向异性是影响矫顽力的主要因素，趋近饱和定律计算表明材料在5 K时具有很大的磁晶各向异性常数，随温度上升，磁晶各向异性常数快速下降，与矫顽力随温度变化趋势一致.