光杠杆法测杨氏模量实验的一种改进方法
2022-10-25荣振宇王晗语姜恒钧韩玉晶陈小艺
张 莉,荣振宇,王晗语,姜恒钧,韩玉晶,陈小艺
(济南大学 物理科学与技术学院,山东 济南 250022)
杨氏模量是反映固体材料抵抗弹性形变能力的物理量,它的测定在科学研究和技术应用中都具有重要意义.在大学物理实验中,杨氏模量的测量方法大致分为静态拉伸法和动态法两类.静态拉伸法是将被测金属丝拉伸后,通过对金属丝微小伸长量的测量实现杨氏模量的测量.实验中,金属丝的微小伸长量可以借助光杠杆[1]或激光杠杆[2,3]进行放大测量,也可以借助箔式应变片[4]、霍尔位置传感器[5]、位移光栅尺[6]等传感器进行测量,还可以利用莫尔条纹[7]、劈尖干涉[8]、数字激光散斑照相术[9]等光学手段实现测量.动态法则是通过对做受迫振动或自由阻尼振动[10]的被测材料的频率等参数进行测量,进而实现其杨氏模量的测量.静态拉伸法中的光杠杆法原理直观、简单,因此在大学物理实验教学中应用较多.
传统的光杠杆法测杨氏模量的实验中需要测量光杠杆平面镜到标尺的距离,且该距离一般要求一米以上,因此会导致测量的不便.本论文通过对传统的光杠杆法测杨氏模量的实验装置的改进,将原本光杠杆平面镜到标尺距离的测量,改为测量该距离的改变量,由此实现杨氏模量的测量.
1 光杠杆法测杨氏模量的改进
在弹性形变范围内,固体材料应力与应变的比值定义为杨氏模量.对于一条原长度为L0、横截面面积为S(直径为d)的金属丝,在拉力F的作用下发生了ΔL的微小伸长量,则其杨氏模量可以表示为
(1)
金属丝的微小伸长量ΔL采用光杠杆进行测量.如图1所示,设光杠杆两前足连线与后足的距离为b,光杠杆平面镜到标尺的距离为D0,则待测金属丝的微小伸长量ΔL可以近似表示为
(2)
其中,Δx为未施加拉力时与施加拉力F后标尺刻度的变化量.将式(2)代入式(1),可得
(3)
式(3)即传统光杠杆法测杨氏模量的计算公式.
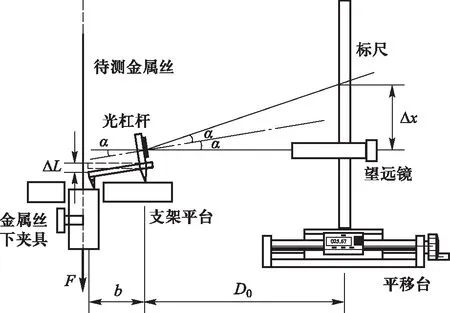
图1 改进后的光杠杆法测杨氏模量实验装置图
在传统的光杠杆法测杨氏模量实验中,往往取L0、d、b以及D04个物理量为恒定值,然后在增加或减小拉力F前后测量标尺刻度的变化量Δx.为了降低测量结果的相对不确定度,实验一般要求光杠杆平面镜到标尺的距离较大,但这样会导致D0值测量的不便.为了解决这一问题,本论文将传统杨氏模量实验仪的望远镜与标尺组合安装在一个带有读数装置的一维平移台上(如图1所示),平移台可以带动望远镜与标尺同步移动.实验中在金属丝所受拉力为某一定值且保持不变时,调节平移台移动望远镜和标尺组合,利用平移台的读数装置测量光杠杆平面镜到标尺距离的改变量ΔD,并通过望远镜测量平移台移动前后标尺刻度的改变量ΔX,以此替代传统实验方法中D0值和Δx值的测量.
2 改进后的光杠杆法测杨氏模量原理
改进后的光杠杆法测杨氏模量的原理图如图2所示.实验前先将一维平移台放在距离光杠杆大约1~2 m处,并按传统方法调节好光杠杆和望远镜,使得光杠杆平面镜为竖直状态;再调节平移台的移动方向,使之与此时光杠杆平面镜的法线方向保持一致;最后调节平移台,将望远镜与标尺组合移动到其可调范围内最接近光杠杆的位置附近.
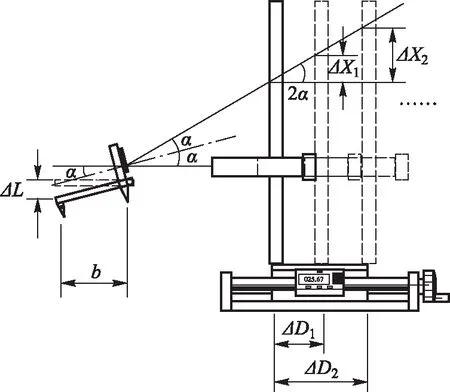
图2 改进后的光杠杆法测杨氏模量的原理图
当实验中施加给金属丝的拉力为F时,由于光杠杆平面镜的转动,镜面法线偏转到与水平方向夹角为α.首先,调节平移台将标尺向远离光杠杆的方向移动到标尺的某一刻度线与望远镜十字叉丝重合的位置,此时标尺的刻度值与平移台读数装置的示数分别作为标尺刻度的改变量ΔX与光杠杆平面镜到标尺距离的改变量ΔD的测量“零点”;再次调节平移台将标尺向远离光杠杆的方向移动,当标尺刻度的改变量ΔX1=1 mm时,记录光杠杆平面镜到标尺距离的改变量ΔD1;然后继续移动标尺,依次记录标尺刻度的改变量分别为ΔX2=2 mm,ΔX3=3 mm,…时光杠杆平面镜到标尺距离的改变量ΔD2、ΔD3、…;当平移台在其可调范围内由接近光杠杆的近端移动到其远端后,再反向移动平移台,在相同ΔX值的条件下再测量一组ΔD值;最后,将往返两次测量的ΔD值对应取平均值,再与相应的ΔX值进行线性拟合计算,即可计算出拉力为F的条件下光杠杆平面镜的反射光线的斜率k,且根据图2有
(4)
因此,由式(4)可以得出此时待测金属丝的微小伸长量ΔL可以近似表示为
(5)
再将式(5)代入式(1),可得杨氏模量的计算公式为
(6)
3 测量结果
图3是本论文改进后的实验装置实物图,该装置是在杭州光学电子仪器有限公司生产的HG-YMC-IV型杨氏模量测定仪的基础上加以改进,其数字拉力计的施力范围是0~20 kg,分辨率为0.01 kg,其标尺的刻度范围是-15~15 cm,最小刻度为1 mm;平移台使用的是北京大恒光电生产的GCM-830303M型手动数显平移台,其移动行程为100 mm,分辨率为0.01 mm.实验中分别利用卷尺(极限误差为0.5 mm)、螺旋测微器(极限误差为0.004 mm)和游标卡尺(极限误差为0.02 mm)测量实验用钢丝的长度L0、直径d以及光杠杆两前足连线与后足的距离b,实验数据及其处理结果如表1-3所示.

实验装置整体图

改进后的望远镜与标尺组合实物图图3 改进后的实验装置实物图
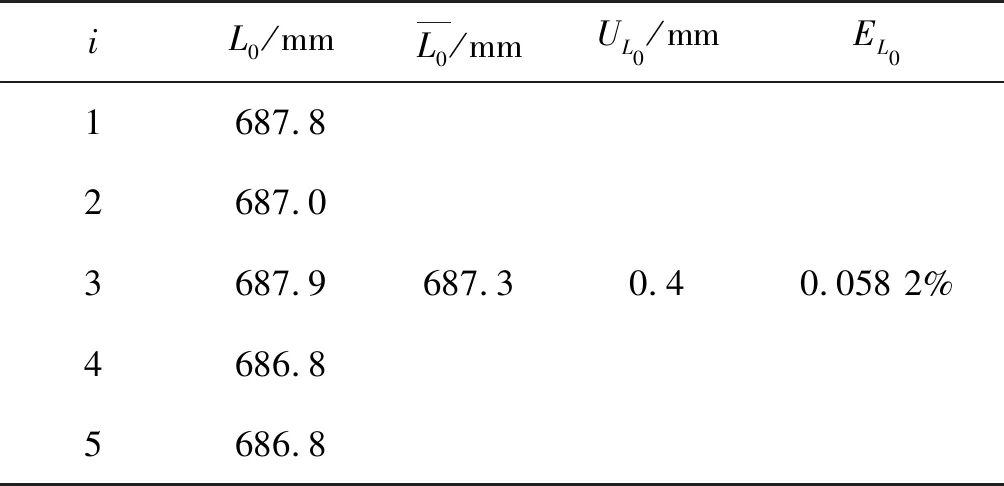
表1 钢丝长度的数据处理
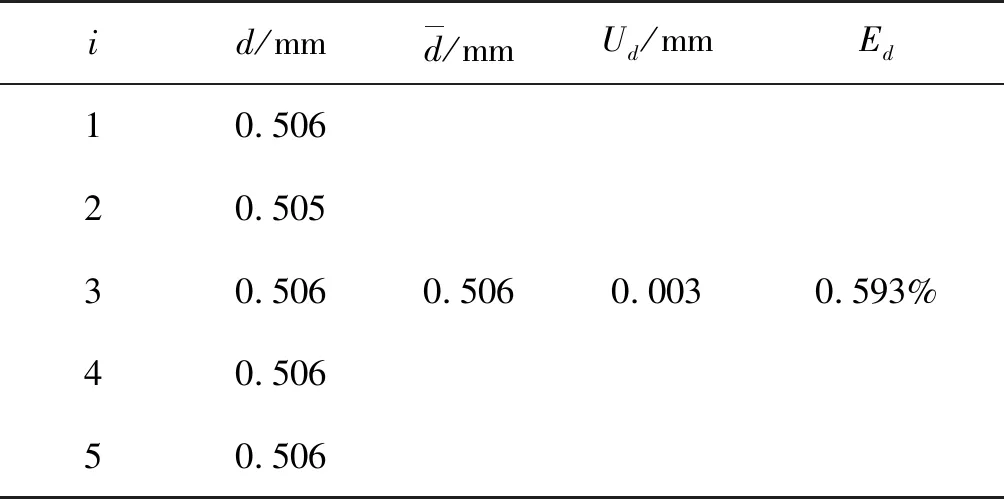
表2 钢丝直径的数据处理
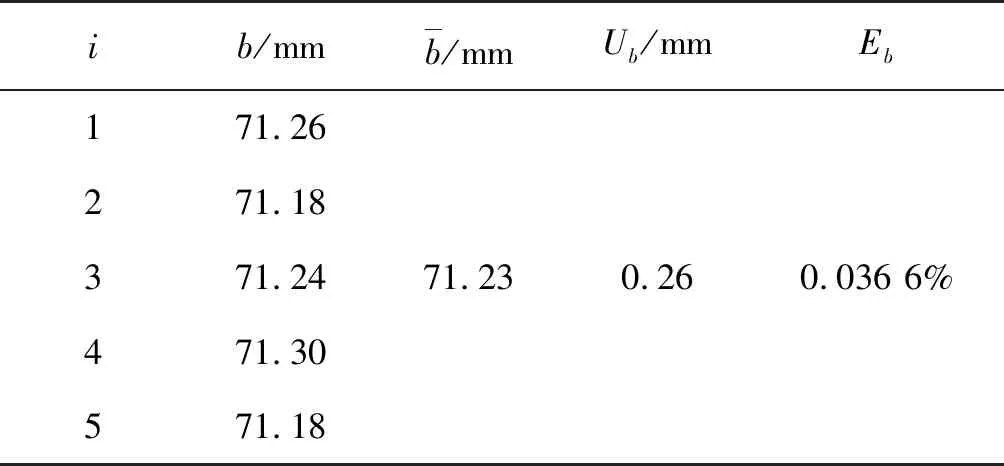
表3 光杠杆两前足连线与后足距离的数据处理
为了减小钢丝弯曲、钢丝夹具卡口摩擦力、弹性滞后等因素的影响,实验测量中一是需要在实验之初对钢丝施加一定的初始拉力以预拉伸钢丝,二是所施加的拉力采用先增加后减小的方式进行两组测量.此外,结合本论文所采用的测量原理,还需要在拉力为某一定值且保持不变的情况下,调节平移台进行往返两组测量以降低测量的随机误差.
在实验过程中,施力系统在施加3.00 kg砝码相应的预拉力的基础上,每次增加1.00 kg砝码相应的拉力直至13.00 kg砝码相应的拉力,之后每次再减小1.00 kg砝码相应的拉力直至3.00 kg砝码相应的拉力;在拉力为某一定值且保持不变的情况下,调节平移台往返两次测量在标尺刻度的改变量依次为1.0 mm、2.0 mm、3.0 mm、…时光杠杆平面镜到标尺距离的改变量,然后将标尺刻度的改变量与两次光杠杆平面镜到标尺距离改变量的平均值作线性拟合计算,得到增加拉力和减小拉力过程中各拉力值条件下反射光线的斜率如表4所示.
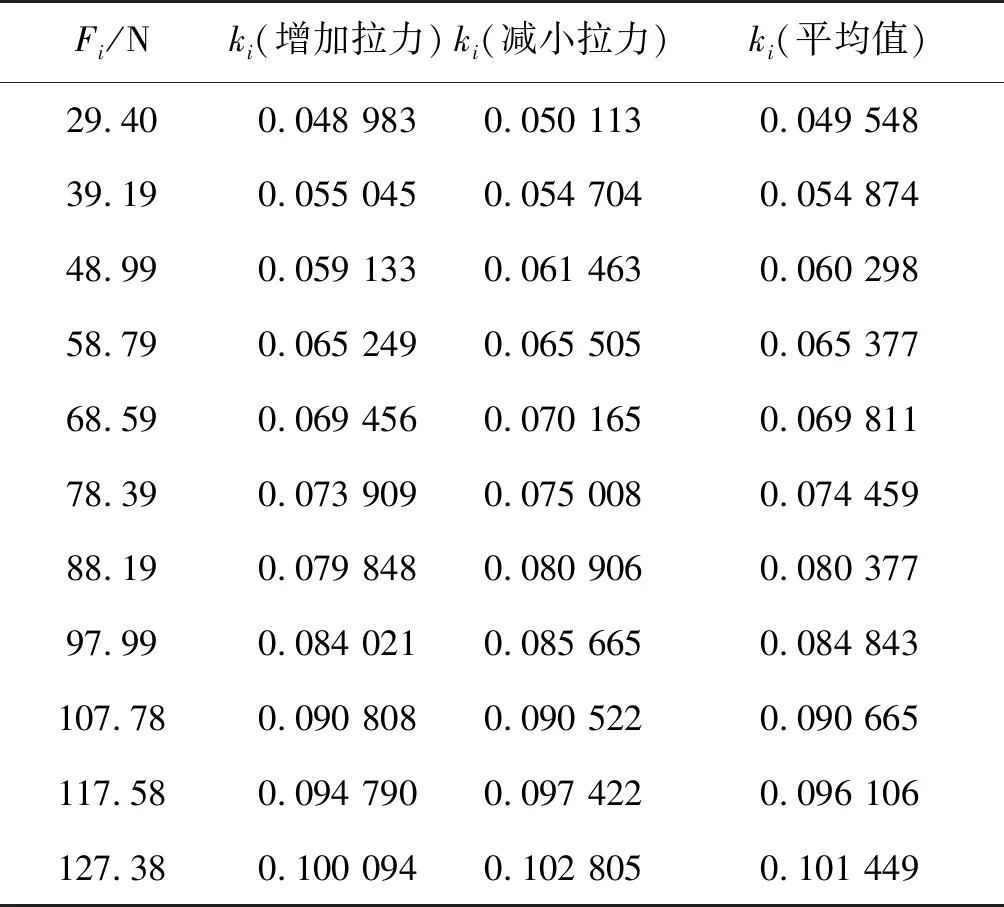
表4 砝码质量及其相应反射光线的斜率
在传统的光杠杆法测杨氏模量实验中,往往采用逐差法进行数据处理.因此,将利用逐差法得到的拉力变化量ΔF及与之相应的反射光线斜率的变化量Δk代入式(6),则杨氏模量的计算公式又可以
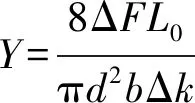
(7)
还可以将上述所测得的反射光线的斜率ki与相应的拉力Fi再次进行线性拟合计算,此时所得的斜率dk/dF即表示反射光线的斜率随拉力改变时的变化率.因此,式(7)又可以进一步写为
(8)
式(8)即为利用本论文改进后的光杠杆法测杨氏模量最终的计算公式.
利用表(4)所得数据,以拉力Fi为自变量,反射光线斜率的平均值ki为因变量进行线性拟合计算,最终计算所得反射光线的斜率随拉力的变化的斜率为dk/dF=(0.000 524 22±0.000 004 53) N-1.
将上述计算结果代入式(8),计算所测钢丝的杨氏模量的平均值为
其间接测量的相对不确定度为
则杨氏模量的总不确定度为
最终实验测得钢丝的杨氏模量为
EY=1.4%
4 结论
本论文在现有光杠杆法杨氏模量测定仪的基础上,在标尺处安装一个带有读数装置的平移台,一方面利用该装置测量光杠杆平面镜到标尺距离的改变量ΔD,从而解决传统方法中测量较大的距离D0所带来的不便,可以提高单人完成实验的便捷性;另一方面当金属丝受到的拉力为某一定值且保持不变时,传统的光杠杆法测杨氏模量实验仅对标尺刻度进行单次测量,而本论文通过调节平移台可以实现相同实验条件下的多次测量,从而可以降低测量中随机误差的影响.
